1. Background

Easter commemorates the resurrection of Jesus, which is believed to have occurred on the third day (inclusive) after Passover. In the Hebrew calendar, Passover occurs on the 14th of Nisan. Nisan is the first month of spring in the Northern Hemisphere, with the 14th corresponding to a full moon. Additionally, by the 2nd century, many Christians chose to only observe Easter on a Sunday.^{[1]:xxxv-xxxvii}

In order to separate the dating of Easter from the Hebrew calendar, it was necessary to identify the first full moon following the March equinox. By the time of the First Council of Nicaea, the Church of Alexandria had designated 21 March as an ecclesiastical date for the equinox, irrespective of actual astronomical observation. In 395, Theophilus published a table of future dates for Easter, validating the Alexandrian criteria.^{[1]:xxxviii-xl} Thereafter, the computus would be the procedure of determining the first Sunday after the first ecclesiastical full moon falling on or after 21 March.

2. History

The earliest known Roman tables were devised in 222 by Hippolytus of Rome based on eight-year cycles. Then 84 year tables were introduced in Rome by Augustalis near the end of the 3rd century.^[2]

Although a process based on the 19-year Metonic cycle was first proposed by Bishop Anatolius of Laodicea around 277, the concept did not fully take hold until the Alexandrian method became authoritative in the late 4th century.{{efn|The lunar cycle of Anatolius, according to the tables in De ratione paschali, included only two bissextile (leap) years every 19 years, so could not be used by anyone using the Julian calendar, which had four or five leap years per lunar cycle.^[3][4]

The Alexandrian computus was converted from the Alexandrian calendar into the Julian calendar in Rome by Dionysius Exiguus, though only for 95 years. Dionysius introduced the Christian Era (counting years from the Incarnation of Christ) when he published new Easter tables in 525.^[5][6]

A modified 84-year cycle was adopted in Rome during the first half of the 4th century. Victorius of Aquitaine tried to adapt the Alexandrian method to Roman rules in 457 in the form of a 532-year table, but he introduced serious errors.^[7] These Victorian tables were used in Gaul (now France) and Spain until they were displaced by Dionysian tables at the end of the 8th century.

The tables of Dionysius and Victorius conflicted with those traditionally used in the British Isles. The British tables used an 84-year cycle, but an error made the full moons fall progressively too early.^[8] The discrepancy led to a report that Queen Eanfled, on the Dionysian system – fasted on her Palm Sunday while her husband Oswy, king of Northumbria, feasted on his Easter Sunday.^[9]

As a result of the Irish Synod of Magh-Lene in 630, the southern Irish began to use the Dionysian tables,^[10] and the northern English Synod of Whitby in 664 adopted the Dionysian tables.^[11]

The Dionysian reckoning was fully described by Bede in 725.^{[1]:lix-lxiii} It may have been adopted by Charlemagne for the Frankish Church as early as 782 from Alcuin, a follower of Bede. The Dionysian/Bedan computus remained in use in western Europe until the Gregorian calendar reform, and remains in use in most Eastern Churches, including the vast majority of Eastern Orthodox Churches and Non-Chalcedonian Churches.^[12]

Having deviated from the Alexandrians during the 6th century, churches beyond the eastern frontier of the former Byzantine Empire, including the Assyrian Church of the East,^[13] now celebrate Easter on different dates from Eastern Orthodox Churches four times every 532 years.^[14]

Apart from these churches on the eastern fringes of the Roman empire, by the tenth century all had adopted the Alexandrian Easter, which still placed the vernal equinox on 21 March, although Bede had already noted its drift in 725 – it had drifted even further by the 16th century.^[15] Worse, the reckoned Moon that was used to compute Easter was fixed to the Julian year by the 19 year cycle. That approximation built up an error of one day every 310 years, so by the 16th century the lunar calendar was out of phase with the real Moon by four days. The Gregorian Easter has been used since 1583 by the Roman Catholic Church and was adopted by most Protestant churches between 1753 and 1845.

German Protestant states used an astronomical Easter between 1700 and 1776, based on the Rudolphine Tables of Johannes Kepler, which were in turn based on astronomical positions of the Sun and Moon observed by Tycho Brahe at his Uraniborg observatory on the island of Ven, while Sweden used it from 1739 to 1844. This astronomical Easter was the Sunday after the full moon instant that was after the vernal equinox instant using Uraniborg time (TT + 51^m). However, it was delayed one week if that Sunday was the Jewish date Nisan 15, the first day of Passover week, calculated according to modern Jewish methods. This Nisan 15 rule affected two Swedish years, 1778 and 1798, that instead of being one week before the Gregorian Easter were delayed one week so they were on the same Sunday as the Gregorian Easter. Germany's astronomical Easter was one week before the Gregorian Easter in 1724 and 1744.^[16] Sweden's astronomical Easter was one week before the Gregorian Easter in 1744, but one week after it in 1805, 1811, 1818, 1825, and 1829.^[17]

Two modern astronomical Easters were proposed but never used by any Church. The first was proposed as part of the Revised Julian calendar at a Synod in Constantinople in 1923 and the second was proposed by a 1997 World Council of Churches Consulation in Aleppo in 1997. Both used the same rule as the German and Swedish versions but used modern astronomical calculations and Jerusalem time (TT + 2^h 21^m) without the Nisan 15 rule. The 1923 version would have placed the astronomical Easter one month before the Gregorian Easter in 1924, 1943, and 1962, but one week after it in 1927, 1954, and 1967.^[18] The 1997 version would have placed the astronomical Easter on the same Sunday as the Gregorian Easter for 2000–2025 except for 2019, when it would have been one month earlier.^[19]

3. Theory

The Easter cycle groups days into lunar months, which are either 29 or 30 days long. There is an exception. The month ending in March normally has thirty days, but if 29 February of a leap year falls within it, it contains 31. As these groups are based on the lunar cycle, over the long term the average month in the lunar calendar is a very good approximation of the synodic month, which is 29.53059 days long.^[20] There are 12 synodic months in a lunar year, totaling either 354 or 355 days. The lunar year is about 11 days shorter than the calendar year, which is either 365 or 366 days long. These days by which the solar year exceeds the lunar year are called epacts (Greek: ἐπακταὶ ἡμέραι, translit. epaktai hēmerai, lit. 'intercalary days').^[21][22] It is necessary to add them to the day of the solar year to obtain the correct day in the lunar year. Whenever the epact reaches or exceeds 30, an extra intercalary month (or embolismic month) of 30 days must be inserted into the lunar calendar: then 30 must be subtracted from the epact. Charles Wheatly provides the detail:

"Thus beginning the year with March (for that was the ancient custom) they allowed thirty days for the moon [ending] in March, and twenty-nine for that [ending] in April; and thirty again for May, and twenty-nine for June &c. according to the old verses:

Impar luna pari, par fiet in impare mense;

In quo completur mensi lunatio detur.

"For the first, third, fifth, seventh, ninth, and eleventh months, which are called impares menses, or unequal months, have their moons according to computation of thirty days each, which are therefore called pares lunae, or equal moons: but the second, fourth, sixth, eighth, tenth, and twelfth months, which are called pares menses, or equal months, have their moons but twenty nine days each, which are called impares lunae, or unequal moons."^[23]

Thus the lunar month took the name of the Julian month in which it ended. The nineteen-year Metonic cycle assumes that 19 tropical years are as long as 235 synodic months. So after 19 years the lunations should fall the same way in the solar years, and the epacts should repeat. However, 19 × 11 = 209 ≡ 29 (mod 30), not 0 (mod 30); that is, 209 divided by 30 leaves a remainder of 29 instead of being a multiple of 30. So after 19 years, the epact must be corrected by one day for the cycle to repeat. This is the so-called saltus lunae ("leap of the moon"). The Julian calendar handles it by reducing the length of the lunar month that begins on 1 July in the last year of the cycle to 29 days. This makes three successive 29-day months.^[24] The saltus and the seven extra 30-day months were largely hidden by being located at the points where the Julian and lunar months begin at about the same time. The extra months commenced on 3 December (year 2), 2 September (year 5), 6 March (year 8), 4 December (year 10), 2 November (year 13), 2 August (year 16), and 5 March (year 19).^[1]:xlvi The sequence number of the year in the 19-year cycle is called the "golden number", and is given by the formula

GN = Y mod 19 + 1

That is, the remainder of the year number Y in the Christian era when divided by 19, plus one.^[25]

The paschal or Easter-month is the first one in the year to have its fourteenth day (its formal full moon) on or after 21 March. Easter is the Sunday after its 14th day (or, saying the same thing, the Sunday within its third week). The paschal lunar month always begins on a date in the 29-day period from 8 March to 5 April inclusive. Its fourteenth day, therefore, always falls on a date between 21 March and 18 April inclusive, and the following Sunday then necessarily falls on a date in the range 22 March to 25 April inclusive. In the solar calendar Easter is called a moveable feast since its date varies within a 35-day range. But in the lunar calendar, Easter is always the third Sunday in the paschal lunar month, and is no more "moveable" than any holiday that is fixed to a particular day of the week and week within a month.

4. Tabular Methods

4.1. Gregorian Calendar

As reforming the computus was the primary motivation for the introduction of the Gregorian calendar in 1582, a corresponding computus methodology was introduced alongside the calendar.^[26] The general method of working was given by Clavius in the Six Canons (1582), and a full explanation followed in his Explicatio (1603).

Easter Sunday is the Sunday following the paschal full moon date. The paschal full moon date is the ecclesiastical full moon date on or after 21 March. The Gregorian method derives paschal full moon dates by determining the epact for each year.^[27] The epact can have a value from * (0 or 30) to 29 days. Theoretically a lunar month (epact 0) begins with the new moon, and the crescent moon is first visible on the first day of the month (epact 1).^[28] The 14th day of the lunar month is considered the day of the full moon.^[29]

Historically the paschal full moon date for a year was found from its sequence number in the Metonic cycle, called the golden number, which cycle repeats the lunar phase 1 January every 19 years.^[30] This method was abandoned in the Gregorian reform because the tabular dates go out of sync with reality after about two centuries, but from the epact method, a simplified table can be constructed that has a validity of one to three centuries.^[31][32]

The epacts for the current Metonic cycle, which began in 2014, are:

Year	2014	2015	2016	2017	2018	2019	2020	2021	2022	2023	2024	2025	2026	2027	2028	2029	2030	2031	2032
Golden number	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
Epact[33]	29	10	21	2	13	24	5	16	27	8	19	*	11	22	3	14	25	6	17
Paschal full moon date[34]	14 April	3 April	23 March	11 April	31 March	18 April	8 April	28 March	16 April	5 April	25 March	13 April	2 April	22 March	10 April	30 March	17 April	7 April	27 March

The above table is valid from 1900 to 2199 inclusive. As an example of use, the golden number for 2038 is 6 (2038 ÷ 19 = 107 remainder 5, then +1 = 6). From the table, paschal full moon for golden number 6 is 18 April. From week table 18 April is Sunday. Easter Sunday is the following Sunday, 25 April.

The epacts are used to find the dates of the new moon in the following way: Write down a table of all 365 days of the year (the leap day is ignored). Then label all dates with a Roman numeral counting downwards, from "*" (0 or 30), "xxix" (29), down to "i" (1), starting from 1 January, and repeat this to the end of the year. However, in every second such period count only 29 days and label the date with xxv (25) also with xxiv (24). Treat the 13th period (last eleven days) as long, therefore, and assign the labels "xxv" and "xxiv" to sequential dates (26 and 27 December respectively). Finally, in addition, add the label "25" to the dates that have "xxv" in the 30-day periods; but in 29-day periods (which have "xxiv" together with "xxv") add the label "25" to the date with "xxvi". The distribution of the lengths of the months and the length of the epact cycles is such that each civil calendar month starts and ends with the same epact label, except for February and for the epact labels "xxv" and "25" in July and August. This table is called the calendarium. The ecclesiastical new moons for any year are those dates when the epact for the year is entered. If the epact for the year is for instance 27, then there is an ecclesiastical new moon on every date in that year that has the epact label "xxvii" (27).

Also label all the dates in the table with letters "A" to "G", starting from 1 January, and repeat to the end of the year. If, for instance, the first Sunday of the year is on 5 January, which has letter "E", then every date with the letter "E" is a Sunday that year. Then "E" is called the dominical letter for that year (from Latin: dies domini, day of the Lord). The dominical letter cycles backward one position every year. However, in leap years after 24 February the Sundays fall on the previous letter of the cycle, so leap years have two dominical letters: the first for before, the second for after the leap day.

In practice, for the purpose of calculating Easter, this need not be done for all 365 days of the year. For the epacts, March comes out exactly the same as January, so one need not calculate January or February. To also avoid the need to calculate the Dominical Letters for January and February, start with D for 1 March. You need the epacts only from 8 March to 5 April. This gives rise to the following table:

 

A table from Sweden to compute the date of Easter 1140–1671 according to the Julian calendar. Notice the runic writing. https://handwiki.org/wiki/index.php?curid=1226822

 

Chronological diagram of the date of Easter for 600 years, from the Gregorian calendar reform to the year 2200 (by Camille Flammarion, 1907). https://handwiki.org/wiki/index.php?curid=1338167

Label	March	DL	April	DL
*	1	D
xxix	2	E	1	G
xxviii	3	F	2	A
xxvii	4	G	3	B
xxvi	5	A	4	C
25	6	B
xxv			5	D
xxiv	7	C
xxiii	8	D	6	E
xxii	9	E	7	F
xxi	10	F	8	G
xx	11	G	9	A
xix	12	A	10	B
xviii	13	B	11	C
xvii	14	C	12	D
xvi	15	D	13	E
xv	16	E	14	F
xiv	17	F	15	G
xiii	18	G	16	A
xii	19	A	17	B
xi	20	B	18	C
x	21	C	19	D
ix	22	D	20	E
viii	23	E	21	F
vii	24	F	22	G
vi	25	G	23	A
v	26	A	24	B
iv	27	B	25	C
iii	28	C	26	D
ii	29	D	27	E
i	30	E	28	F
*	31	F	29	G
xxix			30	A

Example: If the epact is 27 (xxvii), an ecclesiastical new moon falls on every date labeled xxvii. The ecclesiastical full moon falls 13 days later. From the table above, this gives a new moon on 4 March and 3 April, and so a full moon on 17 March and 16 April.

Then Easter Day is the first Sunday after the first ecclesiastical full moon on or after 21 March. This definition uses "on or after 21 March" to avoid ambiguity with historic meaning of the word "after". In modern language, this phrase simply means "after 20 March". The definition of "on or after 21 March" is frequently incorrectly abbreviated to "after 21 March" in published and web-based articles, resulting in incorrect Easter dates.

In the example, this paschal full moon is on 16 April. If the dominical letter is E, then Easter day is on 20 April.

The label "25" (as distinct from "xxv") is used as follows: Within a Metonic cycle, years that are 11 years apart have epacts that differ by one day. A month beginning on a date having labels xxiv and xxv impacted together has either 29 or 30 days. If the epacts 24 and 25 both occur within one Metonic cycle, then the new (and full) moons would fall on the same dates for these two years. This is possible for the real moon^[35] but is inelegant in a schematic lunar calendar; the dates should repeat only after 19 years. To avoid this, in years that have epacts 25 and with a Golden Number larger than 11, the reckoned new moon falls on the date with the label 25 rather than xxv. Where the labels 25 and xxv are together, there is no problem since they are the same. This does not move the problem to the pair "25" and "xxvi", because the earliest epact 26 could appear would be in year 23 of the cycle, which lasts only 19 years: there is a saltus lunae in between that makes the new moons fall on separate dates.

The Gregorian calendar has a correction to the tropical year by dropping three leap days in 400 years (always in a century year). This is a correction to the length of the tropical year, but should have no effect on the Metonic relation between years and lunations. Therefore, the epact is compensated for this (partially – see epact) by subtracting one in these century years. This is the so-called solar correction or "solar equation" ("equation" being used in its medieval sense of "correction").

However, 19 uncorrected Julian years are a little longer than 235 lunations. The difference accumulates to one day in about 310 years. Therefore, in the Gregorian calendar, the epact gets corrected by adding 1 eight times in 2,500 (Gregorian) years, always in a century year: this is the so-called lunar correction (historically called "lunar equation"). The first one was applied in 1800, the next is in 2100, and will be applied every 300 years except for an interval of 400 years between 3900 and 4300, which starts a new cycle.

The solar and lunar corrections work in opposite directions, and in some century years (for example, 1800 and 2100) they cancel each other. The result is that the Gregorian lunar calendar uses an epact table that is valid for a period of from 100 to 300 years. The epact table listed above is valid for the period 1900 to 2199.

Details

This method of computation has several subtleties:

Every other lunar month has only 29 days, so one day must have two (of the 30) epact labels assigned to it. The reason for moving around the epact label "xxv/25" rather than any other seems to be the following: According to Dionysius (in his introductory letter to Petronius), the Nicene council, on the authority of Eusebius, established that the first month of the ecclesiastical lunar year (the paschal month) should start between 8 March and 5 April inclusive, and the 14th day fall between 21 March and 18 April inclusive, thus spanning a period of (only) 29 days. A new moon on 7 March, which has epact label "xxiv", has its 14th day (full moon) on 20 March, which is too early (not following 20 March). So years with an epact of "xxiv", if the lunar month beginning on 7 March had 30 days, would have their paschal new moon on 6 April, which is too late: The full moon would fall on 19 April, and Easter could be as late as 26 April. In the Julian calendar the latest date of Easter was 25 April, and the Gregorian reform maintained that limit. So the paschal full moon must fall no later than 18 April and the new moon on 5 April, which has epact label "xxv". 5 April must therefore have its double epact labels "xxiv" and "xxv". Then epact "xxv" must be treated differently, as explained in the paragraph above.

As a consequence, 19 April is the date on which Easter falls most frequently in the Gregorian calendar: In about 3.87% of the years. 22 March is the least frequent, with 0.48%.

 

Distribution of the date of Easter for the complete 5,700,000 year cycle. https://handwiki.org/wiki/index.php?curid=2068981

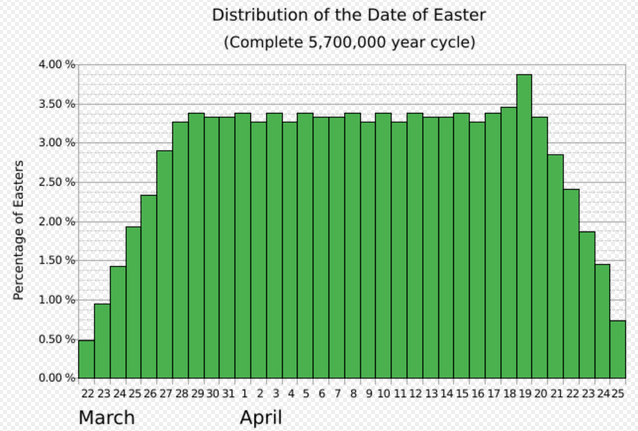
The relation between lunar and solar calendar dates is made independent of the leap day scheme for the solar year. Basically the Gregorian calendar still uses the Julian calendar with a leap day every four years, so a Metonic cycle of 19 years has 6,940 or 6,939 days with five or four leap days. Now the lunar cycle counts only 19 × 354 + 19 × 11 = 6,935 days. By not labeling and counting the leap day with an epact number, but having the next new moon fall on the same calendar date as without the leap day, the current lunation gets extended by a day,^[36] and the 235 lunations cover as many days as the 19 years. So the burden of synchronizing the calendar with the moon (intermediate-term accuracy) is shifted to the solar calendar, which may use any suitable intercalation scheme; all under the assumption that 19 solar years = 235 lunations (long-term inaccuracy). A consequence is that the reckoned age of the moon may be off by a day, and also that the lunations that contain the leap day may be 31 days long, which would never happen if the real moon were followed (short-term inaccuracies). This is the price for a regular fit to the solar calendar.

From the perspective of those who might wish to use the Gregorian Easter cycle as a calendar for the entire year, there are some flaws in the Gregorian lunar calendar^[37] (although they have no effect on the paschal month and the date of Easter):

1. Lunations of 31 (and sometimes 28) days occur.
2. If a year with Golden Number 19 happens to have epact 19, then the last ecclesiastical new moon falls on 2 December; the next would be due on 1 January. However, at the start of the new year, a saltus lunae increases the epact by another unit, and the new moon should have occurred on the previous day. So a new moon is missed. The calendarium of the Missale Romanum takes account of this by assigning epact label "19" instead of "xx" to 31 December of such a year, making that date the new moon. It happened every 19 years when the original Gregorian epact table was in effect (for the last time in 1690), and next happens in 8511.
3. If the epact of a year is 20, an ecclesiastical new moon falls on 31 December. If that year falls before a century year, then in most cases, a solar correction reduces the epact for the new year by one: The resulting epact "*" means that another ecclesiastical new moon is counted on 1 January. So, formally, a lunation of one day has passed. This next happens in 4199–4200.
4. Other borderline cases occur (much) later, and if the rules are followed strictly and these cases are not specially treated, they generate successive new moon dates that are 1, 28, 59, or (very rarely) 58 days apart.

A careful analysis shows that through the way they are used and corrected in the Gregorian calendar, the epacts are actually fractions of a lunation (1/30, also known as a tithi) and not full days. See epact for a discussion.

The solar and lunar corrections repeat after 4 × 25 = 100 centuries. In that period, the epact has changed by a total of −1 × 3/4 × 100 + 1 × 8/25 × 100 = −43 ≡ 17 mod 30. This is prime to the 30 possible epacts, so it takes 100 × 30 = 3,000 centuries before the epacts repeat; and 3,000 × 19 = 57,000 centuries before the epacts repeat at the same golden number. This period has 5,700,000/19 × 235 − 43/30 × 57,000/100 = 70,499,183 lunations. So the Gregorian Easter dates repeat in exactly the same order only after 5,700,000 years, 70,499,183 lunations, or 2,081,882,250 days; the mean lunation length is then 29.53058690 days. However, the calendar must already have been adjusted after some millennia because of changes in the length of the tropical year, the synodic month, and the day.

 

Graphs of the dates of Western (Catholic) and Eastern (Orthodox) Easter Sunday compared with the March equinox and full moons from 1950 to 2050 on the Gregorian calendar. https://handwiki.org/wiki/index.php?curid=1078836

This raises the question why the Gregorian lunar calendar has separate solar and lunar corrections, which sometimes cancel each other. Lilius's original work has not been preserved, but his proposal was described in the Compendium Novae Rationis Restituendi Kalendarium circulated in 1577, in which it is explained that the correction system he devised was to be a perfectly flexible tool in the hands of future calendar reformers, since the solar and lunar calendar could henceforth be corrected without mutual interference.^[38] An example of this flexibility was provided through an alternative intercalation sequence derived from Copernicus' theories, along with its corresponding epact corrections.^[39]

The "solar corrections" approximately undo the effect of the Gregorian modifications to the leap days of the solar calendar on the lunar calendar: they (partially) bring the epact cycle back to the original Metonic relation between the Julian year and lunar month. The inherent mismatch between sun and moon in this basic 19 year cycle is then corrected every three or four centuries by the "lunar correction" to the epacts. However, the epact corrections occur at the beginning of Gregorian centuries, not Julian centuries, and therefore the original Julian Metonic cycle is not fully restored.

While the net 4 × 8 − 3 × 25 = 43 epact subtractions could be distributed evenly over 10,000 years (as has been proposed for example by Dr. Heiner Lichtenberg).^[40], if the corrections are combined, then the inaccuracies of the two cycles are also added and can not be corrected separately.

The ratios of (mean solar) days per year and days per lunation change both because of intrinsic long-term variations in the orbits, and because the rotation of the Earth is slowing down due to tidal deceleration, so the Gregorian parameters become increasingly obsolete.

This does affect the date of the equinox, but it so happens that the interval between northward (northern hemisphere spring) equinoxes has been fairly stable over historical times, especially if measured in mean solar time (see,^[41] esp.^[42])

Also the drift in ecclesiastical full moons calculated by the Gregorian method compared to the true full moons is affected less than one would expect, because the increase in the length of the day is almost exactly compensated for by the increase in the length of the month, as tidal braking transfers angular momentum of the rotation of the Earth to orbital angular momentum of the Moon.

The Ptolemaic value of the length of the mean synodic month, established around the 4th century BCE by the Babylonians, is 29 days 12 hr 44 min 3+1/3 s (see Kidinnu); the current value is 0.46 s less (see New moon). In the same historic stretch of time the length of the mean tropical year has diminished by about 10 s (all values mean solar time).

British Calendar Act and Book of Common Prayer

The portion of the Tabular methods section above describes the historical arguments and methods by which the present dates of Easter Sunday were decided in the late 16th century by the Catholic Church. In Britain, where the Julian calendar was then still in use, Easter Sunday was defined, from 1662 to 1752 (in accordance with previous practice), by a simple table of dates in the Anglican Prayer Book (decreed by the Act of Uniformity 1662). The table was indexed directly by the golden number and the Sunday letter, which (in the Easter section of the book) were presumed to be already known.

For the British Empire and colonies, the new determination of the Date of Easter Sunday was defined by what is now called the Calendar (New Style) Act 1750 with its Annexe. The method was chosen to give dates agreeing with the Gregorian rule already in use elsewhere. The Act required that it be put in the Book of Common Prayer, and therefore it is the general Anglican rule. The original Act can be seen in the British Statutes at Large 1765.^[43] The Annexe to the Act includes the definition: "Easter-day (on which the rest depend) is always the first Sunday after the Full Moon, which happens upon, or next after the Twenty-first Day of March. And if the Full Moon happens upon a Sunday, Easter-day is the Sunday after." The Annexe subsequently uses the terms "Paschal Full Moon" and "Ecclesiastical Full Moon", making it clear that they approximate to the real full moon.

The method is quite distinct from that described above in Gregorian calendar. For a general year, one first determines the golden number, then one uses three tables to determine the Sunday letter, a "cypher", and the date of the paschal full moon, from which the date of Easter Sunday follows. The epact does not explicitly appear. Simpler tables can be used for limited periods (such as 1900–2199) during which the cypher (which represents the effect of the solar and lunar corrections) does not change. Clavius' details were employed in the construction of the method, but they play no subsequent part in its use.^[44][45]

J. R. Stockton shows his derivation of an efficient computer algorithm traceable to the tables in the Prayer Book and the Calendar Act (assuming that a description of how to use the Tables is at hand), and verifies its processes by computing matching Tables.^[46]

4.2. Julian Calendar

 

Distribution of the date of Easter in most eastern churches 1900–2099 vs western Easter distribution. https://handwiki.org/wiki/index.php?curid=1196013

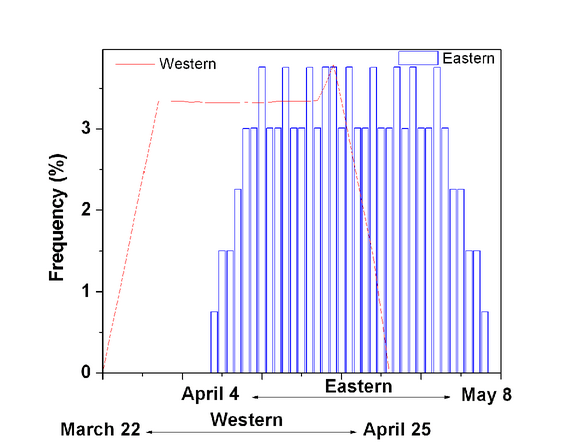
The method for computing the date of the ecclesiastical full moon that was standard for the western Church before the Gregorian calendar reform, and is still used today by most eastern Christians, made use of an uncorrected repetition of the 19-year Metonic cycle in combination with the Julian calendar. In terms of the method of the epacts discussed above, it effectively used a single epact table starting with an epact of 0, which was never corrected. In this case, the epact was counted on 22 March, the earliest acceptable date for Easter. This repeats every 19 years, so there are only 19 possible dates for the paschal full moon from 21 March to 18 April inclusive.

Because there are no corrections as there are for the Gregorian calendar, the ecclesiastical full moon drifts away from the true full moon by more than three days every millennium. It is already a few days later. As a result, the eastern churches celebrate Easter one week later than the western churches about 50% of the time. (The eastern Easter is occasionally four or five weeks later because the Julian calendar is 13 days behind the Gregorian in 1900–2099, and so the Gregorian paschal full moon is sometimes before Julian 21 March.)

The sequence number of a year in the 19-year cycle is called its golden number. This term was first used in the computistic poem Massa Compoti by Alexander de Villa Dei in 1200. A later scribe added the golden number to tables originally composed by Abbo of Fleury in 988.

The claim by the Catholic Church in the 1582 papal bull Inter gravissimas, which promulgated the Gregorian calendar, that it restored "the celebration of Easter according to the rules fixed by ... the great ecumenical council of Nicaea"^[47] was based on a false claim by Dionysius Exiguus (525) that "we determine the date of Easter Day ... in accordance with the proposal agreed upon by the 318 Fathers of the Church at the Council in Nicaea."^[48] The First Council of Nicaea (325) did not, however, provide any explicit rules to determine that date, but only wrote “all our brethren in the East who formerly followed the custom of the Jews are henceforth to celebrate the said most sacred feast of Easter at the same time with the Romans and yourselves [the Church of Alexandria] and all those who have observed Easter from the beginning.”^[49] The medieval computus was based on the Alexandrian computus, which was developed by the Church of Alexandria during the first decade of the 4th century using the Alexandrian calendar.^[50]:36 The eastern Roman Empire accepted it shortly after 380 after converting the computus to the Julian calendar.^[50]:48 Rome accepted it sometime between the sixth and ninth centuries. The British Isles accepted it during the eighth century except for a few monasteries. Francia (all of western Europe except Scandinavia (pagan), the British Isles, the Iberian peninsula, and southern Italy) accepted it during the last quarter of the eighth century. The last Celtic monastery to accept it, Iona, did so in 716, whereas the last English monastery to accept it did so in 931. Before these dates, other methods produced Easter Sunday dates that could differ by up to five weeks.

This is the table of paschal full moon dates for all Julian years since 931:

Golden number	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
Paschal full moon date	5 April	25 March	13 April	2 April	22 March	10 April	30 March	18 April	7 April	27 March	15 April	4 April	24 March	12 April	1 April	21 March	9 April	29 March	17 April

Example calculation using this table:

The golden number for 1573 is 16 (1573 + 1 = 1574; 1574 ÷ 19 = 82 remainder 16). From the table, the paschal full moon for golden number 16 is 21 March. From the week table 21 March is Saturday. Easter Sunday is the following Sunday, 22 March.

So for a given date of the ecclesiastical full moon, there are seven possible Easter dates. The cycle of Sunday letters, however, does not repeat in seven years: because of the interruptions of the leap day every four years, the full cycle in which weekdays recur in the calendar in the same way, is 4 × 7 = 28 years, the so-called solar cycle. So the Easter dates repeated in the same order after 4 × 7 × 19 = 532 years. This paschal cycle is also called the Victorian cycle, after Victorius of Aquitaine, who introduced it in Rome in 457. It is first known to have been used by Annianus of Alexandria at the beginning of the 5th century. It has also sometimes erroneously been called the Dionysian cycle, after Dionysius Exiguus, who prepared Easter tables that started in 532; but he apparently did not realize that the Alexandrian computus he described had a 532-year cycle, although he did realize that his 95-year table was not a true cycle. Venerable Bede (7th century) seems to have been the first to identify the solar cycle and explain the paschal cycle from the Metonic cycle and the solar cycle.

In medieval western Europe, the dates of the paschal full moon (14 Nisan) given above could be memorized with the help of a 19-line alliterative poem in Latin:^[51][52]

Nonae Aprilis	norunt quinos	V
octonae kalendae	assim depromunt.	I
Idus Aprilis	etiam sexis,	VI
nonae quaternae	namque dipondio.	II
Item undene	ambiunt quinos,	V
quatuor idus	capiunt ternos.	III
Ternas kalendas	titulant seni,	VI
quatuor dene	cubant in quadris.	IIII
Septenas idus	septem eligunt,	VII
senae kalendae	sortiunt ternos,	III
denis septenis	donant assim.	I
Pridie nonas	porro quaternis,	IIII
nonae kalendae	notantur septenis.	VII
Pridie idus	panditur quinis,	V
kalendas Aprilis	exprimunt unus.	I
Duodene namque	docte quaternis,	IIII
speciem quintam	speramus duobus.	II
Quaternae kalendae	quinque coniciunt,	V
quindene constant	tribus adeptis.	III

The first half-line of each line gives the date of the paschal full moon from the table above for each year in the 19-year cycle. The second half-line gives the ferial regular, or weekday displacement, of the day of that year's paschal full moon from the concurrent, or the weekday of 24 March.^[1]:xlvii The ferial regular is repeated in Roman numerals in the third column.

5. Algorithms

5.1. Note on Operations

When expressing Easter algorithms without using tables, it has been customary to employ only the integer operations addition, subtraction, multiplication, division, modulo, and assignment (plus, minus, times, div, mod, assign) as it is compatible with the use of simple mechanical or electronic calculators. That restriction is undesirable for computer programming, where conditional operators and statements, as well as look-up tables, are available. One can easily see how conversion from day-of-March (22 to 56) to day-and-month (22 March to 25 April) can be done as (if DoM>31) {Day=DoM-31, Month=Apr} else {Day=DoM, Month=Mar}. More importantly, using such conditionals also simplifies the core of the Gregorian calculation.

5.2. Gauss' Easter Algorithm

In 1800, the mathematician Carl Friedrich Gauss presented this algorithm for calculating the date of the Julian or Gregorian Easter.^[53][54] He corrected the expression for calculating the variable p in 1816.^[55] In 1800, he incorrectly stated p = floor (k/3) = ⌊k/3⌋. In 1807, he replaced the condition (11M + 11) mod 30 < 19 with the simpler a > 10. In 1811, he limited his algorithm to the 18th and 19th centuries only, and stated that 26 April is always replaced with 19 April and 25 April by 18 April. In 1816, he thanked his student Peter Paul Tittel for pointing out that p was wrong in the original version.^[56]

Expression	year = 1777
a = year mod 19	a = 10
b = year mod 4	b = 1
c = year mod 7	c = 6
k = ⌊year/100⌋	k = 17
p = ⌊13 + 8k/25⌋	p = 5
q = ⌊k/4⌋	q = 4
M = (15 − p + k − q) mod 30	M = 23
N = (4 + k − q) mod 7	N = 3
d = (19a + M) mod 30	d = 3
e = (2b + 4c + 6d + N) mod 7	e = 5
Gregorian Easter is 22 + d + e March or d + e − 9 April	30 March
if d = 29 and e = 6, replace 26 April with 19 April
if d = 28, e = 6, and (11M + 11) mod 30 < 19, replace 25 April with 18 April
For the Julian Easter in the Julian calendar M = 15 and N = 6 (k, p, and q are unnecessary)

An analysis of the Gauss's Easter algorithm is divided into two parts. The first part is the approximate tracking of the lunar orbiting and the second part is the exact deterministic offsetting to obtain a Sunday following the full moon.

The first part consists of determining the variable d, the number of days (counting from March 21) for the closest following full moon to occur. The formula for d contains the terms 19a and the constant M. a is the year's position in the 19-year lunar phase cycle, in which by assumption the moon's movement relative to earth repeats every 19 calendar years. In older times, 19 calendar years were equated to 235 lunar months (the Metonic cycle), which is remarkably close since 235 lunar months are approximately 6939.6813 days and 19 years are on average 6939.6075 days. The expression (19a + M) mod 30 repeats every 19 years within each century as M is determined per century. The 19-year cycle has nothing to do with the '19' in 19a, it is just a coincidence that another '19' appears. The '19' in 19a comes from correcting the mismatch between a calendar year and an integer number of lunar months. A calendar year (non-leap year) has 365 days and the closest you can come with an integer number of lunar months is 12 × 29.5 = 354 days. The difference is 11 days, which must be corrected for by moving the following year's occurrence of a full moon 11 days back. But in modulo 30 arithmetic, subtracting 11 is the same as adding 19, hence the addition of 19 for each year added, i.e. 19a.

The M in 19a + M serves to have a correct starting point at the start of each century. It is determined by a calculation taking the number of leap years up until that century where k inhibits a leap day every 100 years and q reinstalls it every 400 years, yielding (k − q) as the total number of inhibitions to the pattern of a leap day every four years. Thus we add (k − q) to correct for leap days that never occurred. p corrects for the lunar orbit not being fully describable in integer terms.

The range of days considered for the full moon to determine Easter are 21 March (the day of the ecclesislastical equinox of spring) to 19 April—a 30-day range mirrored in the mod 30 arithmetic of variable d and constant M, both of which can have integer values in the range 0 to 29. Once d is determined, this is the number of days to add to 21 March (the earliest possible full moon allowed, which is coincident with the ecclesiastical equinox of spring) to obtain the day of the full moon.

So the first allowable date of Easter is 21+d+1, as Easter is to celebrate the Sunday after the ecclesiastical full moon, that is if the full moon falls on Sunday 21 March Easter is to be celebrated 7 days after, while if the full moon falls on Saturday 21 March Easter is the following 22 March.

The second part is finding e, the additional offset days that must be added to the date offset d to make it arrive at a Sunday. Since the week has 7 days, the offset must be in the range 0 to 6 and determined by modulo 7 arithmetic. e is determined by calculating 2b + 4c + 6d + N mod 7. These constants may seem strange at first, but are quite easily explainable if we remember that we operate under mod 7 arithmetic. To begin with, 2b + 4c ensures that we take care of the fact that weekdays slide for each year. A normal year has 365 days, but 52 × 7 = 364, so 52 full weeks make up one day too little. Hence, each consecutive year, the weekday "slides one day forward", meaning if May 6 was a Wednesday one year, it is a Thursday the following year (disregarding leap years). Both b and c increases by one for an advancement of one year (disregarding modulo effects). The expression 2b + 4c thus increases by 6 – but remember that this is the same as subtracting 1 mod 7. To subtract by 1 is exactly what is required for a normal year – since the weekday slips one day forward we should compensate one day less to arrive at the correct weekday (i.e. Sunday). For a leap year, b becomes 0 and 2b thus is 0 instead of 8 – which under mod 7, is another subtraction by 1 – i.e., a total subtraction by 2, as the weekdays after the leap day that year slides forward by two days.

The expression 6d works the same way. Increasing d by some number y indicates that the full moon occurs y days later this year, and hence we should compensate y days less. Adding 6d is mod 7 the same as subtracting d, which is the desired operation. Thus, again, we do subtraction by adding under modulo arithmetic. In total, the variable e contains the step from the day of the full moon to the nearest following Sunday, between 0 and 6 days ahead. The constant N provides the starting point for the calculations for each century and depends on where Jan 1, year 1 was implicitly located when the Gregorian calendar was constructed.

The expression d + e can yield offsets in the range 0 to 35 pointing to possible Easter Sundays on March 22 to April 26. For reasons of historical compatibility, all offsets of 35 and some of 34 are subtracted by 7, jumping one Sunday back to the day before the full moon (in effect using a negative e of −1). This means that 26 April is never Easter Sunday and that 19 April is overrepresented. These latter corrections are for historical reasons only and has nothing to do with the mathematical algorithm.

Using the Gauss's Easter algorithm for years prior to 1583 is historically pointless since the Gregorian calendar was not utilised for determining Easter before that year. Using the algorithm far into the future is questionable, since we know nothing about how different churches will define Easter far ahead. Easter calculations are based on agreements and conventions, not on the actual celestial movements nor on indisputable facts of history.

5.3. Anonymous Gregorian Algorithm

"A New York correspondent" submitted this algorithm for determining the Gregorian Easter to the journal Nature in 1876.^[56][57] It has been reprinted many times, e.g., in 1877 by Samuel Butcher in The Ecclesiastical Calendar,^[58]:225 in 1916 by Arthur Downing in The Observatory,^[59] in 1922 by H. Spencer Jones in General Astronomy,^[60] in 1977 by the Journal of the British Astronomical Association,^[61] in 1977 by The Old Farmer's Almanac, in 1988 by Peter Duffett-Smith in Practical Astronomy with your Calculator, and in 1991 by Jean Meeus in Astronomical Algorithms.^[62] Because of the Meeus book citation, this is also called "Meeus/Jones/Butcher" algorithm:

Expression	Y = 1961	Y = 2022
a = Y mod 19	a = 4	a = 8
b = Y div 100	b = 19	b = 20
c = Y mod 100	c = 61	c = 22
d = b div 4	d = 4	d = 5
e = b mod 4	e = 3	e = 0
f = (b + 8) div 25	f = 1	f = 1
g = (b − f + 1) div 3	g = 6	g = 6
h = (19a + b − d − g + 15) mod 30	h = 10	h = 26
i = c div 4	i = 15	i = 5
k = c mod 4	k = 1	k = 2
ℓ = (32 + 2e + 2i − h − k) mod 7	ℓ = 1	ℓ = 0
m = (a + 11h + 22ℓ) div 451	m = 0	m = 0
month = (h + ℓ − 7m + 114) div 31	month = 4 (April)	month = 4 (April)
day = ((h + ℓ − 7m + 114) mod 31) + 1	day = 2	day = 17
Gregorian Easter	2 April 1961	17 April 2022

In 1961 the New Scientist published a version of the Nature algorithm incorporating a few changes.^[63] The variable g was calculated using Gauss' 1816 correction, resulting in the elimination of variable f. Some tidying results in the replacement of variable o (to which one must be added to obtain the date of Easter) with variable p, which gives the date directly.

5.4. Meeus's Julian Algorithm

Jean Meeus, in his book Astronomical Algorithms (1991, p. 69), presents the following algorithm for calculating the Julian Easter on the Julian Calendar, which is not the Gregorian Calendar used throughout the contemporary world. To obtain the date of Eastern Orthodox Easter on the latter calendar, 13 days (as of 1900 through 2099) must be added to the Julian dates, producing the dates below, in the last row.

Expression	Y = 2008	Y = 2009	Y = 2010	Y = 2011	Y = 2016
a = Y mod 4	a = 0	a = 1	a = 2	a = 3	a = 0
b = Y mod 7	b = 6	b = 0	b = 1	b = 2	b = 0
c = Y mod 19	c = 13	c = 14	c = 15	c = 16	c = 2
d = (19c + 15) mod 30	d = 22	d = 11	d = 0	d = 19	d = 23
e = (2a + 4b − d + 34) mod 7	e = 1	e = 4	e = 0	e = 1	e = 4
month = (d + e + 114) div 31	4 (April)	4 (April)	3 (March)	4 (April)	4 (April)
day = ((d + e + 114) mod 31) + 1	14	6	22	11	18
Easter Day (Julian calendar)	14 April 2008	6 April 2009	22 March 2010	11 April 2011	18 April 2016
Easter Day (Gregorian calendar)	27 April 2008	19 April 2009	4 April 2010	24 April 2011	1 May 2016