Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1 handwiki
Camila Xu
 -- 1676 2022-11-15 01:38:03

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
HandWiki. Phase Curve. Encyclopedia. Available online: https://encyclopedia.pub/entry/34629 (accessed on 15 November 2024).
HandWiki. Phase Curve. Encyclopedia. Available at: https://encyclopedia.pub/entry/34629. Accessed November 15, 2024.
HandWiki. "Phase Curve" Encyclopedia, https://encyclopedia.pub/entry/34629 (accessed November 15, 2024).
HandWiki. (2022, November 15). Phase Curve. In Encyclopedia. https://encyclopedia.pub/entry/34629
HandWiki. "Phase Curve." Encyclopedia. Web. 15 November, 2022.
Phase Curve
Edit
The content is sourced from: https://handwiki.org/wiki/Physics:Phase_curve

In astronomy a phase curve describes the brightness of a reflecting body as a function of its phase angle. The brightness usually refers the object's absolute magnitude, which, in turn, is its apparent magnitude at a distance of astronomical unit from the Earth and Sun. The phase angle equals the arc subtended by the observer and the sun as measured at the body. The phase curve is useful for characterizing an object's regolith (soil) and atmosphere. It is also the basis for computing the geometrical albedo and the Bond albedo of the body. In ephemeris generation, the phase curve is used in conjunction with the distances from the object to the Sun and the Earth to calculate the apparent magnitude.

phase angle regolith albedo

1. Mercury

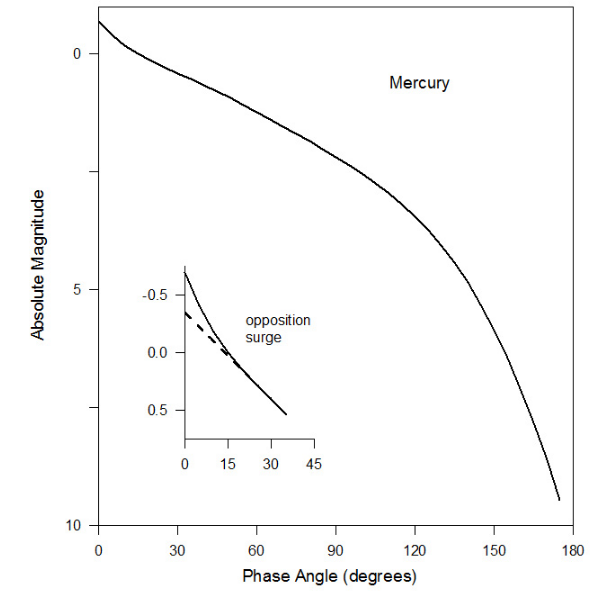
The phase curve of Mercury and its opposition surge.[1] https://handwiki.org/wiki/index.php?curid=1785483

The phase curve of Mercury is very steep, which is characteristic of a body on which bare regolith (soil) is exposed to view. At phase angles exceeding 90° (crescent phase) the brightness falls off especially sharply. The shape of the phase curve indicates a mean slope on the surface of Mercury of about 16°,[1] which is slightly smoother than that of the Moon. Approaching phase angle 0° (fully illuminated phase) the curve rises to a sharp peak. This surge in brightness is called the opposition effect[2][3] because for most bodies (though not Mercury) it occurs at astronomical opposition when the body is opposite from the Sun in the sky. The width of the opposition surge for Mercury indicates that both the compaction state of the regolith and the distribution of particle sizes on the planet are similar to those on the Moon.[1]

Early visual observations contributing to the phase curve of Mercury were obtained by G. Muller[4] in the 1800s and by André-Louis Danjon[5][6][7] in the mid-twentieth century. W. Irvine and colleagues[8] used photoelectric photometry in the 1960s. Some of these early data were analyzed by G. de Vaucouleurs,[9][10] summarized by D. Harris[11] and used for predicting apparent magnitudes in the Astronomical Almanac[12] for several decades. Highly accurate new observations covering the widest range of phase angles to date (2 to 170°) were carried out by A. Mallama, D. Wang and R. Howard[1] using the Large Angle and Spectrometric Coronograph (LASCO) on the Solar and Heliospheric Observatory (SOHO) satellite. They also obtained new CCD observations from the ground. These data are now the major source of the phase curve used in the Astronomical Almanac[13] for predicting apparent magnitudes.

The apparent brightness of Mercury as seen from Earth is greatest at phase angle 0° (superior conjunction with the Sun) when it can reach magnitude −2.6.[14] At phase angles approaching 180° (inferior conjunction) the planet fades to about magnitude +5[14] with the exact brightness depending on the phase angle at that particular conjunction. This difference of more than 7 magnitudes corresponds to a change of over a thousand times in apparent brightness.

2. Venus

The phase curve of Venus[15] compared to Mercury,[1] and the brightness excess of Venus. https://handwiki.org/wiki/index.php?curid=1384524

The relatively flat phase curve of Venus is characteristic of a cloudy planet.[14] In contrast to Mercury where the curve is strongly peaked approaching phase angle zero (full phase) that of Venus is rounded. The wide illumination scattering angle of clouds, as opposed to the narrower scattering of regolith, causes this flattening of the phase curve. Venus exhibits a brightness surge near phase angle 170°, when it is a thin crescent, due to forward scattering of sunlight by droplets of sulfuric acid that are above the planet's cloud tops.[15] Even beyond 170° the brightness does not decline very steeply.

The history of observation and analysis of the phase curve of Venus is similar to that of Mercury. The best set of modern observations and interpretation was reported by A. Mallama, D. Wang and R. Howard.[15] They used the LASCO instrument on SOHO and ground-based, CCD equipment to observe the phase curve from 2 to 179°. As with Mercury, these new data are the major source of the phase curve used in the Astronomical Almanac[13] for predicting apparent magnitudes.

In contrast to Mercury the maximal apparent brightness of Venus as seen from Earth does not occur at phase angle zero. Since the phase curve of Venus is relatively flat while its distance from the Earth can vary greatly, maximum brightness occurs when the planet is a crescent, at phase angle 125°, at which time Venus can be as bright as magnitude −4.9.[14] Near inferior conjunction the planet typically fades to about magnitude −3[14] although the exact value depends on the phase angle. The typical range in apparent brightness for Venus over the course of one apparition is less than a factor of 10 or merely 1% that of Mercury.

3. Earth

The phase curve of the Earth has not been determined as accurately as those for Mercury and Venus because its integrated brightness is difficult to measure from the surface. Instead of direct observation, earthshine reflected from the portion of the Moon not lit by the Sun has served as a proxy. A few direct measurements of the Earth's luminosity have been obtained with the EPOXI spacecraft. While they do not cover much of the phase curve they reveal a rotational light curve caused by the transit of dark oceans and bright land masses across the hemisphere. P. Goode and colleagues at Big Bear Solar Observatory have measured the earthshine[16] and T. Livengood of NASA analyzed the EPOXI data.[17]

Earth as seen from Venus near opposition from the Sun would be extremely bright at magnitude −6. To an observer outside the Earth's orbit on Mars our planet would appear most luminous near the time of its greatest elongation from the Sun, at about magnitude −1.5.

4. Mars

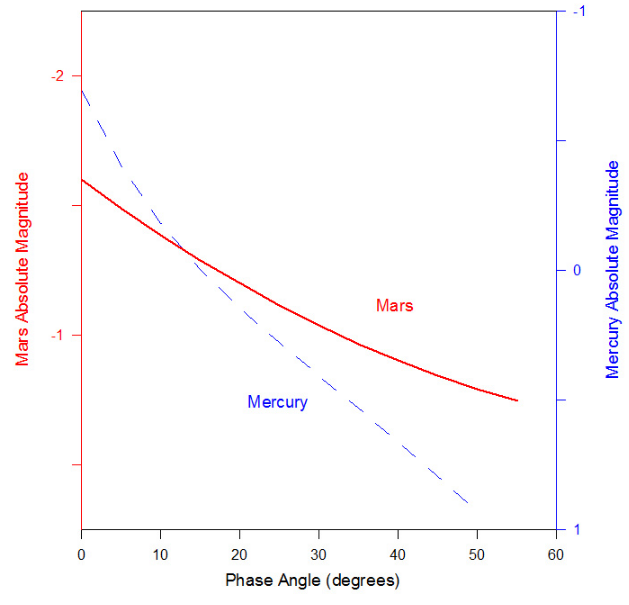
The phase curve of Mars[18] compared to Mercury.[1] https://handwiki.org/wiki/index.php?curid=1437927

Only about 50° of the martian phase curve can be observed from Earth because it orbits farther from the Sun than our planet. There is an opposition surge but it is less pronounced than that of Mercury. The rotation of bright and dark surface markings across its disk and variability of its atmospheric state (including its dust storms) superimpose variations on the phase curve. R. Schmude[19][20] obtained many of the Mars brightness measurements used in a comprehensive phase curve analysis performed by A. Mallama.[18]

Because the orbit of Mars is considerably eccentric its brightness at opposition can range from magnitude −3.0 to −1.4.[14] The minimum brightness is about magnitude +1.6[14] when Mars is on the opposite site of the Sun from the Earth. Rotational variations can elevate or suppress the brightness of Mars by 5% and global dust storms can increase its luminosity by 25%.[14][18]

5. Gas Giants

The outermost planets (Jupiter, Saturn, Uranus, and Neptune) are so distant that only small portions of their phase curves near 0° (full phase) can be evaluated from the Earth. That part of the curve is generally fairly flat, like that of Venus, for these cloudy planets.

The apparent magnitude of Jupiter ranges from −2.9 to −1.4, Saturn from −0.5 to +1.4, Uranus from +5.3 to +6.0, and Neptune from +7.8 to +8.0. Most of these variations are due to distance. However, the magnitude range for Saturn also depends on its ring system as explained below.

 

6. The Rings of Saturn

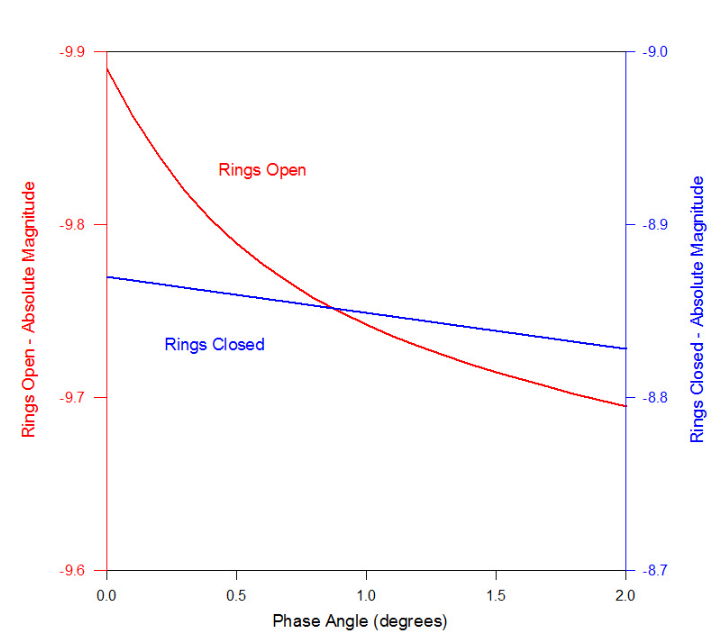
The phase curve of Saturn, according to Schmude[21] demonstrating the opposition effect of the ring system. https://handwiki.org/wiki/index.php?curid=1226368

The brightness of the Saturn system depends on the orientation of its ring system. The rings contribute more to the overall brightness of the system when they are more inclined to the direction of illumination from the Sun and to the view of the observer. Wide open rings contribute about one magnitude of brightness to the disk alone.[14] The icy particles that compose the rings also produce a strong opposition surge. Hubble Space Telescope and Cassini spacecraft images have been analyzed in an attempt to characterize the ring particles based on their phase curves.[22][23][24][25]

7. The Moon

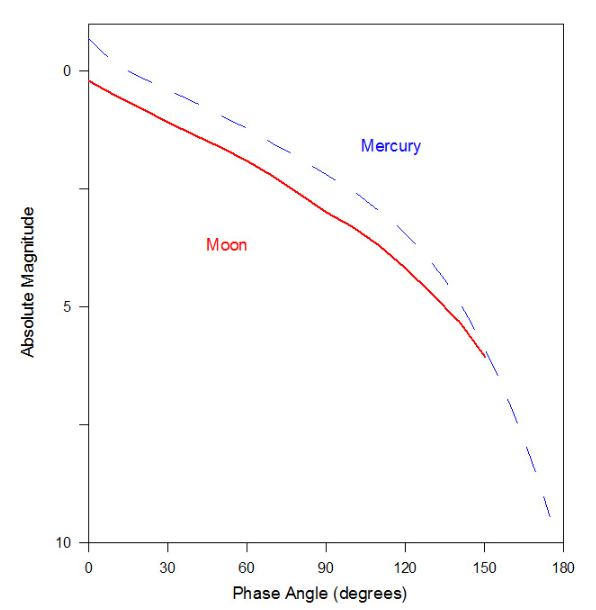
The phase curve of the Moon[26] compared to Mercury.[1] https://handwiki.org/wiki/index.php?curid=1313186

The phase curve of the Moon approximately resembles that of Mercury due to the similarities of the surfaces and the lack of an atmosphere on either body.[27] Clementine spacecraft data analyzed by J. Hillier, B. Buratti and K. Hill[28] indicate a lunar opposition surge. The Moon's apparent magnitude at full phase is −12.7[29] while at quarter phase it is 21 percent as bright.[26]

8. Planetary Satellites

The phase curves of many natural satellites of other planets[30][31] have been observed and interpreted. The icy moons often exhibit opposition brightness surges. This behavior has been used to model their surfaces.

9. Asteroids

The phase curves of many asteroids[32] have also been observed and they too may exhibit opposition surges. Asteroids can be physically classified in this way.[33] The effects of rotation can be very large and have to be factored in before the phase curve is computed. An example of such a study is reported by R. Baker and colleagues.[34]

10. Exoplanets

Programs for characterizing planets outside of the solar system depend largely on spectroscopy to identify atmospheric constituents and states, especially those that point to the presence of life forms or which could support life. However, brightness can be measured for very distant Earth-sized objects that are too faint for spectroscopic analysis. A. Mallama[35] has demonstrated that phase curve analysis may be a useful tool for identifying planets that are Earth-like. Additionally, J. Bailey[36] has pointed out that phase curve anomalies such as the brightness excess of Venus could be useful indicators of atmospheric constituents such as water, which might be essential to life in the universe.

11. Criticisms on Phase Curve Modelling

Inferences about regoliths from phase curves are frequently based on Hapke parameterization. However, in a blind test M. Shepard and P. Helfenstein[37] found no strong evidence that a particular set of Hapke parameters derived from photometric data could uniquely reveal the physical state of laboratory samples. These tests included modeling the three-term Henyey-Greenstein phase functions and the coherent backscatter opposition effect. This negative finding suggests that the radiative transfer model developed by B. Hapke may be inadequate for physical modeling based on photometry.

References

  1. Mallama, A.; Wang, D.; Howard, R.A. (2002). "Photometry of Mercury from SOHO/LASCO and Earth". Icarus 155 (2): 253–264. doi:10.1006/icar.2001.6723. Bibcode: 2002Icar..155..253M.  https://dx.doi.org/10.1006%2Ficar.2001.6723
  2. Shkuratov, Y. G., M. A. Kreslavsky, A. A. Ovcharenko, D. G. Stankevich, and E. S. Zubko (1999). "Opposition Effect from Clementine Data and Mechanisms of Backscatter". Icarus 141 (1): 132–155. doi:10.1006/icar.1999.6154. Bibcode: 1999Icar..141..132S.  https://dx.doi.org/10.1006%2Ficar.1999.6154
  3. Helfenstein, P., Veverka, J., and Hillier, J. (1997). "The lunar opposition effect: A test of alternative models". Icarus 128 (1): 2–14. doi:10.1006/icar.1997.5726. Bibcode: 1997Icar..128....2H.  https://dx.doi.org/10.1006%2Ficar.1997.5726
  4. Muller, G. (1893). "Helligkeitsbestimmungen der grossen planeten und einiger asteroiden". Publ. Astrophys. Obs. Potsdam 8 (92): 197–398. 
  5. Danjon, A. (1949). "Photometrie et colorimetrie des planetes Mercure et Venus". Bull. Astron. 14: 315–345. Bibcode: 1949BuAst..14..315D.  http://adsabs.harvard.edu/abs/1949BuAst..14..315D
  6. Danjon, A. (1950). "Correction to Danjon 1949". Bull. Astron. 14: 315. 
  7. Danjon, A. (1953). "Correction to Danjon 1949". Bull. Astron. 17: 363. 
  8. Irvine, W. H., T. Simon, D. H. Menzel, C. Pikoos, and A. T. Young (1968). "Multicolor photoelectric photometry of the brighter planets III". Astron. J. 73: 807–828. doi:10.1086/110702. Bibcode: 1968AJ.....73..807I.  https://dx.doi.org/10.1086%2F110702
  9. de Vaucouleurs, G. (1964). "Geometric and photometric parameters of the terrestrial planets". Icarus 3 (3): 187–235. doi:10.1016/0019-1035(64)90018-1. Bibcode: 1964Icar....3..187D.  https://dx.doi.org/10.1016%2F0019-1035%2864%2990018-1
  10. deVaucouleurs, G. (1970). A. Dollfus. ed. in Surface and Interiors of the Planets and Satellites. Academic Press. p. 225. 
  11. Harris, D.L. (1961). G.P. Kuiper & B.A. Middlehurst. ed. in Planets and Satellites. U. Chicago Press. p. 272. 
  12. Hilton, J.L. (1992). P.K. Seidelmann. ed. in Explanatory Supplement to the Astronomical Almanac. University Science Books. p. 383. 
  13. Hilton, J.L. (2005). "Improving the visual magnitudes of the planets in the Astronomical Almanac. I. Mercury and Venus". Astron. J. 129 (6): 2902–2906. doi:10.1086/430212. Bibcode: 2005AJ....129.2902H.  https://dx.doi.org/10.1086%2F430212
  14. Mallama, A. (2011). "Planetary magnitudes". Sky and Telescope 121 (1): 51–56. 
  15. Mallama, A.; Wang, D.; Howard, R.A. (2006). "Venus phase function and forward scattering from H2SO4". Icarus 182 (1): 10–22. doi:10.1016/j.icarus.2005.12.014. Bibcode: 2006Icar..182...10M.  https://dx.doi.org/10.1016%2Fj.icarus.2005.12.014
  16. Goode, P.R., Qiu, J., Yurchyshyn, V., Hickey, J., Chu, M.C., Kolbe, E., Brown, C.T., and Koonin, S.E. (2001). "Earthshine observations of the Earth's reflectance". Geophys. Res. Lett. 28 (9): 1671–1674. doi:10.1029/2000GL012580. Bibcode: 2001GeoRL..28.1671G. https://authors.library.caltech.edu/50838/1/grl14388.pdf. 
  17. Livengood, T., and 10 co-authors (2008). "EPOXI empirical test of optical characterization of an Earth-like planet". Bull. Am. Astron. Soc. 40: Presentation 01.03. Bibcode: 2008DPS....40.0103L.  http://adsabs.harvard.edu/abs/2008DPS....40.0103L
  18. Mallama, A. (2007). "The magnitude and albedo of Mars". Icarus 192 (2): 404–416. doi:10.1016/j.icarus.2007.07.011. Bibcode: 2007Icar..192..404M.  https://dx.doi.org/10.1016%2Fj.icarus.2007.07.011
  19. Schmude , R.W. Jr. (2004). "ALPO observations of the 2003 apparition of Mars". J. Assoc. Lunar Planet. Observ. 46 (4): 28–42 and references therein. Bibcode: 2004JALPO..46d..28S.  http://adsabs.harvard.edu/abs/2004JALPO..46d..28S
  20. Schmude, R.W. Jr. (2006). "Wideband photometry of Mars: 1991–2006". Bull. Am. Astron. Soc. 38 (3): 600 and references therein. Bibcode: 2006DPS....38.6014S.  http://adsabs.harvard.edu/abs/2006DPS....38.6014S
  21. Schmude, R.W. Jr. (2011). "The magnitude and color of the Saturn system". Icarus 211 (1): 732–739. doi:10.1016/j.icarus.2010.09.018. Bibcode: 2011Icar..211..732S.  https://dx.doi.org/10.1016%2Fj.icarus.2010.09.018
  22. French, R.G., Verbiscer, A., Salo, H., McGhee, C., and Dones, L. (2007). "Saturn's rings at true opposition". Publ. Astron. Soc. Pac. 119 (856): 623–643. doi:10.1086/519982. Bibcode: 2007PASP..119..623F.  https://dx.doi.org/10.1086%2F519982
  23. Poulet, F., Cuzzi, J. N., French, R.G., Dones, L. (2002). "A study of Saturn's ring phase curves from HST observations". Icarus 158 (1): 224–248. doi:10.1006/icar.2002.6852. Bibcode: 2002Icar..158..224P. https://zenodo.org/record/1229850. 
  24. Cuzzi, J.N., French, R.G., Dones, L. (2002). "HST multicolor (255–1042 nm) photometry of Saturn's main rings". Icarus 158 (1): 199–223. doi:10.1006/icar.2002.6851. Bibcode: 2002Icar..158..199C. https://zenodo.org/record/1229848. 
  25. Salo, H.; French, R. G. (2010). "The opposition and tilt effects of Saturn's rings from HST observations". Icarus 210 (2): 785–816. doi:10.1016/j.icarus.2010.07.002. Bibcode: 2010Icar..210..785S.  https://dx.doi.org/10.1016%2Fj.icarus.2010.07.002
  26. Cox, A.N. (2000). Allen's Astrophysical Quantities, fourth edition. Springer-Verlag. pp. 307–310. 
  27. Warell, J. (2004). "Properties of the Hermean regolith: IV. Photometric parameters of Mercury and the Moon contrasted with Hapke modelling". Icarus 167 (2): 271–286. doi:10.1016/j.icarus.2003.10.010. Bibcode: 2004Icar..167..271W.  https://dx.doi.org/10.1016%2Fj.icarus.2003.10.010
  28. Hillier, J., Buratti B., and Hill, K. (1999). "Multispectral photometry of the Moon and absolute calibration of the Clementine UV/VIS camera". Icarus 141 (2): 205–225. doi:10.1006/icar.1999.6184. Bibcode: 1999Icar..141..205H.  https://dx.doi.org/10.1006%2Ficar.1999.6184
  29. Williams, Dr. David R. (2010-02-02). "Moon Fact Sheet". NASA (National Space Science Data Center). http://nssdc.gsfc.nasa.gov/planetary/factsheet/moonfact.html. 
  30. Bauer, J.M., Grav, T., Buratti, B.J. and Hicks, M.D. (2006). "The phase curve survey of the irregular saturnian satellites: A possible method of physical classification". Icarus 184 (1): 181–197. doi:10.1016/j.icarus.2006.04.011. Bibcode: 2006Icar..184..181B.  https://dx.doi.org/10.1016%2Fj.icarus.2006.04.011
  31. Deau, E., Dones, L., Rodriguez, S., Charnoz, S. and Brahic, A. (2009). "The opposition effect in the outer Solar system: A comparative study of the phase function morphology". Planetary and Space Science 57 (11): 1282–1301. doi:10.1016/j.pss.2009.05.005. Bibcode: 2009P&SS...57.1282D.  https://dx.doi.org/10.1016%2Fj.pss.2009.05.005
  32. Cox, A.N. (2000). Allen's Astrophysical Quantities, fourth edition. Springer-Verlag. p. 299. 
  33. Kaasalainen, S., Piironen, J., Kaasalainen, M., Harris, A.W., Muinonen, K. and Cellino, A. (2003). "Asteroid photometric and polarimetric phase curves: empirical interpretation". Icarus 161 (1): 34–46. doi:10.1016/S0019-1035(02)00020-9. Bibcode: 2003Icar..161...34K.  https://dx.doi.org/10.1016%2FS0019-1035%2802%2900020-9
  34. Baker, R.E., Benishek, V., Pilcher, F., and Higgins, D.; Benishek; Pilcher; Higgins (2010). "Rotation period and H-G parameters determination for 1700 Zvezdara: A collaborative photometry project". The Minor Planet Bulletin 37 (3): 81–83. Bibcode: 2010MPBu...37...81B. http://articles.adsabs.harvard.edu/pdf/2010MPBu...37...81B. 
  35. Mallama, A. (2009). "Characterization of terrestrial exoplanets based on the phase curves and albedos of Mercury, Venus and Mars". Icarus 204 (1): 11–14. doi:10.1016/j.icarus.2009.07.010. Bibcode: 2009Icar..204...11M.  https://dx.doi.org/10.1016%2Fj.icarus.2009.07.010
  36. Bailey, J. (2007). "Rainbows, polarization, and the search for habitable planets". Astrobiology 7 (2): 320–332. doi:10.1089/ast.2006.0039. PMID 17480163. Bibcode: 2007AsBio...7..320B.  https://dx.doi.org/10.1089%2Fast.2006.0039
  37. Shepard, M. K.; Helfenstein, P. (2007). "A test of the Hapke photometric model". J. Geophys. Res. 112 (E3): E03001. doi:10.1029/2005JE002625. Bibcode: 2007JGRE..112.3001S.  https://dx.doi.org/10.1029%2F2005JE002625
More
©Text is available under the terms and conditions of the Creative Commons-Attribution ShareAlike (CC BY-SA) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Nuclear Science & Technology
Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
HandWiki
View Times: 782
Entry Collection: HandWiki
Revision: 1 time (View History)
Update Date: 15 Nov 2022
Table of Contents
    1000/1000
    Hot Most Recent
    ScholarVision Creations
    Feedback