
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Camila Xu | -- | 1019 | 2022-11-11 01:46:05 |
Video Upload Options
To determine the vibrational spectroscopy of linear molecules, the rotation and vibration of linear molecules are taken into account to predict which vibrational (normal) modes are active in the infrared spectrum and the Raman spectrum.
1. Degrees of Freedom
The location of a molecule in a 3-dimensional space can be described by the total number of coordinates. Each atom is assigned a set of x, y, and z coordinates and can move in all three directions. Degrees of freedom is the total number of variables used to define the motion of a molecule completely. For N atoms in a molecule moving in 3-D space, there are 3N total motions because each atom has 3N degrees of freedom.[1]
2. Vibrational Modes
N atoms in a molecule have 3N degrees of freedom which constitute translations, rotations, and vibrations. For non-linear molecules, there are 3 degrees of freedom for translational (motion along the x, y, and z directions) and 3 degrees of freedom for rotational motion (rotations in Rx, Ry, and Rz directions) for each atom. Linear molecules are defined as possessing bond angles of 180°, so there are 3 degrees of freedom for translational motion but only 2 degrees of freedom for rotational motion because the rotation about its molecular axis leaves the molecule unchanged.[2] When subtracting the translational and rotational degrees of freedom, the degrees of vibrational modes is determined.
Number of degrees of vibrational freedom for nonlinear molecules: 3N-6
Number of degrees of vibrational freedom for linear molecules: 3N-5[3]
2.1. Symmetry of Vibrational Modes
All 3N degrees of freedom have symmetry relationships consistent with the irreducible representations of the molecule's point group.[1] A linear molecule is characterized as possessing a bond angle of 180° with either a C∞v or D∞h symmetry point group. Each point group has a character table that represents all of the possible symmetry of that molecule. Specifically for linear molecules, the two character tables are shown below:
| C∞v | E | 2C∞ | ... | ∞σv | linear, rotations | quadratics |
|---|---|---|---|---|---|---|
| A1=Σ+ | 1 | 1 | ... | 1 | z | x2+y2, z2 |
| A2=Σ− | 1 | 1 | ... | -1 | Rz | |
| E1=Π | 2 | 2cos(φ) | ... | 0 | (x, y) (Rx, Ry) | (xz, yz) |
| E2=Δ | 2 | 2cos(2φ) | ... | 0 | (x2-y2, xy) | |
| E3=Φ | 2 | 2cos(3φ) | ... | 0 | ||
| ... | ... | ... | ... | ... |
| D∞h | E | 2C∞ | ... | ∞σv | i | 2S∞ | ... | ∞C'2 | linear functions, rotations | quadratics |
|---|---|---|---|---|---|---|---|---|---|---|
| A1g=Σ+g | 1 | 1 | ... | 1 | 1 | 1 | ... | 1 | x2+y2, z2 | |
| A2g=Σ−g | 1 | 1 | ... | -1 | 1 | 1 | ... | -1 | Rz | |
| E1g=Πg | 2 | 2cos(φ) | ... | 0 | 2 | -2cos(φ) | ... | 0 | (Rx, Ry) | (xz, yz) |
| E2g=Δg | 2 | 2cos(2φ) | ... | 0 | 2 | 2cos(2φ) | ... | 0 | (x2-y2, xy) | |
| E3g=Φg | 2 | 2cos(3φ) | ... | 0 | 2 | -2cos(3φ) | ... | 0 | ||
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ||
| A1u=Σ+u | 1 | 1 | ... | 1 | -1 | -1 | ... | -1 | z | |
| A2u=Σ−u | 1 | 1 | ... | -1 | -1 | -1 | ... | 1 | ||
| E1u=Πu | 2 | 2cos(φ) | ... | 0 | -2 | 2cos(φ) | ... | 0 | (x, y) | |
| E2u=Δu | 2 | 2cos(2φ) | ... | 0 | -2 | -2cos(2φ) | ... | 0 | ||
| E3u=Φu | 2 | 2cos(3φ) | ... | 0 | -2 | 2cos(2φ) | ... | 0 | ||
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
However, these two character tables have infinite number of irreducible representations, so it is necessary to lower the symmetry to a subgroup that has related representations whose characters are the same for the shared operations in the two groups. A property that transforms as one representation in a group will transform as its correlated representation in a subgroup. Therefore, C∞v will be correlated to C2v and D∞h to D2h. The correlation table for each is shown below:
| C∞v | C2v |
|---|---|
| A1=Σ+ | A1 |
| A2=Σ− | A2 |
| E1=Π | B1+B2 |
| E2=Δ | A1+A2 |
| D∞h | D2h |
|---|---|
| Σ+g | Ag |
| Σ−g | B1g |
| Πg | B2g+B3g |
| Δg | Ag+B1g |
| Σ+u | B1u |
| Σ−u | Au |
| Πu | B2u+B3u |
| Δu | Au+B1u |
Once the point group of the linear molecule is determined and the correlated symmetry is identified, all symmetry element operations associated to that correlated symmetry's point group are performed for each atom to deduce the reducible representation of the 3N Cartsian displacement vectors. From the right side of the character table, the non-vibrational degrees of freedom, rotational (Rx and Ry) and translational (x, y, and z), are subtracted: Γvib = Γ3N - Γrot - Γtrans. This yields the Γvib, which is used to find the correct normal modes from the original symmetry, which is either C∞v or D∞h, using the correlation table above. Then, each vibrational mode can be identified as either IR or Raman active.
2.2. Vibrational Spectroscopy
A vibration will be active in the IR if there is a change in the dipole moment of the molecule and if it has the same symmetry as one of the x, y, z coordinates. To determine which modes are IR active, the irreducible representation corresponding to x, y, and z are checked with the reducible representation of Γvib.[4] IR mode is active if the same irreducible representation is present in both.
Furthermore, a vibration will be active in the Raman if there is a change in the polarizability of the molecule and if it has the same symmetry as one of the direct products of the x, y, z coordinates. To determine which modes are Raman active, the irreducible representation corresponding to xy, xz, yz, x2, y2, and z2 are checked with the reducible representation of Γvib.[4] Raman mode is active if the same irreducible representation is present in both.
3. Example
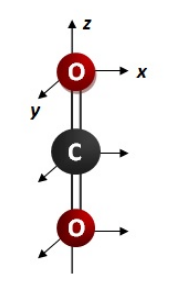
Carbon Dioxide, CO2
1. Assign point group: D∞h
2. Determine group-subgroup point group: D2h
3. Find the number of normal (vibrational) modes or degrees of freedom using the equation: 3n - 5 = 3(3) - 5 = 4
4. Derive reducible representation Γ3N:
| D2h | E | C2(z) | C2(y) | C2(x) | i | σ(xy) | σ(xz) | σ(yz) |
|---|---|---|---|---|---|---|---|---|
| Γ3N | 9 | -3 | -1 | -1 | -3 | 1 | 3 | 3 |
5. Decompose the reducible representation into irreducible components:
Γ3N = Ag + B2g + B3g + 2B1u + 2B2u + 2B3u
6. Solve for the irreducible representation corresponding to the normal modes with the subgroup character table:
Γ3N = Ag + B2g + B3g + 2B1u + 2B2u + 2B3u
Γrot = B2g + B3g
Γtrans = B1u + B2u + B3u
Γvib = Γ3N - Γrot - Γtrans
Γvib = Ag + B1u + B2u + B3u
7. Use the correlation table to find the normal modes for the original point group:
v1 = Ag = Σ+g
v2 = B1u = Σ+u
v3 = B2u = Πu
v4 = B3u = Πu
8. Label whether the modes are either IR active or Raman active:
v1 = Raman active
v2 = IR active
v3 = IR active
v4 = IR active
References
- Miessler, Gary L., Paul J. Fischer, and Donald A. Tarr. Inorganic Chemistry. Upper Saddle River: Pearson, 2014, 101.
- Holleman, A. F., and Egon Wiberg. Inorganic Chemistry. San Diego: Academic, 2001, 40.
- Housecroft, Catherine E., and A. G. Sharpe. Inorganic Chemistry. Upper Saddle River, NJ: Pearson Prentice Hall, 2005, 90.
- Kunju, A. Salahuddin. Group Theory and Its Applications in Chemistry. Delhi: Phi Learning, 2015, 83-86.




