1. Elaboration

In its most basic form, a moment is the product of the distance to a point, raised to a power, and a physical quantity (such as force or electrical charge) at that point:

[math]\displaystyle{ \mu_n = r^n\,Q, }[/math]

where [math]\displaystyle{ Q }[/math] is the physical quantity such as a force applied at a point, or a point charge, or a point mass, etc. If the quantity is not concentrated solely at a single point, the moment is the integral of that quantity's density over space:

[math]\displaystyle{ \mu_n = \int r^n \rho(r)\,dr }[/math]

where [math]\displaystyle{ \rho }[/math] is the distribution of the density of charge, mass, or whatever quantity is being considered.

More complex forms take into account the angular relationships between the distance and the physical quantity, but the above equations capture the essential feature of a moment, namely the existence of an underlying [math]\displaystyle{ r^n \rho(r) }[/math] or equivalent term. This implies that there are multiple moments (one for each value of n) and that the moment generally depends on the reference point from which the distance [math]\displaystyle{ r }[/math] is measured, although for certain moments (technically, the lowest non-zero moment) this dependence vanishes and the moment becomes independent of the reference point.

Each value of n corresponds to a different moment: the 1st moment corresponds to n = 1; the 2nd moment to n = 2, etc. The 0th moment (n = 0) is sometimes called the monopole moment; the 1st moment (n = 1) is sometimes called the dipole moment, and the 2nd moment (n = 2) is sometimes called the quadrupole moment, especially in the context of electric charge distributions.

1.1. Examples

• The moment of force, or torque, is a first moment: [math]\displaystyle{ \mathbf{\tau} = rF }[/math], or, more generally, [math]\displaystyle{ \mathbf{r} \times \mathbf{F} }[/math].
• Similarly, angular momentum is the 1st moment of momentum: [math]\displaystyle{ \mathbf{L} = \mathbf{r} \times \mathbf{p} }[/math]. Note that momentum itself is not a moment.
• The electric dipole moment is also a 1st moment: [math]\displaystyle{ \mathbf{p} = q\,\mathbf{d} }[/math] for two opposite point charges or [math]\displaystyle{ \int \mathbf{r}\,\rho(\mathbf{r})\,d^3r }[/math] for a distributed charge with charge density [math]\displaystyle{ \rho(\mathbf{r}) }[/math].

Moments of mass:

• The total mass is the zeroth moment of mass.
• The center of mass is the 1st moment of mass normalized by total mass: [math]\displaystyle{ \mathbf{R} = \frac 1M \sum_i \mathbf{r}_i m_i }[/math] for a collection of point masses, or [math]\displaystyle{ \frac 1M \int \mathbf{r} \rho(\mathbf{r}) \, d^3r }[/math] for an object with mass distribution [math]\displaystyle{ \rho(\mathbf{r}) }[/math].
• The moment of inertia is the 2nd moment of mass: [math]\displaystyle{ I = r^2 m }[/math] for a point mass, [math]\displaystyle{ \sum_i r_i^2 m_i }[/math] for a collection of point masses, or [math]\displaystyle{ \int r^2\rho(\mathbf{r}) \, d^3r }[/math] for an object with mass distribution [math]\displaystyle{ \rho(\mathbf{r}) }[/math]. Note that the center of mass is often (but not always) taken as the reference point.

2. Multipole Moments

Assuming a density function that is finite and localized to a particular region, outside that region a 1/r potential may be expressed as a series of spherical harmonics:

[math]\displaystyle{ \Phi(\mathbf{r}) = \int \frac{\rho(\mathbf{r'})}{|\mathbf{r}-\mathbf{r'}|} \, d^3r' = \sum_{\ell=0}^\infty \sum_{m=-\ell}^\ell \left( \frac{4\pi}{2\ell+1} \right) q_{\ell m}\, \frac{Y_{\ell m}(\theta, \varphi)}{r^{\ell+1}} }[/math]

The coefficients [math]\displaystyle{ q_{\ell m} }[/math] are known as multipole moments, and take the form:

[math]\displaystyle{ q_{\ell m} = \int (r')^\ell\, \rho(\mathbf{r'})\, Y^*_{\ell m}(\theta',\varphi')\, d^3r' }[/math]

where [math]\displaystyle{ \mathbf{r}' }[/math] expressed in spherical coordinates [math]\displaystyle{ \left(r', \varphi', \theta'\right) }[/math] is a variable of integration. A more complete treatment may be found in pages describing multipole expansion or spherical multipole moments. (Note: the convention in the above equations was taken from Jackson^[1] – the conventions used in the referenced pages may be slightly different.)

When [math]\displaystyle{ \rho }[/math] represents an electric charge density, the [math]\displaystyle{ q_{lm} }[/math] are, in a sense, projections of the moments of electric charge: [math]\displaystyle{ q_{00} }[/math] is the monopole moment; the [math]\displaystyle{ q_{1m} }[/math] are projections of the dipole moment, the [math]\displaystyle{ q_{2m} }[/math] are projections of the quadrupole moment, etc.

3. Applications of Multipole Moments

The multipole expansion applies to 1/r scalar potentials, examples of which include the electric potential and the gravitational potential. For these potentials, the expression can be used to approximate the strength of a field produced by a localized distribution of charges (or mass) by calculating the first few moments. For sufficiently large r, a reasonable approximation can be obtained from just the monopole and dipole moments. Higher fidelity can be achieved by calculating higher order moments. Extensions of the technique can be used to calculate interaction energies and intermolecular forces.

The technique can also be used to determine the properties of an unknown distribution [math]\displaystyle{ \rho }[/math]. Measurements pertaining to multipole moments may be taken and used to infer properties of the underlying distribution. This technique applies to small objects such as molecules,^[2][3] but has also been applied to the universe itself,^[4] being for example the technique employed by the WMAP and Planck experiments to analyze the cosmic microwave background radiation.

4. History

 

A lever in balance. https://handwiki.org/wiki/index.php?curid=1664350

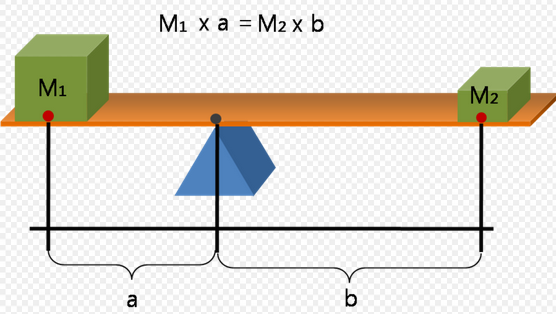
In works believed to stem from Ancient Greece , the concept of a moment is alluded to by the word ῥοπή (rhopḗ, lit. "inclination") and composites like ἰσόρροπα (isorropa, lit. "of equal inclinations").^[5][6][7] The context of these works is mechanics and geometry involving the lever.^[8] In particular, in extant works attributed to Archimedes, the moment is pointed out in phrasings like:

"Commensurable magnitudes (σύμμετρα μεγέθεα) [A and B] are equally balanced (ἰσορροπέοντι)^[9] if their distances [to the center Γ, i.e., ΑΓ and ΓΒ] are inversely proportional (ἀντιπεπονθότως) to their weights (βάρεσιν)."^[6][10]

Moreover, in extant texts such as The Method of Mechanical Theorems, moments are used to infer the center of gravity, area, and volume of geometric figures.

In 1269, William of Moerbeke translates various works of Archimedes and Eutocious into Latin. The term ῥοπή is transliterated into ropen.^[6]

Around 1450, Jacobus Cremonensis translates ῥοπή in similar texts into the Latin term momentum (lit. "movement"^[11]). The same term is kept in a 1501 translation by Giorgio Valla, and subsequently by Francesco Maurolico, Federico Commandino, Guidobaldo del Monte, Adriaan van Roomen, Florence Rivault, Francesco Buonamici, Marin Mersenne^[5], and Galileo Galilei. That said, why was the word momentum chosen for the translation? One clue, according to Treccani, is that momento in Medieval Italy, the place the early translators lived, in a transferred sense meant both a "moment of time" and a "moment of weight" (a small amount of weight that turns the scale).^[12]

In 1554, Francesco Maurolico clarifies the Latin term momentum in the work Prologi sive sermones. Here is a Latin to English translation as given by Marshall Clagett:^[6]

"[...] equal weights at unequal distances do not weigh equally, but unequal weights [at these unequal distances may] weigh equally. For a weight suspended at a greater distance is heavier, as is obvious in a balance. Therefore, there exists a certain third kind of power or third difference of magnitude—one that differs from both body and weight—and this they call moment.^[13] Therefore, a body acquires weight from both quantity [i.e., size] and quality [i.e., material], but a weight receives its moment from the distance at which it is suspended. Therefore, when distances are reciprocally proportional to weights, the moments [of the weights] are equal, as Archimedes demonstrated in The Book on Equal Moments.^[14] Therefore, weights or [rather] moments like other continuous quantities, are joined at some common terminus, that is, at something common to both of them like the center of weight, or at a point of equilibrium. Now the center of gravity in any weight is that point which, no matter how often or whenever the body is suspended, always inclines perpendicularly toward the universal center.

In addition to body, weight, and moment, there is a certain fourth power, which can be called impetus or force.^[15] Aristotle investigates it in On Mechanical Questions, and it is completely different from [the] three aforesaid [powers or magnitudes]. [...]"

in 1586, Simon Stevin uses the Dutch term staltwicht ("parked weight") for momentum in De Beghinselen Der Weeghconst.

In 1632, Galileo Galilei publishes Dialogue Concerning the Two Chief World Systems and uses the Italian momento with many meanings, including the one of his predecessors.^[16]

In 1643, Thomas Salusbury translates some of Galilei's works into English. Salusbury translates Latin momentum and Italian momento into the English term moment.^[17]

In 1765, the Latin term momentum inertiae (English: moment of inertia) is used by Leonhard Euler to refer to one of Christiaan Huygens's quantities in Horologium Oscillatorium.^[18] Huygens 1673 work involving finding the center of oscillation had been stimulated by Marin Mersenne, who suggested it to him in 1646.^[19][20]

In 1811, the French term moment d'une force (English: moment of force) with respect to a point and plane is used by Siméon Denis Poisson in Traité de mécanique.^[21] An English translation appears in 1842.

In 1884, the term torque is suggested by James Thomson in the context of measuring rotational forces of machines (with propellers and rotors).^[22][23] Today, a dynamometer is used to measure the torque of machines.

In 1893, Karl Pearson uses the term n-th moment and [math]\displaystyle{ \mu_n }[/math] in the context of curve-fitting scientific measurements.^[24] Pearson wrote in response to John Venn, who, some years earlier, observed a peculiar pattern involving meteorological data and asked for an explanation of its cause.^[25] In Pearson's response, this analogy is used: the mechanical "center of gravity" is the mean and the "distance" is the deviation from the mean. This later evolved into moments in mathematics. The analogy between the mechanical concept of a moment and the statistical function involving the sum of the nth powers of deviations was noticed by several earlier, including Laplace, Kramp, Gauss, Encke, Czuber, Quetelet, and De Forest.^[26]