1. Formulation

In contrast to a Fourier series where the coefficients are fixed numbers and the expansion basis consists of sinusoidal functions (that is, sine and cosine functions), the coefficients in the Karhunen–Loève theorem are random variables and the expansion basis depends on the process. In fact, the orthogonal basis functions used in this representation are determined by the covariance function of the process. One can think that the Karhunen–Loève transform adapts to the process in order to produce the best possible basis for its expansion. In the case of a centered stochastic process {X_t}_t ∈ [a, b] (centered means E[X_t] = 0 for all t ∈ [a, b]) satisfying a technical continuity condition, X_t admits a decomposition

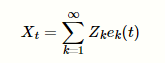
where Z_k are pairwise uncorrelated random variables and the functions ek are continuous real-valued functions on [a, b] that are pairwise orthogonal in L²([a, b]). It is therefore sometimes said that the expansion is bi-orthogonal since the random coefficients Z_k are orthogonal in the probability space while the deterministic functions ek are orthogonal in the time domain. The general case of a process X_t that is not centered can be brought back to the case of a centered process by considering X_t − E[X_t] which is a centered process. Moreover, if the process is Gaussian, then the random variables Z_k are Gaussian and stochastically independent. This result generalizes the Karhunen–Loève transform. An important example of a centered real stochastic process on [0, 1] is the Wiener process; the Karhunen–Loève theorem can be used to provide a canonical orthogonal representation for it. In this case the expansion consists of sinusoidal functions. The above expansion into uncorrelated random variables is also known as the Karhunen–Loève expansion or Karhunen–Loève decomposition. The empirical version (i.e., with the coefficients computed from a sample) is known as the Karhunen–Loève transform (KLT), principal component analysis, proper orthogonal decomposition (POD), empirical orthogonal functions (a term used in meteorology and geophysics), or the Hotelling transform.

• Throughout this article, we will consider a square-integrable zero-mean random process X_t defined over a probability space (Ω, F, P) and indexed over a closed interval [a, b], with covariance function K_X(s, t). We thus have:

[math]\displaystyle{ \forall t\in [a,b] \qquad X_t\in L^2(\Omega, F,\mathbf{P}), }[/math]

[math]\displaystyle{ \forall t\in [a,b] \qquad \mathbf{E}[X_t]=0, }[/math]

[math]\displaystyle{ \forall t,s \in [a,b] \qquad K_X(s,t)=\mathbf{E}[X_s X_t]. }[/math]

• We associate to K_X a linear operator T_KX defined in the following way:

[math]\displaystyle{ \begin{aligned} &T_{K_X}&: L^2([a,b]) &\to L^2([a,b])\\ &&: f \mapsto T_{K_X}f &= \int_a^b K_X(s,\cdot) f(s) \, ds \end{aligned} }[/math]

Since T_KX is a linear operator, it makes sense to talk about its eigenvalues λ_k and eigenfunctions e_k, which are found solving the homogeneous Fredholm integral equation of the second kind

[math]\displaystyle{ \int_a^b K_X(s,t) e_k(s)\,ds=\lambda_k e_k(t) }[/math]

2. Statement of the Theorem

Theorem. Let X_t be a zero-mean square-integrable stochastic process defined over a probability space (Ω, F, P) and indexed over a closed and bounded interval [a, b], with continuous covariance function K_X(s, t).

Then K_X(s,t) is a Mercer kernel and letting e_k be an orthonormal basis on L²([a, b]) formed by the eigenfunctions of T_KX with respective eigenvalues λ_k, X_t admits the following representation

[math]\displaystyle{ X_t=\sum_{k=1}^\infty Z_k e_k(t) }[/math]

where the convergence is in L², uniform in t and

[math]\displaystyle{ Z_k=\int_a^b X_t e_k(t)\, dt }[/math]

Furthermore, the random variables Z_k have zero-mean, are uncorrelated and have variance λ_k

[math]\displaystyle{ \mathbf{E}[Z_k]=0,~\forall k\in\mathbb{N} \qquad \mbox{and}\qquad \mathbf{E}[Z_i Z_j]=\delta_{ij} \lambda_j,~\forall i,j\in \mathbb{N} }[/math]

Note that by generalizations of Mercer's theorem we can replace the interval [a, b] with other compact spaces C and the Lebesgue measure on [a, b] with a Borel measure whose support is C.

3. Proof

• The covariance function K_X satisfies the definition of a Mercer kernel. By Mercer's theorem, there consequently exists a set λ_k, e_k(t) of eigenvalues and eigenfunctions of T_KX forming an orthonormal basis of L²([a,b]), and K_X can be expressed as

[math]\displaystyle{ K_X(s,t)=\sum_{k=1}^\infty \lambda_k e_k(s) e_k(t) }[/math]

• The process X_t can be expanded in terms of the eigenfunctions e_k as:

[math]\displaystyle{ X_t=\sum_{k=1}^\infty Z_k e_k(t) }[/math]

where the coefficients (random variables) Z_k are given by the projection of X_t on the respective eigenfunctions

[math]\displaystyle{ Z_k=\int_a^b X_t e_k(t) \,dt }[/math]

• We may then derive

[math]\displaystyle{ \begin{align} \mathbf{E}[Z_k] &=\mathbf{E}\left[\int_a^b X_t e_k(t) \,dt\right]=\int_a^b \mathbf{E}[X_t] e_k(t) dt=0 \\ [8pt] \mathbf{E}[Z_i Z_j]&=\mathbf{E}\left[ \int_a^b \int_a^b X_t X_s e_j(t)e_i(s)\, dt\, ds\right]\\ &=\int_a^b \int_a^b \mathbf{E}\left[X_t X_s\right] e_j(t)e_i(s) \, dt\, ds\\ &=\int_a^b \int_a^b K_X(s,t) e_j(t)e_i(s) \,dt \, ds\\ &=\int_a^b e_i(s)\left(\int_a^b K_X(s,t) e_j(t) \,dt\right) \, ds\\ &=\lambda_j \int_a^b e_i(s) e_j(s) \, ds\\ &=\delta_{ij}\lambda_j \end{align} }[/math]

where we have used the fact that the e_k are eigenfunctions of T_KX and are orthonormal.

• Let us now show that the convergence is in L². Let

[math]\displaystyle{ S_N=\sum_{k=1}^N Z_k e_k(t). }[/math]

Then:

[math]\displaystyle{ \begin{align} \mathbf{E} \left [\left |X_t-S_N \right |^2 \right ]&=\mathbf{E} \left [X_t^2 \right ]+\mathbf{E} \left [S_N^2 \right ] - 2\mathbf{E} \left [X_t S_N \right ]\\ &=K_X(t,t)+\mathbf{E}\left[\sum_{k=1}^N \sum_{l=1}^N Z_k Z_\ell e_k(t)e_\ell(t) \right] -2\mathbf{E}\left[X_t\sum_{k=1}^N Z_k e_k(t)\right]\\ &=K_X(t,t)+\sum_{k=1}^N \lambda_k e_k(t)^2 -2\mathbf{E}\left[\sum_{k=1}^N \int_a^b X_t X_s e_k(s) e_k(t) \,ds \right]\\ &=K_X(t,t)-\sum_{k=1}^N \lambda_k e_k(t)^2 \end{align} }[/math]

which goes to 0 by Mercer's theorem.

4. Properties of the Karhunen–Loève Transform

4.1. Special Case: Gaussian Distribution

Since the limit in the mean of jointly Gaussian random variables is jointly Gaussian, and jointly Gaussian random (centered) variables are independent if and only if they are orthogonal, we can also conclude:

Theorem. The variables Z_i have a joint Gaussian distribution and are stochastically independent if the original process {X_t}_t is Gaussian.

In the Gaussian case, since the variables Z_i are independent, we can say more:

[math]\displaystyle{ \lim_{N \to \infty} \sum_{i=1}^N e_i(t) Z_i(\omega) = X_t(\omega) }[/math]

almost surely.

4.2. The Karhunen–Loève Transform Decorrelates the Process

This is a consequence of the independence of the Z_k.

4.3. The Karhunen–Loève Expansion Minimizes the Total Mean Square Error

In the introduction, we mentioned that the truncated Karhunen–Loeve expansion was the best approximation of the original process in the sense that it reduces the total mean-square error resulting of its truncation. Because of this property, it is often said that the KL transform optimally compacts the energy.

More specifically, given any orthonormal basis {f_k} of L²([a, b]), we may decompose the process X_t as:

[math]\displaystyle{ X_t(\omega)=\sum_{k=1}^\infty A_k(\omega) f_k(t) }[/math]

where

[math]\displaystyle{ A_k(\omega)=\int_a^b X_t(\omega) f_k(t)\,dt }[/math]

and we may approximate X_t by the finite sum

[math]\displaystyle{ \hat{X}_t(\omega)=\sum_{k=1}^N A_k(\omega) f_k(t) }[/math]

for some integer N.

Claim. Of all such approximations, the KL approximation is the one that minimizes the total mean square error (provided we have arranged the eigenvalues in decreasing order).

4.4. Explained Variance

An important observation is that since the random coefficients Z_k of the KL expansion are uncorrelated, the Bienaymé formula asserts that the variance of X_t is simply the sum of the variances of the individual components of the sum:

[math]\displaystyle{ \operatorname{var}[X_t]=\sum_{k=0}^\infty e_k(t)^2 \operatorname{var}[Z_k]=\sum_{k=1}^\infty \lambda_k e_k(t)^2 }[/math]

Integrating over [a, b] and using the orthonormality of the e_k, we obtain that the total variance of the process is:

[math]\displaystyle{ \int_a^b \operatorname{var}[X_t] \, dt=\sum_{k=1}^\infty \lambda_k }[/math]

In particular, the total variance of the N-truncated approximation is

[math]\displaystyle{ \sum_{k=1}^N \lambda_k. }[/math]

As a result, the N-truncated expansion explains

[math]\displaystyle{ \frac{\sum_{k=1}^N \lambda_k}{\sum_{k=1}^\infty \lambda_k} }[/math]

of the variance; and if we are content with an approximation that explains, say, 95% of the variance, then we just have to determine an [math]\displaystyle{ N\in\mathbb{N} }[/math] such that

[math]\displaystyle{ \frac{\sum_{k=1}^N \lambda_k}{\sum_{k=1}^\infty \lambda_k} \geq 0.95. }[/math]

4.5. The Karhunen–Loève Expansion Has the Minimum Representation Entropy Property

Given a representation of [math]\displaystyle{ X_t=\sum_{k=1}^\infty W_k\varphi_k(t) }[/math], for some orthonormal basis [math]\displaystyle{ \varphi_k(t) }[/math] and random [math]\displaystyle{ W_k }[/math], we let [math]\displaystyle{ p_k=\mathbb{E}[|W_k|^2]/\mathbb{E}[|X_t|_{L^2}^2] }[/math], so that [math]\displaystyle{ \sum_{k=1}^\infty p_k=1 }[/math]. We may then define the representation entropy to be [math]\displaystyle{ H(\{\varphi_k\})=-\sum_i p_k \log(p_k) }[/math]. Then we have [math]\displaystyle{ H(\{\varphi_k\})\ge H(\{e_k\}) }[/math], for all choices of [math]\displaystyle{ \varphi_k }[/math]. That is, the KL-expansion has minimal representation entropy.

Proof:

Denote the coefficients obtained for the basis [math]\displaystyle{ e_k(t) }[/math] as [math]\displaystyle{ p_k }[/math], and for [math]\displaystyle{ \varphi_k(t) }[/math] as [math]\displaystyle{ q_k }[/math].

Choose [math]\displaystyle{ N\ge 1 }[/math]. Note that since [math]\displaystyle{ e_k }[/math] minimizes the mean squared error, we have that

[math]\displaystyle{ \mathbb{E} \left|\sum_{k=1}^N Z_ke_k(t)-X_t\right|_{L^2}^2\le \mathbb{E}\left|\sum_{k=1}^N W_k\varphi_k(t)-X_t\right|_{L^2}^2 }[/math]

Expanding the right hand size, we get:

[math]\displaystyle{ \mathbb{E}\left|\sum_{k=1}^N W_k\varphi_k(t)-X_t\right|_{L^2}^2 =\mathbb{E}|X_t^2|_{L^2} + \sum_{k=1}^N \sum_{\ell=1}^N \mathbb{E}[W_\ell \varphi_\ell(t)W_k^*\varphi_k^*(t)]_{L^2}-\sum_{k=1}^N \mathbb{E}[W_k \varphi_k X_t^*]_{L^2} - \sum_{k=1}^N \mathbb{E}[X_tW_k^*\varphi_k^*(t)]_{L^2} }[/math]

Using the orthonormality of [math]\displaystyle{ \varphi_k(t) }[/math], and expanding [math]\displaystyle{ X_t }[/math] in the [math]\displaystyle{ \varphi_k(t) }[/math] basis, we get that the right hand size is equal to:

[math]\displaystyle{ \mathbb{E}[X_t]^2_{L^2}-\sum_{k=1}^N\mathbb{E}[|W_k|^2] }[/math]

We may perform identical analysis for the [math]\displaystyle{ e_k(t) }[/math], and so rewrite the above inequality as:

[math]\displaystyle{ {\displaystyle \mathbb {E} [X_t]_{L^2}^2-\sum _{k=1}^N\mathbb {E} [|Z_k|^2]}\le {\displaystyle \mathbb {E} [X_t]_{L^2}^2-\sum _{k=1}^N\mathbb {E} [|W_k|^{2}]} }[/math]

Subtracting the common first term, and dividing by [math]\displaystyle{ \mathbb{E}[|X_t|^2_{L^2}] }[/math], we obtain that:

[math]\displaystyle{ \sum_{k=1}^N p_k\ge \sum_{k=1}^N q_k }[/math]

This implies that:

[math]\displaystyle{ -\sum_{k=1}^\infty p_k \log(p_k)\le -\sum_{k=1}^\infty q_k \log(q_k) }[/math]

5. Linear Karhunen–Loève Approximations

Consider a whole class of signals we want to approximate over the first M vectors of a basis. These signals are modeled as realizations of a random vector Y[n] of size N. To optimize the approximation we design a basis that minimizes the average approximation error. This section proves that optimal bases are Karhunen–Loeve bases that diagonalize the covariance matrix of Y. The random vector Y can be decomposed in an orthogonal basis

[math]\displaystyle{ \left\{ g_m \right\}_{0\le m\le N} }[/math]

as follows:

[math]\displaystyle{ Y=\sum_{m=0}^{N-1} \left\langle Y, g_m \right\rangle g_m, }[/math]

where each

[math]\displaystyle{ \left\langle Y, g_m \right\rangle =\sum_{n=0}^{N-1}{Y[n]} g_m^* [n] }[/math]

is a random variable. The approximation from the first M ≤ N vectors of the basis is

[math]\displaystyle{ Y_M=\sum_{m=0}^{M-1} \left\langle Y, g_m \right\rangle g_m }[/math]

The energy conservation in an orthogonal basis implies

[math]\displaystyle{ \varepsilon[M]= \mathbf{E} \left\{ \left\| Y- Y_M \right\|^2 \right\} =\sum_{m=M}^{N-1} \mathbf{E}\left\{ \left| \left\langle Y, g_m \right\rangle \right|^2 \right\} }[/math]

This error is related to the covariance of Y defined by

[math]\displaystyle{ R[ n,m]=\mathbf{E} \left\{ Y[n] Y^*[m] \right\} }[/math]

For any vector x[n] we denote by K the covariance operator represented by this matrix,

[math]\displaystyle{ \mathbf{E}\left\{\left|\langle Y,x \rangle\right|^2\right\}=\langle Kx,x \rangle =\sum_{n=0}^{N-1} \sum_{m=0}^{N-1} R[n,m]x[n]x^*[m] }[/math]

The error ε[M] is therefore a sum of the last N − M coefficients of the covariance operator

[math]\displaystyle{ \varepsilon [M]=\sum_{m=M}^{N-1}{\left\langle K g_m, g_m \right\rangle } }[/math]

The covariance operator K is Hermitian and Positive and is thus diagonalized in an orthogonal basis called a Karhunen–Loève basis. The following theorem states that a Karhunen–Loève basis is optimal for linear approximations.

Theorem (Optimality of Karhunen–Loève basis). Let K be a covariance operator. For all M ≥ 1, the approximation error

[math]\displaystyle{ \varepsilon [M]=\sum_{m=M}^{N-1}\left\langle K g_m, g_m \right\rangle }[/math]

is minimum if and only if

[math]\displaystyle{ \left\{ g_m \right\}_{0\le m\lt N} }[/math]

is a Karhunen–Loeve basis ordered by decreasing eigenvalues.

[math]\displaystyle{ \left\langle K g_m, g_m \right\rangle \ge \left\langle Kg_{m+1}, g_{m+1} \right\rangle, \qquad 0\le m\lt N-1. }[/math]

6. Non-Linear Approximation in Bases

Linear approximations project the signal on M vectors a priori. The approximation can be made more precise by choosing the M orthogonal vectors depending on the signal properties. This section analyzes the general performance of these non-linear approximations. A signal [math]\displaystyle{ f\in \Eta }[/math] is approximated with M vectors selected adaptively in an orthonormal basis for [math]\displaystyle{ \Eta }[/math]

[math]\displaystyle{ \Beta =\left\{ g_m \right\}_{m\in \mathbb{N}} }[/math]

Let [math]\displaystyle{ f_M }[/math] be the projection of f over M vectors whose indices are in I_M:

[math]\displaystyle{ f_M=\sum_{m\in I_M} \left\langle f, g_m \right\rangle g_m }[/math]

The approximation error is the sum of the remaining coefficients

[math]\displaystyle{ \varepsilon [M]=\left\{ \left\| f- f_M \right\|^2 \right\}=\sum_{m\notin I_M}^{N-1} \left\{ \left| \left\langle f, g_m \right\rangle \right|^2 \right\} }[/math]

To minimize this error, the indices in I_M must correspond to the M vectors having the largest inner product amplitude

[math]\displaystyle{ \left| \left\langle f, g_m \right\rangle \right|. }[/math]

These are the vectors that best correlate f. They can thus be interpreted as the main features of f. The resulting error is necessarily smaller than the error of a linear approximation which selects the M approximation vectors independently of f. Let us sort

[math]\displaystyle{ \left\{ \left| \left\langle f, g_m \right\rangle \right| \right\}_{m\in \mathbb{N}} }[/math]

in decreasing order

[math]\displaystyle{ \left| \left \langle f, g_{m_k} \right \rangle \right|\ge \left| \left \langle f, g_{m_{k+1}} \right \rangle \right|. }[/math]

The best non-linear approximation is

[math]\displaystyle{ f_M=\sum_{k=1}^M \left\langle f, g_{m_k} \right\rangle g_{m_k} }[/math]

It can also be written as inner product thresholding:

[math]\displaystyle{ f_M=\sum_{m=0}^\infty \theta_T \left( \left\langle f, g_m \right\rangle \right) g_m }[/math]

with

[math]\displaystyle{ T=\left|\left\langle f, g_{m_M} \right \rangle\right|, \qquad \theta_T(x)= \begin{cases} x & |x|\ge T \\ 0 & |x| \lt T \end{cases} }[/math]

The non-linear error is

[math]\displaystyle{ \varepsilon [M]=\left\{ \left\| f- f_M \right\|^2 \right\}=\sum_{k=M+1}^{\infty} \left\{ \left| \left\langle f, g_{m_k} \right\rangle \right|^2 \right\} }[/math]

this error goes quickly to zero as M increases, if the sorted values of [math]\displaystyle{ \left| \left\langle f, g_{m_k} \right\rangle \right| }[/math] have a fast decay as k increases. This decay is quantified by computing the [math]\displaystyle{ \Iota^\Rho }[/math] norm of the signal inner products in B:

[math]\displaystyle{ \| f \|_{\Beta, p} =\left( \sum_{m=0}^\infty \left| \left\langle f, g_m \right\rangle \right|^p \right)^{\frac{1}{p}} }[/math]

The following theorem relates the decay of ε[M] to [math]\displaystyle{ \| f\|_{\Beta, p} }[/math]

Theorem (decay of error). If [math]\displaystyle{ \| f\|_{\Beta ,p}\lt \infty }[/math] with p < 2 then

[math]\displaystyle{ \varepsilon [M]\le \frac{\|f\|_{\Beta ,p}^2}{\frac{2}{p}-1} M^{1-\frac{2}{p}} }[/math]

and

[math]\displaystyle{ \varepsilon [M]=o\left( M^{1-\frac{2}{p}} \right). }[/math]

Conversely, if [math]\displaystyle{ \varepsilon [M]=o\left( M^{1-\frac{2}{p}} \right) }[/math] then

[math]\displaystyle{ \| f\|_{\Beta ,q}\lt \infty }[/math] for any q > p.

6.1. Non-Optimality of Karhunen–Loève Bases

To further illustrate the differences between linear and non-linear approximations, we study the decomposition of a simple non-Gaussian random vector in a Karhunen–Loève basis. Processes whose realizations have a random translation are stationary. The Karhunen–Loève basis is then a Fourier basis and we study its performance. To simplify the analysis, consider a random vector Y[n] of size N that is random shift modulo N of a deterministic signal f[n] of zero mean

[math]\displaystyle{ \sum_{n=0}^{N-1}f[n]=0 }[/math]

[math]\displaystyle{ Y[n]=f [ (n-p)\bmod N ] }[/math]

The random shift P is uniformly distributed on [0, N − 1]:

[math]\displaystyle{ \Pr ( P=p )=\frac{1}{N}, \qquad 0\le p\lt N }[/math]

Clearly

[math]\displaystyle{ \mathbf{E}\{Y[n]\}=\frac{1}{N} \sum_{p=0}^{N-1} f[(n-p)\bmod N]=0 }[/math]

and

[math]\displaystyle{ R[n,k]=\mathbf{E} \{Y[n]Y[k] \}=\frac{1}{N}\sum_{p=0}^{N-1} f[(n-p)\bmod N] f [(k-p)\bmod N ] = \frac{1}{N} f\Theta \bar{f}[n-k], \quad \bar{f}[n]=f[-n] }[/math]

Hence

[math]\displaystyle{ R[n,k]=R_Y[n-k], \qquad R_Y[k]=\frac{1}{N}f \Theta \bar{f}[k] }[/math]

Since R_Y is N periodic, Y is a circular stationary random vector. The covariance operator is a circular convolution with R_Y and is therefore diagonalized in the discrete Fourier Karhunen–Loève basis

[math]\displaystyle{ \left\{ \frac{1}{\sqrt{N}} e^{i2\pi mn/N} \right\}_{0\le m\lt N}. }[/math]

The power spectrum is Fourier transform of R_Y:

[math]\displaystyle{ P_Y[m]=\hat{R}_Y[m]=\frac{1}{N} \left| \hat{f}[m] \right|^2 }[/math]

Example: Consider an extreme case where [math]\displaystyle{ f[n]=\delta [n]-\delta [n-1] }[/math]. A theorem stated above guarantees that the Fourier Karhunen–Loève basis produces a smaller expected approximation error than a canonical basis of Diracs [math]\displaystyle{ \left\{g_m[n]=\delta[n-m] \right\}_{0\le m\lt N} }[/math]. Indeed, we do not know a priori the abscissa of the non-zero coefficients of Y, so there is no particular Dirac that is better adapted to perform the approximation. But the Fourier vectors cover the whole support of Y and thus absorb a part of the signal energy.

[math]\displaystyle{ \mathbf{E} \left\{ \left| \left\langle Y[n],\frac{1}{\sqrt{N}} e^{i2\pi mn/N} \right\rangle \right|^2 \right\}=P_Y[m] = \frac{4}{N}\sin^2 \left(\frac{\pi k}{N} \right) }[/math]

Selecting higher frequency Fourier coefficients yields a better mean-square approximation than choosing a priori a few Dirac vectors to perform the approximation. The situation is totally different for non-linear approximations. If [math]\displaystyle{ f[n]=\delta[n]-\delta[n-1] }[/math] then the discrete Fourier basis is extremely inefficient because f and hence Y have an energy that is almost uniformly spread among all Fourier vectors. In contrast, since f has only two non-zero coefficients in the Dirac basis, a non-linear approximation of Y with M ≥ 2 gives zero error.^[1]

7. Principal Component Analysis

We have established the Karhunen–Loève theorem and derived a few properties thereof. We also noted that one hurdle in its application was the numerical cost of determining the eigenvalues and eigenfunctions of its covariance operator through the Fredholm integral equation of the second kind

[math]\displaystyle{ \int_a^b K_X(s,t) e_k(s)\,ds=\lambda_k e_k(t). }[/math]

However, when applied to a discrete and finite process [math]\displaystyle{ \left(X_n\right)_{n\in\{1,\ldots,N\}} }[/math], the problem takes a much simpler form and standard algebra can be used to carry out the calculations.

Note that a continuous process can also be sampled at N points in time in order to reduce the problem to a finite version.

We henceforth consider a random N-dimensional vector [math]\displaystyle{ X=\left(X_1~X_2~\ldots~X_N\right)^T }[/math]. As mentioned above, X could contain N samples of a signal but it can hold many more representations depending on the field of application. For instance it could be the answers to a survey or economic data in an econometrics analysis.

As in the continuous version, we assume that X is centered, otherwise we can let [math]\displaystyle{ X:=X-\mu_X }[/math] (where [math]\displaystyle{ \mu_X }[/math] is the mean vector of X) which is centered.

Let us adapt the procedure to the discrete case.

7.1. Covariance Matrix

Recall that the main implication and difficulty of the KL transformation is computing the eigenvectors of the linear operator associated to the covariance function, which are given by the solutions to the integral equation written above.

Define Σ, the covariance matrix of X, as an N × N matrix whose elements are given by:

[math]\displaystyle{ \Sigma_{ij}= \mathbf{E}[X_i X_j],\qquad \forall i,j \in \{1,\ldots,N\} }[/math]

Rewriting the above integral equation to suit the discrete case, we observe that it turns into:

[math]\displaystyle{ \sum_{j=1}^N \Sigma_{ij} e_j=\lambda e_i \quad \Leftrightarrow \quad \Sigma e=\lambda e }[/math]

where [math]\displaystyle{ e=(e_1~e_2~\ldots~e_N)^T }[/math] is an N-dimensional vector.

The integral equation thus reduces to a simple matrix eigenvalue problem, which explains why the PCA has such a broad domain of applications.

Since Σ is a positive definite symmetric matrix, it possesses a set of orthonormal eigenvectors forming a basis of [math]\displaystyle{ \R^N }[/math], and we write [math]\displaystyle{ \{\lambda_i,\varphi_i\}_{i\in\{1,\ldots,N\}} }[/math] this set of eigenvalues and corresponding eigenvectors, listed in decreasing values of λ_i. Let also Φ be the orthonormal matrix consisting of these eigenvectors:

[math]\displaystyle{ \begin{align} \Phi &:=\left(\varphi_1~\varphi_2~\ldots~\varphi_N\right)^T\\ \Phi^T \Phi &=I \end{align} }[/math]

7.2. Principal Component Transform

It remains to perform the actual KL transformation, called the principal component transform in this case. Recall that the transform was found by expanding the process with respect to the basis spanned by the eigenvectors of the covariance function. In this case, we hence have:

[math]\displaystyle{ X =\sum_{i=1}^N \langle \varphi_i,X\rangle \varphi_i =\sum_{i=1}^N \varphi_i^T X \varphi_i }[/math]

In a more compact form, the principal component transform of X is defined by:

[math]\displaystyle{ \begin{cases} Y=\Phi^T X \\ X=\Phi Y \end{cases} }[/math]

The i-th component of Y is [math]\displaystyle{ Y_i=\varphi_i^T X }[/math], the projection of X on [math]\displaystyle{ \varphi_i }[/math] and the inverse transform X = ΦY yields the expansion of X on the space spanned by the [math]\displaystyle{ \varphi_i }[/math]:

[math]\displaystyle{ X=\sum_{i=1}^N Y_i \varphi_i=\sum_{i=1}^N \langle \varphi_i,X\rangle \varphi_i }[/math]

As in the continuous case, we may reduce the dimensionality of the problem by truncating the sum at some [math]\displaystyle{ K\in\{1,\ldots,N\} }[/math] such that

[math]\displaystyle{ \frac{\sum_{i=1}^K \lambda_i}{\sum_{i=1}^N \lambda_i}\geq \alpha }[/math]

where α is the explained variance threshold we wish to set.

We can also reduce the dimensionality through the use of multilevel dominant eigenvector estimation (MDEE).^[2]

8. Examples

8.1. The Wiener Process

There are numerous equivalent characterizations of the Wiener process which is a mathematical formalization of Brownian motion. Here we regard it as the centered standard Gaussian process W_t with covariance function

[math]\displaystyle{ K_W(t,s) = \operatorname{cov}(W_t,W_s) = \min (s,t). }[/math]

We restrict the time domain to [a, b]=[0,1] without loss of generality.

The eigenvectors of the covariance kernel are easily determined. These are

[math]\displaystyle{ e_k(t) = \sqrt{2} \sin \left( \left(k - \tfrac{1}{2}\right) \pi t \right) }[/math]

and the corresponding eigenvalues are

[math]\displaystyle{ \lambda_k = \frac{1}{(k -\frac{1}{2})^2 \pi^2}. }[/math]

This gives the following representation of the Wiener process:

Theorem. There is a sequence {Z_i}_i of independent Gaussian random variables with mean zero and variance 1 such that

[math]\displaystyle{ W_t = \sqrt{2} \sum_{k=1}^\infty Z_k \frac{\sin \left(\left(k - \frac 1 2 \right) \pi t\right)}{ \left(k - \frac 1 2 \right) \pi}. }[/math]

Note that this representation is only valid for [math]\displaystyle{ t\in[0,1]. }[/math] On larger intervals, the increments are not independent. As stated in the theorem, convergence is in the L² norm and uniform in t.

8.2. The Brownian Bridge

Similarly the Brownian bridge [math]\displaystyle{ B_t=W_t-tW_1 }[/math] which is a stochastic process with covariance function

[math]\displaystyle{ K_B(t,s)=\min(t,s)-ts }[/math]

can be represented as the series

[math]\displaystyle{ B_t = \sum_{k=1}^\infty Z_k \frac{\sqrt{2} \sin(k \pi t)}{k \pi} }[/math]

9. Applications

Adaptive optics systems sometimes use K–L functions to reconstruct wave-front phase information (Dai 1996, JOSA A). Karhunen–Loève expansion is closely related to the Singular Value Decomposition. The latter has myriad applications in image processing, radar, seismology, and the like. If one has independent vector observations from a vector valued stochastic process then the left singular vectors are maximum likelihood estimates of the ensemble KL expansion.

9.1. Applications in Signal Estimation and Detection

Detection of a known continuous signal S(t)

In communication, we usually have to decide whether a signal from a noisy channel contains valuable information. The following hypothesis testing is used for detecting continuous signal s(t) from channel output X(t), N(t) is the channel noise, which is usually assumed zero mean Gaussian process with correlation function [math]\displaystyle{ R_N (t, s) = E[N(t)N(s)] }[/math]

[math]\displaystyle{ H: X(t) = N(t), }[/math]

[math]\displaystyle{ K: X(t) = N(t)+s(t), \quad t\in(0,T) }[/math]

Signal detection in white noise

When the channel noise is white, its correlation function is

[math]\displaystyle{ R_N(t) = \tfrac{1}{2} N_0 \delta (t), }[/math]

and it has constant power spectrum density. In physically practical channel, the noise power is finite, so:

[math]\displaystyle{ S_N(f) = \begin{cases} \frac{N_0}{2} &|f|\lt w \\ 0 & |f|\gt w \end{cases} }[/math]

Then the noise correlation function is sinc function with zeros at [math]\displaystyle{ \frac{n}{2\omega}, n \in \mathbf{Z}. }[/math] Since are uncorrelated and gaussian, they are independent. Thus we can take samples from X(t) with time spacing

[math]\displaystyle{ \Delta t = \frac{n}{2\omega} \text{ within } (0,''T''). }[/math]

Let [math]\displaystyle{ X_i = X(i\,\Delta t) }[/math]. We have a total of [math]\displaystyle{ n = \frac{T}{\Delta t} = T(2\omega) = 2\omega T }[/math] i.i.d observations [math]\displaystyle{ \{X_1, X_2,\ldots,X_n\} }[/math] to develop the likelihood-ratio test. Define signal [math]\displaystyle{ S_i = S(i\,\Delta t) }[/math], the problem becomes,

[math]\displaystyle{ H: X_i = N_i, }[/math]

[math]\displaystyle{ K: X_i = N_i + S_i, i = 1,2,\ldots,n. }[/math]

The log-likelihood ratio

[math]\displaystyle{ \mathcal{L}(\underline{x}) = \log\frac{\sum^n_{i=1} (2S_i x_i - S_i^2)}{2\sigma^2} \Leftrightarrow \Delta t \sum^n_{i = 1} S_i x_i = \sum^n_{i=1} S(i\,\Delta t)x(i\,\Delta t) \, \Delta t \gtrless \lambda_\cdot2 }[/math]

As t → 0, let:

[math]\displaystyle{ G = \int^T_0 S(t)x(t) \, dt. }[/math]

Then G is the test statistics and the Neyman–Pearson optimum detector is

[math]\displaystyle{ G(\underline{x}) \gt G_0 \Rightarrow K \lt G_0 \Rightarrow H. }[/math]

As G is Gaussian, we can characterize it by finding its mean and variances. Then we get

[math]\displaystyle{ H: G \sim N \left (0,\tfrac{1}{2}N_0E \right ) }[/math]

[math]\displaystyle{ K: G \sim N \left (E,\tfrac{1}{2}N_0E \right ) }[/math]

where

[math]\displaystyle{ \mathbf{E} = \int^T_0 S^2(t) \, dt }[/math]

is the signal energy.

The false alarm error

[math]\displaystyle{ \alpha = \int^\infty_{G_0} N \left (0, \tfrac{1}{2}N_0E \right) \, dG \Rightarrow G_0 = \sqrt{\tfrac{1}{2} N_0E} \Phi^{-1}(1-\alpha) }[/math]

And the probability of detection:

[math]\displaystyle{ \beta = \int^\infty_{G_0} N \left (E, \tfrac{1}{2}N_0E \right) \, dG = 1-\Phi \left (\frac{G_0 - E}{\sqrt{\tfrac{1}{2} N_0 E}} \right ) = \Phi \left (\sqrt{\frac{2E}{N_0}} - \Phi^{-1}(1-\alpha) \right ), }[/math]

where Φ is the cdf of standard normal, or Gaussian, variable.

Signal detection in colored noise

When N(t) is colored (correlated in time) Gaussian noise with zero mean and covariance function [math]\displaystyle{ R_N(t,s) = E[N(t)N(s)], }[/math] we cannot sample independent discrete observations by evenly spacing the time. Instead, we can use K–L expansion to uncorrelate the noise process and get independent Gaussian observation 'samples'. The K–L expansion of N(t):

[math]\displaystyle{ N(t) = \sum^{\infty}_{i=1} N_i \Phi_i(t), \quad 0\lt t\lt T, }[/math]

where [math]\displaystyle{ N_i =\int N(t)\Phi_i(t)\,dt }[/math] and the orthonormal bases [math]\displaystyle{ \{\Phi_i{t}\} }[/math] are generated by kernel [math]\displaystyle{ R_N(t,s) }[/math], i.e., solution to

[math]\displaystyle{ \int ^T_0 R_N(t,s)\Phi_i(s)\,ds = \lambda_i \Phi_i(t), \quad \operatorname{var}[N_i] = \lambda_i. }[/math]

Do the expansion:

[math]\displaystyle{ S(t) = \sum^{\infty}_{i = 1}S_i\Phi_i(t), }[/math]

where [math]\displaystyle{ S_i = \int^T _0 S(t)\Phi_i(t) \, dt }[/math], then

[math]\displaystyle{ X_i = \int^T _0 X(t)\Phi_i(t) \, dt = N_i }[/math]

under H and [math]\displaystyle{ N_i + S_i }[/math] under K. Let [math]\displaystyle{ \overline{X} = \{X_1,X_2,\dots\} }[/math], we have

[math]\displaystyle{ N_i }[/math] are independent Gaussian r.v's with variance [math]\displaystyle{ \lambda_i }[/math]

under H: [math]\displaystyle{ \{X_i\} }[/math] are independent Gaussian r.v's.

[math]\displaystyle{ f_H[x(t)|0\lt t\lt T] = f_H(\underline{x}) = \prod^\infty_{i=1} \frac{1}{\sqrt{2\pi \lambda_i}} \exp \left (-\frac{x_i^2}{2 \lambda_i} \right ) }[/math]

under K: [math]\displaystyle{ \{X_i - S_i\} }[/math] are independent Gaussian r.v's.

[math]\displaystyle{ f_K[x(t)\mid 0\lt t\lt T] = f_K(\underline{x}) = \prod^\infty_{i=1} \frac{1}{\sqrt{2\pi \lambda_i}} \exp \left(-\frac{(x_i - S_i)^2}{2 \lambda_i} \right) }[/math]

Hence, the log-LR is given by

[math]\displaystyle{ \mathcal{L}(\underline{x}) = \sum^{\infty}_{i=1} \frac{2S_i x_i - S_i^2}{2\lambda_i} }[/math]

and the optimum detector is

[math]\displaystyle{ G = \sum^\infty_{i=1} S_i x_i \lambda_i \gt G_0 \Rightarrow K, \lt G_0 \Rightarrow H. }[/math]

Define

[math]\displaystyle{ k(t) = \sum^\infty_{i=1} \lambda_i S_i \Phi_i(t), 0\lt t\lt T, }[/math]

then [math]\displaystyle{ G = \int^T _0 k(t)x(t)\,dt. }[/math]

How to find k(t)

Since

[math]\displaystyle{ \int^T_0 R_N(t,s)k(s) \, ds = \sum^\infty_{i=1} \lambda_i S_i \int^T _0 R_N(t,s)\Phi_i (s) \, ds = \sum^\infty_{i=1} S_i \Phi_i(t) = S(t), }[/math]

k(t) is the solution to

[math]\displaystyle{ \int^T_0 R_N(t,s)k(s)\,ds = S(t). }[/math]

If N(t)is wide-sense stationary,

[math]\displaystyle{ \int^T_0 R_N(t-s)k(s) \, ds = S(t), }[/math]

which is known as the Wiener–Hopf equation. The equation can be solved by taking fourier transform, but not practically realizable since infinite spectrum needs spatial factorization. A special case which is easy to calculate k(t) is white Gaussian noise.

[math]\displaystyle{ \int^T_0 \frac{N_0}{2}\delta(t-s)k(s) \, ds = S(t) \Rightarrow k(t) = C S(t), \quad 0\lt t\lt T. }[/math]

The corresponding impulse response is h(t) = k(T − t) = CS(T − t). Let C = 1, this is just the result we arrived at in previous section for detecting of signal in white noise.

Test threshold for Neyman–Pearson detector

Since X(t) is a Gaussian process,

[math]\displaystyle{ G = \int^T_0 k(t)x(t) \, dt, }[/math]

is a Gaussian random variable that can be characterized by its mean and variance.

[math]\displaystyle{ \begin{align} \mathbf{E}[G\mid H] &= \int^T_0 k(t)\mathbf{E}[x(t)\mid H]\,dt = 0 \\ \mathbf{E}[G\mid K] &= \int^T_0 k(t)\mathbf{E}[x(t)\mid K]\,dt = \int^T_0 k(t)S(t)\,dt \equiv \rho \\ \mathbf{E}[G^2\mid H] &= \int^T_0 \int^T_0 k(t)k(s) R_N(t,s)\,dt\,ds = \int^T_0 k(t) \left (\int^T_0 k(s)R_N(t,s) \, ds \right) = \int^T_0 k(t)S(t) \, dt = \rho \\ \operatorname{var}[G\mid H] &= \mathbf{E}[G^2\mid H] - (\mathbf{E}[G\mid H])^2 = \rho \\ \mathbf{E}[G^2\mid K] &=\int^T_0\int^T_0k(t)k(s) \mathbf{E}[x(t)x(s)]\,dt\,ds = \int^T_0\int^T_0k(t)k(s)(R_N(t,s) +S(t)S(s)) \, dt\, ds = \rho + \rho^2\\ \operatorname{var}[G\mid K] &= \mathbf{E}[G^2|K] - (\mathbf{E}[G|K])^2 = \rho + \rho^2 -\rho^2 = \rho \end{align} }[/math]

Hence, we obtain the distributions of H and K:

[math]\displaystyle{ H: G \sim N(0,\rho) }[/math]

[math]\displaystyle{ K: G \sim N(\rho, \rho) }[/math]

The false alarm error is

[math]\displaystyle{ \alpha = \int^\infty_{G_0} N(0,\rho)\,dG = 1 - \Phi \left (\frac{G_0}{\sqrt{\rho}} \right ). }[/math]

So the test threshold for the Neyman–Pearson optimum detector is

[math]\displaystyle{ G_0 = \sqrt{\rho} \Phi^{-1} (1-\alpha). }[/math]

Its power of detection is

[math]\displaystyle{ \beta = \int^\infty_{G_0} N(\rho, \rho) \, dG = \Phi \left (\sqrt{\rho} - \Phi^{-1}(1 - \alpha) \right) }[/math]

When the noise is white Gaussian process, the signal power is

[math]\displaystyle{ \rho = \int^T_0 k(t)S(t) \, dt = \int^T_0 S(t)^2 \, dt = E. }[/math]

Prewhitening

For some type of colored noise, a typical practise is to add a prewhitening filter before the matched filter to transform the colored noise into white noise. For example, N(t) is a wide-sense stationary colored noise with correlation function

[math]\displaystyle{ R_N(\tau) = \frac{B N_0}{4} e^{-B|\tau|} }[/math]

[math]\displaystyle{ S_N(f) = \frac{N_0}{2(1+(\frac{w}{B})^2)} }[/math]

The transfer function of prewhitening filter is

[math]\displaystyle{ H(f) = 1 + j \frac{w}{B}. }[/math]

Detection of a Gaussian random signal in Additive white Gaussian noise (AWGN)

When the signal we want to detect from the noisy channel is also random, for example, a white Gaussian process X(t), we can still implement K–L expansion to get independent sequence of observation. In this case, the detection problem is described as follows:

[math]\displaystyle{ H_0 : Y(t) = N(t) }[/math]

[math]\displaystyle{ H_1 : Y(t) = N(t) + X(t), \quad 0\lt t\lt T. }[/math]

X(t) is a random process with correlation function [math]\displaystyle{ R_X(t,s) = E\{X(t)X(s)\} }[/math]

The K–L expansion of X(t) is

[math]\displaystyle{ X(t) = \sum^\infty_{i=1} X_i \Phi_i(t), }[/math]

where

[math]\displaystyle{ X_i = \int^T_0 X(t)\Phi_i(t)\,dt }[/math]

and [math]\displaystyle{ \Phi_i(t) }[/math] are solutions to

[math]\displaystyle{ \int^T_0 R_X(t,s)\Phi_i(s)ds= \lambda_i \Phi_i(t). }[/math]

So [math]\displaystyle{ X_i }[/math]'s are independent sequence of r.v's with zero mean and variance [math]\displaystyle{ \lambda_i }[/math]. Expanding Y(t) and N(t) by [math]\displaystyle{ \Phi_i(t) }[/math], we get

[math]\displaystyle{ Y_i = \int^T_0 Y(t)\Phi_i(t) \, dt = \int^T_0 [N(t) + X(t)]\Phi_i(t) = N_i + X_i, }[/math]

where

[math]\displaystyle{ N_i = \int^T_0 N(t)\Phi_i(t)\,dt. }[/math]

As N(t) is Gaussian white noise, [math]\displaystyle{ N_i }[/math]'s are i.i.d sequence of r.v with zero mean and variance [math]\displaystyle{ \tfrac{1}{2}N_0 }[/math], then the problem is simplified as follows,

[math]\displaystyle{ H_0: Y_i = N_i }[/math]

[math]\displaystyle{ H_1: Y_i = N_i + X_i }[/math]

The Neyman–Pearson optimal test:

[math]\displaystyle{ \Lambda = \frac{f_Y\mid H_1}{f_Y\mid H_0} = Ce^{-\sum^\infty_{i=1} \frac{y_i^2}{2} \frac{\lambda_i}{\tfrac{1}{2} N_0 (\tfrac{1}{2}N_0 + \lambda_i)} }, }[/math]

so the log-likelihood ratio is

[math]\displaystyle{ \mathcal{L} = \ln(\Lambda) = K -\sum^\infty_{i=1}\tfrac{1}{2}y_i^2 \frac{\lambda_i}{\frac{N_0}{2} \left(\frac{N_0}{2} + \lambda_i\right)}. }[/math]

Since

[math]\displaystyle{ \widehat{X}_i = \frac{\lambda_i}{\frac{N_0}{2} \left( \frac{N_0}{2} + \lambda_i \right)} }[/math]

is just the minimum-mean-square estimate of [math]\displaystyle{ X_i }[/math] given [math]\displaystyle{ Y_i }[/math]'s,

[math]\displaystyle{ \mathcal{L} = K + \frac{1}{N_0} \sum^\infty_{i=1} Y_i \widehat{X}_i. }[/math]

K–L expansion has the following property: If

[math]\displaystyle{ f(t) = \sum f_i \Phi_i(t), g(t) = \sum g_i \Phi_i(t), }[/math]

where

[math]\displaystyle{ f_i = \int_0^T f(t) \Phi_i(t)\,dt, \quad g_i = \int_0^T g(t)\Phi_i(t) \, dt. }[/math]

then

[math]\displaystyle{ \sum^\infty_{i=1} f_i g_i = \int^T_0 g(t)f(t)\,dt. }[/math]

So let

[math]\displaystyle{ \widehat{X}(t\mid T) = \sum^\infty_{i=1} \widehat{X}_i \Phi_i(t), \quad \mathcal{L} = K + \frac{1}{N_0} \int^T_0 Y(t) \widehat{X}(t\mid T) \, dt. }[/math]

Noncausal filter Q(t,s) can be used to get the estimate through

[math]\displaystyle{ \widehat{X}(t\mid T) = \int^T_0 Q(t,s)Y(s)\,ds. }[/math]

By orthogonality principle, Q(t,s) satisfies

[math]\displaystyle{ \int^T_0 Q(t,s)R_X(s,t)\,ds + \tfrac{N_0}{2} Q(t, \lambda) = R_X(t, \lambda), 0 \lt \lambda \lt T, 0\lt t\lt T. }[/math]

However, for practical reasons, it's necessary to further derive the causal filter h(t,s), where h(t,s) = 0 for s > t, to get estimate [math]\displaystyle{ \widehat{X}(t\mid t) }[/math]. Specifically,

[math]\displaystyle{ Q(t,s) = h(t,s) + h(s, t) - \int^T_0 h(\lambda, t)h(s, \lambda) \, d\lambda }[/math]