
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Beatrix Zheng | -- | 2739 | 2022-11-03 01:39:12 |
Video Upload Options
A Discrete Global Grid (DGG) is a mosaic which covers the entire Earth's surface. Mathematically it is a space partitioning: it consists of a set of non-empty regions that form a partition of the Earth’s surface. In a usual grid-modeling strategy, to simplify position calculations, each region is represented by a point, abstracting the grid as a set of region-points. Each region or region-point in the grid is called a cell. When each cell of a grid is subject to a recursive partition, resulting in a "series of discrete global grids with progressively finer resolution", forming a hierarchical grid, it is named Hierarchical DGG (sometimes "DGG system"). Discrete Global Grids are used as the geometric basis for the building of geospatial data structures. Each cell is related with data objects or values, or (in the hierarchical case) may be associated with other cells. DGGs have been proposed for use in a wide range of geospatial applications, including vector and raster location representation, data fusion, and spatial databases. The most usual grids are for horizontal position representation, using a standard datum, like WGS84. In this context is commom also to use a specific DGG as foundation for geocoding standardization. In the context of a spatial index, a DGG can assign unique identifiers to each grid cell, using it for spatial indexing purposes, in geodatabases or for geocoding.
1. Reference Model of the Globe
The "globe", in the DGG concept, have no strict semantic; but in Geodesy a so-called "Grid Reference System" is a grid that divides space with precise positions relative to a datum, that is an approximated a "standard model of the Geoid". So, in the role of Geoid, the "globe" coverd by a DGG can be any of the following objects:
- The topographical surface of the Earth, when each cell of the grid have its surface-position coordinates and the elevantion in relation to the standard Geoid. Example: grid with coordinates (φ,λ,z) where z is the elevation.
- A standard Geoid surface. The z coordinate is zero for all grid, them can be omitted, (φ,λ).
Ancient standards, before 1687 (the Newton's Principia publication), used a "reference sphere"; in nowadays the Geoid is mathematically abstracted as reference ellipsoid.- A simplified Geoid: sometimes an old geodesic standard (eg. SAD69) or a non-geodesic surface (e. g. perfectly spherical surface) must be adopted, and will covered by the grid. In this case cells must be labeled with non-ambiguous way, (φ',λ'), and the transformation (φ,λ)⟾(φ',λ') must be known.
- A projection surface. Typically the geographic coordinates (φ,λ) are projected (with some distortion) onto the 2D mapping plane with 2D Cartesian coordinates (x, y).
As a global modeling process, modern DGGs, when including projection process, tend to avoid surfaces like cylinder or a conic solids that result in discontinuities and indexing problems. Regular polyhedra and other topological equivalents of sphere led to the most promising known options to be covered by DGGs,[1] because "spherical projections preserve the correct topology of the Earth – there are no singularities or discontinuities to deal with"[2].
When working with a DGG it is important to specify which of these options was adopted. So, the characterization of the reference model of the globe of a DGG can be summarized by:
- The recovered object: the object type in the role of globe. If there are no projection, the object covered by the grid is the Geoid, the Earth or a sphere; else is the geometry class of the projection surface (e.g. a cylinder, a cube or a cone).
- Projection type: absent (no projection) or present. When present, its characterization can be summarized by the projection's goal property (e.g. equal-area, conformal, etc.) and the class of the corrective function (e.g. trigonometric, linear, quadractic, etc.).
NOTE: when the DGG is covering a projection surface, in a context of data provenance, the metadata about reference-Goid is also important — typical informing its ISO 19111's CRS value, with no confusion with the projection surface.
2. Types and Examples
The main distinguishing feature to classify or compare DGGs is the use or not of an hierarchical grid structures:
- In hierarchical reference systems each cell is a "box reference" to a subset of cells, and cell identifiers can express this hierarchy in its numbering logic or structure.
- In non-hierarchical reference systems each cell have a distinc identifier and represents a fixed-scale region of the space. The discretization of the Latitude/Longitude system is the most popular, and the standard reference for conversions.
Other usual criteria to classify a DGG are tile-shape and granularity (grid resolution):
- Tile regularity and shape: there are regular, semi-regular or irregular grid. As in generic tilings by regular polygons, is possible to tiling with regular face (like wall tiles can be rectangular, triangular, hexagonal, etc.), or with same face type but changing its size or angles, resulting in semi-regular shapes.
Uniformity of shape and regularity of metrics provide better grid-indexing algorithms. Although it has less practical use, totally irregular grids are possible, such in a Voronoi coverage.
- Fine or coarse granulation (cell size): modern DGGs are parametrizable in its grid resolution, so, it is a characteristic of the final DGG instance, but not usefull to classify DGGs, except when the DGG-type must use an specific resolution or have a discretization limit. A "fine" granulation grid is non-limited and "coarse" refers to drastic limitation. Historically the main limitations are related to digital/analogic media, the compression/expanded representations of the grid in a database, and the memory limitations to store the grid. When a quantitative characterization is necessary, the average area of the grid cells or average distance between cell centers can be adopted.
2.1. Non-Hierarchical Grids
The most common class of Discrete Global Grids are those that place cell center points on longitude/latitude meridians and parallels, or which use the longitude/latitude meridians and parallels to form the boundaries of rectangular cells. Examples of such grids, all based on Latitude/Longitude:
2.2. Hierarchical Grids
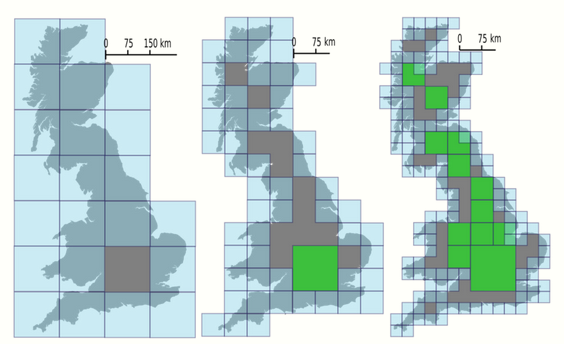
The right aside illustration show 3 boundary maps of the coast of Great Britain. The first map was covered by a grid-level-0 with 150 km size cells. Only a grey cell in the center, with no need of zoom for detail, remains level-0; all other cells of the second map was partitioned into four-cells-grid (grid-level-1), each with 75 km. In the third map 12 cells level-1 remains as grey, all other was partitioned again, each level-1-cell transformed into a level-2-grid.
3. Database Modeling
thumb|520px|In all DGG databases the grid is a [[Class diagram#Composition|composition of its cells. The region and centralPoint are illustrated as typical properties or subclasses. The cell identifier (cell ID) is also an important property, used as internal index and/or as public label of the cell (instead the point-coordinates) in geocoding applications. Sometimes, as in the MGRS grid, the coordinates make the role of ID.]]
There are many DGGs because there are many representational, optimization and modeling alternatives. All DGG grid is a composition of its cells, and, in the Hierarchical DGG each cell use a new grid over its local region.
The illustration is not adequate to TIN DEM cases and similar "raw data" structures, where the database not use the cell concept (that geometrically is the triangular region), but nodes and edges: each node is an elevation and each edge is the distance between to nodes.
In general each cell of the DGG is identified by the coordinates of its region-point (illustrated as the centralPoint of a database representation). It is also possible, with loss of functionality, to use a "free identifier", that is, any unique number or unique symbolic label per cell, the cell ID. The ID is usually used as spatial index (such as internal Quadtree or k-d tree), but is also possible to transform ID into a human-readable label for geocoding applications.
Modern databases (e.g. using S2 grid) use also multiple representations for the same data, offering both, a grid (or cell region) based in the Geoid and a grid based in the projection.
4. History
Discrete Global Grids with cell regions defined by parallels and meridians of latitude/longitude have been used since the earliest days of global geospatial computing. Before it, the discretization of continuous coordinates for practical purposes, with paper maps, occurred only with low granularity. Perhaps the most representative and main example of DGG of this pre-digital era was the 1940's military UTM DGGs, with finner granulaed cell identification for geocoding purposes. Similarly some hierarchical grid exists before geospatial computing, but only in coarse granulation.
A global surface is not required for use on daily geographical maps, and the memory was very expansive before the 2000s, to put all planetary data into the same computer. The first digital global grids was used for data processing of the satellite images and global (climatic and oceanographic) fluid dynamics modeling.
The first published references to Hierarchical Geodesic DGG systems are to systems developed for atmospheric modeling and published in 1968. These systems have hexagonal cell regions created on the surface of a spherical icosahedron. [3] [4]
The spatial hierarchical grids was subject to more intensive studies in the 1980's [5], when main structures, as Quadtree, was adapted in image indexing and databases.
While specific instances of these grids have been in use for decades, the term Discrete Global Grids were coined by researchers at Oregon State University in 1997[6] to describe the class of all such entities.
4.1. Comparison and Evolution
The evaluation Discrete Global Grid consists of many aspects, including area, shape, compactness, etc. Evaluation methods for map projection, such as Tissot's indicatrix, are also suitable for evaluating map projection based Discrete Global Grid.

In addition, averaged ratio between complementary profiles (AveRaComp) [7] gives a good evaluation of shape distortions for quadrilateral-shaped Discrete Global Grid.
Database development-choices and adaptations are oriented by practical demands, for greater performance, reliability or precision. The best choices are being selected and adapted to necessities, propitiating the evolution of the DGG architectures. Examples of this evolution process: from non-hierarchical to hierarchical DGGs; from the use of Z-curve indexes (a naive algorithm based in digits-interlacing), used by Geohash, to Hilbert-curve indexes, used in modern optimizations, like S2.
5. Geocoding Variants
In general each cell of the grid is identified by the coordinates of its region-point, but it is also possible to simplify the coordinate syntax and semantics, to obtain a identifier, as in a classic alphanumeric grids — and find the coordinates of a region-point from its identifier. Small and fast coordinate representations is a goal in the cell-ID implementations, for any DGG solutions.
There are no loss of functionality when using a "free identifier" instead a coodinate, that is, any unique number or unique symbolic label per region-point, the cell ID. So, to transform a coordinate into a human-readable label, and/or compressing the length of the label, is an additional step in the grid repesentation.
Some popular "global place codes" as ISO 3166-1 alpha-2 for administrative regions or Longhurst code for ecological regions of the globe, are partial in globe's coverage. By other hand, any set of cell-identifiers of a specific DGG can be used as "full-coverage place codes". Each different set of IDs, when used as a standard for data interchange purposes, are named "geocoding system".
There are many ways to represent the value of a cell identifier (cell-ID) of a grid: structured or monolithic, binary or not, human-readable or not. Supposing a map feature, like the Singapore's Merlion fountaine (~5m scale feature), represented by its minimum bounding cell or a center-point-cell, the cell ID will be:
| Cell ID | DGG variant name and parameters | ID structure; grid resolution |
|---|---|---|
| (1° 17′ 13.28″ N, 103° 51′ 16.88″ E) | ISO 6709/D in Degrees (Annex ), CRS=WGS84 | lat(deg min sec dir) long(deg min sec dir); seconds with 2 fractionary places |
| (1.286795, 103.854511) | ISO 6709/F in decimal and CRS=WGS84 | (lat,long); 6 fractionary places |
| (1.65AJ, 2V.IBCF) | ISO 6709/F in decimal in base36 (non-ISO) and CRS=WGS84 | (lat,long); 4 fractionary places |
| w21z76281 | Geohash, base32, WGS84 | monolithic; 9 characteres |
| 6PH57VP3+PR | PlusCode, base20, WGS84 | monolithic; 10 characteres |
| 48N 372579 142283 | UTM, satandard decimal, WGS84 | zone lat long; 3 + 6 + 6 digits |
| 48N 7ZHF 31SB | UTM, coordinates base36, WGS84 | zone lat long; 3 + 4 + 4 digits |
All these geocodes represents the same position in the globe, with similar precision, but differ in string-length, separators-use and alphabet (non-separator characters). In some cases the "original DGG" representation can be used. The variants are minor changes, affecting only final representation, for example the base of the numeric representation, or interlacing parts of the structured into only one number or code representation. The most popular variants are used for geocoding applications.
5.1. Alphanumeric Global Grids
DGGs and its variants, with human-readable cell-identifiers, has been used as de facto standard for alphanumeric grids. It is not limited to alphanumeric symbols, but "alphanumeric" is the most usual term.
Geocodes are notations for locations, and in a DGG context, notations to express grid cell IDs. There are a continuous evolution in digital standards and DGGs, so a continuous change in the popularity of each geocoding covention in the last years. Broader adoption also depends on country's government adoption, use in popular mapping platforms, and many other factors.
Examples used in the following list are about "minor grid cell" containing the Washington obelisk, 38° 53′ 22.11″ N, 77° 2′ 6.88″ W.
| DGG name/var | Inception and license | Summary of variant | Description and example |
|---|---|---|---|
| UTM zones/non-overlaped | 1940s - CC0 | original without overlaping | Divides the Earth into sixty polygonal strips. Example: 18S |
| Discrete UTM | 1940s - CC0 | original UTM integers | Divides the Earth into sixty zones, each being a six-degree band of longitude, and uses a secant transverse Mercator projection in each zone. No information about first digital use and conentions. Supposed that standardizations was later ISO's (1980s). Example: 18S 323483 4306480 |
| ISO 6709 | 1983 - CC0 | original degree representation | The grid resolutions is a function of the number of digits — with leading zeroes filled when necessary, and fractional part with appropriate number of digits to represent the required precision of the grid. Example: 38° 53′ 22.11″ N, 77° 2′ 6.88″ W. |
| ISO 6709 | 1983 - CC0 | 7 decimal digits representation | Variant based in the XML representation where the data structure is a "tuple consisting of latitude and longitude represents 2-dimensional geographic position", and each number in the tuple is a real number discretized with 7 decimal places. Example: 38.889475, -77.035244. |
| Mapcode | 2001 - patented | original | The first to adopt a mix code, in conjunction with ISO 3166's codes (country or city). In 2001 the algorithms was licensed Apache2, but all system remains patented. |
| Geohash | 2008 - CC0 | original | Is like a bit-enterlaced latLong, and the result is represented with base20. |
| Geohash | 2011 - CC0 | Base36, also named Geohash-36 | Only changes the base32 to base36, resulting in a little bit compressed code tham original Geohash. |
| What3words | 2013 patented | original (english) | converts 3x3 meter squares into 3 English-dictionary words.[8] |
| PlusCode | 2014 - Apache2[9] | original | Also named "Open Location Code". Codes are base20 numbers, and can use city-names, reducing code by the size of the city's bounding box code (like Mapcode strategy). Example: 87C4VXQ7+QV. |
| S2 Cell ID/Base32 | 2015 - Apache2[10] | original 64-bit integer expressed as base32 | Hierarchical and very effective database indexing, but no standard representation for base32 and city-prefixes, as PlusCode. |
| What3words/otherLang | 2016 ... 2017 - patented | other languages | same as English, but using other dictionary as reference for words. Portuguese example, and 10x14m cell: tenaz.fatual.davam. |
Other documented variants, but supposed not in use, or to be "never popular":
| DGG name | Inception - license | Summary | Description |
|---|---|---|---|
| C-squares | 2003 - "no restriction" | Latlong interlaced | Decimal-interlacing of ISO LatLong-degree representation. It is a "Naive" algorithm when compared with binary-interlacing or Geohash. |
| GEOREF | ~1990 - CC0 | Based on the ISO LatLong, but uses a simpler and more concise notation | "World Geographic Reference System", a military / air navigation coordinate system for point and area identification. |
| Geotude | ? | ? | ? |
| GARS | 2007 - restricted | USA/NGA | Reference system developed by the National Geospatial-Intelligence Agency (NGA). "the standardized battlespace area reference system across DoD which will impact the entire spectrum of battlespace deconfliction" |
| WMO squares | 2001.. - CC0? | specialiezed | NOAA's image download cells. ... divides a chart of the world with latitude-longitude gridlines into grid cells of 10° latitude by 10° longitude, each with a unique, 4-digit numeric identifier. 36x18 rectangular cells (labeled by four digits, the first digit indentify quadrants NE/SE/SW/NW). |
References
- Sahr, Kevin; White, Denis; Kimerling, A.J. (2003). "Geodesic discrete global grid systems". Cartography and Geographic Information Science 30 (2): 121–134. doi:10.1559/152304003100011090. http://webpages.sou.edu/~sahrk/sqspc/pubs/gdggs03.pdf.
- http://s2geometry.io/about/overview
- 2.0.co;2. https://dx.doi.org/10.1175%2F1520-0493%281968%29096%3C0351%3Aiotnbv%3E2.0.co%3B2" id="ref_3">Sadourny, R.; Arakawa, A.; Mintz, Y. (1968). "Integration of the nondivergent barotropic vorticity equation with an icosahedral-hexagonal grid for the sphere". Monthly Weather Review 96 (6): 351–356. doi:10.1175/1520-0493(1968)096<0351:iotnbv>2.0.co;2. https://dx.doi.org/10.1175%2F1520-0493%281968%29096%3C0351%3Aiotnbv%3E2.0.co%3B2
- Williamson, D.L. (1968). "Integration of the barotropic vorticity equation on a spherical geodesic grid.". Tellus 20 (4): 642–653. doi:10.1111/j.2153-3490.1968.tb00406.x. https://dx.doi.org/10.1111%2Fj.2153-3490.1968.tb00406.x
- https://pdfs.semanticscholar.org/edaa/8fc5e196791c821a5c81e987e2f5ca3c6aa5.pdf
- Sahr, Kevin; White, Denis; Kimerling, A.J. (18 March 1997), "A Proposed Criteria for Evaluating Discrete Global Grids", Draft Technical Report (Corvallis, Oregon: Oregon State University), http://bufo.geo.orst.edu/tc/firma/gg/criteria/criteria.toc.html
- Yan, Jin; Song, Xiao; Gong, Guanghong (2016). "Averaged ratio between complementary profiles for evaluating shape distortions of map projections and spherical hierarchical tessellations". Computers & Geosciences 87: 41–55. doi:10.1016/j.cageo.2015.11.009. http://www.sciencedirect.com/science/article/pii/S0098300415300868. Retrieved 2015-11-27.
- "What3words: Find and share very precise locations via Google Maps with just 3 words". https://thenextweb.com/apps/2013/07/02/what3words-a-new-way-to-search-for-and-share-locations-via-google-maps-with-just-3-words-universal-address-system/. Retrieved 8 July 2014.
- https://github.com/google/open-location-code
- https://github.com/google/s2geometry




