
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Rita Xu | -- | 2919 | 2022-11-02 01:34:18 |
Video Upload Options
In functional analysis and related areas of mathematics, group algebras are constructions that generalize the concept of group ring to some classes of topological groups with the aim to reduce the theory of representations of topological groups to the theory of representations of topological algebras. There are several nonequivalent definitions of group algebra, each of which is considered convenient in a particular situation.
1. Idea: Group Algebras for Finite Groups
If [math]\displaystyle{ G }[/math] is a finite group then for any field [math]\displaystyle{ K }[/math] the set [math]\displaystyle{ K^G }[/math] of all functions [math]\displaystyle{ u:G\to K }[/math] possesses a natural structure of (finite-dimensional) Hopf algebra over [math]\displaystyle{ K }[/math] with (the usual pointwise summation of functions and multiplication them by scalars, and)
- the multiplication [math]\displaystyle{ \nabla:K^G\otimes K^G\to K^G }[/math], generated by the pointwise multiplication of functions,
- [math]\displaystyle{ \nabla(u\otimes v)(t)=u(t)\cdot v(t),\quad u,v\in K^G, \quad t\in G, }[/math]
- the comultiplication [math]\displaystyle{ \Delta:K^G\to K^{G\times G}\cong K^G\otimes K^G }[/math], generated by the operation of multiplication in [math]\displaystyle{ G }[/math]
- [math]\displaystyle{ \Delta(u)(s,t)=u(s\cdot t),\quad u\in K^G, \quad s,t\in K, }[/math]
- and the antipode [math]\displaystyle{ S:K^G\to K^G }[/math] generated by the operation of taking the inverse element in [math]\displaystyle{ G }[/math]
- [math]\displaystyle{ S(u)(t)=u(t^{-1}),\quad u\in K^G, \quad t\in K. }[/math]
The dual space [math]\displaystyle{ K_G=(K^G)' }[/math] (of all linear functionals [math]\displaystyle{ \alpha:K^G\to K }[/math]) is the dual Hopf algebra, where, in particular, the multiplication [math]\displaystyle{ (\alpha,\beta)\in K_G\times K_G\mapsto \alpha*\beta \in K_G }[/math] can be described by the formula
[math]\displaystyle{ \alpha*\beta(u)=\sum_{s,t\in G}\alpha_s\cdot\beta_t\cdot u(s\cdot t),\quad u\in K^G, }[/math]
or by the formula
[math]\displaystyle{ \alpha*\beta=\sum_{s,t\in G} \alpha_s\cdot\beta_t\cdot\delta_{s\cdot t}, }[/math]
where
[math]\displaystyle{ \delta_t\in K_G, \quad \delta_t(u)=u(t),\quad u\in K^G,\quad t\in G }[/math]
are delta-functionals, and
[math]\displaystyle{ \alpha=\sum_{s\in G} \alpha_s\cdot\delta_s,\quad \beta=\sum_{t\in G} \beta_t\cdot\delta_t }[/math]
are the expansions of [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] along the basis [math]\displaystyle{ \{\delta_t;\ t\in G\} }[/math] in the vector space [math]\displaystyle{ K_G }[/math].
- The algebra [math]\displaystyle{ K_G }[/math] (denoted also as [math]\displaystyle{ K[G] }[/math]) is called the group algebra (or the group ring) of the group [math]\displaystyle{ G }[/math] over the field [math]\displaystyle{ K }[/math].
- A map [math]\displaystyle{ \pi:G\to A }[/math] of a group [math]\displaystyle{ G }[/math] into a unital associative algebra [math]\displaystyle{ A }[/math] over [math]\displaystyle{ K }[/math] is called a representation of the group [math]\displaystyle{ G }[/math] in the algebra [math]\displaystyle{ A }[/math], if it preserves the unit and the multiplication:
- [math]\displaystyle{ \pi(1_G)=1_A,\quad \pi(s\cdot t)=\pi(s)\cdot\pi(t),\quad s,t\in G. }[/math]
Example: the operation of passage to the delta-functional
[math]\displaystyle{ \delta:G\to K_G,\quad t\in G\mapsto \delta_t\in K_G }[/math]
is a representation of [math]\displaystyle{ G }[/math] in [math]\displaystyle{ K_G }[/math]:
[math]\displaystyle{ \delta_{1_G}=1_{K_G},\quad \delta_{s\cdot t}=\delta_s*\delta_t,\quad s,t\in G. }[/math]
There is a natural correspondence between the representations of the group [math]\displaystyle{ G }[/math] in (unital associative) algebras [math]\displaystyle{ A }[/math] and the homomorphisms of the unital algebras [math]\displaystyle{ \varphi:K_G\to A }[/math]:
- Theorem (universal property).
For any finite group [math]\displaystyle{ G }[/math] and for any unital associative algebra [math]\displaystyle{ A }[/math] over [math]\displaystyle{ K }[/math] the formula
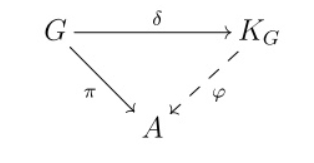 Universal property of group algebra. https://handwiki.org/wiki/index.php?curid=1370832
Universal property of group algebra. https://handwiki.org/wiki/index.php?curid=1370832
- [math]\displaystyle{ \pi=\varphi\circ\delta }[/math]
- establishes a one-to-one correspondence between the representations [math]\displaystyle{ \pi:G\to A }[/math] of the group [math]\displaystyle{ G }[/math] in [math]\displaystyle{ A }[/math] and the homomorphisms of the unital associative algebras [math]\displaystyle{ \varphi:K_G\to A }[/math].
This observation has a series of important corollaries, which allow to reduce the theory of representations of finite groups to the theory of representations of finite-dimensional algebras[1][2].
The construction of the group algebra [math]\displaystyle{ K_G }[/math] can be easily generalized to arbitrary (not necessarily finite) groups [math]\displaystyle{ G }[/math] (in the purely algebraic sense, without topology) with the same purposes: the generalization is called group ring [math]\displaystyle{ K[G] }[/math], and many results are preserved in this way, including the fact that [math]\displaystyle{ K[G] }[/math] possesses the universal property (and is a Hopf algebra when [math]\displaystyle{ K }[/math] is a field). But up to the recent time the generalizations to the topological groups faced numerous difficulties because of the lack of the convenient categories of topological vector spaces with dualities. The generalizations were mostly constructed in the category of Banach spaces, but the absence of a suitable duality in this category led to various distortions of the properties of these constructions, in particular, they were not Hopf algebras, and even the correspondence between the representations of groups and the homomorphisms of their group algebras was usually violated (however, this correspondence sometimes could be understood in some special sense).
2. Classical Group Algebras in Functional Analysis
In classical functional analysis, there are several constructions generalizing the purely algebraic idea of group algebra, but preserving only some part of its main properties.
2.1. The algebra Cc(G) of Continuous Functions with Compact Support
If G is a locally compact Hausdorff group, G carries an essentially unique left-invariant countably additive Borel measure μ called a Haar measure. Using the Haar measure, one can define a convolution operation on the space Cc(G) of complex-valued continuous functions on G with compact support; Cc(G) can then be given any of various norms and the completion will be a group algebra.
To define the convolution operation, let f and g be two functions in Cc(G). For t in G, define
- [math]\displaystyle{ [f * g](t) = \int_G f(s) g \left (s^{-1} t \right )\, d \mu(s). }[/math]
The fact that f * g is continuous is immediate from the dominated convergence theorem. Also
- [math]\displaystyle{ \operatorname{Support}(f * g) \subseteq \operatorname{Support}(f) \cdot \operatorname{Support}(g) }[/math]
where the dot stands for the product in G. Cc(G) also has a natural involution defined by:
- [math]\displaystyle{ f^*(s) = \overline{f(s^{-1})} \, \Delta(s^{-1}) }[/math]
where Δ is the modular function on G. With this involution, it is a *-algebra.
Theorem. With the norm:
- [math]\displaystyle{ \|f\|_1 := \int_G |f(s)| \, d\mu(s), }[/math]
Cc(G) becomes an involutive normed algebra with an approximate identity.
The approximate identity can be indexed on a neighborhood basis of the identity consisting of compact sets. Indeed, if V is a compact neighborhood of the identity, let fV be a non-negative continuous function supported in V such that
- [math]\displaystyle{ \int_V f_{V}(g)\, d \mu(g) =1. }[/math]
Then {fV}V is an approximate identity. A group algebra has an identity, as opposed to just an approximate identity, if and only if the topology on the group is the discrete topology.
Note that for discrete groups, Cc(G) is the same thing as the complex group ring C[G].
The importance of the group algebra is that it captures the unitary representation theory of G as shown in the following
Theorem. Let G be a locally compact group. If U is a strongly continuous unitary representation of G on a Hilbert space H, then
- [math]\displaystyle{ \pi_U (f) = \int_G f(g) U(g)\, d \mu(g) }[/math]
is a non-degenerate bounded *-representation of the normed algebra Cc(G). The map
- [math]\displaystyle{ U \mapsto \pi_U }[/math]
is a bijection between the set of strongly continuous unitary representations of G and non-degenerate bounded *-representations of Cc(G). This bijection respects unitary equivalence and strong containment. In particular, πU is irreducible if and only if U is irreducible.
Non-degeneracy of a representation π of Cc(G) on a Hilbert space Hπ means that
- [math]\displaystyle{ \left \{\pi(f) \xi : f \in \operatorname{C}_c(G), \xi \in H_\pi \right \} }[/math]
is dense in Hπ.
2.2. The Convolution Algebra L1(G)
It is a standard theorem of measure theory that the completion of Cc(G) in the L1(G) norm is isomorphic to the space L1(G) of equivalence classes of functions which are integrable with respect to the Haar measure, where, as usual, two functions are regarded as equivalent if and only if they differ only on a set of Haar measure zero.
Theorem. L1(G) is a Banach *-algebra with the convolution product and involution defined above and with the L1 norm. L1(G) also has a bounded approximate identity.
2.3. The Group C*-Algebra C*(G)
Let C[G] be the group ring of a discrete group G.
For a locally compact group G, the group C*-algebra C*(G) of G is defined to be the C*-enveloping algebra of L1(G), i.e. the completion of Cc(G) with respect to the largest C*-norm:
- [math]\displaystyle{ \|f\|_{C^*} := \sup_\pi \|\pi(f)\|, }[/math]
where π ranges over all non-degenerate *-representations of Cc(G) on Hilbert spaces. When G is discrete, it follows from the triangle inequality that, for any such π, one has:
- [math]\displaystyle{ \|\pi (f)\| \leq \| f \|_1, }[/math]
hence the norm is well-defined.
It follows from the definition that C*(G) has the following universal property: any *-homomorphism from C[G] to some B(H) (the C*-algebra of bounded operators on some Hilbert space H) factors through the inclusion map:
- [math]\displaystyle{ \mathbf{C}[G] \hookrightarrow C^*_{\max}(G). }[/math]
2.4. The Reduced Group C*-Algebra Cr*(G)
The reduced group C*-algebra Cr*(G) is the completion of Cc(G) with respect to the norm
- [math]\displaystyle{ \|f\|_{C^*_r} := \sup \left \{ \|f*g\|_2: \|g\|_2 = 1 \right \}, }[/math]
where
- [math]\displaystyle{ \|f\|_2 = \sqrt{\int_G |f|^2 \, d\mu} }[/math]
is the L2 norm. Since the completion of Cc(G) with regard to the L2 norm is a Hilbert space, the Cr* norm is the norm of the bounded operator acting on L2(G) by convolution with f and thus a C*-norm.
Equivalently, Cr*(G) is the C*-algebra generated by the image of the left regular representation on ℓ2(G).
In general, Cr*(G) is a quotient of C*(G). The reduced group C*-algebra is isomorphic to the non-reduced group C*-algebra defined above if and only if G is amenable.
2.5. von Neumann Algebras Associated to Groups
The group von Neumann algebra W*(G) of G is the enveloping von Neumann algebra of C*(G).
For a discrete group G, we can consider the Hilbert space ℓ2(G) for which G is an orthonormal basis. Since G operates on ℓ2(G) by permuting the basis vectors, we can identify the complex group ring C[G] with a subalgebra of the algebra of bounded operators on ℓ2(G). The weak closure of this subalgebra, NG, is a von Neumann algebra.
The center of NG can be described in terms of those elements of G whose conjugacy class is finite. In particular, if the identity element of G is the only group element with that property (that is, G has the infinite conjugacy class property), the center of NG consists only of complex multiples of the identity.
NG is isomorphic to the hyperfinite type II1 factor if and only if G is countable, amenable, and has the infinite conjugacy class property.
3. Stereotype Group Algebras
The full analogy with the purely algebraic situation appears in the stereotype theory where a series of natural group algebras is constructed including the following four examples.
- On each locally compact group [math]\displaystyle{ G }[/math] one can consider the algebra [math]\displaystyle{ {\mathcal C}(G) }[/math] of all continuous functions [math]\displaystyle{ u:G\to{\mathbb C} }[/math] with the pointwise multiplication. Being endowed with the topology of uniform convergence on compact sets [math]\displaystyle{ T\subseteq G }[/math], it becomes a stereotype algebra. Its stereotype dual space [math]\displaystyle{ {\mathcal C}^\star(G) }[/math], which consists of Radon measures with compact support on [math]\displaystyle{ G }[/math], is a stereotype algebra with respect to the operation of convolution:[3] [math]\displaystyle{ \alpha * \beta (u)= \int_G \left( \int_G u(s\cdot t)\, \alpha(ds) \right) \beta(dt), \quad \alpha,\beta\in {\mathcal C}^\star(G), \ u\in {\mathcal C}(G). }[/math]
- The algebra [math]\displaystyle{ {\mathcal C}^\star(G) }[/math] is called the stereotype group algebra of measures on the locally compact group [math]\displaystyle{ G }[/math].[4]
- On each real Lie group [math]\displaystyle{ G }[/math] one can consider the algebra [math]\displaystyle{ {\mathcal E}(G) }[/math] of all smooth functions [math]\displaystyle{ u:G\to{\mathbb C} }[/math] with the pointwise multiplication, and the topology of uniform convergence with all derivatives on compact sets [math]\displaystyle{ T\subseteq G }[/math]. Again, it is a stereotype algebra. Its stereotype dual space [math]\displaystyle{ {\mathcal E}^\star(G) }[/math], which consists of distributions with compact support on [math]\displaystyle{ G }[/math], is a stereotype algebra with respect to the operation of convolution of distributions. The algebra [math]\displaystyle{ {\mathcal E}^\star(G) }[/math] is called the stereotype group algebra of distributions on the real Lie group [math]\displaystyle{ G }[/math].
- On each Stein group[5] [math]\displaystyle{ G }[/math] one can consider the algebra [math]\displaystyle{ {\mathcal O}(G) }[/math] of all holomorphic functions [math]\displaystyle{ u:G\to{\mathbb C} }[/math] with the pointwise multiplication and the topology of uniform convergence on compact sets [math]\displaystyle{ T\subseteq G }[/math]. Again, this is a stereotype algebra. Its stereotype dual space [math]\displaystyle{ {\mathcal O}^\star(G) }[/math], which consists of holomorphic fuhctionals on [math]\displaystyle{ G }[/math], is a stereotype algebra with respect to the operation of convolution of functionals. The algebra [math]\displaystyle{ {\mathcal O}^\star(G) }[/math] is called the stereotype group algebra of analytic functionals on the Stein group [math]\displaystyle{ G }[/math].
- On each affine algebraic group [math]\displaystyle{ G }[/math] one can consider the algebra [math]\displaystyle{ {\mathcal P}(G) }[/math] of all polynomials (or regular functions) [math]\displaystyle{ u:G\to{\mathbb C} }[/math] with the pointwise multiplication and the strongest locally convex topology. This is again a stereotype algebra, and its stereotype dual space [math]\displaystyle{ {\mathcal P}^\star(G) }[/math], which consists of currents on [math]\displaystyle{ G }[/math], is a stereotype algebra with respect to the operation of convolution of currents. The algebra [math]\displaystyle{ {\mathcal P}^\star(G) }[/math] is called the stereotype group algebra of currents on the affine algebraic group [math]\displaystyle{ G }[/math].
The representation[6] [math]\displaystyle{ \delta: G\to {\mathcal C}^\star(G) }[/math], [math]\displaystyle{ \delta(x)(u)=u(x) }[/math], [math]\displaystyle{ x\in G }[/math], [math]\displaystyle{ u\in {\mathcal C}^\star(G) }[/math] is called the representation as delta-functionals.
The representations [math]\displaystyle{ \delta: G\to {\mathcal E}^\star(G) }[/math], [math]\displaystyle{ \delta: G\to {\mathcal O}^\star(G) }[/math], [math]\displaystyle{ \delta: G\to {\mathcal P}^\star(G) }[/math], are defined similarly.
The following two results distinguish the stereotype group algebras among the other models of group algebras in analysis.
- Theorem (universal property).[7]
For any stereotype algebra [math]\displaystyle{ A }[/math] the formula
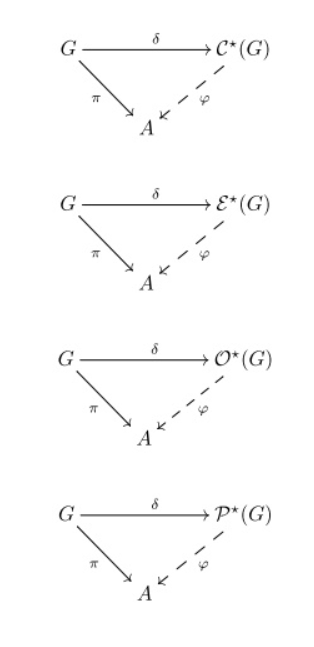 Universal property of stereotype group algebras. https://handwiki.org/wiki/index.php?curid=1471305
Universal property of stereotype group algebras. https://handwiki.org/wiki/index.php?curid=1471305
- [math]\displaystyle{ \pi=\varphi\circ\delta }[/math]
- establishes a one-to-one correspondence between
-
- the continuous representations[6] [math]\displaystyle{ \pi:G\to A }[/math] of any given locally compact group [math]\displaystyle{ G }[/math] in the stereotype algebra [math]\displaystyle{ A }[/math] and the morphisms of stereotype algebras [math]\displaystyle{ \varphi:{\mathcal C}^\star(G)\to A }[/math],
-
- the holomorphic[9] representations[6] [math]\displaystyle{ \pi:G\to A }[/math] of any given Stein group [math]\displaystyle{ G }[/math] in the stereotype algebra [math]\displaystyle{ A }[/math] and the morphisms of stereotype algebras [math]\displaystyle{ \varphi:{\mathcal O}^\star(G)\to A }[/math],
-
- the polynomial (regular)[10] representations[6] [math]\displaystyle{ \pi:G\to A }[/math] of any given affine algebraic group [math]\displaystyle{ G }[/math] in the stereotype algebra [math]\displaystyle{ A }[/math] and the morphisms of stereotype algebras [math]\displaystyle{ \varphi:{\mathcal P}^\star(G)\to A }[/math].
- Theorem.[11] The group algebras [math]\displaystyle{ {\mathcal C}^\star(G) }[/math], [math]\displaystyle{ {\mathcal E}^\star(G) }[/math], [math]\displaystyle{ {\mathcal O}^\star(G) }[/math], [math]\displaystyle{ {\mathcal P}^\star(G) }[/math] are Hopf algebras in the monoidal category (Ste,[math]\displaystyle{ \circledast }[/math],[math]\displaystyle{ {\mathbb C} }[/math]) of stereotype spaces.
References
- Lang 2002, Chapter XVIII.
- Vinberg 2003, 12.4.
- Akbarov 2003, p. 272.
- If [math]\displaystyle{ G }[/math] is an infinite locally compact group then the algebra [math]\displaystyle{ {\mathcal C}^\star(G) }[/math] of measures on [math]\displaystyle{ G }[/math] is not a Fréchet algebra. In the case when [math]\displaystyle{ G }[/math] is compact, [math]\displaystyle{ {\mathcal C}^\star(G) }[/math] is a Smith space. If [math]\displaystyle{ G }[/math] is [math]\displaystyle{ \sigma }[/math]-compact, then [math]\displaystyle{ {\mathcal C}^\star(G) }[/math] is a Brauner space.
- A Stein group is a complex Lie group [math]\displaystyle{ G }[/math] which is a Stein manifold.
- We use here the definition given above: a map [math]\displaystyle{ \pi:G\to A }[/math] of a group [math]\displaystyle{ G }[/math] into a unital associative algebra [math]\displaystyle{ A }[/math] over [math]\displaystyle{ K }[/math] is called a representation of the group [math]\displaystyle{ G }[/math] in the algebra [math]\displaystyle{ A }[/math], if it preserves the unit and the multiplication: [math]\displaystyle{ \pi(1_G)=1_A,\quad \pi(s\cdot t)=\pi(s)\cdot\pi(t),\quad s,t\in G. }[/math]
- Akbarov 2003, p. 275.
- A map [math]\displaystyle{ \xi:M\to X }[/math] of a smooth manifold [math]\displaystyle{ M }[/math] into a stereotype space [math]\displaystyle{ X }[/math] is said to be smooth if for each functional [math]\displaystyle{ f\in X^\star }[/math] the composition [math]\displaystyle{ f\circ\xi }[/math] is a smooth function on [math]\displaystyle{ M }[/math], and the map [math]\displaystyle{ f\in X^\star\mapsto f\circ\xi\in {\mathcal E}(M) }[/math] is continuous.
- A map [math]\displaystyle{ \xi:M\to X }[/math] of a Stein manifold [math]\displaystyle{ M }[/math] into a stereotype space [math]\displaystyle{ X }[/math] is said to be holomorphic if for each functional [math]\displaystyle{ f\in X^\star }[/math] the composition [math]\displaystyle{ f\circ\xi }[/math] is a holomorphic function on [math]\displaystyle{ M }[/math], and the map [math]\displaystyle{ f\in X^\star\mapsto f\circ\xi\in {\mathcal O}(M) }[/math] is continuous.
- A map [math]\displaystyle{ \xi:M\to X }[/math] of an affine algebraic variety [math]\displaystyle{ M }[/math] over [math]\displaystyle{ {\mathbb C} }[/math] into a stereotype space [math]\displaystyle{ X }[/math] is said to be polynomial (or regular) if for each functional [math]\displaystyle{ f\in X^\star }[/math] the composition [math]\displaystyle{ f\circ\xi }[/math] is a polynomial on [math]\displaystyle{ M }[/math], and the map [math]\displaystyle{ f\in X^\star\mapsto f\circ\xi\in {\mathcal P}(M) }[/math] is continuous.
- Akbarov 2009, p. 507.




