1. Applications

Fuzzy logic can be used to control household appliances such as washing machines (which sense load size and detergent concentration and adjust their wash cycles accordingly) and refrigerators.

A basic application might characterize subranges of a continuous variable. For instance, a temperature measurement for anti-lock brakes might have several separate membership functions defining particular temperature ranges needed to control the brakes properly. Each function maps the same temperature value to a truth value in the 0 to 1 range. These truth values can then be used to determine how the brakes should be controlled.

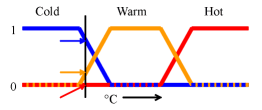
In this image, cold, warm, and hot are functions mapping a temperature scale. A point on that scale has three "truth values" — one for each of the three functions. For the particular temperature shown, the three truth values could be interpreted as describing the temperature as, say, "fairly cold", "slightly warm", and "not hot".

2. Misconceptions and Controversies

Fuzzy logic is the same as "imprecise logic".

Fuzzy logic is not any less precise than any other form of logic: it is an organized and mathematical method of handling inherently imprecise concepts. The concept of "coldness" cannot be expressed in an equation, because although temperature is a quantity, "coldness" is not. However, people have an idea of what "cold" is, and agree that there is no sharp cutoff between "cold" and "not cold", where something is "cold" at N degrees but "not cold" at N+1 degrees — a concept classical logic cannot easily handle due to the principle of bivalence.

Fuzzy logic is a new way of expressing probability.

Fuzzy logic and probability refer to different kinds of uncertainty. Fuzzy logic is specifically designed to deal with imprecision of facts (fuzzy logic statements), while probability deals with chances of that happening (but still considering the result to be precise). However, this is a point of controversy. Many statisticians are persuaded by the work of Bruno de Finetti that only one kind of mathematical uncertainty is needed and thus fuzzy logic is unnecessary. On the other hand, Bart Kosko argues that probability is a subtheory of fuzzy logic, as probability only handles one kind of uncertainty. He also claims to have proven a derivation of Bayes' theorem from the concept of fuzzy subsethood. Lotfi Zadeh, the creator of fuzzy logic, argues that fuzzy logic is different in character from probability, and is not a replacement for it. He has created a fuzzy alternative to probability, which he calls possibility theory. Other controversial approaches to uncertainty include Dempster-Shafer theory and rough sets.

Fuzzy logic will be difficult to scale to larger problems.

In a widely circulated and highly controversial paper, Charles Elkan in 1993 commented that "...there are few, if any, published reports of expert systems in real-world use that reason about uncertainty using fuzzy logic. It appears that the limitations of fuzzy logic have not been detrimental in control applications because current fuzzy controllers are far simpler than other knowledge-based systems. In future, the technical limitations of fuzzy logic can be expected to become important in practice, and work on fuzzy controllers will also encounter several problems of scale already known for other knowledge-based systems". Reactions to Elkan's paper are many and varied, from claims that he is simply mistaken, to others who accept that he has identified important limitations of fuzzy logic that need to be addressed by system designers. In fact, fuzzy logic wasn't largely used at that time, and today it is used to solve very complex problems in the AI area.

3. Examples Where Fuzzy Logic Is Used

• Automobile and other vehicle subsystems, such as ABS and cruise control (e.g. Tokyo monorail)
• Air conditioners
• The MASSIVE engine used in the Lord of the Rings films, which helped show huge scale armies create random, yet orderly movements
• Cameras
• Digital image processing, such as edge detection
• Rice cookers
• Dishwashers
• Elevators
• Carbon dioxide enrichment burner's controllers
• Washing machines and other home appliances
• Video game artificial intelligence
• Language filters on message boards and chat rooms for filtering out offensive text
• Pattern recognition in Remote Sensing
• Fuzzy logic has also been incorporated into some microcontrollers and microprocessors, for instance, the Freescale 68HC12.

4. How Fuzzy Logic Is Applied

Fuzzy Set Theory defines Fuzzy Operators on Fuzzy Sets. The problem in applying this is that the appropriate Fuzzy Operator may not be known! For this reason, Fuzzy logic usually uses IF/THEN rules, or constructs that are equivalent, such as fuzzy associative matrices.

Rules are usually expressed in the form:
IF variable IS set THEN action

For example, an extremely simple temperature regulator that uses a fan might look like this:
IF temperature IS very cold THEN stop fan
IF temperature IS cold THEN turn down fan
IF temperature IS normal THEN maintain level
IF temperature IS hot THEN speed up fan

Notice there is no "ELSE". All of the rules are evaluated, because the temperature might be "cold" and "normal" at the same time to differing degrees.

The AND, OR, and NOT operators of boolean logic exist in fuzzy logic, usually defined as the minimum, maximum, and complement; when they are defined this way, they are called the Zadeh operators, because they were first defined as such in Zadeh's original papers. So for the fuzzy variables x and y:

NOT x = (1 - truth(x))

x AND y = minimum(truth(x), truth(y))

x OR y = maximum(truth(x), truth(y))

There are also other operators, more linguistic in nature, called hedges that can be applied. These are generally adverbs such as "very", or "somewhat", which modify the meaning of a set using a mathematical formula.

In application, the programming language Prolog is well geared to implementing fuzzy logic with its facilities to set up a database of "rules" which are queried to deduct logic. This sort of programming is known as logic programming.

Once fuzzy relations are defined, it is possible to develop fuzzy relational databases. The first fuzzy relational data base, FRDB, appeared in Maria Zemankova's dissertation.

4.1. Other Examples

• If a man is 1.8 meters, consider him as tall:

IF male IS true AND height >= 1.8 THEN is_tall IS true; is_short IS false

• The fuzzy rules do not make the sharp distinction between tall and short, that is not so realistic:

IF height <= medium male THEN is_short IS agree somewhat
IF height >= medium male THEN is_tall IS agree somewhat

In the fuzzy case, there are no such heights like 1.83 meters, but there are fuzzy values, like the following assignments:

dwarf male = [0, 1.3] m
short male = (1.3, 1.5]
medium male = (1.5, 1.8]
tall male = (1.8, 2.0]
giant male > 2.0 m

For the consequent, there are also not only two values, but five, say:

agree not = 0
agree little = 1
agree somewhat = 2
agree a lot = 3
agree fully = 4

In the binary, or "crisp", case, a person of 1.79 meters of height is considered short. If another person is 1.8 meters or 2.25 meters, these persons are considered tall.

The crisp example differs deliberately from the fuzzy one. We did not put in the antecedent

IF male >= agree somewhat AND ...

as gender is often considered as a binary information. So, it is not so complex as being tall.

5. Formal Fuzzy Logic

In mathematical logic, there are several formal systems that model the above notions of "fuzzy logic". Note that they use a different set of operations than above mentioned Zadeh operators.

5.1. Propositional Fuzzy Logics

• Basic propositional fuzzy logic BL is an axiomatization of logic where conjunction is defined by a continuous t-norm, and implication is defined as the residuum of the t-norm. Its models correspond to BL-algebras.
• Łukasiewicz fuzzy logic is a special case of basic fuzzy logic where conjunction is Łukasiewicz t-norm. It has the axioms of basic logic plus an axiom of double negation (so it is not intuitionistic logic), and its models correspond to MV-algebras.
• Gödel fuzzy logic is a special case of basic fuzzy logic where conjunction is Gödel t-norm. It has the axioms of basic logic plus an axiom of idempotence of conjunction, and its models are called G-algebras.
• Product fuzzy logic is a special case of basic fuzzy logic where conjunction is product t-norm. It has the axioms of basic logic plus another axiom, and its models are called product algebras.
• Monoidal t-norm logic MTL is a generalization of basic fuzzy logic BL where conjunction is realized by a left-continuous t-norm. Its models (MTL-algebras) are prelinear commutative bounded integral residuated lattices.
• Rational Pavelka logic is a generalization of multi-valued logic. It is an extension of Łukasziewicz fuzzy logic with additional constants.

All these logics encompass the traditional propositional logic (whose models correspond to Boolean algebras).

5.2. Predicate Fuzzy Logics

These extend the above-mentioned fuzzy logics by adding universal and existential quantifiers in a manner similar to the way that predicate logic is created from propositional logic.

5.3. Effectiveness for Fuzzy Logics

The notions of a "decidable subset" and "recursively enumerable subset" are basic ones for classical mathematics and classical logic. Then, the question of a suitable extension of such concepts to fuzzy set theory arises. A first proposal in such a direction was made by E.S. Santos by the notions of fuzzy Turing machine, Markov normal fuzzy algorithm and fuzzy program. Successively, L. Biacino and G. Gerla proposed the following definition where Ü denotes the set of rational numbers in [0,1]. A fuzzy subset μ : S [math]\displaystyle{ \rightarrow }[/math][0,1] of a set S is recursively enumerable if a recursive map h : S×N [math]\displaystyle{ \rightarrow }[/math]Ü exists such that, for every x in S, the function h(x,n) is increasing with respect to n and μ(x) = lim h(x,n). We say that μ is decidable if both μ and its complement –μ are recursively enumerable. An extension of such a theory to the general case of the L-subsets is proposed in a paper by G. Gerla. The proposed definitions are well related with fuzzy logic. Indeed, the following theorem holds true (provided that the deduction apparatus of the fuzzy logic satisfies some obvious effectiveness property).

Theorem. Any axiomatizable fuzzy theory is recursively enumerable. In particular, the fuzzy set of logically true formulas is recursively enumerable in spite of the fact that the crisp set of valid formulas is not recursively enumerable, in general. Moreover, any axiomatizable and complete theory is decidable.

It is an open question to give a support for a Church thesis for fuzzy computability and to give Gödel’s theorems for fuzzy logic using the notion of recursively enumerable fuzzy subset. To this aim, it is very important to refer to adequate definitions of fuzzy grammar and of fuzzy Turing machine (see for example Wiedermann's paper).