
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Camila Xu | -- | 2551 | 2022-11-02 01:49:44 |
Video Upload Options
In Euclidean geometry, a bicentric quadrilateral is a convex quadrilateral that has both an incircle and a circumcircle. The radii and center of these circles are called inradius and circumradius, and incenter and circumcenter respectively. From the definition it follows that bicentric quadrilaterals have all the properties of both tangential quadrilaterals and cyclic quadrilaterals. Other names for these quadrilaterals are chord-tangent quadrilateral and inscribed and circumscribed quadrilateral. It has also rarely been called a double circle quadrilateral and double scribed quadrilateral. If two circles, one within the other, are the incircle and the circumcircle of a bicentric quadrilateral, then every point on the circumcircle is the vertex of a bicentric quadrilateral having the same incircle and circumcircle. This is a corollary of Poncelet's porism, which was proved by the French mathematician Jean-Victor Poncelet (1788–1867).
1. Special Cases
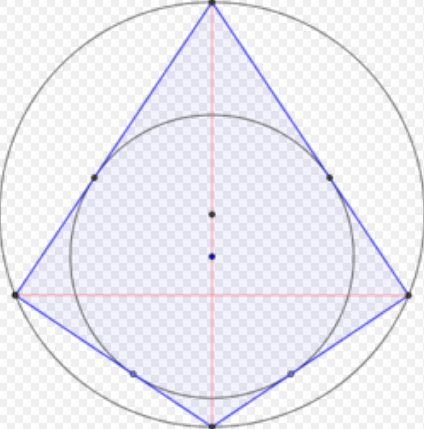
Examples of bicentric quadrilaterals are squares, right kites, and isosceles tangential trapezoids.
2. Characterizations

A convex quadrilateral ABCD with sides a, b, c, d is bicentric if and only if opposite sides satisfy Pitot's theorem for tangential quadrilaterals and the cyclic quadrilateral property that opposite angles are supplementary; that is,
- [math]\displaystyle{ \begin{cases} a+c=b+d\\ A+C=B+D=\pi. \end{cases} }[/math]
Three other characterizations concern the points where the incircle in a tangential quadrilateral is tangent to the sides. If the incircle is tangent to the sides AB, BC, CD, DA at W, X, Y, Z respectively, then a tangential quadrilateral ABCD is also cyclic if and only if any one of the following three conditions holds:[1]
- WY is perpendicular to XZ
- [math]\displaystyle{ \frac{AW}{WB}=\frac{DY}{YC} }[/math]
- [math]\displaystyle{ \frac{AC}{BD}=\frac{AW+CY}{BX+DZ} }[/math]
The first of these three means that the contact quadrilateral WXYZ is an orthodiagonal quadrilateral.
If E, F, G, H are the midpoints of WX, XY, YZ, ZW respectively, then the tangential quadrilateral ABCD is also cyclic if and only if the quadrilateral EFGH is a rectangle.[1]
According to another characterization, if I is the incenter in a tangential quadrilateral where the extensions of opposite sides intersect at J and K, then the quadrilateral is also cyclic if and only if JIK is a right angle.[1]
Yet another necessary and sufficient condition is that a tangential quadrilateral ABCD is cyclic if and only if its Newton line is perpendicular to the Newton line of its contact quadrilateral WXYZ. (The Newton line of a quadrilateral is the line defined by the midpoints of its diagonals.)[1]
3. Construction
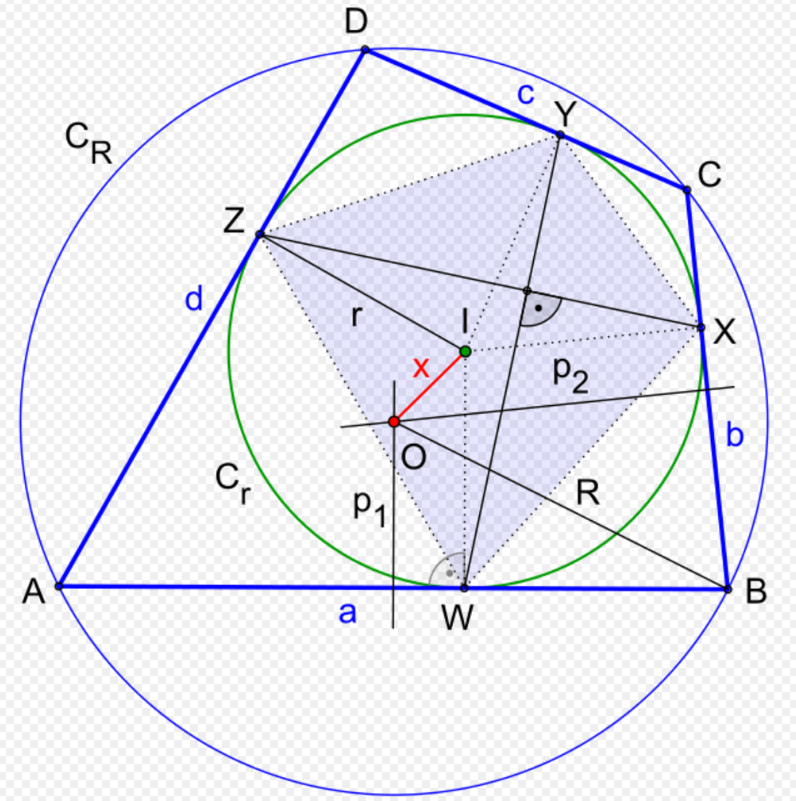
There is a simple method for constructing a bicentric quadrilateral:
It starts with the incircle Cr around the centre I with the radius r and then draw two to each other perpendicular chords WY and XZ in the incircle Cr. At the endpoints of the chords draw the tangents a, b, c and d to the incircle. These intersect at four points A, B, C and D, which are the vertices of a bicentric quadrilateral.[2] To draw the circumcircle, draw two perpendicular bisectors p1 and p2 on the sides of the bicentric quadrilateral a respectively b. The perpendicular bisectors p1 and p2 intersect in the centre O of the circumcircle CR with the distance x to the centre I of the incircle Cr. The circumcircle can be drawn around the centre O.
The validity of this construction is due to the characterization that, in a tangential quadrilateral ABCD, the contact quadrilateral WXYZ has perpendicular diagonals if and only if the tangential quadrilateral is also cyclic.
4. Area
4.1. Formulas in Terms of Four Quantities
The area K of a bicentric quadrilateral can be expressed in terms of four quantities of the quadrilateral in several different ways. If the sides are a, b, c, d, then the area is given by[3][4][5][6][7]
- [math]\displaystyle{ \displaystyle K = \sqrt{abcd}. }[/math]
This is a special case of Brahmagupta's formula. It can also be derived directly from the trigonometric formula for the area of a tangential quadrilateral. Note that the converse does not hold: Some quadrilaterals that are not bicentric also have area [math]\displaystyle{ \displaystyle K = \sqrt{abcd}. }[/math][8] One example of such a quadrilateral is a non-square rectangle.
The area can also be expressed in terms of the tangent lengths e, f, g, h as[4]:p.128
- [math]\displaystyle{ K=\sqrt[4]{efgh}(e+f+g+h). }[/math]
A formula for the area of bicentric quadrilateral ABCD with incenter I is[5]
- [math]\displaystyle{ K=AI\cdot CI+BI\cdot DI. }[/math]
If a bicentric quadrilateral has tangency chords k, l and diagonals p, q, then it has area[4]:p.129
- [math]\displaystyle{ K=\frac{klpq}{k^2+l^2}. }[/math]
If k, l are the tangency chords and m, n are the bimedians of the quadrilateral, then the area can be calculated using the formula[5]
- [math]\displaystyle{ K=\left|\frac{m^2-n^2}{k^2-l^2}\right|kl }[/math]
This formula cannot be used if the quadrilateral is a right kite, since the denominator is zero in that case.
If M and N are the midpoints of the diagonals, and E and F are the intersection points of the extensions of opposite sides, then the area of a bicentric quadrilateral is given by
- [math]\displaystyle{ K=\frac{2MN\cdot EI\cdot FI}{EF} }[/math]
where I is the center of the incircle.[5]
4.2. Formulas in Terms of Three Quantities
The area of a bicentric quadrilateral can be expressed in terms of two opposite sides and the angle θ between the diagonals according to[5]
- [math]\displaystyle{ K=ac\tan{\frac{\theta}{2}}=bd\cot{\frac{\theta}{2}}. }[/math]
In terms of two adjacent angles and the radius r of the incircle, the area is given by[5]
- [math]\displaystyle{ K=2r^2\left(\frac{1}{\sin{A}}+\frac{1}{\sin{B}}\right). }[/math]
The area is given in terms of the circumradius R and the inradius r as
- [math]\displaystyle{ K=r(r+\sqrt{4R^2+r^2})\sin \theta }[/math]
where θ is either angle between the diagonals.[9]
If M and N are the midpoints of the diagonals, and E and F are the intersection points of the extensions of opposite sides, then the area can also be expressed as
- [math]\displaystyle{ K=2MN\sqrt{EQ\cdot FQ} }[/math]
where Q is the foot of the perpendicular to the line EF through the center of the incircle.[5]
4.3. Inequalities
If r and R are the inradius and the circumradius respectively, then the area K satisfies the inequalities[10]
- [math]\displaystyle{ \displaystyle 4r^2 \le K \le 2R^2. }[/math]
There is equality on either side only if the quadrilateral is a square.
Another inequality for the area is[11]:p.39,#1203
- [math]\displaystyle{ K \le \tfrac{4}{3}r\sqrt{4R^2+r^2} }[/math]
where r and R are the inradius and the circumradius respectively.
A similar inequality giving a sharper upper bound for the area than the previous one is[9]
- [math]\displaystyle{ K \le r(r+\sqrt{4R^2+r^2}) }[/math]
with equality holding if and only if the quadrilateral is a right kite.
In addition, with sides a, b, c, d and semiperimeter s:
- [math]\displaystyle{ 2\sqrt{K} \leq s \leq r+ \sqrt{r^2+4R^2}; }[/math][11]:p.39,#1203
- [math]\displaystyle{ 6K \leq ab+ac+ad+bc+bd+cd \leq 4r^2+4R^2+ 4r\sqrt{r^2+4R^2}; }[/math][11]:p.39,#1203
- [math]\displaystyle{ 4Kr^2\leq abcd \leq \frac{16}{9} r^2(r^2+4R^2). }[/math][11]:p.39,#1203
5. Angle Formulas
If a, b, c, d are the length of the sides AB, BC, CD, DA respectively in a bicentric quadrilateral ABCD, then its vertex angles can be calculated with the tangent function:[5]
- [math]\displaystyle{ \tan{\frac{A}{2}}=\sqrt{\frac{bc}{ad}}=\cot{\frac{C}{2}}, }[/math]
- [math]\displaystyle{ \tan{\frac{B}{2}}=\sqrt{\frac{cd}{ab}}=\cot{\frac{D}{2}}. }[/math]
Using the same notations, for the sine and cosine functions the following formulas holds:[12]
- [math]\displaystyle{ \sin{\frac{A}{2}}=\sqrt{\frac{bc}{ad+bc}}=\cos{\frac{C}{2}}, }[/math]
- [math]\displaystyle{ \cos{\frac{A}{2}}=\sqrt{\frac{ad}{ad+bc}}=\sin{\frac{C}{2}}, }[/math]
- [math]\displaystyle{ \sin{\frac{B}{2}}=\sqrt{\frac{cd}{ab+cd}}=\cos{\frac{D}{2}}, }[/math]
- [math]\displaystyle{ \cos{\frac{B}{2}}=\sqrt{\frac{ab}{ab+cd}}=\sin{\frac{D}{2}}. }[/math]
The angle θ between the diagonals can be calculated from[6]
- [math]\displaystyle{ \displaystyle \tan{\frac{\theta}{2}}=\sqrt{\frac{bd}{ac}}. }[/math]
6. Inradius and Circumradius
The inradius r of a bicentric quadrilateral is determined by the sides a, b, c, d according to[3]
- [math]\displaystyle{ \displaystyle r=\frac{\sqrt{abcd}}{a+c}=\frac{\sqrt{abcd}}{b+d}. }[/math]
The circumradius R is given as a special case of Parameshvara's formula. It is[3]
- [math]\displaystyle{ \displaystyle R=\frac{1}{4}\sqrt{\frac{(ab+cd)(ac+bd)(ad+bc)}{abcd}}. }[/math]
The inradius can also be expressed in terms of the consecutive tangent lengths e, f, g, h according to[13]:p. 41
- [math]\displaystyle{ \displaystyle r=\sqrt{eg}=\sqrt{fh}. }[/math]
These two formulas are in fact necessary and sufficient conditions for a tangential quadrilateral with inradius r to be cyclic.
The four sides a, b, c, d of a bicentric quadrilateral are the four solutions of the quartic equation
- [math]\displaystyle{ y^4-2sy^3+(s^2+2r^2+2r\sqrt{4R^2+r^2})y^2-2rs(\sqrt{4R^2+r^2}+r)y+r^2s^2=0 }[/math]
where s is the semiperimeter, and r and R are the inradius and circumradius respectively.[14]:p. 754
If there is a bicentric quadrilateral with inradius r whose tangent lengths are e, f, g, h, then there exists a bicentric quadrilateral with inradius rv whose tangent lengths are ev, fv, gv, hv, where v may be any real number.[15]:pp.9–10
A bicentric quadrilateral has a greater inradius than does any other tangential quadrilateral having the same sequence of side lengths.[16]:pp.392–393
6.1. Inequalities
The circumradius R and the inradius r satisfy the inequality
- [math]\displaystyle{ R\ge \sqrt{2}r }[/math]
which was proved by L. Fejes Tóth in 1948.[15] It holds with equality only when the two circles are concentric (have the same center as each other); then the quadrilateral is a square. The inequality can be proved in several different ways, one using the double inequality for the area above.
An extension of the previous inequality is[17][18]:p. 141
- [math]\displaystyle{ \frac{r\sqrt{2}}{R}\le \frac{1}{2}\left(\sin{\frac{A}{2}}\cos{\frac{B}{2}}+\sin{\frac{B}{2}}\cos{\frac{C}{2}}+\sin{\frac{C}{2}}\cos{\frac{D}{2}}+\sin{\frac{D}{2}}\cos{\frac{A}{2}}\right)\le 1 }[/math]
where there is equality on either side if and only if the quadrilateral is a square.[12]:p. 81
The semiperimeter s of a bicentric quadrilateral satisfies[15]:p.13
- [math]\displaystyle{ \sqrt{8r\left(\sqrt{4R^2+r^2}-r\right)}\le s \le \sqrt{4R^2+r^2}+r }[/math]
where r and R are the inradius and circumradius respectively.
Moreover,[11]:p.39,#1203
- [math]\displaystyle{ 2sr^2\leq abc+abd+acd+bcd \leq 2r(r+\sqrt{r^2+4R^2})^2 }[/math]
and
- [math]\displaystyle{ abc+abd+acd+bcd \leq 2\sqrt{K}(K+2R^2). }[/math] [11]:p.62,#1599
7. Distance Between the Incenter and Circumcenter
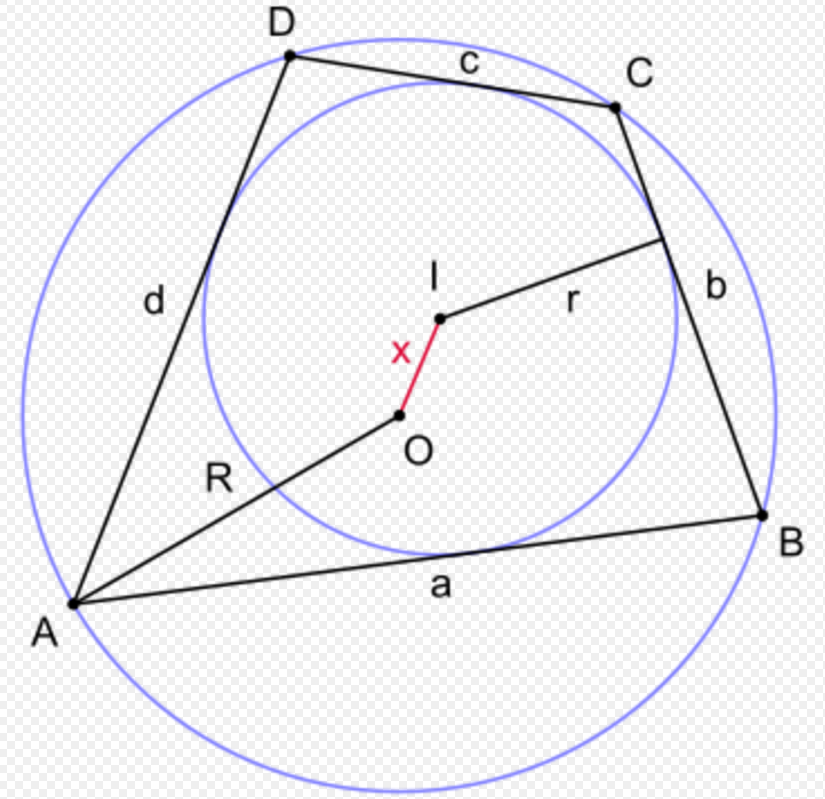
7.1. Fuss' Theorem
Fuss' theorem gives a relation between the inradius r, the circumradius R and the distance x between the incenter I and the circumcenter O, for any bicentric quadrilateral. The relation is[7][19][20]
- [math]\displaystyle{ \frac{1}{(R-x)^2}+\frac{1}{(R+x)^2}=\frac{1}{r^2}, }[/math]
or equivalently
- [math]\displaystyle{ \displaystyle 2r^2(R^2+x^2)=(R^2-x^2)^2. }[/math]
It was derived by Nicolaus Fuss (1755–1826) in 1792. Solving for x yields
- [math]\displaystyle{ x=\sqrt{R^2+r^2-r\sqrt{4R^2+r^2}}. }[/math]
Fuss's theorem, which is the analog of Euler's theorem for triangles for bicentric quadrilaterals, says that if a quadrilateral is bicentric, then its two associated circles are related according to the above equations. In fact the converse also holds: given two circles (one within the other) with radii R and r and distance x between their centers satisfying the condition in Fuss' theorem, there exists a convex quadrilateral inscribed in one of them and tangent to the other[21] (and then by Poncelet's closure theorem, there exist infinitely many of them).
Applying [math]\displaystyle{ x^2 \ge 0 }[/math] to the expression of Fuss's theorem for x in terms of r and R is another way to obtain the above-mentioned inequality [math]\displaystyle{ R \ge \sqrt{2}r. }[/math] A generalization is[15]:p.5
- [math]\displaystyle{ 2r^2+x^2\le R^2 \le 2r^2+x^2+2rx. }[/math]
7.2. Carlitz' Identity
Another formula for the distance x between the centers of the incircle and the circumcircle is due to the American mathematician Leonard Carlitz (1907–1999). It states that[22]
- [math]\displaystyle{ \displaystyle x^2=R^2-2Rr\cdot \mu }[/math]
where r and R are the inradius and the circumradius respectively, and
- [math]\displaystyle{ \displaystyle \mu=\sqrt{\frac{(ab+cd)(ad+bc)}{(a+c)^2(ac+bd)}} = \sqrt{\frac{(ab+cd)(ad+bc)}{(b+d)^2(ac+bd)}} }[/math]
where a, b, c, d are the sides of the bicentric quadrilateral.
7.3. Inequalities for the Tangent Lengths and Sides
For the tangent lengths e, f, g, h the following inequalities holds:[15]:p.3
- [math]\displaystyle{ 4r\le e+f+g+h \le 4r\cdot \frac{R^2+x^2}{R^2-x^2} }[/math]
and
- [math]\displaystyle{ 4r^2\le e^2+f^2+g^2+h^2 \le 4(R^2+x^2-r^2) }[/math]
where r is the inradius, R is the circumradius, and x is the distance between the incenter and circumcenter. The sides a, b, c, d satisfy the inequalities[15]:p.5
- [math]\displaystyle{ 8r\le a+b+c+d \le 8r\cdot \frac{R^2+x^2}{R^2-x^2} }[/math]
and
- [math]\displaystyle{ 4(R^2-x^2+2r^2)\le a^2+b^2+c^2+d^2 \le 4(3R^2-2r^2). }[/math]
8. Other Properties of the Incenter
The circumcenter, the incenter, and the intersection of the diagonals in a bicentric quadrilateral are collinear.[23]
There is the following equality relating the four distances between the incenter I and the vertices of a bicentric quadrilateral ABCD:[24]
- [math]\displaystyle{ \frac{1}{AI^2}+\frac{1}{CI^2}=\frac{1}{BI^2}+\frac{1}{DI^2}=\frac{1}{r^2} }[/math]
where r is the inradius.
If P is the intersection of the diagonals in a bicentric quadrilateral ABCD with incenter I, then[25]
- [math]\displaystyle{ \frac{AP}{CP}=\frac{AI^2}{CI^2}. }[/math]
An inequality concerning the inradius r and circumradius R in a bicentric quadrilateral ABCD is[26]
- [math]\displaystyle{ 4r^2 \le AI\cdot CI+BI\cdot DI \le 2R^2 }[/math]
where I is the incenter.
9. Properties of the Diagonals
The lengths of the diagonals in a bicentric quadrilateral can be expressed in terms of the sides or the tangent lengths, which are formulas that holds in a cyclic quadrilateral and a tangential quadrilateral respectively.
In a bicentric quadrilateral with diagonals p and q, the following identity holds:[7]
- [math]\displaystyle{ \displaystyle \frac{pq}{4r^2}-\frac{4R^2}{pq}=1 }[/math]
where r and R are the inradius and the circumradius respectively. This equality can be rewritten as[9]
- [math]\displaystyle{ r=\frac{pq}{2\sqrt{pq+4R^2}} }[/math]
or, solving it as a quadratic equation for the product of the diagonals, in the form
- [math]\displaystyle{ pq=2r\left(r+\sqrt{4R^2+r^2}\right). }[/math]
An inequality for the product of the diagonals p, q in a bicentric quadrilateral is[10]
- [math]\displaystyle{ \displaystyle 8pq\le (a+b+c+d)^2 }[/math]
where a, b, c, d are the sides. This was proved by Murray S. Klamkin in 1967.
10. Four Incenters Lie on a Circle
Let ABCD be a bicentric quadrilateral, O is center of circle (ABCD). Then Incenters of four triangles OAB, OBC, OCD, ODA lie on a circle.[27]
References
- Josefsson, Martin (2010), "Characterizations of Bicentric Quadrilaterals", Forum Geometricorum 10: 165–173, http://forumgeom.fau.edu/FG2010volume10/FG201019.pdf .
- Alsina, Claudi; Nelsen, Roger (2011). Icons of Mathematics. An exploration of twenty key images. Mathematical Association of America. pp. 125–126. ISBN 978-0-88385-352-8.
- Weisstein, Eric, Bicentric Quadrilateral at MathWorld, [3], Accessed on 2011-08-13.
- Josefsson, Martin (2010), "Calculations concerning the tangent lengths and tangency chords of a tangential quadrilateral", Forum Geometricorum 10: 119–130, http://forumgeom.fau.edu/FG2010volume10/FG201013.pdf .
- Josefsson, Martin (2011), "The Area of a Bicentric Quadrilateral", Forum Geometricorum 11: 155–164, http://forumgeom.fau.edu/FG2011volume11/FG201116.pdf .
- Durell, C. V. and Robson, A., Advanced Trigonometry, Dover, 2003, pp. 28, 30.
- Yiu, Paul, Euclidean Geometry, [4], 1998, pp. 158-164.
- Lord, Nick, "Quadrilaterals with area formula [math]\displaystyle{ \displaystyle K = \sqrt. }[/math]", Mathematical Gazette 96, July 2012, 345-347.
- Josefsson, Martin (2012), "Maximal Area of a Bicentric Quadrilateral", Forum Geometricorum 12: 237–241, http://forumgeom.fau.edu/FG2012volume12/FG201222.pdf .
- Alsina, Claudi; Nelsen, Roger (2009). When less is more: visualizing basic inequalities. Mathematical Association of America. pp. 64–66. ISBN 978-0-88385-342-9. https://archive.org/details/whenlessismorevi00alsi_112.
- Inequalities proposed in Crux Mathematicorum, 2007.[5]
- Josefsson, Martin (2012), "A New Proof of Yun’s Inequality for Bicentric Quadrilaterals", Forum Geometricorum 12: 79–82, http://forumgeom.fau.edu/FG2012volume12/FG201208.pdf .
- M. Radic, Z. Kaliman, and V. Kadum, "A condition that a tangential quadrilateral is also a chordal one", Mathematical Communications, 12 (2007) 33–52.
- Pop, Ovidiu T., "Identities and inequalities in a quadrilateral", Octogon Mathematical Magazine, Vol. 17, No. 2, October 2009, pp 754-763.
- Radic, Mirko, "Certain inequalities concerning bicentric quadrilaterals, hexagons and octagons", Journal of Inequalities in Pure and Applied Mathematics, Volume 6, Issue 1, 2005, [6]
- Hess, Albrecht (2014), "On a circle containing the incenters of tangential quadrilaterals", Forum Geometricorum 14: 389–396, http://forumgeom.fau.edu/FG2014volume14/FG201437.pdf .
- Yun, Zhang, "Euler's Inequality Revisited", Mathematical Spectrum, Volume 40, Number 3 (May 2008), pp. 119-121. First page available at [1] .
- Shattuck, Mark, “A Geometric Inequality for Cyclic Quadrilaterals”, Forum Geometricorum 18, 2018, 141-154. http://forumgeom.fau.edu/FG2018volume18/FG201822.pdf This paper also gives various inequalities in terms of the arc lengths subtended by a cyclic quadrilateral’s sides.
- Dörrie, Heinrich (1965). 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover. pp. 188–193. ISBN 978-0-486-61348-2.
- Salazar, Juan Carlos (2006), "Fuss's Theorem", Mathematical Gazette 90 (July): 306–307 .
- Byerly, W. E. (1909), "The In- and-Circumscribed Quadrilateral", The Annals of Mathematics 10: 123–128, doi:10.2307/1967103 . https://dx.doi.org/10.2307%2F1967103
- Calin, Ovidiu, Euclidean and Non-Euclidean Geometry a metric approach, [7], pp. 153–158.
- Bogomolny, Alex, Collinearity in Bicentric Quadrilaterals [8], 2004.
- Juan Carlos Salazar, Fuss Theorem for Bicentric Quadrilateral, 2003, [9].
- Crux Mathematicorum 34 (2008) no 4, p. 242.
- Post at Art of Problem Solving, 2009 http://www.artofproblemsolving.com/Forum/viewtopic.php?f=47&t=260539
- ALEXEY A. ZASLAVSKY, ONE PROPERTY OF BICENTRAL QUADRILATERAL, http://geometry.ru/olimp/2019/bicentr.pdf




