1. Definition

Power is the rate with respect to time at which work is done; it is the time derivative of work: [math]\displaystyle{ P =\frac{dW}{dt} }[/math] where P is power, W is work, and t is time.

If a constant force F is applied throughout a distance x, the work done is defined as [math]\displaystyle{ W = \mathbf{F} \cdot \mathbf{x} }[/math]. In this case, power can be written as: [math]\displaystyle{ P = \frac{dW}{dt} = \frac{d}{dt} \left(\mathbf{F} \cdot \mathbf{x}\right) = \mathbf{F}\cdot \frac{d\mathbf{x}}{dt} = \mathbf{F} \cdot \mathbf {v} }[/math]

If instead the force is variable over a three-dimensional curve C, then the work is expressed in terms of the line integral: [math]\displaystyle{ W = \int_C \mathbf{F} \cdot d\mathbf {r} = \int_{\Delta t} \mathbf{F} \cdot \frac{d\mathbf {r}}{dt} \ dt = \int_{\Delta t} \mathbf{F} \cdot \mathbf {v} \, dt }[/math]

From the fundamental theorem of calculus, we know that [math]\displaystyle{ P = \frac{dW}{dt} = \frac{d}{dt} \int_{\Delta t} \mathbf{F} \cdot \mathbf {v} \, dt = \mathbf{F} \cdot \mathbf {v}. }[/math] Hence the formula is valid for any general situation.

2. Units

The dimension of power is energy divided by time. In the International System of Units (SI), the unit of power is the watt (W), which is equal to one joule per second. Other common and traditional measures are horsepower (hp), comparing to the power of a horse; one mechanical horsepower equals about 745.7 watts. Other units of power include ergs per second (erg/s), foot-pounds per minute, dBm, a logarithmic measure relative to a reference of 1 milliwatt, calories per hour, BTU per hour (BTU/h), and tons of refrigeration.

3. Average Power

As a simple example, burning one kilogram of coal releases much more energy than detonating a kilogram of TNT,^[1] but because the TNT reaction releases energy much more quickly, it delivers far more power than the coal. If ΔW is the amount of work performed during a period of time of duration Δt, the average power P_avg over that period is given by the formula: [math]\displaystyle{ P_\mathrm{avg} = \frac{\Delta W}{\Delta t} }[/math] It is the average amount of work done or energy converted per unit of time. The average power is often simply called "power" when the context makes it clear.

The instantaneous power is then the limiting value of the average power as the time interval Δt approaches zero. [math]\displaystyle{ P = \lim_{\Delta t \to 0} P_\mathrm{avg} = \lim_{\Delta t \to 0} \frac{\Delta W}{\Delta t} = \frac{dW}{dt} }[/math]

In the case of constant power P, the amount of work performed during a period of duration t is given by: [math]\displaystyle{ W = Pt }[/math]

In the context of energy conversion, it is more customary to use the symbol E rather than W.

4. Mechanical Power

One metric horsepower is needed to lift 75 kilograms by 1 metre in 1 second. https://handwiki.org/wiki/index.php?curid=2043001

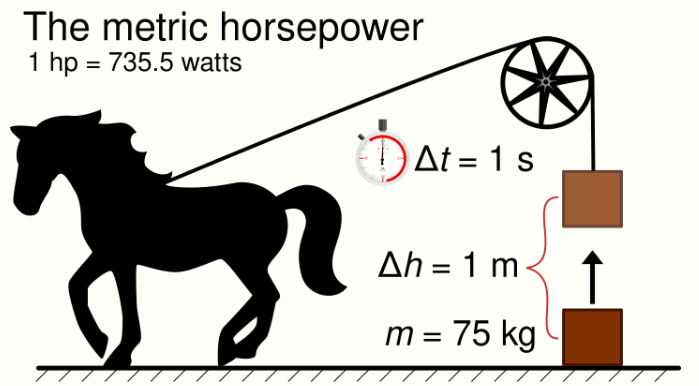
Power in mechanical systems is the combination of forces and movement. In particular, power is the product of a force on an object and the object's velocity, or the product of a torque on a shaft and the shaft's angular velocity.

Mechanical power is also described as the time derivative of work. In mechanics, the work done by a force F on an object that travels along a curve C is given by the line integral: [math]\displaystyle{ W_C = \int_C \mathbf{F} \cdot \mathbf{v} \, dt = \int_C \mathbf{F} \cdot d\mathbf{x} }[/math] where x defines the path C and v is the velocity along this path.

If the force F is derivable from a potential (conservative), then applying the gradient theorem (and remembering that force is the negative of the gradient of the potential energy) yields: [math]\displaystyle{ W_C = U(A) - U(B) }[/math] where A and B are the beginning and end of the path along which the work was done.

The power at any point along the curve C is the time derivative: [math]\displaystyle{ P(t) = \frac{dW}{dt} = \mathbf{F} \cdot \mathbf{v} = -\frac{dU}{dt} }[/math]

In one dimension, this can be simplified to: [math]\displaystyle{ P(t) = F \cdot v }[/math]

In rotational systems, power is the product of the torque τ and angular velocity ω, [math]\displaystyle{ P(t) = \boldsymbol{\tau} \cdot \boldsymbol{\omega} }[/math] where ω measured in radians per second. The [math]\displaystyle{ \cdot }[/math] represents scalar product.

In fluid power systems such as hydraulic actuators, power is given by [math]\displaystyle{ P(t) = pQ }[/math] where p is pressure in pascals, or N/m² and Q is volumetric flow rate in m³/s in SI units.

4.1. Mechanical Advantage

If a mechanical system has no losses, then the input power must equal the output power. This provides a simple formula for the mechanical advantage of the system.

Let the input power to a device be a force F_A acting on a point that moves with velocity v_A and the output power be a force F_B acts on a point that moves with velocity v_B. If there are no losses in the system, then [math]\displaystyle{ P = F_\text{B} v_\text{B} = F_\text{A} v_\text{A}, }[/math] and the mechanical advantage of the system (output force per input force) is given by [math]\displaystyle{ \mathrm{MA} = \frac{F_\text{B}}{F_\text{A}} = \frac{v_\text{A}}{v_\text{B}}. }[/math]

The similar relationship is obtained for rotating systems, where T_A and ω_A are the torque and angular velocity of the input and T_B and ω_B are the torque and angular velocity of the output. If there are no losses in the system, then [math]\displaystyle{ P = T_\text{A} \omega_\text{A} = T_\text{B} \omega_\text{B}, }[/math] which yields the mechanical advantage [math]\displaystyle{ \mathrm{MA} = \frac{T_\text{B}}{T_\text{A}} = \frac{\omega_\text{A}}{\omega_\text{B}}. }[/math]

These relations are important because they define the maximum performance of a device in terms of velocity ratios determined by its physical dimensions. See for example gear ratios.

5. Electrical Power

Ansel Adams photograph of electrical wires of the Boulder Dam Power Units, 1941–1942. https://handwiki.org/wiki/index.php?curid=1737111

The instantaneous electrical power P delivered to a component is given by [math]\displaystyle{ P(t) = I(t) \cdot V(t) }[/math] where

• [math]\displaystyle{ P(t) }[/math] is the instantaneous power, measured in watts (joules per second)
• [math]\displaystyle{ V(t) }[/math] is the potential difference (or voltage drop) across the component, measured in volts
• [math]\displaystyle{ I(t) }[/math] is the current through it, measured in amperes

If the component is a resistor with time-invariant voltage to current ratio, then: [math]\displaystyle{ P = I \cdot V = I^2 \cdot R = \frac{V^2}{R} }[/math] where [math]\displaystyle{ R = \frac{V}{I} }[/math] is the electrical resistance, measured in ohms.

6. Peak Power and Duty Cycle

In a train of identical pulses, the instantaneous power is a periodic function of time. The ratio of the pulse duration to the period is equal to the ratio of the average power to the peak power. It is also called the duty cycle (see text for definitions). https://handwiki.org/wiki/index.php?curid=1872683

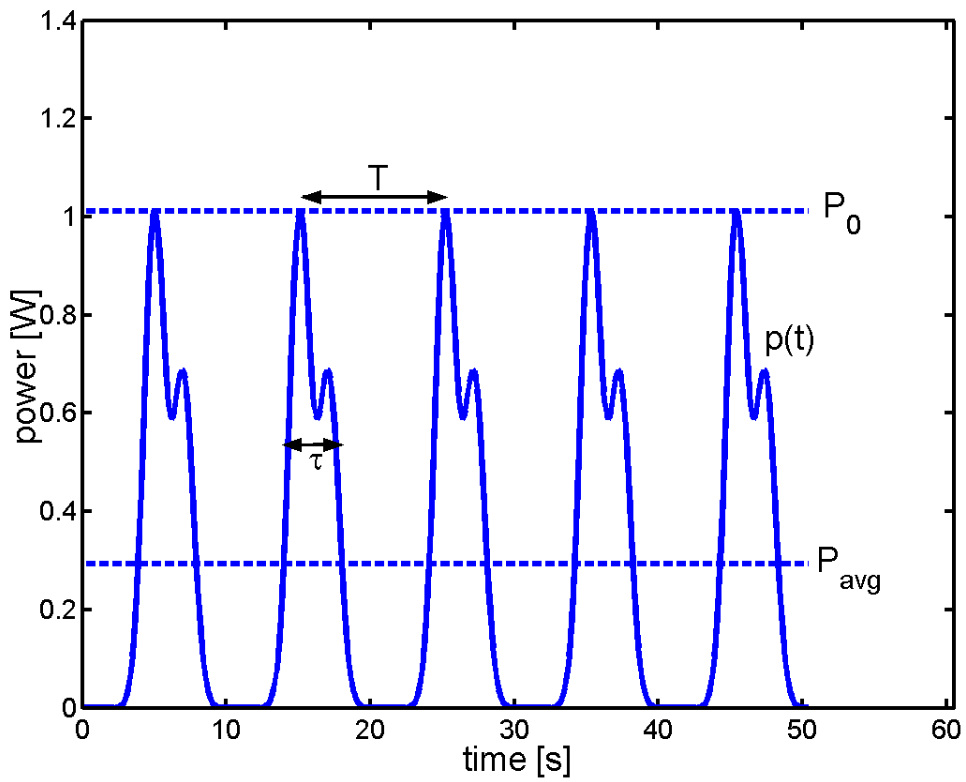
In the case of a periodic signal [math]\displaystyle{ s(t) }[/math] of period [math]\displaystyle{ T }[/math], like a train of identical pulses, the instantaneous power [math]\displaystyle{ p(t) = |s(t)|^2 }[/math] is also a periodic function of period [math]\displaystyle{ T }[/math]. The peak power is simply defined by: [math]\displaystyle{ P_0 = \max [p(t)] }[/math]

The peak power is not always readily measurable, however, and the measurement of the average power [math]\displaystyle{ P_\mathrm{avg} }[/math] is more commonly performed by an instrument. If one defines the energy per pulse as: [math]\displaystyle{ \varepsilon_\mathrm{pulse} = \int_0^T p(t) \, dt }[/math] then the average power is: [math]\displaystyle{ P_\mathrm{avg} = \frac{1}{T} \int_0^T p(t) \, dt = \frac{\varepsilon_\mathrm{pulse}}{T} }[/math]

One may define the pulse length [math]\displaystyle{ \tau }[/math] such that [math]\displaystyle{ P_0\tau = \varepsilon_\mathrm{pulse} }[/math] so that the ratios [math]\displaystyle{ \frac{P_\mathrm{avg}}{P_0} = \frac{\tau}{T} }[/math] are equal. These ratios are called the duty cycle of the pulse train.

7. Radiant Power

Power is related to intensity at a radius [math]\displaystyle{ r }[/math]; the power emitted by a source can be written as: [math]\displaystyle{ P(r) = I(4\pi r^2) }[/math]