
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Sirius Huang | -- | 2597 | 2022-10-26 01:45:35 | | | |
| 2 | Sirius Huang | Meta information modification | 2597 | 2022-10-31 09:25:37 | | |
Video Upload Options
The derivation of the Forouhi–Bloomer dispersion equations is based on obtaining an expression for k as a function of photon energy, symbolically written as k(E), starting from first principles quantum mechanics and solid state physics. An expression for n as a function of photon energy, symbolically written as n(E), is then determined from the expression for k(E) in accordance to the Kramers–Kronig relations which states that n(E) is the Hilbert Transform of k(E). The Forouhi–Bloomer dispersion equations for n(E) and k(E) of amorphous materials are given as: [math]\displaystyle{ k(E) = \frac{A(E-E_g)^2}{E^2-BE+C} \ }[/math] [math]\displaystyle{ n(E) = n(\infty)+\frac{(B_0 E + C_0 )}{E^2-BE+C} \ }[/math] The five parameters A, B, C, Eg, and n(∞) each have physical significance. Eg is the optical energy band gap of the material. A, B, and C depend on the band structure of the material. They are positive constants such that 4C-B2 > 0. Finally, n(∞), a constant greater than unity, represents the value of n at E = ∞. The parameters B0 and C0 in the equation for n(E) are not independent parameters, but depend on A, B, C, and Eg. They are given by: [math]\displaystyle{ B_0 = \frac{A}{Q} \ \left (\frac{-B^2}{2} \ + E_gB - {E_g}^2 + C \right) }[/math] [math]\displaystyle{ C_0 = \frac{A}{Q} \ \left [({E_g}^2 + C) \frac{B}{2} \ - 2E_g C \right] }[/math] where [math]\displaystyle{ Q = \frac{1}{2} \ (4C - B^2 )^{\frac{1}{2}} }[/math] Thus, for amorphous materials, a total of five parameters are sufficient to fully describe the dependence of both n and k on photon energy, E. For crystalline materials which have multiple peaks in their n and k spectra, the Forouhi–Bloomer dispersion equations can be extended as follows: [math]\displaystyle{ k(E) = \sum_{i=1}^q \left [\frac{A_i(E - E_{g_i})^2}{E^2-B_iE+C_i} \right] }[/math] [math]\displaystyle{ n(E) = n(\infty)+\sum_{i=1}^q \left [\frac{B_{0_i}E+C_{0_i}}{E^2-B_iE+C_i} \right] }[/math] The number of terms in each sum, q, is equal to the number of peaks in the n and k spectra of the material. Every term in the sum has its own values of the parameters A, B, C, Eg, as well as its own values of B0 and C0. Analogous to the amorphous case, the terms all have physical significance.
1. Characterizing Thin Films
The refractive index (n) and extinction coefficient (k) are related to the interaction between a material and incident light, and are associated with refraction and absorption (respectively). They can be considered as the “fingerprint of the material". Thin film material coatings on various substrates provide important functionalities for the microfabrication industry, and the n, k, as well as the thickness, t, of these thin film constituents must be measured and controlled to allow for repeatable manufacturing.
The Forouhi–Bloomer dispersion equations for n and k were originally expected to apply to semiconductors and dielectrics, whether in amorphous, polycrystalline, or crystalline states. However, they have been shown to describe the n and k spectra of transparent conductors,[1] as well as metallic compounds.[2][3][4][5][6][7][8][9][10][11] The formalism for crystalline materials was found to also apply to polymers,[12][13][14] which consist of long chains of molecules that do not form a crystallographic structure in the classical sense.
Other dispersion models that can be used to derive n and k, such as Tauc-Lorentz, can be found in the literature.[15][16] Two well-known models—Cauchy and Sellmeier—provide empirical expressions for n valid over a limited measurement range, and are only useful for non-absorbing films where k=0. Consequently, the Forouhi–Bloomer formulation has been used for measuring thin films in various applications.[1][2][3][4][5][6][7][8][9][10][11][12][13][14][15][16]
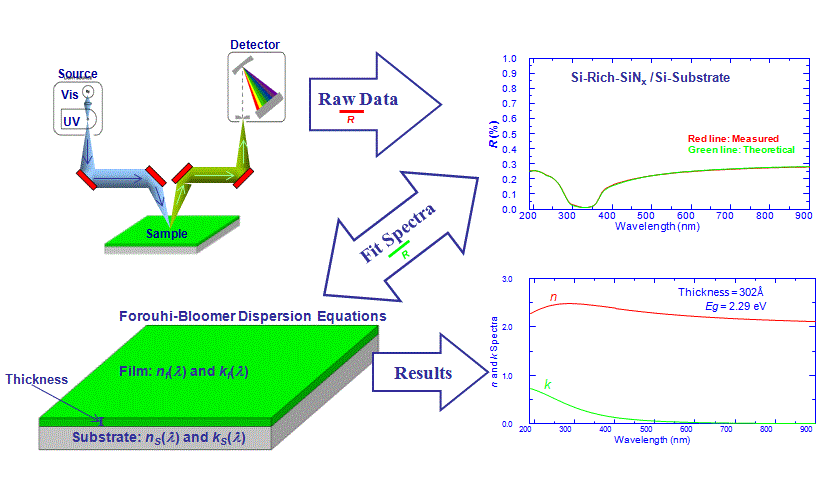
In the following discussions, all variables of photon energy, E, will be described in terms of wavelength of light, λ, since experimentally variables involving thin films are typically measured over a spectrum of wavelengths. The n and k spectra of a thin film cannot be measured directly, but must be determined indirectly from measurable quantities that depend on them. Spectroscopic reflectance, R(λ), is one such measurable quantity. Another, is spectroscopic transmittance, T(λ), applicable when the substrate is transparent. Spectroscopic reflectance of a thin film on a substrate represents the ratio of the intensity of light reflected from the sample to the intensity of incident light, measured over a range of wavelengths, whereas spectroscopic transmittance, T(λ), represents the ratio of the intensity of light transmitted through the sample to the intensity of incident light, measured over a range of wavelengths; typically, there will also be a reflected signal, R(λ), accompanying T(λ).
The measurable quantities, R(λ) and T(λ) depend not only on n(λ) and k(λ) of the film, but also on film thickness, t, and n(λ) and k(λ) of the substrate. For a silicon substrate, the n(λ) and k(λ) values are known and are taken as a given input. The challenge of characterizing thin films involves extracting t, n(λ) and k(λ) of the film from the measurement of R(λ) and/or T(λ). This can be achieved by combining the Forouhi–Bloomer dispersion equations for n(λ) and k(λ) with the Fresnel equations for the reflection and transmission of light at an interface[17] to obtain theoretical, physically valid, expressions for reflectance and transmittance. In so doing, the challenge is reduced to extracting the five parameters A, B, C, Eg, and n(∞) that constitute n(λ) and k(λ), along with film thickness, t, by utilizing a nonlinear least squares regression analysis[18][19] fitting procedure. The fitting procedure entails an iterative improvement of the values of A, B, C, Eg, n(∞), t, in order to reduce the sum of the squares of the errors between the theoretical R(λ) or theoretical T(λ) and the measured spectrum of R(λ) or T(λ).
Besides spectroscopic reflectance and transmittance, spectroscopic ellipsometry can also be used in an analogous way to characterize thin films and determine t, n(λ) and k(λ).
2. Measurement Examples
The following examples show the versatility of using the Forouhi–Bloomer dispersion equations to characterize thin films utilizing a tool based on near-normal incident spectroscopic reflectance. Near-normal spectroscopic transmittance is also utilized when the substrate is transparent. The n(λ) and k(λ) spectra of each film are obtained along with film thickness, over a wide range of wavelengths from deep ultraviolet to near infrared wavelengths (190–1000 nm).
In the following examples, the notation for theoretical and measured reflectance in the spectral plots is expressed as “R-theor” and “R-meas”, respectively.
Below are schematics depicting the thin film measurement process:
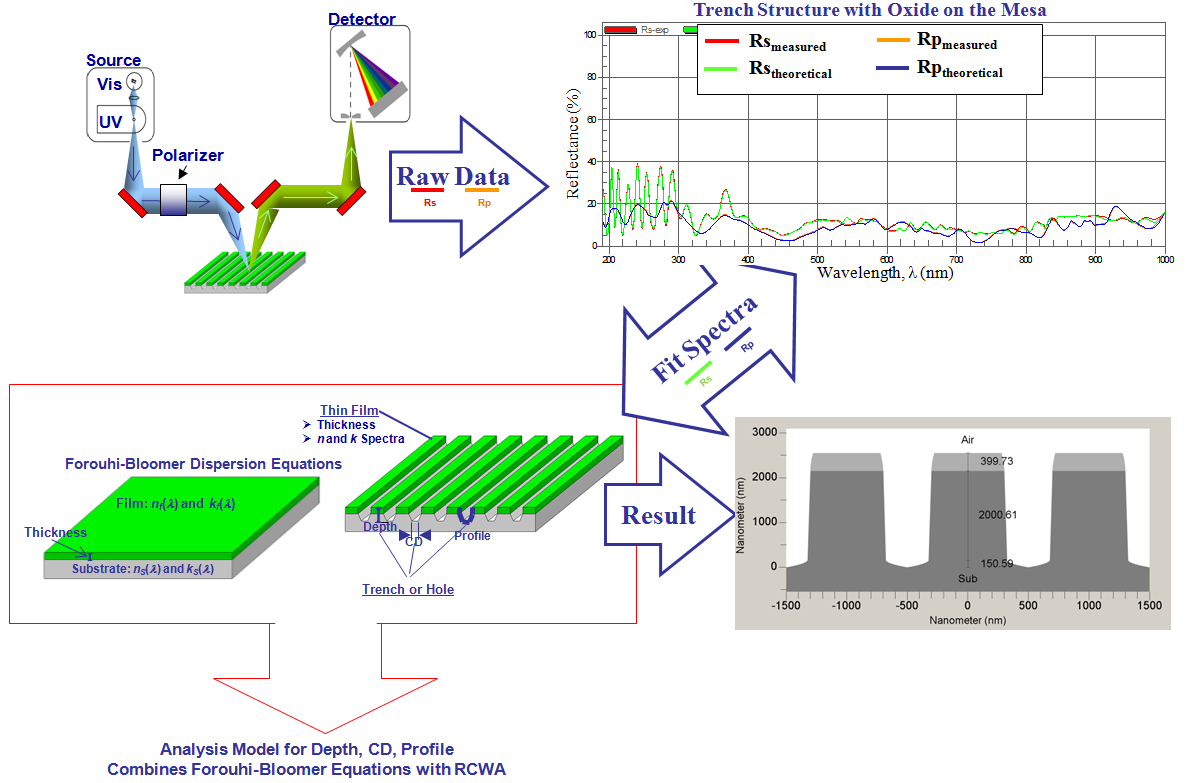
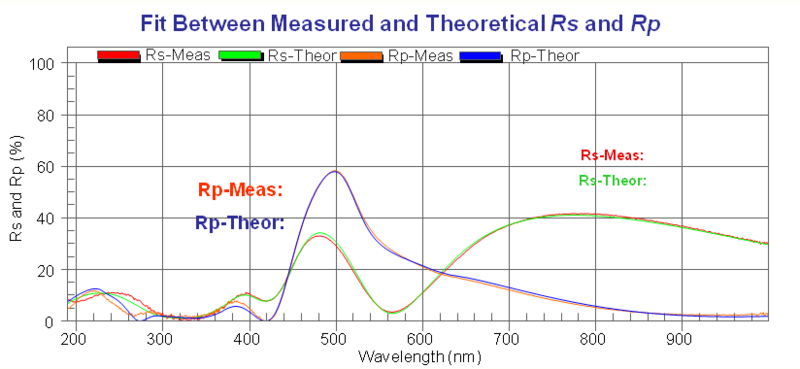
The Forouhi–Bloomer dispersion equations in combination with Rigorous Coupled-Wave Analysis (RCWA) have also been used to obtain detailed profile information (depth, CD, sidewall angle) of trench structures. In order to extract structure information, polarized broadband reflectance data, Rs and Rp, must be collected over a large wavelength range from a periodic structure (grating), and then analyzed with a model that incorporates Forouhi–Bloomer dispersion equations and RCWA. Inputs into the model include grating pitch and n and k spectra of all materials within the structure, while outputs can include Depth, CDs at multiple locations, and even sidewall angle. The n and k spectra of such materials can be obtained in accordance with the methodology described in this section for thin film measurements.
Below are schematics depicting the measurement process for trench structures. Examples of trench measurements then follow.
2.1. Example 1: Amorphous Silicon on Oxidized Silicon Substrate (a-Si/SiO2/Si-Sub)
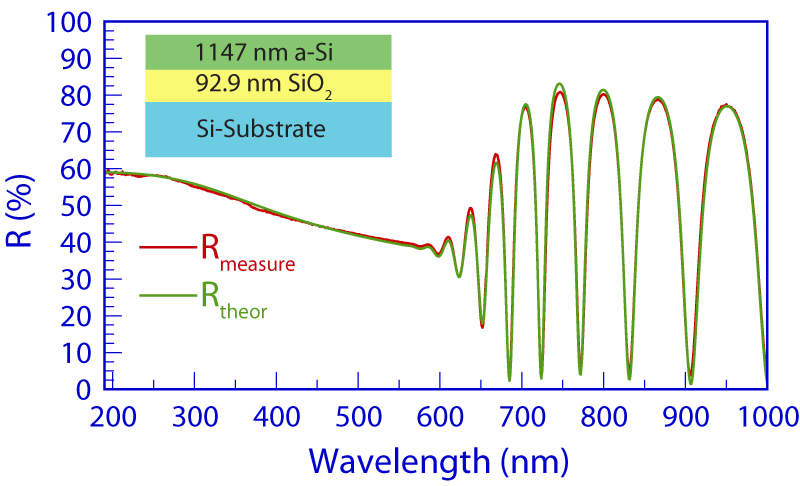
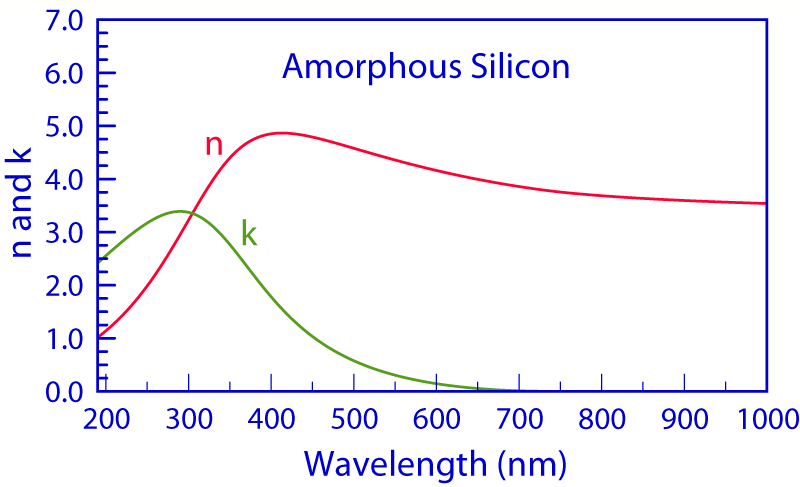
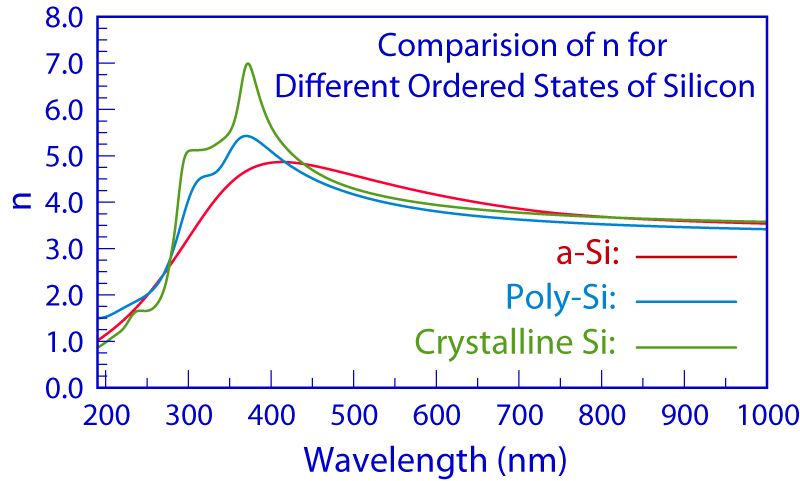
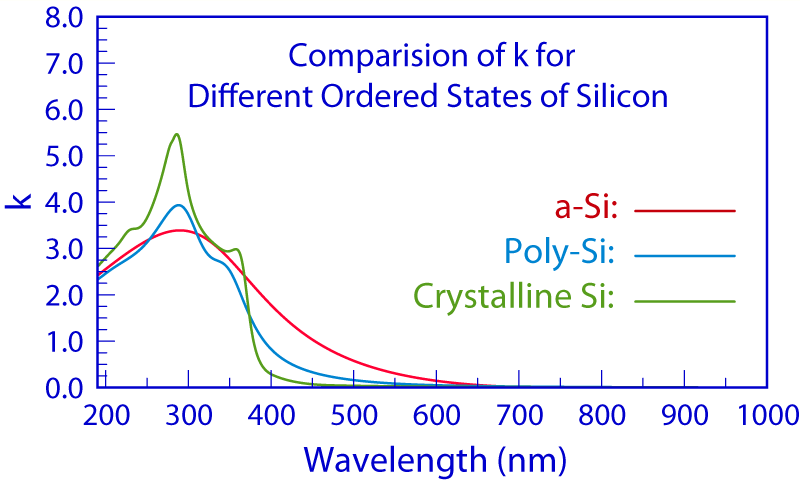
Example 1 shows one broad maximum in the n(λ) and k(λ) spectra of the a-Si film, as is expected for amorphous materials. As a material transitions toward crystallinity, the broad maximum gives way to several sharper peaks in its n(λ) and k(λ) spectra, as demonstrated in the graphics.
When the measurement involves two or more films in a stack of films, the theoretical expression for reflectance must be expanded to include the n(λ) and k(λ) spectra, plus thickness, t, of each film. However, the regression may not converge to unique values of the parameters, due to the non-linear nature of the expression for reflectance. So it is helpful to eliminate some of the unknowns . For example, the n(λ) and k(λ) spectra of one or more of the films may be known from the literature or previous measurements, and held fixed (not allowed to vary) during the regression. To obtain the results shown in Example 1, the n(λ) and k(λ) spectra of the SiO2 layer was fixed, and the other parameters, n(λ) and k(λ) of a-Si, plus thicknesses of both a-Si and SiO2 were allowed to vary.
2.2. Example 2: 248 nm Photoresist on Silicon Substrate (PR/Si-Sub)
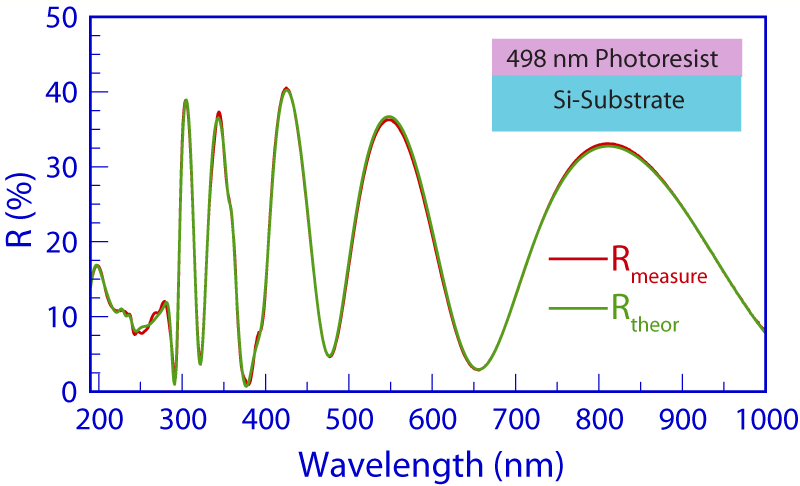
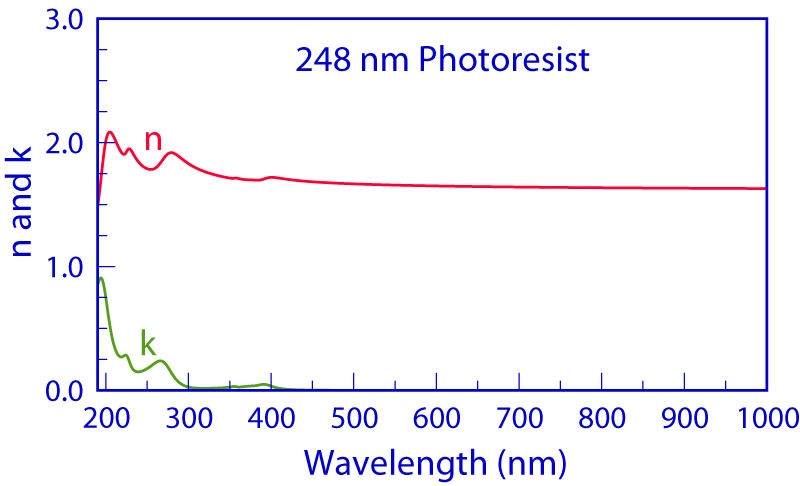
Polymers such as photoresist consist of long chains of molecules which do not form a crystallographic structure in the classic sense. However, their n(λ) and k(λ) spectra exhibit several sharp peaks rather than a broad maximum expected for non-crystalline materials. Thus, the measurement results for a polymer are based on the Forouhi–Bloomer formulation for crystalline materials. Most of the structure in the n(λ) and k(λ) spectra occurs in the deep UV wavelength range and thus to properly characterize a film of this nature, it is necessary that the measured reflectance data in the deep UV range is accurate.
The figure shows a measurement example of a photoresist (polymer) material used for 248 nm micro-lithography. Six terms were used in the Forouhi–Bloomer equations for crystalline materials to fit the data and achieve the results.
2.3. Example 3: Indium Tin Oxide on Glass Substrate (ITO/Glass-Sub)
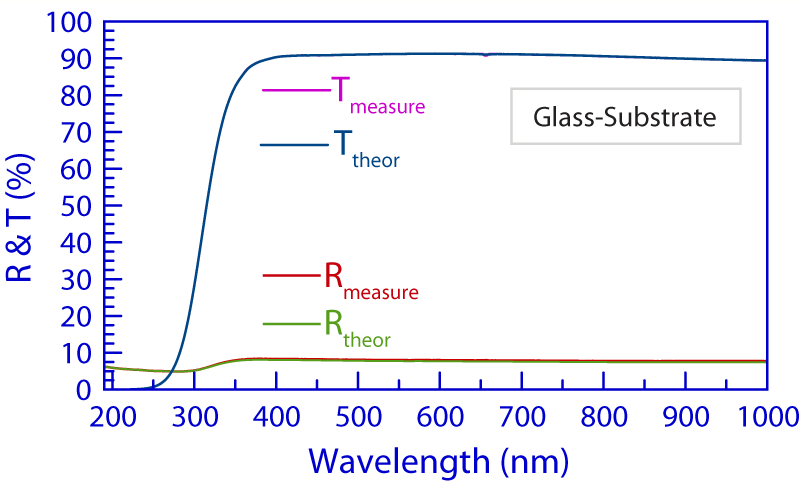
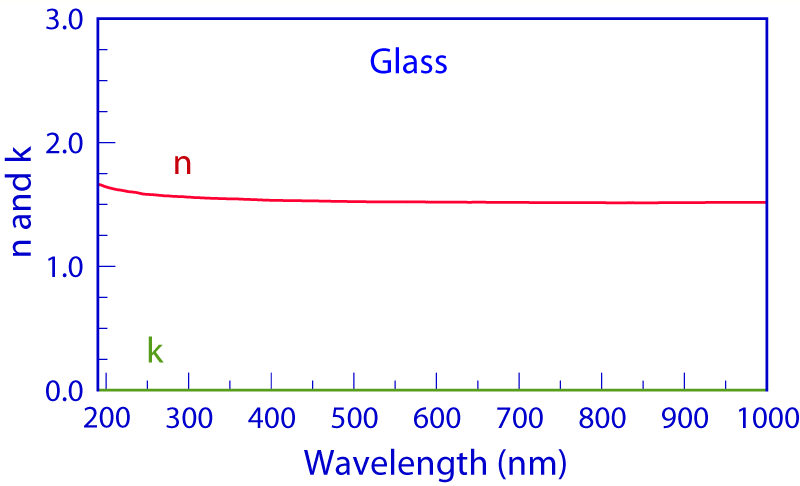
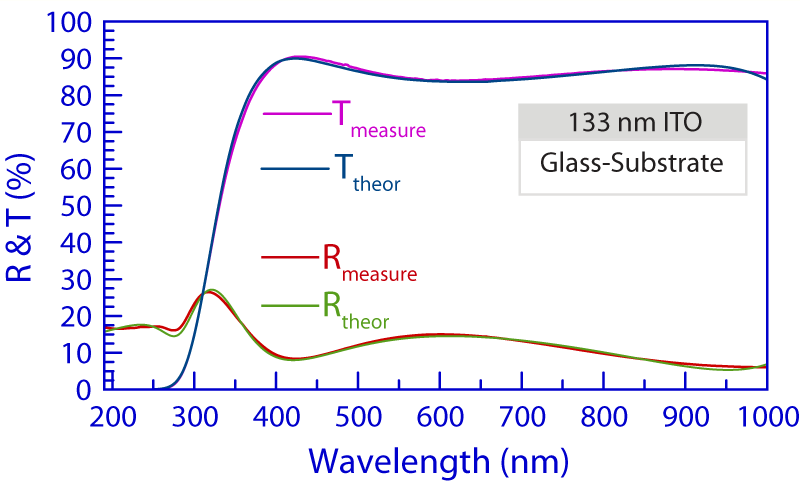
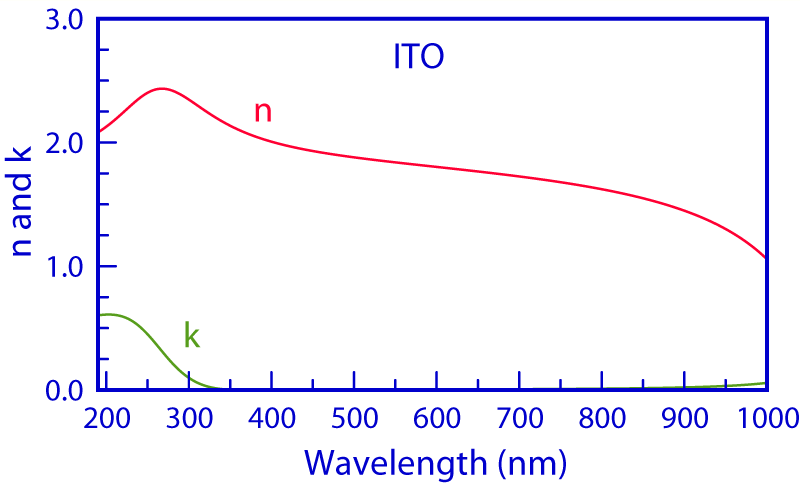
Indium tin oxide (ITO) is a conducting material with the unusual property that it is transparent, so it is widely used in the flat panel display industry. Reflectance and transmittance measurements of the uncoated glass substrate were needed in order to determine the previously unknown n(λ) and k(λ) spectra of the glass. The reflectance and transmittance of ITO deposited on the same glass substrate were then measured simultaneously, and analyzed using the Forouhi–Bloomer equations.
As expected, the k(λ) spectrum of ITO is zero in the visible wavelength range, since ITO is transparent. The behavior of the k(λ) spectrum of ITO in the near-infrared (NIR) and infrared (IR) wavelength ranges resembles that of a metal: non-zero in the NIR range of 750–1000 nm (difficult to discern in the graphics since its values are very small) and reaching a maximum value in the IR range (λ>1000 nm). The average k value of the ITO film in the NIR and IR range is 0.05.
2.4. Example 4: Multi-Spectral Analysis of Germanium (40%)–Selenium (60%) Thin Films
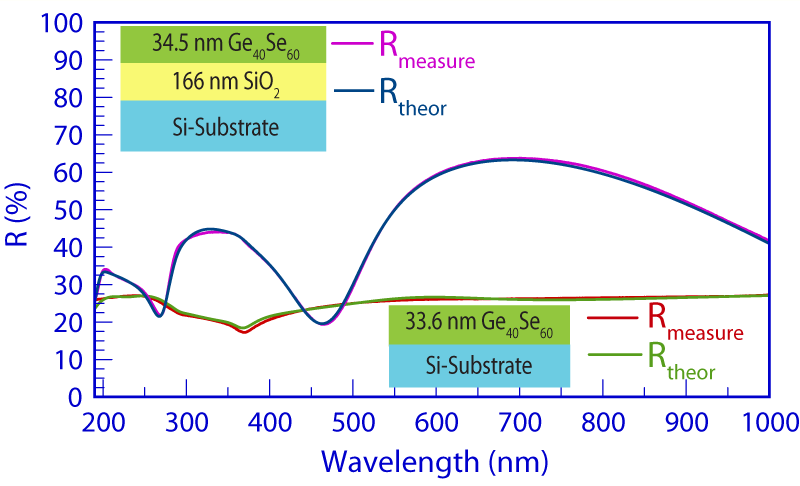
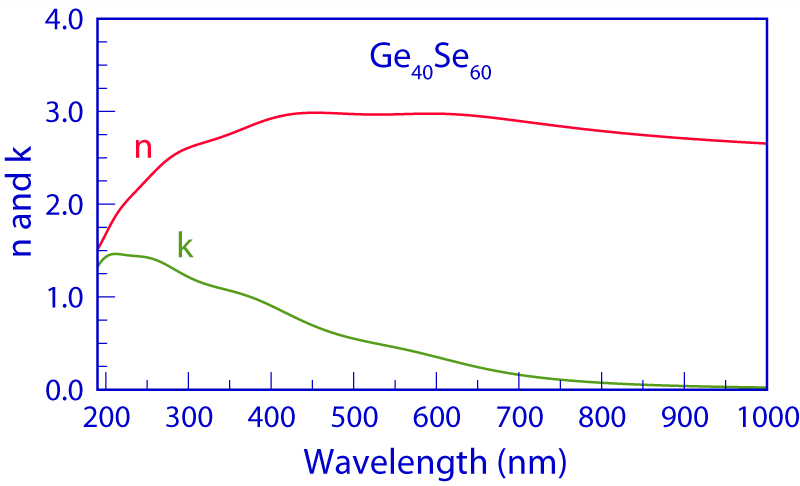
When dealing with complex films, in some instances the parameters cannot be resolved uniquely. To constrain the solution to a set of unique values, a technique involving multi-spectral analysis can be used. In the simplest case, this entails depositing the film on two different substrates and then simultaneously analyzing the results using the Forouhi–Bloomer dispersion equations.
For example, the single measurement of reflectance in 190–1000 nm range of Ge40Se60/Si does not provide unique n(λ) and k(λ) spectra of the film. However, this problem can be solved by depositing the same Ge40Se60 film on another substrate, in this case oxidized silicon, and then simultaneously analyzing the measured reflectance data to determine:
-
- Thickness of the Ge40Se60/Si film on the silicon substrate as 34.5nm,
- Thickness of the Ge40Se60/Si film on the oxidized silicon substrate as 33.6nm,
- Thickness of SiO2 (with n and k spectra of SiO2 held fixed), and
- n and k spectra, in 190–1000 nm range, of Ge40Se60/Si.
2.5. Example 5: Complex Trench Structure
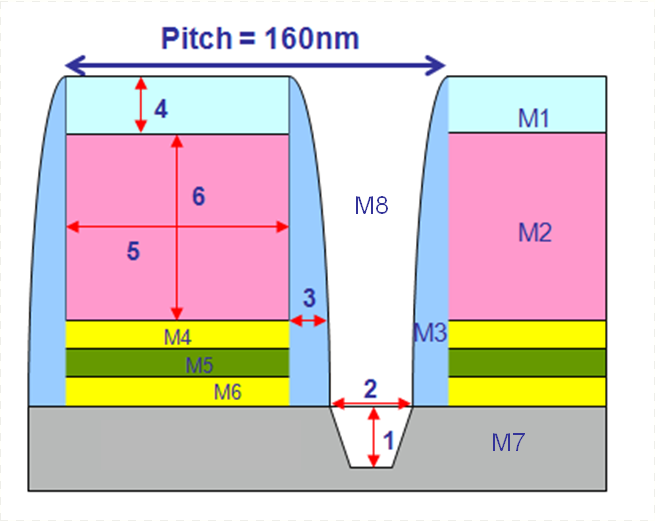
The trench structure depicted in the adjacent diagram repeats itself in 160 nm intervals, that is, it has a given pitch of 160 nm. The trench is composed of the following materials:
Accurate n and k values of these materials are necessary in order to analyze the structure. Often a blanket area on the trench sample with the film of interest is present for the measurement. In this example, the reflectance spectrum of the poly-silicon was measured on a blanket area containing the poly-silicon, from which its n and k spectra were determined in accordance with the methodology described in this article that utilizes the Forouhi–Bloomer dispersion equations. Fixed tables of n and k values were used for the SiO2 and Si3N4 films.
Combining the n and k spectra of the films with Rigorous Coupled-Wave Analysis (RCWA) the following critical parameters were determined (with measured results as well):
| Measured Parameter | Results | |
|---|---|---|
| 1 | Si Depth | 27.4 nm |
| 2 | CD @ Top of Si | 26.4 nm |
| 3 | SiO2 Liner Width | 40.2 nm |
| 4 | Si3N4 Height | 28 nm |
| 3 | Poly-Si Width | 92.6 nm |
| 3 | Poly-Si Height | 85.6 nm |
References
- Torkaman, N.M.; Ganjkhanlou, Y.; Kazemzad, M.; Dabaghi, H.H.; Keyanpour-Rad, M. (2010). "Crystallographic Parameters and Electro-Optical Constants in ITO Thin Films". Materials Characterization 61 (3): 362–370. doi:10.1016/j.matchar.2009.12.020. https://dx.doi.org/10.1016%2Fj.matchar.2009.12.020
- Lakhdar, M.H.; Ouni, B.; Amlouk, M. (2014). "Thickness Effect on the Structural and Optical Constants of Stibnite Thin Films Prepared by Sulfidation Annealing of Antimony Films". Optik – International Journal for Light and Electron Optics.
- Al-Khanbashi, H.A.; Shirbeeny, W.; Al-Ghamdi, A.A.; Bronstein, L.M.; Mahmoud, W.E. (2014). "Spectroscopic Ellipsometry of Zn1−xCuxO Thin Films Based on a Modified Sol–Gel Dip-Coating Technique". Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy 118: 800–805. doi:10.1016/j.saa.2013.09.085. PMID 24157332. Bibcode: 2014AcSpA.118..800A. https://dx.doi.org/10.1016%2Fj.saa.2013.09.085
- Nakamura, T.; Moriyama, T.; Nabatova-Gabain, N.; Adachi, S. (2014). "Emission Decay Rate of a Light Emitter on Thin Metal Films". Japanese Journal of Applied Physics 53 (4): 5201. doi:10.7567/jjap.53.045201. Bibcode: 2014JaJAP..53d5201N. https://dx.doi.org/10.7567%2Fjjap.53.045201
- Winkler, M.T.; Wang, W.; Gunawan, O.; Hovel, H.J.; Todorova, T.K.; Mitzi, D.B. (2014). "Optical Designs that Improve the Efficiency of Cu2ZnSn(S,Se)4 Solar Cells". Energy & Environmental Science 7 (3): 1029–1036. doi:10.1039/c3ee42541j. https://dx.doi.org/10.1039%2Fc3ee42541j
- Miao, L.; Su, L.F.; Tanemura, S.; Fisher, C.A.J.; Zhao, L.L.; Liang, Q.; Xu, G. (2013). "Cost-Effective Nanoporous SiO2–TiO2 Coatings on Glass Substrates with Antireflective and Self-Cleaning Properties". Applied Energy 112: 1198–1205. doi:10.1016/j.apenergy.2013.03.043. https://dx.doi.org/10.1016%2Fj.apenergy.2013.03.043
- Zhang, F.; Zhang, R.J.; Zhang, D.X.; Wang, Z.Y.; Xu, J.P.; Zheng, Y.X.; Chen, L.Y.; Huang, R.Z. et al. (2013). "Temperature-Dependent Optical Properties of Titanium Oxide Thin Films Studied by Spectroscopic Ellipsometry". Applied Physics Express 6 (12): 121101. doi:10.7567/apex.6.121101. Bibcode: 2013APExp...6l1101Z. https://dx.doi.org/10.7567%2Fapex.6.121101
- Sheng-Hong, Y.; Sen, C.; Ning, Y.; Yue-Li, Z. (2013). "Optical Study of Sol-gel Processed Nd-doped BiFeO3 Multiferroic Films by Spectroscopic Ellipsometry". Ferroelectrics 454 (1): 78–83. doi:10.1080/00150193.2013.842802. https://dx.doi.org/10.1080%2F00150193.2013.842802
- Balakrishnan, G.; Sundari, S.T.; Kuppusami, P.; Chandra, P.M.; Srinivasan, M.P.; Mohandas, E.; Ganesan, V.; Sastikumar, D. (2011). "A Study of Microstructural and Optical Properties of Nanocrystalline Ceria Thin Films Prepared by Pulsed Laser Deposition". Thin Solid Films 519 (8): 2520–2526. doi:10.1016/j.tsf.2010.12.013. Bibcode: 2011TSF...519.2520B. https://dx.doi.org/10.1016%2Fj.tsf.2010.12.013
- Cheng, K.W.; Huang, C.M.; Pan, G.T.; Chang, W.S.; Lee, T.C.; Yang, T.C.K. (2010). "Effect of Sb on the growth and photoelectrochemical response of AgIn5S8 Film Electrodes Created by Solution Growth Technique". Chemical Engineering Science 65 (1): 74–79. doi:10.1016/j.ces.2009.02.002. https://dx.doi.org/10.1016%2Fj.ces.2009.02.002
- Das, N.S.; Ghosh, P.K.; Mitra, M.K.; Chattopadhyay, K.K. (2010). "Effect of Film Thickness on the Energy Band Gap of Nanocrystalline CdS Thin Films Analyzed by Spectroscopic Ellipsometry". Physica E: Low-dimensional Systems and Nanostructures 42 (8): 2097–2102. doi:10.1016/j.physe.2010.03.035. Bibcode: 2010PhyE...42.2097D. https://dx.doi.org/10.1016%2Fj.physe.2010.03.035
- Xiong, K.; Hou, L.; Wang, P.; Xia, Y.; Chen, D.; Xiao, B. (2014). "Phosphor-Doping Enhanced Efficiency in Bilayer Organic Solar Cells due to Longer Exciton Diffusion Length". Journal of Luminescence 151: 193–196. doi:10.1016/j.jlumin.2014.02.016. Bibcode: 2014JLum..151..193X. https://dx.doi.org/10.1016%2Fj.jlumin.2014.02.016
- Huynh, T.P.; Pietrzyk-Le, A.; Chandra-Bikram, K.C.; Noworyta, K.R.; Sobczak, J.W.; Sharma, P.S.; D'Souza, F.; Kutner, W. (2013). "Electrochemically Synthesized Molecularly Imprinted Polymer of Thiophene Derivatives for Flow-Injection Analysis Determination of Adenosine-5′-Triphosphate (ATP)". Biosensors and Bioelectronics 41: 634–641. doi:10.1016/j.bios.2012.09.038. PMID 23131778. https://dx.doi.org/10.1016%2Fj.bios.2012.09.038
- Zhu, D.; Shen, W.; Ye, H.; Liu, X.; Zhen, H. (2008). "Determination of the Optical Constants of Polymer Light-Emitting Diode Films from Single Reflection Measurements". Journal of Physics D: Applied Physics. 23 41 (23): 235104. doi:10.1088/0022-3727/41/23/235104. Bibcode: 2008JPhD...41w5104Z. https://dx.doi.org/10.1088%2F0022-3727%2F41%2F23%2F235104
- Laidani, N.; Bartali, R.; Gottardi, G.; Anderle, M.; Cheyssac, P. (2008). "Optical Absorption Parameters of Amorphous Carbon Films from Forouhi–Bloomer and Tauc–Lorentz Models: A Comparative Study". Journal of Physics: Condensed Matter 20 (1): 15216. doi:10.1088/0953-8984/20/01/015216. Bibcode: 2008JPCM...20a5216L. https://dx.doi.org/10.1088%2F0953-8984%2F20%2F01%2F015216
- Easwarakhanthan, T.; Beyssen, D.; Brizoual, L.L.; Alnot, P. (2007). "Forouhi–Bloomer and Tauc–Lorentz Optical Dispersions Applied Using Spectroscopic Ellipsometry to Plasma-Deposited Fluorocarbon Films". Journal of Applied Physics 101 (7): 073102–073102–7. doi:10.1063/1.2719271. Bibcode: 2007JAP...101g3102E. https://dx.doi.org/10.1063%2F1.2719271
- Heavens, O.S. (1965). Optical Properties of Thin Solid Films. New York: Dover.
- Levenberg, K. (1944). "A Method for the Solution of Certain Non-Linear Problems in Least Squares". The Quarterly of Applied Mathematics 2 (2): 164. doi:10.1090/qam/10666. https://dx.doi.org/10.1090%2Fqam%2F10666
- Marquardt, D.W. (1963). "An Algorithm for Least-Squares Estimation of Nonlinear Parameters". Journal of the Society for Industrial and Applied Mathematics. 2 11 (2): 431–441. doi:10.1137/0111030. https://dx.doi.org/10.1137%2F0111030




