Your browser does not fully support modern features. Please upgrade for a smoother experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Chengyi Song | -- | 2049 | 2022-10-28 12:56:39 | | | |
| 2 | Dean Liu | Meta information modification | 2049 | 2022-10-31 02:33:08 | | | | |
| 3 | Dean Liu | -23 word(s) | 2026 | 2022-10-31 02:37:01 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Xing, W.; Xu, Y.; Song, C.; Deng, T. Heat Dissipation Model of TIMs in High-Power Electronics. Encyclopedia. Available online: https://encyclopedia.pub/entry/31814 (accessed on 15 January 2026).
Xing W, Xu Y, Song C, Deng T. Heat Dissipation Model of TIMs in High-Power Electronics. Encyclopedia. Available at: https://encyclopedia.pub/entry/31814. Accessed January 15, 2026.
Xing, Wenkui, Yue Xu, Chengyi Song, Tao Deng. "Heat Dissipation Model of TIMs in High-Power Electronics" Encyclopedia, https://encyclopedia.pub/entry/31814 (accessed January 15, 2026).
Xing, W., Xu, Y., Song, C., & Deng, T. (2022, October 28). Heat Dissipation Model of TIMs in High-Power Electronics. In Encyclopedia. https://encyclopedia.pub/entry/31814
Xing, Wenkui, et al. "Heat Dissipation Model of TIMs in High-Power Electronics." Encyclopedia. Web. 28 October, 2022.
Copy Citation
To improve the heat dissipation capability of high-power electronic systems, advanced thermal interface materials (TIMs) with high thermal conductivity and low interfacial thermal resistance are urgently needed in the structural design of advanced electronics. Metal-, carbon- and polymer-based TIMs can reach high thermal conductivity and are promising for heat dissipation in high-power electronics.
thermal interface materials
thermal conductivity
high-power electronics
1. Introduction
Due to the highly integrated and hierarchical structure of high-power density electronics, there is tremendous localized thermal energy generated per unit time, which indicates advanced thermal management is necessary to reach higher stipulations of heat dissipation [1][2][3][4]. Effective thermal management could guarantee normal operation and efficient device performance, especially for high-power electronics with heat fluxes of 150–200 W·cm−2 and pulsed transient heat loads with fluxes of more than 400 W·cm−2 [5], such as automotive vehicles [6], defense electronics [7], aerospace [8] and computer processors [9]. Structural cooling systems such as microchannels for liquid cooling have been widely applied in electronics for effective heat dissipation [10][11]. The convection flow in microchannels contributes to the cooling process by removing the generated heat from electronics. For more integrated equipment with a smaller size and less operation space, air cooling can also be used in the high-power electronic system by adding cooling sinks into the electronic devices [12].
Usually, the contact between the chip and the cooling sink is not ideal due to the roughness of both materials at the microscale. Therefore, air with low thermal conductivity of only 0.024 W·m−1·K−1 always fills the spaces between the interfaces, resulting in high thermal contact resistance. Therefore, the implementation of advanced thermal interface materials (TIMs) plays a critical role in the effective thermal management of high-power electronics. TIMs are used to improve heat dissipation efficiency in electronic devices and are usually positioned between the chip and heat sink. They can fit well with the interfaces and eliminate air voids by filling the air gap between the chip and heat sink. Therefore, high thermal conductive TIMs should enhance heat transfer and reduce the thermal contact resistance. Additionally, TIMs require appropriate thermal expansion to match the working chips to minimize interfacial thermal resistance. As a result, the development of advanced TIMs and improvement in their thermal conductivity are of vital importance in the manufacture process of high-performance electronic devices. There are numerous types of TIMs commercially available or under development, including thermal grease/paste, carbon-based materials, phase change materials and filled polymers, which are suitable for employment in various kinds of electronic devices [13]. Low interfacial thermal resistance and high thermal conductivity, good adhesion and conformability are the general requirements for TIMs. Furthermore, TIMs should also have long-term stability, be nontoxic and not spill to keep pace with high-power electronic system technologies.
2. Heat Dissipation Model of TIMs Used in High-Power Electronics
Decreasing interfacial thermal resistance and enhancing the intrinsic thermal conductivity of TIMs are both effective methods to improve heat dissipation efficiency. Most TIMs are composites; therefore, it is of great significance to understand their heat conduction and dissipation models.
2.1. Thermal Resistance Models
During the heat dissipation of high-power electronic devices, heat flows from the high-temperature part to the low-temperature part. Thermal contact resistance (also known as Kapitza resistance) occurs between the solid substrate and TIMs, which impedes the propagation of heat flow. Apart from that, filler–filler and filler–matrix thermal contact resistance inside TIMs should also be considered for the whole system. The nanoscale fillers in the TIMs would introduce more interfaces, which would cause intense phonon scattering and impede the process of heat transfer. As a result, the control and further study of thermal contact resistance are of great significance in the development of advanced TIMs.
For metal-based TIMs, the thermal contact resistance at metallic–metallic interfaces is mainly caused by the scattering of electrons influenced by lattice mismatching and defects. For other metallic–nonmetallic interfaces, both phonons and electrons could be the carriers for heat conduction. Zhou and Li [14] proposed a metallic–nonmetallic interfacial heat transfer model, which pointed out that heat could transfer through the phonon–phonon coupling, phonon–electron coupling, and electron–electron coupling processes between metallic particles, the polymer matrix and nonmetallic particles. The degree of competition between these three kinds of transportation processes would determine the value of the thermal contact resistance.
Recently, a variety of methods have been introduced for predicting thermal contact resistance, including theoretical models, atomistic methods and experimental measurement methods [15][16]. Regarding the basic theoretical models, Swartz and Pohl [17] introduced the acoustic mismatch model (AMM) and the diffuse mismatch model (DMM), both of which consider that the interface at both sides of two materials has continuity. For the AMM, the incident phonons conducting heat can be treated as plane waves, and possible scattering can be ignored, which mean this model only matches well with actual situations at low temperatures (T < 10 K). In contrast to the AMM, the DMM considers that all the incident phonons are completely scattered, and can predict thermal contact resistance at about T > 15 K, but it is not applicable at higher temperatures. More developments based on these two models have also been made. Prasher [18] modified the traditional AMM and considered the influence of the van der Waals force between the nanofiller–nanofiller and nanofiller–matrix. Hopkins and Norris [19] proposed a modified joint frequency diffuse mismatch model (JFDMM) based on the DMM, which includes the effect of inelastic scattering of phonons. Atomistic methods, such as the Boltzmann equation [20], molecular dynamics (MD) [21] and Green’s function [22], can also be used to study interfacial thermal transportation at the atomic scale by simulating the motivation of the hot carriers, and use basic potential functions to calculate the thermal contact resistance between different materials.
According to the schematic diagram of high-power electronics’ heat dissipation in Figure 1, the interfacial thermal resistance of TIMs (RTIM) can be shown as follows [23]:
where BLT refers to the bond line thickness of TIMs, kTIM refers to the thermal conductivity of TIMs, RC1 is the thermal contact resistance between the TIM and the heat sink, and RC2 is the thermal contact resistance between the TIM and the chip. This formula shows that TIMs with lower BLT and higher thermal conductivity are ideal for achieving lower interfacial thermal resistance.
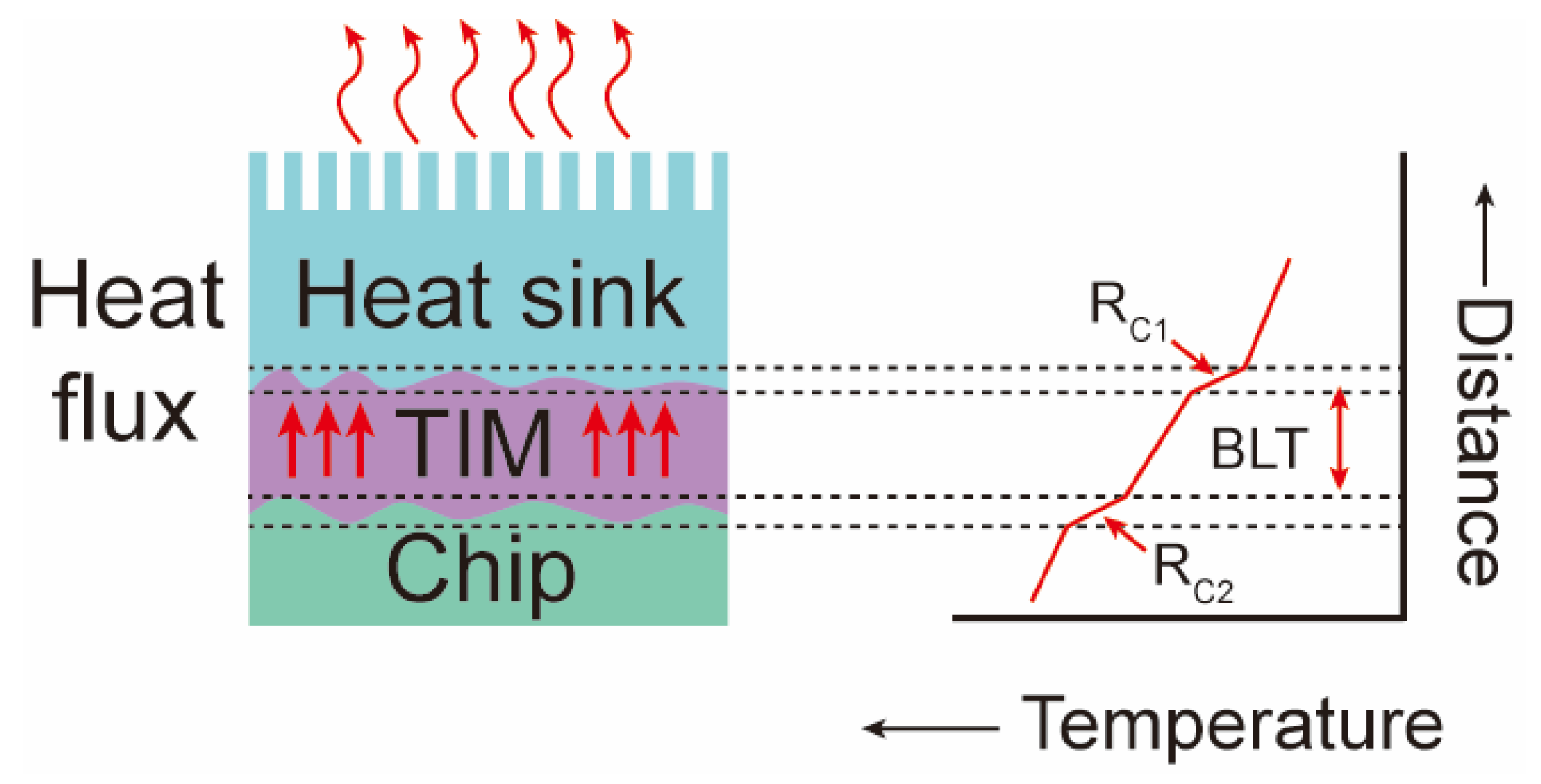
Figure 1. Schematic diagram of heat dissipation and interfacial thermal resistance in high-power electronics.
When calculating BLT, a suitable calculation model should be selected according to the physical state of TIMs. Prasher’s scaling-bulk model [24] showed BLT is primarily related with the yield stress of the polymer matrix τy. The formula can be given as [25]:
where r is the substrate radius, P is the applied pressure, c is a constant number, and d is the particle diameter. Hu [26] introduced a two-medium model of fluid viscidity and filler particle contact interactions, and found that BLT is highly related to the particle contact interactions when the thickness of the TIM decreases to a particular value.
The properties of the contact surface, such as the surface roughness, thermal conductivity of the contacting materials, hardness and contact pressure, can influence the thermal contact resistance [27]. The sum of the thermal contact resistance Rc can be defined as:
where σ1 and σ2 are the roughness of the contact interfaces of the heat sink and chip materials, and Anominal and Areal are the nominal and actual microscopic area of the two contact interfaces, respectively.
For solid-like TIMs, plastic deformation can be used to estimate the ratio of the nominal and actual microscopic area. Thus, the total thermal contact resistance Rc can be further defined as [28]:
where k1 and k2 are the thermal conductivity of the heat sink and chip materials, m is the effective absolute mean asperity slope, P is the contact pressure, and H is the surface microhardness. The increase in contact pressure makes the surfaces fit more tightly, increases the contact area and enhances the heat transfer at the surface.
For liquid-like TIMs, the models based on the plastic deformation mentioned above are not applicable since these TIMs have high fluidity and will adhere to the substrate with no plastic deformation. In this case, Anominal and Areal need to be calculated by the difference in surface energy resulting from different adhesions of fluidic TIMs to the substrate surface [27].
2.2. Thermal Conductivity Models
The main heat conduct carriers are electrons in the case of metals above room temperature, while the main carriers are phonons in the case of nonmetal. From a microscale point of view, the thermal resistance at the interfaces between the matrix and fillers inside the composite materials is attributed to the difference in electron or phonon vibration properties [23]. Electron and phonon scattering will occur while heat carriers are passing through the contact interface; therefore, the large difference in carrier density between two sides can cause a dramatically decrease in the thermal conductivity of composites, and thus impedes the heat transfer process.
Since most TIMs are composites, both phonons and electrons can be the carriers in conducting heat, and various models are used to calculate their thermal conductivities. For metals and alloys, the electronic transport efficiency is high and is involved in the conduction of thermal and electrical energy. The Wiedemann–Franz law [29] indicates that thermal conductivity is proportional to the electrical conductivity. The scattering and electron–electron interactions at the surface will also impact the thermal conductivity of metals and alloys.
In addition to metal-based TIMs, composite-based TIMs cover a wide range, and plenty of models can be used to calculate their thermal conductivity.
One of the typical composite-based TIMs is composed of an organic matrix and highly thermal conductive fillers. The Maxwell model [30][31] can characterize polymer-based composites with randomly dispersed sphere-shaped fillers at a low volume fraction, which does not include the interfacial thermal resistance between matrix and fillers. Based on the Maxwell model, the Hasselman and Johnson model [32] considers the influence of the filler size and interfacial thermal resistance between the filler and matrix to calculate the thermal conductivity. This model uses the reciprocal of the interfacial thermal conductance to represent interfacial thermal resistance and is widely used in predicting the thermal conductivity of metal-based and carbon-based composites. The phonon–electron interaction at the filler–matrix interfaces will increase the interfacial thermal resistance and make it nonnegligible. Molina et al. [33] employed the Hasselman–Johnson model to estimate the effect of porosity on the thermal conductivity of Al-12 wt % Si–graphite composites. Caccia and coworkers [34] improved the interfacial thermal conductance of Al–diamond composites via surface modification of diamond particles. They successfully utilized Maxwell and Hasselman–Johnson models to predict the thermal conductivity of the samples. In addition, Prieto and his coworkers [35] investigated the influence of the amount and particle size of SiC on graphite flakes–SiC particles–metal composites, whose theoretical thermal conductivity was predicted by the Hasselman–Johnson model. On the contrary, the Bruggeman model [36][37] uses mean field theory to consider the interactions between matrices and fillers. Furthermore, it can be also applied at relatively high volume fractions [38]. There are also more comprehensive models that consider the type, shape and size distribution of fillers and these models can all be applied in TIMs with nanoscale fillers according to the previous works [30][34][39][40][41].
As for the other inorganic TIMs composed of carbon or other cubic III–V compounds, phonon transport is the main heat conduction path. The slack model [42] can be used to explain the high thermal conductivity of graphite, diamond-like [43] and boron carbide crystal structures. For these inorganic TIMs, with a low atomic mass of constituent elements, high bonding strength, simple crystal structure and less phonon collision, the heat transfer will be largely enhanced.
One method used to improve thermal conductivity [44] includes increasing the number of fillers to induce thermal percolation [23], which can create a network in the material for thermal conduction and form effective heat transfer paths. Another effective way is to reduce interfacial thermal resistance by surface modification of fillers. The formation of an intermetallic alloy with high thermal conductivity can accelerate the heat transfer rate in metal-based TIMs. If fillers have thermal conducting anisotropy, uniform alignment will increase the thermal conductivity in a specific direction.
References
- Li, X.; Chen, X.; Lu, G.-Q. Reliability of High-Power Light Emitting Diode Attached with Different Thermal Interface Materials. J. Electron. Packag. 2010, 132, 031011.
- Jones, E.A.; de Rooij, M. High-Power-Density GaN-Based Converters: Thermal Management Considerations. IEEE Power Electron. Mag. 2019, 6, 22–29.
- Cui, Y.; Li, M.; Hu, Y. Emerging interface materials for electronics thermal management: Experiments, modeling, and new opportunities. J. Mater. Chem. C 2020, 8, 10568–10586.
- Deng, S.; Zhang, X.; Xiao, G.D.; Zhang, K.; He, X.; Xin, S.; Liu, X.; Zhong, A.; Chai, Y. Thermal interface material with graphene enhanced sintered copper for high temperature power electronics. Nanotechnology 2021, 32, 31011.
- McGlen, R.J.; Jachuck, R.; Lin, S. Integrated thermal management techniques for high power electronic devices. Appl. Therm. Eng. 2004, 24, 1143–1156.
- Otiaba, K.C.; Ekere, N.N.; Bhatti, R.S.; Mallik, S.; Alam, M.O.; Amalu, E.H. Thermal interface materials for automotive electronic control unit: Trends, technology and R&D challenges. Microelectron. Reliab. 2011, 51, 2031–2043.
- Suresh, R.; Bloschock, K.P.; Bar-Cohen, A. Advanced thermal management technologies for defense electronics. In Proceedings of the Defense Transformation and Net-Centric Systems 2012, Baltimore, MD, USA, 23–27 April 2012.
- Yoonjin, W.; Jungwan, C.; Agonafer, D.; Asheghi, M.; Goodson, K.E. Fundamental Cooling Limits for High Power Density Gallium Nitride Electronics. IEEE Trans. Compon. Packag. Manuf. Technol. 2015, 5, 737–744.
- Schulz, M.; Allen, S.T.; Pohl, W. The crucial influence of thermal interface material in power electronic design. In Proceedings of the IEEE Semiconductor Thermal Measurement & Management Symposium, San Jose, CA, USA, 17–21 March 2013.
- Qinglin, T.; Dongcheng, L.; Yanping, Z.; Xin, L.; Lihua, Z. Research on the uniform temperature of heat dissipation for the reverse oblique microchannel. In Proceedings of the 2021 22nd International Conference on Electronic Packaging Technology (ICEPT), Xiamen, China, 14–17 September 2021.
- Kang, T.; Ye, Y.X.; Jia, Y.C.; Kong, Y.M.; Jiao, B.B. Enhanced Thermal Management of GaN Power Amplifier Electronics with Micro-Pin Fin Heat Sinks. Electronics 2020, 9, 1778.
- Lumbreras, D.; Vilella, M.; Zaragoza, J.; Berbel, N.; Jorda, J.; Collado, A. Effect of the Heat Dissipation System on Hard-Switching GaN-Based Power Converters for Energy Conversion. Energies 2021, 14, 6287.
- Sarvar, F.; Whalley, D.; Conway, P. Thermal Interface Materials—A Review of the State of the Art. Electron. Syst. Technol. Conf. 2006, 2, 1292–1302.
- Zhou, J.; Li, B.-W. The physics of heat dissipation in micro-nano-scale devices. Wuli 2013, 42, 89–99.
- Chen, J.; Xu, X.; Zhou, J.; Li, B. Interfacial thermal resistance: Past, present, and future. Rev. Mod. Phys. 2022, 94, 025002.
- Zhang, P.; Yuan, P.; Jiang, X.; Zhai, S.P.; Zeng, J.H.; Xian, Y.Q.; Qin, H.B.; Yang, D.G. A Theoretical Review on Interfacial Thermal Transport at the Nanoscale. Small 2018, 14, 1702769.
- Swartz, E.T.; Pohl, R.O. Thermal boundary resistance. Rev. Mod. Phys. 1989, 61, 605–668.
- Prasher, R. Acoustic mismatch model for thermal contact resistance of van der Waals contacts. Appl. Phys. Lett. 2009, 94, 041905.
- Hopkins, P.E.; Norris, P.M. Effects of joint vibrational states on thermal boundary conductance. Nanoscale Microscale Thermophys. Eng. 2007, 11, 247–257.
- Belmabrouk, H.; Rezgui, H.; Nasri, F.; Aissa, M.F.B.; Guizani, A.A. Interfacial heat transport across multilayer nanofilms in ballistic–diffusive regime. Eur. Phys. J. Plus 2020, 135, 109.
- Stevens, R.J.; Zhigilei, L.V.; Norris, P.M. Effects of temperature and disorder on thermal boundary conductance at solid-solid interfaces: Nonequilibrium molecular dynamics simulations. Int. J. Heat Mass Transf. 2007, 50, 3977–3989.
- Dai, J.; Tian, Z. Rigorous formalism of anharmonic atomistic Green’s function for three-dimensional interfaces. Phys. Rev. B 2020, 101, 041301.
- Shahil, K.M.F.; Balandin, A.A. Graphene-Multilayer Graphene Nanocomposites as Highly Efficient Thermal Interface Materials. Nano Lett. 2012, 12, 861–867.
- Prasher, R.S.; Matayabas, J.C. Thermal contact resistance of cured gel polymeric thermal interface material. IEEE Trans. Compon. Packag. Technol. 2004, 24, 702–709.
- Prasher, R. Thermal interface materials: Historical perspective, status, and future directions. Proc. IEEE 2006, 94, 1571–1586.
- Hu, X.; Govindasamy, S.; Goodson, K.E. Two-Medium Model for the Bond Line Thickness of Particle Filled Thermal Interface Materials. In Proceedings of the ASME International Mechanical Engineering Congress & Exposition, Anaheim, CA, USA, 13–19 November 2004.
- Prasher, R.S. Surface chemistry and characteristics based model for the thermal contact resistance of fluidic interstitial thermal interface materials. J. Heat Transf.-Trans. Asme 2001, 123, 969–975.
- Wang, H.; Feng, J.Y.; Hu, X.J.; Ng, K.M. Reducing thermal contact resistance using a bilayer aligned CNT thermal interface material. Chem. Eng. Sci. 2010, 65, 1101–1108.
- Giordanengo, B.; Benazzi, N.; Vinckel, J.; Gasser, J.G.; Roubi, L. Thermal conductivity of liquid metals and metallic alloys. J. Non-Cryst. Solids 1999, 250, 377–383.
- Wang, J.; Li, J.J.; Weng, G.J.; Su, Y. The effects of temperature and alignment state of nanofillers on the thermal conductivity of both metal and nonmetal based graphene nanocomposites. Acta Mater. 2020, 185, 461–473.
- Xu, J.Z.; Gao, B.Z.; Kang, F.Y. A reconstruction of Maxwell model for effective thermal conductivity of composite materials. Appl. Therm. Eng. 2016, 102, 972–979.
- Hasselman, D.P.H.; Johnson, L.F. Effective Thermal Conductivity of Composites with Interfacial Thermal Barrier Resistance. J. Compos. Mater. 1989, 21, 508–515.
- Molina, J.M.; Rodriguez-Guerrero, A.; Louis, E.; Rodriguez-Reinoso, F.; Narciso, J. Porosity Effect on Thermal Properties of Al-12 wt % Si/Graphite Composites. Materials 2017, 10, 177.
- Caccia, M.; Rodriguez, A.; Narciso, J. Diamond Surface Modification to Enhance Interfacial Thermal Conductivity in Al/Diamond Composites. JOM 2014, 66, 920–925.
- Prieto, R.; Molina, J.M.; Narciso, J.; Louis, E. Thermal conductivity of graphite flakes-SiC particles/metal composites. Compos. Part A Appl. Sci. Manuf. 2011, 42, 1970–1977.
- Yang, X.T.; Liang, C.B.; Ma, T.B.; Guo, Y.Q.; Kong, J.; Gu, J.W.; Chen, M.J.; Zhu, J.H. A review on thermally conductive polymeric composites: Classification, measurement, model and equations, mechanism and fabrication methods. Adv. Compos. Hybrid Mater. 2018, 1, 207–230.
- Pietrak, K.; Wiśniewski, T.S. A review of models for effective thermal conductivity of composite materials. J. Power Technol. 2014, 95, 14–24.
- Li, H.K.; Zheng, W.D. Enhanced thermal conductivity of epoxy/alumina composite through multiscale-disperse packing. J. Compos. Mater. 2021, 55, 17–25.
- Jung, J.; Jeong, S.H.; Hjort, K.; Ryu, S. Investigation of thermal conductivity for liquid metal composites using the micromechanics-based mean-field homogenization theory. Soft Matter 2020, 16, 5840–5847.
- Kochetov, R.; Korobko, A.V.; Andritsch, T.; Morshuis, P.H.F.; Picken, S.J.; Smit, J.J. Modelling of the thermal conductivity in polymer nanocomposites and the impact of the interface between filler and matrix. J. Phys. D Appl. Phys. 2011, 44, 395401.
- Liang, L.H.; Wei, Y.G.; Li, B. Thermal conductivity of composites with nanoscale inclusions and size-dependent percolation. J. Phys. Condens. Matter 2008, 20, 365201.
- Slack, G.A. Nonmetallic crystals with high thermal conductivity. J. Phys. Chem. Solids 1973, 34, 321–335.
- Ziambaras, E.; Hyldgaard, P. Thermal transport in SiC nanostructures. Mater. Sci. Eng. C Biomim. Supramol. Syst. 2005, 25, 635–640.
- Mehra, N.; Mu, L.W.; Ji, T.; Yang, X.T.; Kong, J.; Gu, J.W.; Zhu, J.H. Thermal transport in polymeric materials and across composite interfaces. Appl. Mater. Today 2018, 12, 92–130.
More
Information
Subjects:
Materials Science, Composites
Contributors
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
2.6K
Revisions:
3 times
(View History)
Update Date:
31 Oct 2022
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




