1. Algebraic Methods

Nozzle Geometry

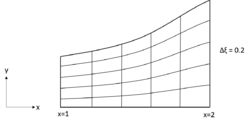
The grid generation by algebraic methods is based on mathematical interpolation function. It is done by using known functions in one, two or three dimensions taking arbitrary shaped regions. The computational domain might not be rectangular, but for the sake of simplicity, the domain is taken to be rectangular. The main advantage of the methods is that they provide explicit control of physical grid shape and spacing. The simplest procedure that may be used to produce boundary fitted computational mesh is the normalization transformation.^[1]
For a nozzle, with the describing function [math]\displaystyle{ y = x^2 }[/math] the grid can easily be generated using uniform division in y-direction with equally spaced increments in x-direction, which are described by

[math]\displaystyle{ \xi=x \, }[/math]

[math]\displaystyle{ \eta = \frac{y}{y_\max} \, }[/math]

where [math]\displaystyle{ y_\max }[/math] denotes the y-coordinate of the nozzle wall. For given values of ([math]\displaystyle{ \xi }[/math], [math]\displaystyle{ \eta }[/math]), the values of ([math]\displaystyle{ x }[/math], [math]\displaystyle{ y }[/math]) can be easily recovered.

2. Differential Equation Methods

Like algebraic methods, differential equation methods are also used to generate grids. The advantage of using the partial differential equations (PDEs) is that the solution of grid generating equations can be exploited to generate the mesh. Grid construction can be done using all three classes of partial differential equations.

2.1. Elliptic Schemes

Elliptic PDEs generally have very smooth solutions leading to smooth contours. Using its smoothness as an advantage Laplace's equations can preferably be used because the Jacobian found out to be positive as a result of maximum principle for harmonic functions. After extensive work done by Crowley (1962) and Winslow (1966)^[2] on PDEs by transforming physical domain into computational plane while mapping using Poisson’s equation, Thompson et al. (1974)^[3] have worked extensively on elliptic PDEs to generate grids. In Poisson grid generators, the mapping is accomplished by marking the desired grid points [math]\displaystyle{ (x,y) }[/math] on the boundary of the physical domain, with the interior point distribution determined through the solution of equations written below

[math]\displaystyle{ \xi_{xx} + \xi_{yy} = P(\xi, \eta) }[/math]

[math]\displaystyle{ \eta_{xx} + \eta_{yy} = Q(\xi, \eta) }[/math]

where, [math]\displaystyle{ (\xi,\eta) }[/math] are the co-ordinates in the computational domain, while P and Q are responsible for point spacing within D. Transforming above equations in computational space yields a set of two elliptic PDEs of the form,

[math]\displaystyle{ \alpha x_{\xi\xi} -2\beta x_{\xi\eta} + \gamma x_{\eta\eta} = -I^2 (Px_\xi + Qx_\eta) }[/math]

[math]\displaystyle{ \alpha y_{\xi\xi} -2\beta y_{\xi\eta} + \gamma y_{\eta\eta} = -I^2 (Py_\xi + Qy_\eta) }[/math]

where

[math]\displaystyle{ \begin{align} \alpha & = x^2_\eta + y^2_\eta \\ \beta & = x_\eta x_\xi + y_\xi y_\eta \\ \gamma & = x^2_\xi + y^2_\xi \\ I & = \frac{\delta(x, y)}{\delta(\xi, \eta)} = y_\eta x_\xi - y_\xi x_\eta \end{align} }[/math]

These systems of equations are solved in the computational plane on uniformly spaced grid which provides us with the [math]\displaystyle{ (x,y) }[/math] co-ordinates of each point in physical space. The advantage of using elliptic PDEs is the solution linked to them is smooth and the resulting grid is smooth. But, specification of P and Q becomes a difficult task thus adding it to its disadvantages. Moreover, the grid has to be computed after each time step which adds up to computational time.^[4]

2.2. Hyperbolic Schemes

This grid generation scheme is generally applicable to problems with open domains consistent with the type of PDE describing the physical problem. The advantage associated with hyperbolic PDEs is that the governing equations need to be solved only once for generating grid. The initial point distribution along with the approximate boundary conditions forms the required input and the solution is the then marched outward. Steger and Sorenson (1980)^[5] proposed a volume orthogonality method that uses Hyperbolic PDEs for mesh generation. For a 2-D problem, Considering computational space to be given by [math]\displaystyle{ \Delta\xi = \Delta\eta = 1 }[/math], the inverse of the Jacobian is given by,

[math]\displaystyle{ x_\xi y_\eta - x_\eta y_\xi = I }[/math]

where [math]\displaystyle{ I }[/math] represents the area in physical space for a given area in computational space. The second equation links the orthogonality of grid lines at the boundary in physical space which can be written as

[math]\displaystyle{ d\xi = 0 = \xi_x \, dx + \xi_y \, dy. }[/math]

For [math]\displaystyle{ \xi }[/math] and [math]\displaystyle{ \eta }[/math] surfaces to be perpendicular the equation becomes

[math]\displaystyle{ x_\xi x_\eta + y_\xi y_\eta = 0. }[/math]

The problem associated with such system of equations is the specification of [math]\displaystyle{ I }[/math]. Poor selection of [math]\displaystyle{ I }[/math] may lead to shock and discontinuous propagation of this information throughout the mesh. While mesh being orthogonal is generated very rapidly which comes out as an advantage with this method.

2.3. Parabolic Schemes

The solving technique is similar to that of hyperbolic PDEs by advancing the solution away from the initial data surface satisfying the boundary conditions at the end. Nakamura (1982) and Edwards (1985) developed the basic ideas for parabolic grid generation. The idea uses either of Laplace or the Poisson's equation and especially treating the parts which controls elliptic behavior. The initial values are given as the coordinates of the point along the surface [math]\displaystyle{ \eta = 0 }[/math] and the advancing the solutions to the outer surface of the object satisfying the boundary conditions along [math]\displaystyle{ \xi }[/math] edges.

The control of the grid spacing has not been suggested till now. Nakamura and Edwards, grid control was accomplished using non uniform spacing. The parabolic grid generation shows an advantage over the hyperbolic grid generation that, no shocks or discontinuities occur and the grid is relatively smooth. The specifications of initial values and selection of step size to control the grid points is however time consuming, but these techniques can be effective when familiarity and experience is gained.

3. Variational Methods

This method includes a technique that minimizes grid smoothness, orthogonality and volume variation. This method forms mathematical platform to solve grid generation problems. In this method an alternative grid is generated by a new mesh after each iteration and computing the grid speed using backward difference method. This technique is a powerful one with a disadvantage that effort is required to solve the equations related to grid. Further work needed to be done to minimize the integrals that will reduce the CPU time.

4. Unstructured Grid Generation

See also Mesh generation. The main importance of this scheme is that it provides a method that will generate the grid automatically. Using this method, grids are segmented into blocks according to the surface of the element and a structure is provided to ensure appropriate connectivity. To interpret the data flow solver is used. When an unstructured scheme is employed, the main interest is to fulfill the demand of the user and a grid generator is used to accomplish this task. The information storage in structured scheme is cell to cell instead of grid to grid and hence the more memory space is needed. Due to random cell location, the solver efficiency in unstructured is less as compared to the structured scheme.^[6]

Some points are needed to be kept in mind at the time of grid construction. The grid point with high resolution creates difficulty for both structured and unstructured. For example, in case of boundary layer, structured scheme produces elongated grid in the direction of flow. On the other hand unstructured grids require a higher cell density in the boundary layer because the cell needs to be as equilateral as possible to avoid errors.^[7]

4.1. Connectivity Information

We must identify what information is required to identify the cell and all the neighbors of the cell in the computational mesh. We can choose to locate the arbitrary points anywhere we want for the unstructured grid. A point insertion scheme is used to insert the points independently and the cell connectivity is determined. This suggests that the point be identified as they are inserted. Logic for establishing new connectivity is determined once the points are inserted. Data that form grid point that identifies grid cell are needed. As each cell is formed it is numbered and the points are sorted. In addition the neighbor cell information is needed.

5. Adaptive Grid

A problem in solving partial differential equations using previous methods is that the grid is constructed and the points are distributed in the physical domain before details of the solution is known. So the grid may or may not be the best for the given problem.^[8]

Adaptive methods are used to improve the accuracy of the solutions. The adaptive method is referred to as ‘h’ method if mesh refinement is used, ‘r’ method if the number of grid point is fixed and not redistributed and ‘p’ if the order of solution scheme is increased in finite-element theory. The multi dimensional problems using the equidistribution scheme can be accomplished in several ways. The simplest to understand are the Poisson Grid Generators with control function based on the equidistribution of the weight function with the diffusion set as a multiple of desired cell volume. The equidistribution scheme can also be applied to the unstructured problem. The problem is the connectivity hampers if mesh point movement is very large.

Steady flow and the time-accurate flow calculation can be solved through this adaptive method. The grid is refined and after a predetermined number of iteration in order to adapt it in a steady flow problem. The grid will stop adjusting to the changes once the solution converges. In time accurate case coupling of the partial differential equations of the physical problem and those describing the grid movement is required.