1. Volatility Terminology

Volatility as described here refers to the actual volatility, more specifically:

• actual current volatility of a financial instrument for a specified period (for example 30 days or 90 days), based on historical prices over the specified period with the last observation the most recent price.
• actual historical volatility which refers to the volatility of a financial instrument over a specified period but with the last observation on a date in the past
  • near synonymous is realized volatility, the square root of the realized variance, in turn calculated using the sum of squared returns divided by the number of observations.
• actual future volatility which refers to the volatility of a financial instrument over a specified period starting at the current time and ending at a future date (normally the expiry date of an option)

Now turning to implied volatility, we have:

• historical implied volatility which refers to the implied volatility observed from historical prices of the financial instrument (normally options)
• current implied volatility which refers to the implied volatility observed from current prices of the financial instrument
• future implied volatility which refers to the implied volatility observed from future prices of the financial instrument

For a financial instrument whose price follows a Gaussian random walk, or Wiener process, the width of the distribution increases as time increases. This is because there is an increasing probability that the instrument's price will be farther away from the initial price as time increases. However, rather than increase linearly, the volatility increases with the square-root of time as time increases, because some fluctuations are expected to cancel each other out, so the most likely deviation after twice the time will not be twice the distance from zero.

Since observed price changes do not follow Gaussian distributions, others such as the Lévy distribution are often used.^[1] These can capture attributes such as "fat tails". Volatility is a statistical measure of dispersion around the average of any random variable such as market parameters etc.

2. Mathematical Definition

For any fund that evolves randomly with time, volatility is defined as the standard deviation of a sequence of random variables, each of which is the return of the fund over some corresponding sequence of (equally sized) times.

Thus, "annualized" volatility σ_annually is the standard deviation of an instrument's yearly logarithmic returns.^[2]

The generalized volatility σ_T for time horizon T in years is expressed as:

[math]\displaystyle{ \sigma_\text{T} = \sigma_\text{annually} \sqrt{T}. }[/math]

Therefore, if the daily logarithmic returns of a stock have a standard deviation of σ_daily and the time period of returns is P in trading days, the annualized volatility is

[math]\displaystyle{ \sigma_\text{P} = \sigma_\text{daily} \sqrt{P}. }[/math]

A common assumption is that P = 252 trading days in any given year. Then, if σ_daily = 0.01, the annualized volatility is

[math]\displaystyle{ \sigma_\text{annually} = 0.01 \sqrt{252} = 0.1587. }[/math]

The monthly volatility (i.e., T = 1/12 of a year or P = 252/12 = 21 trading days) would be

[math]\displaystyle{ \sigma_\text{monthly} = 0.1587 \sqrt{\tfrac{1}{12}} = 0.0458. }[/math]

[math]\displaystyle{ \sigma_\text{monthly} = 0.01 \sqrt{\tfrac{252}{12}} = 0.0458. }[/math]

The formulas used above to convert returns or volatility measures from one time period to another assume a particular underlying model or process. These formulas are accurate extrapolations of a random walk, or Wiener process, whose steps have finite variance. However, more generally, for natural stochastic processes, the precise relationship between volatility measures for different time periods is more complicated. Some use the Lévy stability exponent α to extrapolate natural processes:

[math]\displaystyle{ \sigma_T = T^{1/\alpha} \sigma.\, }[/math]

If α = 2 the Wiener process scaling relation is obtained, but some people believe α < 2 for financial activities such as stocks, indexes and so on. This was discovered by Benoît Mandelbrot, who looked at cotton prices and found that they followed a Lévy alpha-stable distribution with α = 1.7. (See New Scientist, 19 April 1997.)

3. Volatility Origin

Much research has been devoted to modeling and forecasting the volatility of financial returns, and yet few theoretical models explain how volatility comes to exist in the first place.

Roll (1984) shows that volatility is affected by market microstructure.^[3] Glosten and Milgrom (1985) shows that at least one source of volatility can be explained by the liquidity provision process. When market makers infer the possibility of adverse selection, they adjust their trading ranges, which in turn increases the band of price oscillation.^[4]

In September 2019, JPMorgan Chase determined the effect of US President Donald Trump's tweets, and called it the Volfefe index combining volatility and the covfefe meme.

4. Volatility for Investors

Investors care about volatility for at least eight reasons:

1. The wider the swings in an investment's price, the harder emotionally it is to not worry;
2. Price volatility of a trading instrument can define position sizing in a portfolio;
3. When certain cash flows from selling a security are needed at a specific future date, higher volatility means a greater chance of a shortfall;
4. Higher volatility of returns while saving for retirement results in a wider distribution of possible final portfolio values;
5. Higher volatility of return when retired gives withdrawals a larger permanent impact on the portfolio's value;
6. Price volatility presents opportunities to buy assets cheaply and sell when overpriced;
7. Portfolio volatility has a negative impact on the compound annual growth rate (CAGR) of that portfolio
8. Volatility affects pricing of options, being a parameter of the Black–Scholes model.

In today's markets, it is also possible to trade volatility directly, through the use of derivative securities such as options and variance swaps. See Volatility arbitrage.

5. Volatility Versus Direction

Volatility does not measure the direction of price changes, merely their dispersion. This is because when calculating standard deviation (or variance), all differences are squared, so that negative and positive differences are combined into one quantity. Two instruments with different volatilities may have the same expected return, but the instrument with higher volatility will have larger swings in values over a given period of time.

For example, a lower volatility stock may have an expected (average) return of 7%, with annual volatility of 5%. This would indicate returns from approximately negative 3% to positive 17% most of the time (19 times out of 20, or 95% via a two standard deviation rule). A higher volatility stock, with the same expected return of 7% but with annual volatility of 20%, would indicate returns from approximately negative 33% to positive 47% most of the time (19 times out of 20, or 95%). These estimates assume a normal distribution; in reality stocks are found to be leptokurtotic.

6. Volatility over Time

Although the Black-Scholes equation assumes predictable constant volatility, this is not observed in real markets, and amongst the models are Emanuel Derman and Iraj Kani's^[5] and Bruno Dupire's local volatility, Poisson process where volatility jumps to new levels with a predictable frequency, and the increasingly popular Heston model of stochastic volatility.^[6][link broken]

It is common knowledge that types of assets experience periods of high and low volatility. That is, during some periods, prices go up and down quickly, while during other times they barely move at all.^[7] In foreign exchange market, price changes are seasonally heteroskedastic with periods of one day and one week.^[8][9]

Periods when prices fall quickly (a crash) are often followed by prices going down even more, or going up by an unusual amount. Also, a time when prices rise quickly (a possible bubble) may often be followed by prices going up even more, or going down by an unusual amount.

Most typically, extreme movements do not appear 'out of nowhere'; they are presaged by larger movements than usual. This is termed autoregressive conditional heteroskedasticity. Whether such large movements have the same direction, or the opposite, is more difficult to say. And an increase in volatility does not always presage a further increase—the volatility may simply go back down again.

Not only the volatility depends on the period when it is measured but also on the selected time resolution. The effect is observed due to the fact that the information flow between short-term and long-term traders is asymmetric. As a result, volatility measured with high resolution contains information that is not covered by low resolution volatility and vice versa.^[10]

The risk parity weighted volatility of the three assets Gold, Treasury bonds and Nasdaq acting as proxy for the Marketportfolio seems to have a low point at 4% after turning upwards for the 8th time since 1974 at this reading in the summer of 2014.

7. Alternative Measures of Volatility

Some authors point out that realized volatility and implied volatility are backward and forward looking measures, and do not reflect current volatility. To address that issue an alternative, ensemble measures of volatility were suggested. Introduction The ability of investors to trade any amount of a security without affecting its price is critical to proving a number of important theorems. However, there are several market frictions that influence price formation. These frictions include, among other things, trading fees, short-sale restrictions, and circuit breakers. For a long time, it has been recognized that market flaws influence asset pricing. Traders, regulators, exchange officials, and academics have all placed a high priority on liquidity. The purpose of this article is to assist readers in understanding the theories that guide investors through the process of trading stocks without affecting the price. Liquidity can be described as the capability of promptly purchasing or selling large quantities of an object at a price that is acceptable to the seller. The great majority of models that estimate the equilibrium value of assets omit trading. These models also disregard the amount of time and effort that is necessary to transform cash into financial assets or vice versa. On the other hand, recent economic and financial crises have shown that market circumstances can be fairly severe at times, with liquidity evaporating on occasion. This is one of the lessons that can be learned from these events. This is one of the ways in which the availability of liquidity can have an effect on the value of assets. The works of Amihud and Mendelson (1986) and Jacoby, Fowler, and Gottesman provide theoretical explanations for the impact that liquidity has on the values of assets traded on financial markets (2000). Jones (2001) and Amihud (2002) show that liquidity can accurately forecast predicted returns in time series data. Both of these studies were conducted in 2001 and 2002. According to Pastor and Stambaugh's research from 2001, a cross-sectional relationship exists between predicted stock returns and liquidity risk. Up to this point, the stock market and the bond market have each been the subject of separate research. The evidence suggests that the stock market and bond markets have distinct levels of liquidity. Strong volatility links between the two markets (Fleming, Kirby, and Ostdiek, 1998), despite the low unconditional correlation between stock and bond returns (Campbell and Ammer, 1993), can affect liquidity in both markets by changing the inventory risk taken on by market-making agents (Ho and Stoll, 1983; O'Hara and Old eld, 1986). Low unconditional correlation between stock and bond returns, according to Campbell and Ammer (1993), was linked to high volatility between the two markets. The returns on equities and bonds did not correlate, although Campbell and Ammer (1993) found that there was substantial volatility. Market liquidity for bonds and stocks can be impacted by trading activity. Asset allocation strategies will really rebalance wealth between the bond and equity markets. 4 A negative information shock in the stock market is typically followed by a "right to quality," in which investors seek assets with lower levels of risk. This can lead to a rise in stock prices and affect the bond and stock markets' liquidity. The information presented suggests that liquidity may exhibit inertia across asset classes and may be impacted by systemic shocks to volatility, returns, and trading activity. The discussion demonstrates that asset class liquidity might stay flat. Trading data From June 17, 1991 to December 31, 1998, bond and equity liquidity data were gathered. The sample period doesn't include GovPX Inc.'s tick-by-tick Treasury bond data. This data shows major dealers' interdealer broker market transactions. ISSM and TAQ give stock statistics (trades and automated quotations). ISSM data include 1991-1992, TAQ data 1993-1998. We exclusively utilize NYSE-listed stocks, so we don't have to worry about other trading methods skewing the results. This research examines the factors that affect quoted spreads and market depth, which are used to measure the liquidity of stocks and bonds. Previous study suggests that returns, volatility, and trade activity explain this behavior (such as that done by Amihud and Mendelson in 1986, Benston and Hagerman in 1974, and Hasbrouck in 1991). Order imbalances have a higher relationship to trading costs than volume because they put pressure on market makers' inventory. Volume is the number of transactions in a given time period. Using transaction data, we derive liquidity measures. In the next paragraph, we explore imbalance measurements obtained from transaction databases. Liquidity imbalance indicators GovPX, Inc. gathers data from primary brokers in order to provide real-time data to online retailers. GovPX provides real-time data to these online stores. This service not only provides information on the price and quantity, both of which are expressed in millions of dollars, but it also provides information on who initiated each deal and who made the highest bid. Every transaction begins and ends at a specific time. For the time being, GovPX can only record and monitor transactions between dealers. We use on-the-run 10-year Treasury notes to capitalize on the liquidity that exists in the markets for long-term fixed income investments. Even though on-the-run assets account for 71% of all interdealer transactions, Treasury securities account for a relatively minor portion of these totals (Fabozzi and Fleming, 2000). We have decided not to analyze the 30-year Treasury bond because GovPX data only captures a small and constantly changing percentage of total market activity, and because a prominent broker, Cantor Fitzgerald/eSpeed, does not share its data. This decision was made because GovPX data only captures a small portion of total market activity. We have concluded that we cannot proceed with the analysis due to the presence of these variables. Liquidity imbalance Based on the following criteria, stocks may be included or omitted within a calendar year. 1. A stock must be listed in CRSP and intraday databases at the beginning and end of the year. 2. Companies that transferred from Nasdaq to NYSE during the year were eliminated from the sample (during the time span of our sample, no companies moved from the NYSE to the Nasdaq). 3. Certificates, ADRs, shares of beneficial interest, units, foreign corporations, Americus Trust components, closed-end funds, preferred stocks, and REITs were omitted from the portfolio since their trading characteristics differ from conventional equities. 4. To avoid inaccurate results from excessively high stock prices, the company's shares were eliminated from the study if the price at the end of any month was more than $999. Intraday data was purged because of trades recorded before or after the open, unexpected settlement circumstances, and out-of-order trades (because they might be subject to distinct liquidity considerations) We'll research market liquidity for stocks and bonds. Table 1 displays differences and imbalances. Specifically, we are discussing the prices of bonds and shares. We examined bid-ask spreads before and after the reduction in US tick sizes on June 24, 1997. (see, Chordia, Roll, and Subrahmanyam, 2001). little parasites, like ticks. Bond spreads typically range between $0.032 and $0.20, whereas stock spreads are in between. The median spread readings being close to averages is evidence that the daily liquidity skewness is minimal. The daily absolute difference between stocks and bonds is 5%, while the daily difference between bonds and stocks is 13%. The tick size adjustment has caused stock spreads to contract, validating earlier studies. The stock market's order imbalance is reducing. Tick size modifications have little impact on bond spreads or order imbalances. Bond spreads have remained constant despite an increase in trading volume and order mismatches. 12 Bond ticks may get smaller in size in the future. Why bond spreads are decreasing Treasury bond prices are impacted by monetary policy, unemployment, and inflation. Adverse selection doesn't worry bond markets. Vector autoregression We study the intertemporal links between market liquidity, returns, volatility, and order imbalances. Previous study has partially addressed univariate relationships between liquidity and the latter three variables, but there is still reason to believe they have a bidirectional causal relationship. Amihud and Mendelson hypothesized that liquidity can effect returns by paying a premium for trading fees (1986). Returns may affect future trading behavior and liquidity. Loss aversion, for example, implies return-dependent investing behavior (Odean, 1998), and a price-change-caused wave of trade might strain liquidity. Both might affect the market. Benston and Hagerman (1974) then examine volatility and liquidity. Rising volatility increases inventory risk and bid-ask spread, say the authors. Reduced liquidity might cause asset price volatility (see, e.g., Subrahmanyam, 1994). Chordia, Roll, and Subrahmanyam explore imbalances and liquidity (2002). Days with a significant negative imbalance and return are followed by days with a return reversal, ostensibly due to strained market maker inventories or investor overreaction and correction. Order imbalances could happen if increasing liquidity makes assets more desirable and encourages agents to buy them. There is a risk that there will be significant cross-market implications between the bond and equity markets. Trading activity and liquidity in one market may be able to forecast trading activity and liquidity in another market if there are leads and lags associated with asset allocation agreements between markets. Cross-effects can be produced by the lags and leads of volatility and liquidity shocks. The future liquidity of one market may be impacted by the market's rejection of systemic (macro) shocks to its volatility and liquidity. The arguments previously mentioned apply to the consequences of cross-market interactions to the extent that the variables of one market can anticipate those of another market. Estimations First, determine if the sum of each regressor's coefficients deviates sufficiently from zero. Second, determine if a regressor Granger-causes the dependent variable. In Panel A of Table 4, the total coefficients for each VAR regressor are given together with Granger causality test p-values. First, we'll examine how quoted spreads affect endogenous variables. Spread lags are key. In both markets, spreads and volatility are causally related. Cross-market causalities stand out. Stock and bond spreads at 10% are causally related. Stock returns and volatility directly affect bond spreads but indirectly affect stock spreads. Granger's impact causes bond returns to affect stock volatility. Conclusion From 1991 to 1998, we look at how the flow of money (bank reserves and mutual fund investments) affected the liquidity of transactions. By looking at how liquidity moves together across different types of assets, our research helps us learn more about how liquidity works. We also combine liquidity at the microstructure level with liquidity at the macro level, which is shown by money flows, to learn more about the forces that drive liquidity across markets. Our research is essential because of the link between liquidity and capital costs (Pastor and Stambaugh, 2001). It affects estimating and managing asset allocation trading expenses. Our biggest discoveries are: Stock and bond markets have similar weekly liquidities. Tuesdays and Fridays have the most and least market liquidity. In July through September, stock and bond market liquidity is stronger than in October. Shocks to volatility or spreads in one market affect spreads in the other over daily, biweekly, and monthly time frames. Volatility affects both stock and bond markets. Stock and bond markets have a positive correlation between unexpected liquidity shocks, as well as unexpected volatility shocks. The stock market may benefit from monetary policy relaxation, as demonstrated by a decrease in net borrowing reserves. Liquidity may benefit or suffer if the Federal Funds rate suddenly decreases (increases). Stocks and bonds are more volatile when the Federal Funds Rate changes (or reduce, depending on the direction). Our findings point to a possible investigation. Theoretical work on time-series liquidity shifts is scant, and there is no theory that combines the equity and fixed-income markets in any meaningful way. Neither of these topics has been adequately studied. Endogenous stock and bond trading in a market equilibrium model would be ideal. As monetary policy, money flows and stock and bond markets' liquidity are also unknown. Research in these areas should benefit from our efforts.

One of the measures is defined as the standard deviation of ensemble returns instead of time series of returns.^[11] Another considers the regular sequence of directional-changes as the proxy for the instantaneous volatility.^[12]

8. Implied Volatility Parametrisation

There exist several known parametrisations of the implied volatility surface, Schonbucher, SVI and gSVI.^[13]

9. Crude Volatility Estimation

Using a simplification of the above formula it is possible to estimate annualized volatility based solely on approximate observations. Suppose you notice that a market price index, which has a current value near 10,000, has moved about 100 points a day, on average, for many days. This would constitute a 1% daily movement, up or down.

To annualize this, you can use the "rule of 16", that is, multiply by 16 to get 16% as the annual volatility. The rationale for this is that 16 is the square root of 256, which is approximately the number of trading days in a year (252). This also uses the fact that the standard deviation of the sum of n independent variables (with equal standard deviations) is √n times the standard deviation of the individual variables.

The average magnitude of the observations is merely an approximation of the standard deviation of the market index. Assuming that the market index daily changes are normally distributed with mean zero and standard deviation σ, the expected value of the magnitude of the observations is √(2/π)σ = 0.798σ. The net effect is that this crude approach underestimates the true volatility by about 20%.

10. Estimate of Compound Annual Growth Rate (CAGR)

Consider the Taylor series:

[math]\displaystyle{ \log(1+y) = y - \tfrac{1}{2}y^2 + \tfrac{1}{3}y^3 - \tfrac{1}{4}y^4 + \cdots }[/math]

Taking only the first two terms one has:

[math]\displaystyle{ \mathrm{CAGR} \approx \mathrm{AR} - \tfrac{1}{2}\sigma^2 }[/math]

Volatility thus mathematically represents a drag on the CAGR (formalized as the "volatility tax"). Realistically, most financial assets have negative skewness and leptokurtosis, so this formula tends to be over-optimistic. Some people use the formula:

[math]\displaystyle{ \mathrm{CAGR} \approx \mathrm{AR} - \tfrac{1}{2}k\sigma^2 }[/math]

for a rough estimate, where k is an empirical factor (typically five to ten).

11. Criticisms of Volatility Forecasting Models

Performance of VIX (left) compared to past volatility (right) as 30-day volatility predictors, for the period of Jan 1990-Sep 2009. Volatility is measured as the standard deviation of S&P500 one-day returns over a month's period. The blue lines indicate linear regressions, resulting in the correlation coefficients r shown. Note that VIX has virtually the same predictive power as past volatility, insofar as the shown correlation coefficients are nearly identical. https://handwiki.org/wiki/index.php?curid=1238616

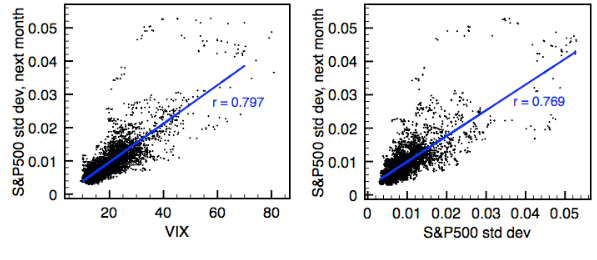
Despite the sophisticated composition of most volatility forecasting models, critics claim that their predictive power is similar to that of plain-vanilla measures, such as simple past volatility^[14][15] especially out-of-sample, where different data are used to estimate the models and to test them.^[16] Other works have agreed, but claim critics failed to correctly implement the more complicated models.^[17] Some practitioners and portfolio managers seem to completely ignore or dismiss volatility forecasting models. For example, Nassim Taleb famously titled one of his Journal of Portfolio Management papers "We Don't Quite Know What We are Talking About When We Talk About Volatility".^[18] In a similar note, Emanuel Derman expressed his disillusion with the enormous supply of empirical models unsupported by theory.^[19] He argues that, while "theories are attempts to uncover the hidden principles underpinning the world around us, as Albert Einstein did with his theory of relativity", we should remember that "models are metaphors – analogies that describe one thing relative to another".