1. Stellar Aberration Is Only Due to the Change of the Astronomer's Inertial Frame of Reference

In the year 1926 the astrophysicist Robert Emden published the article Aberration und Relativitätstheorie in the journal Naturwissenschaften.^[1] In this article he states that the direction of a light ray isn't influenced by the motion of the star or by the motion of Earth.^[2] At that time, the opponents of the special theory of relativity reasoned that the theory must be flawed, because it would state that the stellar aberration would depend on the relative velocity of the star — which would be in contradiction to observation — and R. Emden's article explains that the special theory of relativity does not predict this. Today, the special theory of relativity isn't contested anymore but there are still articles that suggest that the aberration would depend on the relative velocity of the star.^[3]

Although a (relativistic) velocity-addition formula can be used to explain stellar aberration, (see Aberration of light), another (relativistic) explanation using only the Lorentz transformation is also possible, as will be demonstrated. This derivation only uses the star's coordinates at the time of emission, and therefore has the formal advantage there is no place for the relative velocity of the star towards the astronomer and therefore it is evident that the observed position doesn't depend on the star's velocity — provided that the resultant change of position is much smaller than the distance between star and Earth.^[4] The observed position of the star wouldn't depend on Earth's motion either, if the astronomer could use the same inertial frame of reference all the time. But of course that is technically impossible,^[5] the astronomer uses his current rest frame and these current rest frames are different at different times as Earth orbits around the Sun. It is mathematically convenient to declare the position of the source star in the rest frame of the Sun (more exactly: the center of mass of the Solar System) as the "real" position and that the difference to this "real" position derives form the "aberration".^[6]

1.1. Sample Calculation

path of light signal in reference frame S. https://handwiki.org/wiki/index.php?curid=1292674

path of light signal in reference frame S'. https://handwiki.org/wiki/index.php?curid=1707113

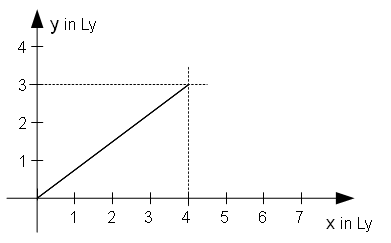
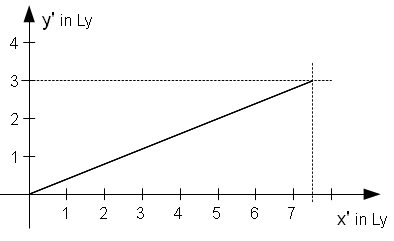
S and S' are (quasi-)inertial frames of reference and the reference frame S' is in uniform motion with v_x = 0.5c relative to S, such that in the future the star comes nearer to the origin of the coordinate system (and consequently further afar in the past). The x-,y- and z-axes of both systems ought to be parallel and at time t=t'=0 the origins of both systems ought to coincide. Therefore one gets according to Lorentz transformation: [math]\displaystyle{ \scriptstyle \beta=v/c }[/math], [math]\displaystyle{ \scriptstyle \gamma=1/\sqrt{1-\beta^{2}} }[/math]: y'=y ; z=z'; [math]\displaystyle{ \scriptstyle x'=\gamma\cdot(x-\beta\cdot ct) }[/math]

Suppose now that the star emitted a light signal at time [math]\displaystyle{ \scriptstyle c\,t_1=-5\,Ly }[/math] at location [math]\displaystyle{ \scriptstyle x_1=4\,Ly\;,\;y_1= 3\,Ly\;,\;z_1=0 }[/math] (S coordinates) and that this light signal is received by an astronomer at time [math]\displaystyle{ \scriptstyle c\,t_2=0 }[/math] at location [math]\displaystyle{ \scriptstyle x_2=0\;,\;y_2=0\;,\;z_2=0 }[/math].

In S the star's position and the x-axis form an angle [math]\displaystyle{ \delta }[/math] with [math]\displaystyle{ \scriptstyle \tan \delta =3/4 \; \rightarrow \;\delta =36.87^\circ }[/math] But in S' [math]\displaystyle{ \scriptstyle x_1'=\gamma \cdot (x_1-\beta \cdot c\,t_1)=1,1547\cdot (4 Lj - 0,5\cdot(-5 Lj))=7,50555 Lj; \quad y_1'=y_1=3 Lj }[/math] and therefore the angle [math]\displaystyle{ \delta' }[/math] between the star's position and x'-axis^[7] is [math]\displaystyle{ \scriptstyle \tan \delta'=y_1'/x_1'=3/7,50555\;\rightarrow\;\delta' = 21,79^\circ }[/math]

Calculation with help of the formula in aberration of light#Explanation gives the same result: [math]\displaystyle{ \scriptstyle \tan (\delta'/2) = \tan (\delta /2) \cdot \sqrt {(1-0,5)/(1+0,5)} = \tan (36,87^\circ/2) \cdot \sqrt{1/3} = 0,19245\; }[/math] [math]\displaystyle{ \scriptstyle\;\rightarrow\;\delta'/2= 10,89^\circ\;\rightarrow\;\delta'=21,79^\circ }[/math].

2. Two-dimensional Problem

2.1. Derivation of the Formula for Motion Along the x-Axis

For the derivation it is assumed, that the light signal only travels through space regions where the gravitation field is negligible. Hence is suffices to use special relativity and the path of the light signal is a straight line in any inertial frame of reference.

Observation in the rest frame S of the center of mass of our Solar System

The rest frame of the center of mass (barycenter) is a very good^[8] quasi-inertial frame of reference for periods of time in the order of thousands of years, since our solar system needs about 230 million years (galactic year) to move completely around the center of the Milky Way. The space coordinates of this frame of reference form a Cartesian coordinate system.

In the reference frame S [math]\displaystyle{ (x_1|y_1|0|c\,t_1) }[/math] with [math]\displaystyle{ c\,t_1\lt 0 }[/math] and [math]\displaystyle{ (x_1|y_1) \ne (0|0) }[/math] are the (space-time) coordinates at which the star emits a light signal and [math]\displaystyle{ (0|0|0|0) }[/math] are the coordinates at which the astronomer receives the light signal.

In reference frame S the light signal starts at [math]\displaystyle{ t_1\lt 0 }[/math] and stops at time [math]\displaystyle{ t_2=0 }[/math] and therefore the light signal did cover the distance [math]\displaystyle{ d = c\cdot(0-t_1) = -c\,t_1 }[/math] .

In S the path of the light signal is a straight line and it forms an angle [math]\displaystyle{ \delta }[/math] with the x-axis with: [math]\displaystyle{ \sin \delta = \frac{y_1}{d}=\frac{y_1}{-c\,t_1} }[/math]  and [math]\displaystyle{ \cos\delta=\frac{x_1}{-c\,t_1} }[/math]

Observation in the inertial frame of reference S' which is in uniform motion (relative to S) along the x-axis

The origin of the reference frame S' is in uniform motion relative to S with [math]\displaystyle{ (v|0|0) }[/math], i.e. moves along the x-axis, and the x-,y- und z-axes of S' and S are parallel to each other and at time [math]\displaystyle{ \scriptstyle t=t'=0 }[/math] the origins of S and S' coincide. Let [math]\displaystyle{ \beta = \frac{v}{c} , \gamma = \frac{1}{\sqrt{1-\beta^2}} }[/math]

S' now is an equally good quasi-inertial frame of reference as S: the space coordinates form a Cartesian coordinate system and the path of the light signal is a straight line.

According to the Lorentz transformation one gets: [math]\displaystyle{ x_1' = \gamma \cdot(x_1-\beta \cdot c\,t_1) , y_1'=y_1 , z_1'=0 , c\,t_1' = \gamma \cdot (c\,t_1-\beta \cdot x_1) }[/math]

In reference frame S' the light signal starts at [math]\displaystyle{ t_1'\lt 0 }[/math] and stops at time [math]\displaystyle{ t_2'=0 }[/math] and therefore the light signal did cover the distance [math]\displaystyle{ d\,' = c\cdot(0-t_1') = -c\,t_1' }[/math] .

In S' the path of the light signal is a straight line, too. It forms an angle [math]\displaystyle{ \delta' }[/math] with the x'-axis and one gets:

[math]\displaystyle{ \sin \delta' = \frac{y_1'}{d\,'}=\frac{y_1}{-c\,t_1'} =\frac{y_1}{-\gamma \cdot (c\,t_1-\beta \cdot x_1)} =\frac{y_1}{-c\,t_1 \cdot \gamma\cdot \left(1-\beta\cdot\frac{x_1}{c\,t_1}\right)}=\frac{\frac{y_1}{-c\,t_1}}{\gamma\cdot\left(1+\beta\cdot\frac{x_1}{-c\,t_1}\right)} =\frac{\sin \delta}{\gamma\cdot(1+\beta\cdot\cos\delta)} }[/math]

[math]\displaystyle{ \cos\delta'=\frac{x_1'}{-c\,t_1'} =\frac{\gamma \cdot(x_1-\beta \cdot c\,t_1)}{-\gamma \cdot (c\,t_1-\beta \cdot x_1)} =\frac{-c\,t_1 \cdot \gamma \cdot \left ( \frac{x_1}{-c\,t_1}+\beta \right)}{-c\,t_1 \cdot \gamma \cdot \left( 1 + \beta \cdot \frac{x_1}{-c\, t_1} \right) } =\frac{\frac{x_1}{-c\,t_1}+\beta}{1 + \beta \cdot \frac{x_1}{-c\, t_1}} =\frac{\cos \delta +\beta}{1 + \beta \cdot \cos \delta} }[/math]

Hence: [math]\displaystyle{ \tan \delta' = \frac{\sin \delta'}{\cos \delta'}=\frac{\sin \delta}{\gamma\cdot(\cos \delta +\beta)} }[/math]

These are the same formulas as in aberration of light#Explanation.

2.2. Approximate Formula for Motion along the x-Axis in Case of v/c <<1

[math]\displaystyle{ \triangle\delta\;=\;\delta' - \delta\; }[/math] is the change of the angle δ. As β<<1 this change is also very small.

Case I: [math]\displaystyle{ \;\delta\ne\pm 90^\circ\; \rightarrow \;\cos \delta \ne 0 }[/math]

As Δδ<<1 one gets: [math]\displaystyle{ \frac{\tan \delta' - \tan \delta}{\triangle\delta} \approx\frac{d}{d\delta}\tan \delta = \frac{1}{(\cos \delta)^2}\; \rightarrow \; \triangle\delta\;=\;(\cos \delta)^2 \cdot (\tan \delta' - \tan \delta) }[/math]

As β<<1 one gets: [math]\displaystyle{ \tan\delta'=\frac {\sin \delta}{\gamma(\cos \delta +\beta)} \approx \frac {\sin \delta}{\cos \delta +\beta} = \frac{\sin \delta}{\cos \delta \cdot \left(1+\frac{\beta}{\cos \delta}\right)} \approx \tan \delta \cdot \left(1-\frac{\beta}{\cos \delta}\right) }[/math]

Therefore [math]\displaystyle{ \triangle\delta\;=\;(\cos \delta)^2 \cdot (\tan \delta' - \tan \delta) = (\cos \delta)^2 \cdot \tan \delta \left(1-\frac{\beta}{\cos \delta}\;-1\right) = - \cos \delta \cdot \tan \delta \cdot \beta = -\beta \cdot \sin \delta }[/math]

Case IIa: [math]\displaystyle{ \;\delta\;=90^\circ\; }[/math], hence: [math]\displaystyle{ \tan \delta' =\frac{\sin 90^\circ}{\gamma\cdot(\cos 90^\circ + \beta)}= \frac{1}{\gamma \cdot \beta}\;\approx \frac {1}{\beta} \quad \rightarrow \quad \cot \delta' = \beta \quad \rightarrow \quad \delta' = \arccot \beta \approx \frac{\pi}{2} - \beta }[/math]

and therefore: [math]\displaystyle{ \triangle\delta = \delta' - \delta = -\beta \quad \left(= -\beta \cdot \sin(90^\circ)\right) }[/math]

Case IIb: [math]\displaystyle{ \;\delta\;=-90^\circ\; }[/math], and hence: [math]\displaystyle{ \tan \delta' = \frac{-1}{\gamma \cdot \beta}\;\approx -\frac {1}{\beta} \quad \rightarrow \quad \cot \delta' = -\beta \quad \rightarrow \quad \delta' = \arccot \beta \approx -\frac{\pi}{2} + \beta \quad }[/math]    ^[9]

Hence: [math]\displaystyle{ \triangle\delta = \delta' - \delta = +\beta\quad \left(= -\beta \cdot \sin(-90^\circ)\right) }[/math]

Conclusion:The change of the angle Δδ = δ'-δ in the case of β = v/c << 1 can be described by the approximate formula [math]\displaystyle{ \triangle\delta = -\frac{v}{c} \cdot \sin \delta\; }[/math] resp. in the degree measure [math]\displaystyle{ \triangle\delta = -\frac{v}{c} \cdot \sin \delta \cdot \frac{180^\circ}{\pi} }[/math]

2.3. Symmetric form of the (Exact) Formula for Motion Along the x-Axis

With help of tangent half-angle formula [math]\displaystyle{ \scriptstyle \tan (\alpha/2)=\sin\alpha/(1+\cos\alpha) }[/math]  one can prove the symmetric form: [math]\displaystyle{ \tan \frac{\delta'}{2}=\sqrt{\frac{1-\beta}{1+\beta}}\cdot\tan\frac{\delta}{2} }[/math]   (derivation found in a SR-textbook^[10])

[math]\displaystyle{ \tan \frac{\delta'}{2}=\frac{\sin \delta'}{1+\cos \delta'} =\frac{\frac{\sin \delta}{\gamma\cdot(1+\beta\cdot\cos\delta)}}{\frac{1 + \beta \cdot \cos \delta}{1 + \beta \cdot \cos \delta}+\frac{\cos \delta +\beta}{1 + \beta \cdot \cos \delta}} =\frac{\sin \delta}{\gamma\cdot(1 + \beta \cdot \cos \delta + \cos \delta +\beta)}=\frac{\sin \delta}{\gamma\cdot(1 + \beta)\cdot(1+ \cos \delta)} =\frac{\tan \frac{\delta}{2}}{\gamma\cdot(1+ \beta)} }[/math]

And as [math]\displaystyle{ \frac{1}{\gamma\cdot(1+\beta)} =\frac{\sqrt{1-\beta^2}}{1+\beta} =\frac{\sqrt{(1+\beta)(1-\beta)}}{1+\beta} =\sqrt{\frac{1-\beta}{1+\beta}} }[/math] the symmetric form follows.

2.4. Formula for Motion Along the y-Axis

Let [math]\displaystyle{ \theta }[/math] be the angle between the light ray (=path of the light signal which is a straight line) and the y-axis whereby θ is positive if the y-axis would have to rotate counter-clockwise to coincide with the light ray. Then the derivation of the formula of angle θ' for the motion along the y-axis is the same as the derivation of the formula of angle δ' for the motion along the x-axis.

Hence: [math]\displaystyle{ \tan\theta\,' = \frac{\sin\theta}{\gamma\cdot(\cos\theta+\beta)} }[/math]

The symmetric form is: [math]\displaystyle{ \tan \frac{\theta\,'}{2}=\sqrt{\frac{1-\beta}{1+\beta}}\cdot\tan\frac{\theta}{2} }[/math] and the approximate formula is: [math]\displaystyle{ \triangle\theta = -\beta\cdot\sin\theta }[/math]

As [math]\displaystyle{ \theta=\delta-90^\circ }[/math] and as [math]\displaystyle{ \scriptstyle\sin(\delta-90^{\circ})=-\sin(90^\circ-\delta)=-\cos\delta\;,\;\cos(\delta-90^\circ)=\cos(90^\circ-\delta)=\sin\delta }[/math] and [math]\displaystyle{ \scriptstyle\tan(\delta-90^\circ)=-\tan(90^\circ-\delta)=-\cot\delta }[/math]  one gets:

[math]\displaystyle{ \tan(\delta'-90^\circ) = \frac{\sin(\delta-90^\circ)}{\gamma\cdot\left(\cos(\delta - 90 ^\circ)+\beta\right)} }[/math] and therefore:  [math]\displaystyle{ -\cot\delta' = \frac{-\cos\delta}{\gamma\cdot(\sin\delta+\beta)} }[/math] and hence [math]\displaystyle{ \cot\delta' = \frac{\cos\delta}{\gamma\cdot(\sin\delta+\beta)} }[/math]

Since [math]\displaystyle{ \cot\delta'=\frac{1}{\tan\delta'} }[/math]  one also gets: [math]\displaystyle{ \tan\delta' = \frac{\gamma\cdot(\sin\delta+\beta)}{\cos\delta} }[/math]

And the symmetric form is: [math]\displaystyle{ \tan \frac{\delta'-90^\circ}{2}=\sqrt{\frac{1-\beta}{1+\beta}}\cdot\tan\frac{\delta-90^\circ}{2} }[/math]

And as [math]\displaystyle{ \scriptstyle\triangle\theta=(\delta'-90^\circ)-(\delta-90^\circ)=\triangle\delta }[/math]  the approximate formula is: [math]\displaystyle{ \triangle\delta = \triangle\theta =-\beta\cdot\sin(\delta-90^\circ)=+\beta\cdot\cos\delta }[/math]   

2.5. Formula for Motion Along a Ray Lying in the x-y-Plane with Direction Vector (cos α | sin α)

With the same reasoning as above one gets the formula: [math]\displaystyle{ \tan(\delta'-\alpha) = \frac{\sin(\delta-\alpha)}{\gamma\cdot\left(\cos(\delta-\alpha)+\beta\right)} }[/math]

The symmetric form is: [math]\displaystyle{ \tan \frac{\delta'-\alpha}{2}=\sqrt{\frac{1-\beta}{1+\beta}}\cdot\tan\frac{\delta-\alpha}{2} }[/math]

The approximate formula is: [math]\displaystyle{ \triangle\delta = - \beta\cdot\sin(\delta-\alpha) }[/math]  and in the degree measure: [math]\displaystyle{ \triangle\delta = -\frac{v}{c}\cdot\sin(\delta-\alpha)\cdot\frac{180^\circ}{\pi} }[/math]

3. Three-dimensional Problem

Heliocentric ecliptic coordinates. https://handwiki.org/wiki/index.php?curid=1662364

Earth-centered Ecliptic coordinates. https://handwiki.org/wiki/index.php?curid=1575025

4. Application: Aberration in Astronomy

The stellar aberration is purely an effect of the change of the reference frame. The astronomer orbits (with Earth) around the Sun and furthermore rotates around the axis of Earth. His current rest frame S' therefore has different velocities relative to the rest frame S of the barycenter of the Solar System at different times. Hence the astronomer observes that the position of the star changes. The formula is derived under the condition that the change of the position of the star and of Earth is negligible in the period of observation.^[11] That is correct for almost all stars: the amplitude of the parallax of a star, for a distance of ≥ n parsec, is ≤ 1/n".

4.1. Stellar Aberration Due to the Orbit of Earth (Around the Sun)

The mean orbital speed of Earth is [math]\displaystyle{ v_e = \frac{2 \cdot \pi \cdot 1\,AE}{365,25\,d} = 29,78\,km/s }[/math], and therefore [math]\displaystyle{ \frac{v_e}{c} = 0,00009935 }[/math].

-> [math]\displaystyle{ \frac{v}{c} \cdot \frac{180^\circ}{\pi} = 20,5^{\prime\prime} }[/math].

[math]\displaystyle{ k_A= 20,5^{\prime\prime} }[/math] is dubbed constant of aberration for the annual aberration.^[12]

4.2. Stellar Aberration Due to Earth's Rotation

An astronomer at the latitude [math]\displaystyle{ \varphi }[/math] rotates in 24 hours around the axis of Earth. His speed of rotation is therefore [math]\displaystyle{ v_r= \frac{\cos \varphi \cdot 40000\,km}{1\,d} = \cos \varphi \cdot 463\,m/s }[/math]. Hence [math]\displaystyle{ \frac{v_r}{c} = \cos \varphi \cdot 1,54\cdot10^{-6} }[/math]. Form this so called diurnal aberration one gets an additional contribution of (at max.) [math]\displaystyle{ \cos \varphi \cdot 0,32^{\prime\prime} }[/math].

4.3. Stellar Aberration Due the Orbit of Our Solar System Around the Center of the Milky Way

The rest frame of the center of mass of our solar system isn't a perfect inertial frame of reference since our solar system orbits around the center of the Milky Way. An estimation for the time of period of circulation is 230 million years (estimations vary between 225 and 250 million years).^[13][14] As the estimation for the distance between our solar system and the center of the Milky Way is about 28000 Ly, the assumed orbital speed of our solar system is [math]\displaystyle{ \scriptstyle v = \frac{2\pi \cdot 280000 \cdot 9,461\cdot10^{15}\,m}{230\cdot 10^{6} \cdot 365,25 \cdot 24 \cdot 3600} \approx\, 230\,km/s }[/math]. This would cause an aberration ellipse with a major semiaxis of 2,6' (arcminutes). Therefore, in one year the aberration angle could change (at max.) [math]\displaystyle{ \scriptstyle 2,6^\prime \cdot \frac{2 \pi \cdot 1\,a}{230000000\,a} }[/math] = 4,3 µas (microarcseconds). This very small value isn't detectable now, perhaps it's possible with the planned mission of the Gaia spacecraft.^[15]