1. Van Kampen's Theorem for Fundamental Groups^[1]

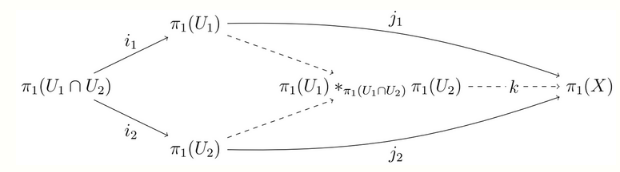
Let X be a topological space which is the union of two open and path connected subspaces U₁, U₂. Suppose U₁ ∩ U₂ is path connected and nonempty, and let x₀ be a point in U₁ ∩ U₂ that will be used as the base of all fundamental groups. The inclusion maps of U₁ and U₂ into X induce group homomorphisms [math]\displaystyle{ j_1:\pi_1(U_1,x_0)\to \pi_1(X,x_0) }[/math] and [math]\displaystyle{ j_2:\pi_1(U_2,x_0)\to \pi_1(X,x_0) }[/math]. Then X is path connected and [math]\displaystyle{ j_1 }[/math] and [math]\displaystyle{ j_2 }[/math] form a commutative pushout diagram:

the natural morphism k is an isomorphism, that is, the fundamental group of X is the free product of the fundamental groups of U₁ and U₂ with amalgamation of [math]\displaystyle{ \pi_1(U_1\cap U_2, x_0) }[/math].^[2]

Usually the morphisms induced by inclusion in this theorem are not themselves injective, and the more precise version of the statement is in terms of pushouts of groups.

1.1. Van Kampen's Theorem for Fundamental Groupoids

Unfortunately, the theorem as given above does not compute the fundamental group of the circle, which is the most important basic example in algebraic topology. The reason is that the circle cannot be realised as the union of two open sets with connected intersection. This problem can be resolved by working with the fundamental groupoid [math]\displaystyle{ \pi_1(X,A) }[/math] on a set A of base points, chosen according to the geometry of the situation. Thus for the circle, one uses two base points.^[3]

This groupoid consists of homotopy classes relative to the end points of paths in X joining points of A ∩ X. In particular, if X is a contractible space, and A consists of two distinct points of X, then [math]\displaystyle{ \pi_1(X,A) }[/math] is easily seen to be isomorphic to the groupoid often written [math]\displaystyle{ \mathcal I }[/math] with two vertices and exactly one morphism between any two vertices. This groupoid plays a role in the theory of groupoids analogous to that of the group of integers in the theory of groups.^[4] The groupoid [math]\displaystyle{ \mathcal I }[/math] also allows for groupoids a notion of homotopy: it is a unit interval object in the category of groupoids.

A connected union of two non connected spaces, with set of base points. https://handwiki.org/wiki/index.php?curid=1319466

The category of groupoids admits all colimits, and in particular all pushouts.

Theorem. Let the topological space X be covered by the interiors of two subspaces X₁, X₂ and let A be a set which meets each path component of X₁, X₂ and X₀ = X₁ ∩ X₂. Then A meets each path component of X and the diagram P of morphisms induced by inclusion

is a pushout diagram in the category of groupoids.^[5]

This theorem gives the transition from topology to algebra, in determining completely the fundamental groupoid [math]\displaystyle{ \pi_1(X,A) }[/math]; one then has to use algebra and combinatorics to determine a fundamental group at some basepoint.

One interpretation of the theorem is that it computes homotopy 1-types. To see its utility, one can easily find cases where X is connected but is the union of the interiors of two subspaces, each with say 402 path components and whose intersection has say 1004 path components. The interpretation of this theorem as a calculational tool for "fundamental groups" needs some development of 'combinatorial groupoid theory'.^[6][7] This theorem implies the calculation of the fundamental group of the circle as the group of integers, since the group of integers is obtained from the groupoid [math]\displaystyle{ \mathcal I }[/math] by identifying, in the category of groupoids, its two vertices.

There is a version of the last theorem when X is covered by the union of the interiors of a family [math]\displaystyle{ \{U_\lambda : \lambda \in \Lambda\} }[/math] of subsets.^[8][9]

The conclusion is that if A meets each path component of all 1,2,3-fold intersections of the sets [math]\displaystyle{ U_\lambda }[/math], then A meets all path components of X and the diagram

[math]\displaystyle{ \bigsqcup_{(\lambda,\mu) \in \Lambda^2} \pi_1(U_\lambda \cap U_\mu, A) \rightrightarrows \bigsqcup_{\lambda \in \Lambda} \pi_1(U_\lambda, A)\rightarrow \pi_1(X,A) }[/math]

of morphisms induced by inclusions is a coequaliser in the category of groupoids.

[...] people still obstinately persist, when calculating with fundamental groups, in fixing a single base point, instead of cleverly choosing a whole packet of points which is invariant under the symmetries of the situation, which thus get lost on the way. In certain situations (such as descent theorems for fundamental groups à la van Kampen) it is much more elegant, even indispensable for understanding something, to work with fundamental groupoids with respect to a suitable packet of base points [...]

2. Equivalent Formulations

In the language of combinatorial group theory, if [math]\displaystyle{ X }[/math] is a topological space; [math]\displaystyle{ U }[/math] and [math]\displaystyle{ V }[/math] are open, path connected subspaces of [math]\displaystyle{ X }[/math]; [math]\displaystyle{ U\cap V }[/math] is nonempty and path-connected; and [math]\displaystyle{ w\in U\cap V }[/math]; then [math]\displaystyle{ \pi_1(X,w) }[/math] is the free product with amalgamation of [math]\displaystyle{ \pi_1(U,w) }[/math] and [math]\displaystyle{ \pi_1(V,w) }[/math], with respect to the (not necessarily injective) homomorphisms [math]\displaystyle{ I:\pi_1(U\cap V, w)\to \pi_1(U,w) }[/math] and [math]\displaystyle{ J:\pi_1(U\cap V, w)\to \pi_1(V,w) }[/math]. Given group presentations:

[math]\displaystyle{ \begin{align} \pi_1(U,w) &= \langle u_1,\cdots,u_k \mid\alpha_1,\cdots,\alpha_l\rangle \\ \pi_1(V,w) &= \langle v_1,\cdots,v_m \mid \beta_1,\cdots,\beta_n\rangle \\ \pi_1(U\cap V,w) &= \langle w_1,\cdots,w_p \mid \gamma_1,\cdots,\gamma_q\rangle \end{align} }[/math]

the amalgamation can be presented^[10] as

[math]\displaystyle{ \pi_1(X,w) = \left \langle u_1,\cdots,u_k, v_1,\cdots,v_m \left | \alpha_1,\cdots,\alpha_l, \beta_1,\cdots,\beta_n, I(w_1)J(w_1)^{-1},\cdots,I(w_p)J(w_p)^{-1} \right. \right \rangle. }[/math]

In category theory, [math]\displaystyle{ \pi_1(X,w) }[/math] is the pushout, in the category of groups, of the diagram:

[math]\displaystyle{ \pi_1(U,w)\gets\pi_1(U\cap V,w)\to\pi_1(V,w). }[/math]

3. Examples

3.1. 2-Sphere

One can use Van Kampen's theorem to calculate fundamental groups for topological spaces that can be decomposed into simpler spaces. For example, consider the sphere [math]\displaystyle{ S^2 }[/math]. Pick open sets [math]\displaystyle{ A=S^2\setminus \{n\} }[/math] and [math]\displaystyle{ B=S^2\setminus \{s\} }[/math] where n and s denote the north and south poles respectively. Then we have the property that A, B and A ∩ B are open path connected sets. Thus we can see that there is a commutative diagram including A ∩ B into A and B and then another inclusion from A and B into [math]\displaystyle{ S^2 }[/math] and that there is a corresponding diagram of homomorphisms between the fundamental groups of each subspace. Applying Van Kampen's theorem gives the result

[math]\displaystyle{ \pi_1(S^2)=\pi_1(A)\cdot\pi_1(B)/\ker(\Phi). }[/math]

However A and B are both homeomorphic to R² which is simply connected, so both A and B have trivial fundamental groups. It is clear from this that the fundamental group of [math]\displaystyle{ S^2 }[/math] is trivial.

3.2. Wedge Sum of Spaces

Given two pointed spaces [math]\displaystyle{ (X,x) }[/math] and [math]\displaystyle{ (Y,y) }[/math] we can form their wedge sum, [math]\displaystyle{ (X\vee Y,p) }[/math], by taking the quotient of [math]\displaystyle{ X \coprod Y }[/math] by identifying their two basepoints.

If [math]\displaystyle{ x }[/math] admits a contractible open neighborhood [math]\displaystyle{ U \subset X }[/math] and [math]\displaystyle{ y }[/math] admits a contractible open neighborhood [math]\displaystyle{ V \subset Y }[/math] (which is the case if, for instance, [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are CW complexes), then we can apply the van Kampen theorem to [math]\displaystyle{ X \vee Y }[/math] by taking [math]\displaystyle{ X \vee V }[/math] and [math]\displaystyle{ U \vee Y }[/math] as the two open sets and we conclude that the fundamental group of the wedge is the free product of the fundamental groups of the two spaces we started with:

[math]\displaystyle{ \pi_1(X\vee Y, p)\cong \pi_1(X,x)*\pi_1(Y,y) }[/math].

3.3. Orientable Genus g Surfaces

A more complicated example is the calculation of the fundamental group of a genus n orientable surface S, otherwise known as the genus n surface group. One can construct S using its standard fundamental polygon. For the first open set A, pick a disk within the center of the polygon. Pick B to be the complement in S of the center point of A. Then the intersection of A and B is an annulus, which is known to be homotopy equivalent to (and so has the same fundamental group as) a circle. Then [math]\displaystyle{ \pi_1(A \cap B)=\pi_1(S^1) }[/math], which is the integers, and [math]\displaystyle{ \pi_1(A)=\pi_1(D^2)={1} }[/math]. Thus the inclusion of [math]\displaystyle{ \pi_1(A \cap B) }[/math] into [math]\displaystyle{ \pi_1(A) }[/math] sends any generator to the trivial element. However, the inclusion of [math]\displaystyle{ \pi_1(A \cap B) }[/math] into [math]\displaystyle{ \pi_1(B) }[/math] is not trivial. In order to understand this, first one must calculate [math]\displaystyle{ \pi_1(B) }[/math]. This is easily done as one can deformation retract B (which is S with one point deleted) onto the edges labeled by

[math]\displaystyle{ A_1 B_1 A_1^{-1} B_1^{-1} A_2 B_2 A_2^{-1} B_2^{-1} \cdots A_n B_n A_n^{-1} B_n^{-1}. }[/math]

This space is known to be the wedge sum of 2n circles (also called a bouquet of circles), which further is known to have fundamental group isomorphic to the free group with 2n generators, which in this case can be represented by the edges themselves: [math]\displaystyle{ \{A_1,B_1,\cdots,A_n,B_n\} }[/math]. We now have enough information to apply Van Kampen's theorem. The generators are the loops [math]\displaystyle{ \{A_1,B_1,\cdots,A_n,B_n\} }[/math] (A is simply connected, so it contributes no generators) and there is exactly one relation:

[math]\displaystyle{ A_1 B_1 A_1^{-1} B_1^{-1} A_2 B_2 A_2^{-1} B_2^{-1} \cdots A_n B_n A_n^{-1} B_n^{-1} = 1. }[/math]

Using generators and relations, this group is denoted

[math]\displaystyle{ \left \langle A_1,B_1,\cdots,A_n,B_n\left | A_1B_1A_1^{-1}B_1^{-1}\cdots A_nB_nA_n^{-1}B_n^{-1}\right. \right \rangle. }[/math]

4. Generalizations

As explained above, this theorem was extended by Ronald Brown to the non-connected case by using the fundamental groupoid [math]\displaystyle{ \pi_1 (X,A) }[/math] on a set A of base points. The theorem for arbitrary covers, with the restriction that A meets all threefold intersections of the sets of the cover, is given in the paper by Brown and Abdul Razak Salleh.^[11] The theorem and proof for the fundamental group, but using some groupoid methods, are also given in J. Peter May's book.^[12] The version that allows more than two overlapping sets but with A a singleton is also given in Allen Hatcher's book below, theorem 1.20.

Applications of the fundamental groupoid on a set of base points to the Jordan curve theorem, covering spaces, and orbit spaces are given in Ronald Brown's book.^[13] In the case of orbit spaces, it is convenient to take A to include all the fixed points of the action. An example here is the conjugation action on the circle.

References to higher-dimensional versions of the theorem which yield some information on homotopy types are given in an article on higher-dimensional group theories and groupoids.^[14] Thus a 2-dimensional van Kampen theorem which computes nonabelian second relative homotopy groups was given by Ronald Brown and Philip J. Higgins.^[15] A full account and extensions to all dimensions are given by Brown, Higgins, and Rafael Sivera,^[16] while an extension to n-cubes of spaces is given by Ronald Brown and Jean-Louis Loday.^[17]

Fundamental groups also appear in algebraic geometry and are the main topic of Alexander Grothendieck's first Séminaire de géométrie algébrique (SGA1). A version of van Kampen's theorem appears there, and is proved along quite different lines than in algebraic topology, namely by descent theory. A similar proof works in algebraic topology.^[18]