
Video Upload Options
In logic and mathematics, the converse of a categorical or implicational statement is the result of reversing its two constituent statements. For the implication P → Q, the converse is Q → P. For the categorical proposition All S are P, the converse is All P are S. Either way, the truth of the converse is generally independent from that of the original statement.
1. Implicational Converse
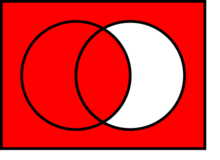
(the white area shows where the statement is false)
Let S be a statement of the form P implies Q (P → Q). Then the converse of S is the statement Q implies P (Q → P). In general, the truth of S says nothing about the truth of its converse,[1] unless the antecedent P and the consequent Q are logically equivalent.
For example, consider the true statement "If I am a human, then I am mortal." The converse of that statement is "If I am mortal, then I am a human," which is not necessarily true.
On the other hand, the converse of a statement with mutually inclusive terms remains true, given the truth of the original proposition. This is equivalent to saying that the converse of a definition is true. Thus, the statement "If I am a triangle, then I am a three-sided polygon" is logically equivalent to "If I am a three-sided polygon, then I am a triangle", because the definition of "triangle" is "three-sided polygon".
A truth table makes it clear that S and the converse of S are not logically equivalent, unless both terms imply each other:
| [math]\displaystyle{ P }[/math] | [math]\displaystyle{ Q }[/math] | [math]\displaystyle{ P \rightarrow Q }[/math] | [math]\displaystyle{ P \leftarrow Q }[/math] (converse) |
| True | True | True | True |
| True | False | False | True |
| False | True | True | False |
| False | False | True | True |
Going from a statement to its converse is the fallacy of affirming the consequent. However, if the statement S and its converse are equivalent (i.e., P is true if and only if Q is also true), then affirming the consequent will be valid.
Converse implication is logically equivalent to the disjunction of [math]\displaystyle{ P }[/math] and [math]\displaystyle{ \neg Q }[/math]
In natural language, this could be rendered "not Q without P".
1.1. Converse of a Theorem
In mathematics, the converse of a theorem of the form P → Q will be Q → P. The converse may or may not be true, and even if true, the proof may be difficult. For example, the Four-vertex theorem was proved in 1912, but its converse was proved only in 1997.[2]
In practice, when determining the converse of a mathematical theorem, aspects of the antecedent may be taken as establishing context. That is, the converse of "Given P, if Q then R" will be "Given P, if R then Q". For example, the Pythagorean theorem can be stated as:
Given a triangle with sides of length [math]\displaystyle{ a }[/math], [math]\displaystyle{ b }[/math], and [math]\displaystyle{ c }[/math], if the angle opposite the side of length [math]\displaystyle{ c }[/math] is a right angle, then [math]\displaystyle{ a^2 + b^2 = c^2 }[/math].
The converse, which also appears in Euclid's Elements (Book I, Proposition 48), can be stated as:
Given a triangle with sides of length [math]\displaystyle{ a }[/math], [math]\displaystyle{ b }[/math], and [math]\displaystyle{ c }[/math], if [math]\displaystyle{ a^2 + b^2 = c^2 }[/math], then the angle opposite the side of length [math]\displaystyle{ c }[/math] is a right angle.
1.2. Converse of a Relation

If [math]\displaystyle{ R }[/math] is a binary relation with [math]\displaystyle{ R \subseteq A \times B, }[/math] then the converse relation [math]\displaystyle{ R^T = \{ (b,a) : (a,b) \in R \} }[/math] is also called the transpose.[3]
2. Notation
The converse of the implication P → Q may be written Q → P, [math]\displaystyle{ P \leftarrow Q }[/math], but may also be notated [math]\displaystyle{ P \subset Q }[/math], or "Bpq" (in Bocheński notation).
3. Categorical Converse
In traditional logic, the process of switching the subject term with the predicate term is called conversion. For example going from "No S are P" to its converse "No P are S". In the words of Asa Mahan:
"The original proposition is called the exposita; when converted, it is denominated the converse. Conversion is valid when, and only when, nothing is asserted in the converse which is not affirmed or implied in the exposita."[4]
The "exposita" is more usually called the "convertend." In its simple form, conversion is valid only for E and I propositions:[5]
| Type | Convertend | Simple converse | Converse per accidens (valid if P exists) |
|---|---|---|---|
| A | All S are P | not valid | Some P is S |
| E | No S is P | No P is S | Some P is not S |
| I | Some S is P | Some P is S | – |
| O | Some S is not P | not valid | – |
The validity of simple conversion only for E and I propositions can be expressed by the restriction that "No term must be distributed in the converse which is not distributed in the convertend."[6] For E propositions, both subject and predicate are distributed, while for I propositions, neither is.
For A propositions, the subject is distributed while the predicate is not, and so the inference from an A statement to its converse is not valid. As an example, for the A proposition "All cats are mammals", the converse "All mammals are cats" is obviously false. However, the weaker statement "Some mammals are cats" is true. Logicians define conversion per accidens to be the process of producing this weaker statement. Inference from a statement to its converse per accidens is generally valid. However, as with syllogisms, this switch from the universal to the particular causes problems with empty categories: "All unicorns are mammals" is often taken as true, while the converse per accidens "Some mammals are unicorns" is clearly false.
In first-order predicate calculus, All S are P can be represented as [math]\displaystyle{ \forall x. S(x) \to P(x) }[/math].[7] It is therefore clear that the categorical converse is closely related to the implicational converse, and that S and P cannot be swapped in All S are P.
References
- Taylor, Courtney. "What Are the Converse, Contrapositive, and Inverse?" (in en). https://www.thoughtco.com/converse-contrapositive-and-inverse-3126458.
- Shonkwiler, Clay (October 6, 2006). "The Four Vertex Theorem and its Converse". https://www.math.colostate.edu/~clayton/research/talks/FourVertexPrint.pdf.
- Gunther Schmidt & Thomas Ströhlein (1993) Relations and Graphs, page 9, Springer books
- Asa Mahan (1857) The Science of Logic: or, An Analysis of the Laws of Thought, p. 82. https://books.google.com/books?id=J_wtAAAAMAAJ&pg=PA82
- William Thomas Parry and Edward A. Hacker (1991), Aristotelian Logic, SUNY Press, p. 207. https://books.google.com/books?id=3Sg84H6B-m4C&pg=PA207
- James H. Hyslop (1892), The Elements of Logic, C. Scribner's sons, p. 156.
- Gordon Hunnings (1988), The World and Language in Wittgenstein's Philosophy, SUNY Press, p. 42. https://books.google.com/books?id=5XXz7B2PLRsC&pg=PA42




