
Video Upload Options
In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to (i.e., forming a right angle with) a line containing the base (the side opposite the vertex). This line containing the opposite side is called the extended base of the altitude. The intersection of the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called "the altitude", is the distance between the extended base and the vertex. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude at that vertex. It is a special case of orthogonal projection. Altitudes can be used in the computation of the area of a triangle: one half of the product of an altitude's length and its base's length equals the triangle's area. Thus, the longest altitude is perpendicular to the shortest side of the triangle. The altitudes are also related to the sides of the triangle through the trigonometric functions. In an isosceles triangle (a triangle with two congruent sides), the altitude having the incongruent side as its base will have the midpoint of that side as its foot. Also the altitude having the incongruent side as its base will be the angle bisector of the vertex angle. It is common to mark the altitude with the letter h (as in height), often subscripted with the name of the side the altitude is drawn to. In a right triangle, the altitude drawn to the hypotenuse c divides the hypotenuse into two segments of lengths p and q. If we denote the length of the altitude by hc, we then have the relation For acute and right triangles the feet of the altitudes all fall on the triangle's sides (not extended). In an obtuse triangle (one with an obtuse angle), the foot of the altitude to the obtuse-angled vertex falls in the interior of the opposite side, but the feet of the altitudes to the acute-angled vertices fall on the opposite extended side, exterior to the triangle. This is illustrated in the adjacent diagram: in this obtuse triangle, an altitude dropped perpendicularly from the top vertex, which has an acute angle, intersects the extended horizontal side outside the triangle.
1. Orthocenter

The three (possibly extended) altitudes intersect in a single point, called the orthocenter of the triangle, usually denoted by H.[1][2] The orthocenter lies inside the triangle if and only if the triangle is acute (i.e. does not have an angle greater than or equal to a right angle). If one angle is a right angle, the orthocenter coincides with the vertex at the right angle.[2]
Let A, B, C denote the vertices and also the angles of the triangle, and let a = |BC|, b = |CA|, c = |AB| be the side lengths. The orthocenter has trilinear coordinates[3]
[math]\displaystyle{ \sec A:\sec B:\sec C = \cos A-\sin B \sin C:\cos B-\sin C \sin A:\cos C-\sin A\sin B, }[/math]
and barycentric coordinates
- [math]\displaystyle{ \displaystyle (a^2+b^2-c^2)(a^2-b^2+c^2) : (a^2+b^2-c^2)(-a^2+b^2+c^2) : (a^2-b^2+c^2)(-a^2+b^2+c^2) }[/math]
- [math]\displaystyle{ =\tan A:\tan B:\tan C. }[/math]
Since barycentric coordinates are all positive for a point in a triangle's interior but at least one is negative for a point in the exterior, and two of the barycentric coordinates are zero for a vertex point, the barycentric coordinates given for the orthocenter show that the orthocenter is in an acute triangle's interior, on the right-angled vertex of a right triangle, and exterior to an obtuse triangle.
In the complex plane, let the points A, B and C represent the numbers [math]\displaystyle{ z_A }[/math], [math]\displaystyle{ z_B }[/math] and, respectively, [math]\displaystyle{ z_C }[/math] and assume that the circumcenter of triangle ABC is located at the origin of the plane. Then, the complex number
- [math]\displaystyle{ z_H=z_A+z_B+z_C }[/math]
is represented by the point H, namely the orthocenter of triangle ABC.[4] From this, the following characterizations of the orthocenter H by means of free vectors can be established straightforwardly:
- [math]\displaystyle{ \vec{OH}=\sum\limits_{\scriptstyle\rm cyclic}\vec{OA},\qquad2\cdot\vec{HO}=\sum\limits_{\scriptstyle\rm cyclic}\vec{HA}. }[/math]
The first of the previous vector identities is also known as the problem of Sylvester, proposed by James Joseph Sylvester.[5]
1.1. Properties
Let D, E, and F denote the feet of the altitudes from A, B, and C respectively. Then:
- The product of the lengths of the segments that the orthocenter divides an altitude into is the same for all three altitudes:[6][7]
- [math]\displaystyle{ AH \cdot HD = BH \cdot HE = CH \cdot HF. }[/math]
- The circle centered at H having radius the square root of this constant is the triangle's polar circle.[8]
- The sum of the ratios on the three altitudes of the distance of the orthocenter from the base to the length of the altitude is 1:[9] (This property and the next one are applications of a more general property of any interior point and the three cevians through it.)
- [math]\displaystyle{ \frac{HD}{AD} + \frac{HE}{BE} + \frac{HF}{CF} = 1. }[/math]
- The sum of the ratios on the three altitudes of the distance of the orthocenter from the vertex to the length of the altitude is 2:[9]
- [math]\displaystyle{ \frac{AH}{AD} + \frac{BH}{BE} + \frac{CH}{CF} = 2. }[/math]
- The isogonal conjugate of the orthocenter is the circumcenter of the triangle.[10]
- The isotomic conjugate of the orthocenter is the symmedian point of the anticomplementary triangle.[11]
- Four points in the plane, such that one of them is the orthocenter of the triangle formed by the other three, is called an orthocentric system or orthocentric quadrangle.
1.2. Relation with Circles and Conics
Denote the circumradius of the triangle by R. Then[12][13]
- [math]\displaystyle{ a^2+b^2+c^2+AH^2+BH^2+CH^2 = 12R^2. }[/math]
In addition, denoting r as the radius of the triangle's incircle, ra, rb, and rc as the radii of its excircles, and R again as the radius of its circumcircle, the following relations hold regarding the distances of the orthocenter from the vertices:[14]
- [math]\displaystyle{ r_a+r_b+r_c+r=AH+BH+CH+2R, }[/math]
- [math]\displaystyle{ r_a^2+r_b^2+r_c^2+r^2=AH^2+BH^2+CH^2+(2R)^2. }[/math]
If any altitude, for example, AD, is extended to intersect the circumcircle at P, so that AP is a chord of the circumcircle, then the foot D bisects segment HP:[7]
- [math]\displaystyle{ HD = DP. }[/math]
The directrices of all parabolas that are externally tangent to one side of a triangle and tangent to the extensions of the other sides pass through the orthocenter.[15]
A circumconic passing through the orthocenter of a triangle is a rectangular hyperbola.[16]
1.3. Relation to Other Centers, the Nine-Point Circle
The orthocenter H, the centroid G, the circumcenter O, and the center N of the nine-point circle all lie on a single line, known as the Euler line.[17] The center of the nine-point circle lies at the midpoint of the Euler line, between the orthocenter and the circumcenter, and the distance between the centroid and the circumcenter is half of that between the centroid and the orthocenter:[18]
- [math]\displaystyle{ OH=2NH, }[/math]
- [math]\displaystyle{ 2OG=GH. }[/math]
The orthocenter is closer to the incenter I than it is to the centroid, and the orthocenter is farther than the incenter is from the centroid:
- [math]\displaystyle{ HI \lt HG, }[/math]
- [math]\displaystyle{ HG \gt IG. }[/math]
In terms of the sides a, b, c, inradius r and circumradius R,[19]
- [math]\displaystyle{ OH^2 = R^2 -8R^2 \cos A \cos B \cos C=9R^2-(a^2+b^2+c^2), }[/math][20]:p. 449
- [math]\displaystyle{ HI^2 = 2r^2 -4R^2 \cos A \cos B \cos C. }[/math]
2. Orthic Triangle
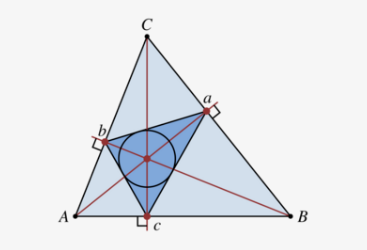
If the triangle ABC is oblique (does not contain a right-angle), the pedal triangle of the orthocenter of the original triangle is called the orthic triangle or altitude triangle. That is, the feet of the altitudes of an oblique triangle form the orthic triangle, DEF. Also, the incenter (the center of the inscribed circle) of the orthic triangle DEF is the orthocenter of the original triangle ABC.[21]
Trilinear coordinates for the vertices of the orthic triangle are given by
- D = 0 : sec B : sec C
- E = sec A : 0 : sec C
- F = sec A : sec B : 0.
The extended sides of the orthic triangle meet the opposite extended sides of its reference triangle at three collinear points.[21][22][23]
In any acute triangle, the inscribed triangle with the smallest perimeter is the orthic triangle.[24] This is the solution to Fagnano's problem, posed in 1775.[25] The sides of the orthic triangle are parallel to the tangents to the circumcircle at the original triangle's vertices.[26]
The orthic triangle of an acute triangle gives a triangular light route.[27]
The tangent lines of the nine-point circle at the midpoints of the sides of ABC are parallel to the sides of the orthic triangle, forming a triangle similar to the orthic triangle.[28]
The orthic triangle is closely related to the tangential triangle, constructed as follows: let LA be the line tangent to the circumcircle of triangle ABC at vertex A, and define LB and LC analogously. Let A" = LB ∩ LC, B" = LC ∩ LA, C" = LC ∩ LA. The tangential triangle is A"B"C", whose sides are the tangents to triangle ABC's circumcircle at its vertices; it is homothetic to the orthic triangle. The circumcenter of the tangential triangle, and the center of similitude of the orthic and tangential triangles, are on the Euler line.[20]:p. 447
Trilinear coordinates for the vertices of the tangential triangle are given by
- A" = −a : b : c
- B" = a : −b : c
- C" = a : b : −c.
For more information on the orthic triangle, see here.
3. Some Additional Altitude Theorems
3.1. Altitude in Terms of the Sides
For any triangle with sides a, b, c and semiperimeter s = (a + b + c) / 2, the altitude from side a is given by
- [math]\displaystyle{ h_a=\frac{2\sqrt{s(s-a)(s-b)(s-c)}}{a}. }[/math]
This follows from combining Heron's formula for the area of a triangle in terms of the sides with the area formula (1/2)×base×height, where the base is taken as side a and the height is the altitude from A.
3.2. Inradius Theorems
Consider an arbitrary triangle with sides a, b, c and with corresponding altitudes ha, hb, and hc. The altitudes and the incircle radius r are related by[29]:Lemma 1
- [math]\displaystyle{ \displaystyle \frac{1}{r}=\frac{1}{h_a}+\frac{1}{h_b}+\frac{1}{h_c}. }[/math]
3.3. Circumradius Theorem
Denoting the altitude from one side of a triangle as ha, the other two sides as b and c, and the triangle's circumradius (radius of the triangle's circumscribed circle) as R, the altitude is given by[30]
- [math]\displaystyle{ h_a=\frac{bc}{2R}. }[/math]
3.4. Interior Point
If p1, p2, and p3 are the perpendicular distances from any point P to the sides, and h1, h2, and h3 are the altitudes to the respective sides, then[31]
- [math]\displaystyle{ \frac{p_1}{h_1} +\frac{p_2}{h_2} + \frac{p_3}{h_3} = 1. }[/math]
3.5. Area Theorem
Denoting the altitudes of any triangle from sides a, b, and c respectively as [math]\displaystyle{ h_a }[/math], [math]\displaystyle{ h_b }[/math], and [math]\displaystyle{ h_c }[/math], and denoting the semi-sum of the reciprocals of the altitudes as [math]\displaystyle{ H = (h_a^{-1} + h_b^{-1} + h_c^{-1})/2 }[/math] we have[32]
- [math]\displaystyle{ \mathrm{Area}^{-1} = 4 \sqrt{H(H-h_a^{-1})(H-h_b^{-1})(H-h_c^{-1})}. }[/math]
3.6. General Point on an Altitude
If E is any point on an altitude AD of any triangle ABC, then[33]:77–78
- [math]\displaystyle{ AC^2+EB^2=AB^2+CE^2. }[/math]
3.7. Special Case Triangles
Equilateral triangle
For any point P within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle. This is Viviani's theorem.
Right triangle
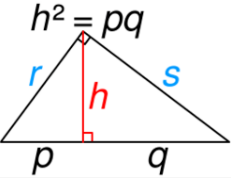
[math]\displaystyle{ \begin{align} (p + q)^2 \quad &= \quad\;\, r^2 \quad + \quad s^2 \\ p^2 \!+ 2pq + q^2 &= \left(h^2 \!\!+\! p^2\right) \!+\! \left(h^2 \!\!+\! q^2\right) \\ 2pq \qquad\, &= 2h^2 \quad \therefore h = \sqrt{pq} \\ \end{align} }[/math]
In a right triangle the three altitudes ha, hb, and hc (the first two of which equal the leg lengths b and a respectively) are related according to[34][35]
- [math]\displaystyle{ \frac{1}{h_a ^2}+\frac{1}{h_b ^2}=\frac{1}{h_c ^2}. }[/math]
4. History
The theorem that the three altitudes of a triangle meet in a single point, the orthocenter, was first proved in a 1749 publication by William Chapple.[36]
References
- Smart 1998, p. 156
- Berele & Goldman 2001, p. 118
- Clark Kimberling's Encyclopedia of Triangle Centers "Archived copy". Archived from the original on 2012-04-19. https://web.archive.org/web/20120419171900/http://faculty.evansville.edu/ck6/encyclopedia/ETC.html. Retrieved 2012-04-19.
- Andreescu, Titu; Andrica, Dorin, "Complex numbers from A to...Z". Birkhäuser, Boston, 2006, ISBN:978-0-8176-4326-3, page 90, Proposition 3
- Dörrie, Heinrich, "100 Great Problems of Elementary Mathematics. Their History and Solution". Dover Publications, Inc., New York, 1965, ISBN:0-486-61348-8, page 142
- Johnson 2007, p. 163, Section 255
- ""Orthocenter of a triangle"". http://www.pballew.net/orthocen.html.
- Johnson 2007, p. 176, Section 278
- Panapoi,Ronnachai, "Some properties of the orthocenter of a triangle", University of Georgia. http://jwilson.coe.uga.edu/EMAT6680Fa06/Panapoi/assignment_8/assignment8.htm
- Smart 1998, p. 182
- Weisstein, Eric W. "Isotomic conjugate" From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/IsotomicConjugate.html
- Weisstein, Eric W. "Orthocenter." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Orthocenter.html
- Altshiller-Court 2007, p. 102
- Bell, Amy, "Hansen's right triangle theorem, its converse and a generalization", Forum Geometricorum 6, 2006, 335–342. http://forumgeom.fau.edu/FG2006volume6/FG200639.pdf
- Weisstein, Eric W. "Kiepert Parabola." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/KiepertParabola.html
- Weisstein, Eric W. "Jerabek Hyperbola." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/JerabekHyperbola.html
- Berele & Goldman 2001, p. 123
- Berele & Goldman 2001, pp. 124-126
- Marie-Nicole Gras, "Distances between the circumcenter of the extouch triangle and the classical centers", Forum Geometricorum 14 (2014), 51-61. http://forumgeom.fau.edu/FG2014volume14/FG201405index.html
- Smith, Geoff, and Leversha, Gerry, "Euler and triangle geometry", Mathematical Gazette 91, November 2007, 436–452.
- William H. Barker, Roger Howe (2007). "§ VI.2: The classical coincidences". Continuous symmetry: from Euclid to Klein. American Mathematical Society. p. 292. ISBN 0-8218-3900-4. https://books.google.com/books?id=NIxExnr2EjYC&pg=PA292. See also: Corollary 5.5, p. 318.
- Johnson 2007, p. 199, Section 315
- Altshiller-Court 2007, p. 165
- Johnson 2007, p. 168, Section 264
- Berele & Goldman 2001, pp. 120-122
- Johnson 2007, p. 172, Section 270c
- Bryant, V., and Bradley, H., "Triangular Light Routes," Mathematical Gazette 82, July 1998, 298-299.
- Kay, David C. (1993), College Geometry / A Discovery Approach, HarperCollins, p. 6, ISBN 0-06-500006-4
- Dorin Andrica and Dan S ̧tefan Marinescu. "New Interpolation Inequalities to Euler’s R ≥ 2r". Forum Geometricorum, Volume 17 (2017), pp. 149–156. http://forumgeom.fau.edu/FG2017volume17/FG201719.pdf
- Johnson 2007, p. 71, Section 101a
- Johnson 2007, p. 74, Section 103c
- Mitchell, Douglas W., "A Heron-type formula for the reciprocal area of a triangle," Mathematical Gazette 89, November 2005, 494.
- Alfred S. Posamentier and Charles T. Salkind, Challenging Problems in Geometry, Dover Publishing Co., second revised edition, 1996.
- Voles, Roger, "Integer solutions of [math]\displaystyle{ a^{-2}+b^{-2}=d^{-2} }[/math]," Mathematical Gazette 83, July 1999, 269–271.
- Richinick, Jennifer, "The upside-down Pythagorean Theorem," Mathematical Gazette 92, July 2008, 313–317.
- Bogomolny, Alexander, "A Possibly First Proof of the Concurrence of Altitudes", Cut The Knot, https://www.cut-the-knot.org/triangle/Chapple.shtml, retrieved 2019-11-17




