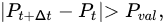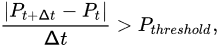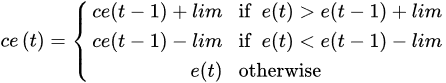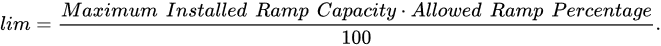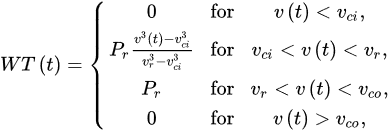1. Introduction
Renewable energy resources represent a valid alternative to the conventional power generation with the aim of increasing global welfare and decreasing pollution and global warming
[1]. The goal of reducing the emission of greenhouse gases is a current concern that has led to the necessity of using alternative energy sources to decrease the atmospheric pollution and all the issues related to it
[2][3][4]. Wind energy is one of the most-used renewable energy sources, but it is characterized by a variable and intermittent nature, which causes problems when connected to a grid, damaging its reliability and stability
[5]. Wind power tends to be unsteady because of the continuous wind speed fluctuations over time
[6]. The use of this renewable source has increased greatly in the last few decades. The installed capacity of wind power generation in the Electric Reliability Council of Texas (ERCOT) passed from 2 GW in 2006 to 16 GW in 2015
[7]. There are many variability-mitigating market rules for wind power production. Among them, it can be found the economic curtailment, curtailment to provide a power reserve, or using an energy storage system
[8]. In this perspective, the concept of the ramp rate limit is inserted. There is not a unique ramp rate definition in the literature
[9]. In general, a ramp event consists of a strong and rapid variation in power, and usually, it can be measured in MW/min or MW/hour. It represents the slope at which power changes, and it can be positive (ramp-up event where the power increases from one time step to the next one) or negative (ramp-down event where the power decreases)
[10][11]. When a ramp-up event is limited, the wind power plant produces less power compared to its possibility, and the difference can be stored in a storage system. Conversely, when a ramp-down event is limited, researchers need a greater amount of power to keep the power profile slope softer. In this case, an additional power source or storage system is strongly needed because they are controllable resources used to supply or store the energy required
[12]. The characteristics of the power storage system are also important because it has to provide a fast response to be able to supply or store the right amount of power in a short-term period. In the literature, the choice of a battery can be guided by different aspects, such as capacity, maximum power, life, operating temperature, cost, environmental impact, and efficiency
[13].
2. Ramp Rate Definition and Its Forecast
2.1. Ramp Rate Definition
Many studies attempt to give a definition of the ramp rate according to its duration, rate, and magnitude. Generally, the power ramp is a huge power change in a short time horizon
[14]. The researchers in
[15] consider a ramp rate event with an increase in wind power greater than
50% of the maximum capacity of the wind farm within a horizon time smaller than 4 h. In
[16], you can find the definition of the ramp event magnitude, which considers all the ramp events with an increase or decrease of power larger than
30% of the capacity of the wind farm as significant, and this is determined with the following equation:
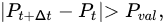
where
Pt is the wind power output at time
t,
Pt+Δt is the wind power output after a fixed time duration
Δt, and
Pval is a cut-off level (a threshold). Furthermore, the researchers in
[16] also considered the magnitude
Δt of the initial and final points of the time interval where the ramp change rate occurs and consider that a ramp event occurs when the ratio between the absolute value of the difference between the powers referring to two moments
Δt are farfrom each other and
Δt is greater than the threshold power value. This is shown in the following equation:
where
Pthreshold represents the maximum change rate power. For example, in
[17], there is the ramp rate when the change in power is greater than
50% of the wind plant capacity in an interval of time equal to 4 h. Here is the same equations in
[18].
As follows, it is possible to see the formula used in
[5] to modify the wind power output according to a chosen ramp rate limitation.
where e(t) is the limitless power output, ce(t) is the power output, which is modified according to a limitation, and lim represents the ramp rate limitation chosen, and it is equal to in wind power output with a rated capacity of 2 MW.
2.2. Forecasting of Wind Power Ramp Events
The stability of the grid operation is one of the most important issues caused by ramp events, and the harmful effects can be smoothed using different ramp forecasting methods. You can find an example of what can cause a rapid and huge drop of wind power that was not correctly predicted in the strong power imbalance event and the consequent cut out of almost
1.2 GW of power in Texas in 2008
[9][19].
These methods usually are composed by wind speed or wind power forecasts and ramp detection. In the first part, parametric and non-parametric are the two main methods used to model the wind power curve. The former uses linear or polynomial functions to fit the power curve; the latter needs historical data to create data mining algorithms to obtain a power curve similar to the one from the real data. It can be found physical models that use physical characteristics, such as meteorological or topological conditions, mathematical statistical models that consider the relation between historical wind power data and forecasting, such as neural networks and auto-regression and moving average (ARMA) models, and machine learning algorithms such as the artificial neural network (ANN), recurrent neural network (RNN), and extreme learning machine (ELM)
[20][21][22]. Recently, a non-parametric approach based on indexed semi-Markov processes proved to be efficient to predict wind power at different time scales
[23]. The ramp detection consists of two steps: the definition of the ramp and the implementation of algorithms to detect ramp events
[18][24].
The study performed in
[25] is interesting, where the researchers aimed to forecast the probability of exceeding a power threshold adapting the conditional autoregressive logit (CARL) model previously studied in
[26] to model the probability of wind power change overcoming a threshold. They used hourly wind power data of four wind farm on Crete (Greece), where the value of each hour is the average of six wind power readings recorded at the previous hour, and they considered six thresholds (
−0.3,
−0.2,
−0.1,
0.1,
0.2, and
0.3). They developed three new (CARL) models, namely conditional autoregressive multinomial logit (CARML) models. The first aims to estimate the probabilities of exceeding different thresholds by maximizing the likelihood of an expression based on a categorical distribution, which is a generalization of the Bernoulli distribution for a random variable with more than two possible outcomes. In the second one, they considered the spatial modeling using a bi-variate Bernoulli distribution to calculate the probability of a ramp rate event in different locations. With the last model, they estimated the model parameters for fours months, and they performed the probability forecast for the next month. They continued the procedure moving forward by one month. They were interested in forecasting from one to two steps ahead from the multi-step-ahead CARML model. The results show that both predictions are very promising compared to other models.
A different approach is proposed in
[24], where a hybrid forecasting model based on a semi-supervised generative adversarial network (GAN) was implemented to forecast wind power and ramp events. The GAN is a class of machine learning frameworks able to deduce the potential statistical distribution of the wind power time series. The merger of the semi-supervised regression with the GAN framework succeeds in decoding the nonlinear behaviors of the wind power data and improving the generated sample quality and decreasing the errors in the forecasting. More specifically, a signal decomposition techniques, variational mode decomposition, was used to divide wind power data into different sub-series with intrinsic mode functions that differ in frequency. Then, the GAN model was applied to generate virtual wind power data with the aim of finding the distribution characteristics of the wind power data. Finally, a GAN discriminative model was used to extract nonlinear features present in the data, and a semi-supervised regression was applied to predict the wind power for the next horizon time. The parameters of the GAN were updated through an alternative training process to minimize the errors of the predictions. The ramp event were divided into five categories according to the nature of the change (up or down event, small or large event, and no ramp event). The researchers compared this method with a classical neural network algorithm, deep learning algorithm, and statistical method, showing that it performs better according to different evaluation metrics (MAE, RMSE, and MAPE).
The researchers in
[27] considered wind data from three different wind farms in Hubei, which are characterized by different capacities. First of all, they used a swinging door algorithm (SDA) to identify the ramp segments. Then, they used a dynamic programming method to identify the ramp trend. Finally, they proposed a new improved dynamic swinging door algorithm (ImDSDA) with dynamic programming, which represents a combination of the SDA and sliding window (SW) algorithm and aims to solve the problem regarding the detection of ramp events and to obtain the optimal door width. This is a two-stage method characterized by high operability. The first stage contains the segment detection and classification. The second stage contains ramp event identification and segment combination. The results show that the this methodology improves the detection accuracy.
In
[18], a wind power prediction was obtained in two steps: wind power prediction and ramp detection. In this case, the non-parametric approach was used to build the prediction model and a Markov-switching auto-regression (MSAR) model was used to correct the prediction residual. The MSAR model represents a combination of AR models (which obtain the predictability of the data) and the Markov model (which obtain the randomness of the data thanks to the transition probability of the Markov chain), builds a residual correction model, and incorporates a random residual. At the end, an improved swinging door algorithm proposed in
[28] was used to see the linear segment thanks to it being possible to find the ramp event according to the ramp definitions. The researchers considered the 15 min wind data of a wind farm located in China. It was shown that this method performs better than the primary model and ARMA model.
A new statistical approach was proposed in
[16], where a practical metric based on real data was used to evaluate the forecasting performance of ramp events. The researchers calculated the hourly average of wind power and the ramp rate for each month and evaluated the seasonal standard ramp rate values as the input in the algorithm used to predict ramp events. Subsequently, the error metrics were used to evaluate the algorithm, such as BIAS, MAE, NMAE, and SDofAE.
It is also important to correctly choose the prediction time scale, called the time window in
[29], which can negatively influence the accuracy of predicting ramps. The researchers focused on optimizing the time window size in order to minimize non-ramp data in the chosen window, and the data analysis that they implemented consisted of extracting the ramp events, selecting the input variables and parameters, and solving the optimization problem through a genetic algorithm (GA) because of the nonlinearity of the objective function
[29].
The indirect method is more easily applicable because it does not require ramp rate data, as opposed to the direct method, which can only be applied by having already adhered to a ramp rate limitation policy. Nevertheless, researchers recommend implementing the ramp rate forecasting through an optimal mixture of the direct and indirect methods. However, this strategy needs real ramp event data, which are hardly available to researchers, but not to wind farm operators.
The different methods used depend strictly on the skills and means that researchers and practitioners have in their possession. The mathematical statistical methods generally need few resources to be applied as they are based on the analysis of the historical wind power series. Nevertheless, the required skills are advanced. This typology can be improved by adding information from physical methods in the form of covariates. The availability of information necessary to implement the physical methods could be limited to meteorological centers or to the installation of specific meteorological stations near the wind farm. Another relevant aspect in this regard is the time scale of the data provided. Finally, the availability of important computational resources could allow the support of machine learning methods frequently used in the last decade.
Increasing importance on ramp rate prediction has been placed in the literature because of the extreme rapidity of this type of event, which does not allow an adequate response of control systems. From this, researchers have the need of creating ever-more precise forecasting models, which represents the most effective way of dealing with ramp rate events
[30]. For this aspect, help could be given by creating a model that takes into account both the historical data available and the production data of already existing wind farms as close as possible to the area of interest. This could help to better understand the nature of the local wind speed.
3. Ramp Rate Limitation Control Strategies
3.1. Ramp Limitation Using a Battery Storage System
Many studies deal with the use of a battery storage system to limit and smooth the wind power fluctuation focusing on what type of battery and which size to choose. Obviously, the storage system should be as big as possible to maximize the smoothing of the ramp events. At the same time, the operator wants to minimize the cost, which means minimizing the capacity and the maximum power of the storage system. This is a trade-off that leads to finding the best combination between cost and storage characteristics through a multi-objective optimization approach
[31].
The inability to use the battery because it does not have enough space to store all the surplus of power or to supply the right quantity of power to comply with a ramp rate limitation could mean receiving a penalty
[5][8].
The battery (usually indicated with the acronym battery energy storage system (BESS)) is the most popular one due to the small area occupied for installation and its easy implementation. However, their application presents also some problems, such as the need to have a large capacity to cover the wind power fluctuations and the consequent increase of the capital and maintenance costs. In the field of wind power production, for this type of storage system, the most-used technologies are the lead-acid battery characterized by a low investment, easy installation, short lifetime, high maintenance, and poor performance at normal temperature, the nickel-based battery with a long lifetime, low maintenance, higher cost, and high self-discharge rate, and the sodium-sulfur battery with a high efficiency, good power density, high life cycle, considerable power density, thermal management, and low freeze–thaw durability
[32]. The important characteristics that a storage system should have for this kind of application are high energy efficiency and fast response
[32]. For example, in
[8], a NaS battery was used to implement different market policies such as ramp-up and ramp-down limitation. This choice is driven by the fact that this battery has a relatively established storage technology and a power-to-energy ratio suitable for ramp rate limitation. Furthermore, these batteries are modular and can be scaled based on the wind plant’s size. In the literature, several studies have investigated the best energy storage system to be coupled with a wind farm. In
[31], the researchers investigated the capacity of a battery storage system (BSS) to mitigate the ramp rate fluctuations depending on the storage capacity, the power rating, and the threshold chosen. In particular, they compared two different storage technologies and led a technical and economic analysis with a multi-objective optimization strategy to obtain the optimal balance between costs and abatement capacity in a realistic scenario considering maximum ramp rates equal to
5%,
7.5%, and
10%. The storage parameters, the power output from the wind turbine, and the maximum ramp rate represent the input of the model, and a black-box optimization problem was solved through a direct search algorithm implemented in MATLAB.
The minimum storage size to respect the ramp rate limitation was investigated in
[33] through an optimization problem implemented in Python and solved using Gurobi. Furthermore, Reference
[1] focused on the optimal energy storage system size problem for ramp rate control. This developed a novel representative day selection technique to select the days on which the optimal operation was based to elect the best size. The procedure was divided into two steps. In the first step, called pre-processing, the data were manipulated to be converted into a one-minute scale and sent to the second step (data clustering), where a set of representative days was chosen. To measure the performance of the selected days in the estimation of the battery size, a ramp rate violation penalty was applied.
Due to the direct proportionality between cost and capacity, it is fundamental to investigate control strategies that aim to optimize the operations of the BESS. Some examples of these methods are listed as follows
[32]:
-
Wind power filtering such as a low-pass filter, in which the higher elements of the frequency are blocked and the BESS has to store/supply the difference between the power value before and after the filter.
-
Charging/discharging dispatch, in which a control system manages the battery operations to obtain the required power to smooth the wind power production. In this context, researchers find the model predictive control framework.
-
Optimization with wind speed prediction, where the predictions are used to improve the control of the BESS.
A penalty can be charged to the wind farm for not respecting the ramp rate limitations
[8]. The recent study
[5] proposed a new method in which different ramp rate limitations were implemented in a hypothetical wind turbine connected to a battery located in Sardinia. The 10-year data of hourly wind speed were considered, and the battery must provide or supply the quantity of energy needed to comply with the limitation imposed. If the state-of-charge of the battery is not able to do this, the wind farm receives a penalty
[34]. The battery operations of charge and discharge are modeled as a discrete-time homogeneous Markov chain in which a state space composed by the following three states is considered:
+1for a charge event,
−1 for a discharge event, and 0 for the unchanged condition. The aim of the work is to simulate the state-of-charge over time and, consequently, calculate the amount of penalty that the wind farm receives during a given period.
This control strategy is the most used because of its fast response against rapid ramp events. Its applicability is directly connected with the design of increasingly better-performing and less-expensive batteries. Improving the ramp rate forecast can lead to the use of simpler and less-expensive storage system thanks to the possibility of setting the battery conditions (such as its state-of-charge) at the most appropriate state to best respond to the ramp event.
3.2. Ramp Limitation Using Physical Techniques
It is also important to remember that the power production of a wind turbine is regulated by a power curve. An example is proposed as follows
[5].
where
vco is the cut-out wind speed,
vci is the cut-in wind speed,
v(t) is the wind speed at time
t, and
vr and
Pr are the rated power and the rated wind speed. The wind power production strongly increases with the increase of wind speeds greater than
vci until
vco is reached and the turbine has a constant production (
Pr). In this way, four different areas can be defined in which the power production is differently ruled (in some studies, the researchers identify five areas
[35][36].
The use of a storage system is not the only approach to cope with the ramp rate of the wind power production
[37]. There are several ways to control a wind turbine. One way is represented by the generator torque control, where the controller fixes the generator torque in order to accelerate or decelerate the turbine with the aim of finding the optimal operation point while minimizing the loads
[35].
Other less-expensive control techniques consist of controlling the turbine blade pitch and the rotor inertia, but they require advanced control systems and are not suitable for quick responses
[38]. In the literature, these two methods of control are called active power control (APC) strategies, and they form two categories: the pitch-angle-regulation-based control (PAC) and the rotor-speed-regulation-based control (RSC)
[39]. The pitch control consists of adjusting the blades by rotating them in order to control the aerodynamic efficiency. In this way, it is guaranteed that the right fraction of the current wind power production is exploited and the maximum rotational speed is not overcome
[32]. Formerly, the turbines were controlled passively by means of the aerodynamic characteristics of the blades (an example is passive stall control), but this methodology was not very efficient. Modern wind turbines have active pitch control with electrical or hydraulic actuators
[35][40]. The second category consists of smoothing the wind power output by using the large inertia inherent in the wind rotor
[39][41][42]. In general, it is possible to have two types of wind turbine generators: constant-speed wind turbines and variable-speed wind turbines. The wind farm can control the frequency using inertia response methods and primary frequency response methods. The first one consists of using the wind farm droop controller and storing its rotational energy in the rotor, and this is possible by controlling the pitch angle
[43].
Most of these techniques act directly on the setting of the wind turbine and usually provide a slower response compared with the one provided by a storage system. It is the suggestion that, also in this case, the decision on which control strategy can be used depends on the characteristics of the wind and the ramp events that affect the location under study. For example, ramp events that last hours could be reasonably managed through physical techniques. Conversely, if the duration of the ramp events is of the order of minutes, it might be better to use a battery with a fast response.