1. Formulation

Data from two 3D scans of the same environment need to be aligned using point set registration.

Data from above, registered successfully using a variant of iterative closest point.

The problem may be summarized as follows:^[1] Let ${\displaystyle \{\mathcal{M},\mathcal{S}\}}$ be two finite size point sets in a finite-dimensional real vector space ${\displaystyle {\mathbb{R}}^d}$, which contain ${\displaystyle M}$ and ${\displaystyle N}$ points respectively (e.g., ${\displaystyle d=3}$ recovers the typical case of when ${\displaystyle \mathcal{M}}$ and ${\displaystyle \mathcal{S}}$ are 3D point sets). The problem is to find a transformation to be applied to the moving "model" point set ${\displaystyle \mathcal{M}}$ such that the difference (typically defined in the sense of point-wise Euclidean distance) between ${\displaystyle \mathcal{M}}$ and the static "scene" set ${\displaystyle \mathcal{S}}$ is minimized. In other words, a mapping from ${\displaystyle {\mathbb{R}}^d}$ to ${\displaystyle {\mathbb{R}}^d}$ is desired which yields the best alignment between the transformed "model" set and the "scene" set. The mapping may consist of a rigid or non-rigid transformation. The transformation model may be written as ${\displaystyle T}$, using which the transformed, registered model point set is:

${\displaystyle T(\mathcal{M})}$

(1)

The output of a point set registration algorithm is therefore the optimal transformation ${\displaystyle T^{\star }}$ such that ${\displaystyle \mathcal{M}}$ is best aligned to ${\displaystyle \mathcal{S}}$, according to some defined notion of distance function $\text{Undefined control sequence operatorname}$:

${\displaystyle T^{\star }=\arg \underset{T\in \mathcal{T}}{min}\text{dist}(T(\mathcal{M}),\mathcal{S})}$

(2)

where ${\displaystyle \mathcal{T}}$ is used to denote the set of all possible transformations that the optimization tries to search for. The most popular choice of the distance function is to take the square of the Euclidean distance for every pair of points:

$\text{Undefined control sequence operatorname}$

(3)

where ${\displaystyle \Vert \cdot {\Vert }_2}$ denotes the vector 2-norm, ${\displaystyle s_m}$ is the corresponding point in set ${\displaystyle \mathcal{S}}$ that attains the shortest distance to a given point ${\displaystyle m}$ in set ${\displaystyle \mathcal{M}}$ after transformation. Minimizing such a function in rigid registration is equivalent to solving a least squares problem.

2. Types of Algorithms

When the correspondences (i.e., ${\displaystyle s_m\leftrightarrow m}$) are given before the optimization, for example, using feature matching techniques, then the optimization only needs to estimate the transformation. This type of registration is called correspondence-based registration. On the other hand, if the correspondences are unknown, then the optimization is required to jointly find out the correspondences and transformation together. This type of registration is called simultaneous pose and correspondence registration.

2.1. Rigid Registration

Given two point sets, rigid registration yields a rigid transformation which maps one point set to the other. A rigid transformation is defined as a transformation that does not change the distance between any two points. Typically such a transformation consists of translation and rotation.^[2] In rare cases, the point set may also be mirrored. In robotics and computer vision, rigid registration has the most applications.

2.2. Non-Rigid Registration

Registered point cloud from a lidar mounted on a moving car.

Given two point sets, non-rigid registration yields a non-rigid transformation which maps one point set to the other. Non-rigid transformations include affine transformations such as scaling and shear mapping. However, in the context of point set registration, non-rigid registration typically involves nonlinear transformation. If the eigenmodes of variation of the point set are known, the nonlinear transformation may be parametrized by the eigenvalues.^[3] A nonlinear transformation may also be parametrized as a thin plate spline.^[3][4]

2.3. Other Types

Some approaches to point set registration use algorithms that solve the more general graph matching problem.^[1] However, the computational complexity of such methods tend to be high and they are limited to rigid registrations. In this article, we will only consider algorithms for rigid registration, where the transformation is assumed to contain 3D rotations and translations (possibly also including a uniform scaling).

The PCL (Point Cloud Library) is an open-source framework for n-dimensional point cloud and 3D geometry processing. It includes several point registration algorithms.^[5]

3. Correspondence-based Registration

Correspondence-based methods assume the putative correspondences ${\displaystyle m\leftrightarrow s_m}$ are given for every point ${\displaystyle m\in \mathcal{M}}$. Therefore, we arrive at a setting where both point sets ${\displaystyle \mathcal{M}}$ and ${\displaystyle \mathcal{S}}$ have ${\displaystyle N}$ points and the correspondences ${\displaystyle m_i\leftrightarrow s_i,i=1,\dots ,N}$are given.

3.1. Outlier-Free Registration

In the simplest case, one can assume that all the correspondences are correct, meaning that the points ${\displaystyle m_i,s_i\in {\mathbb{R}}^3}$ are generated as follows:

${\displaystyle s_i=lR{m}_i+t+{ϵ}_i,i=1,\dots ,N}$

(cb.1)

where ${\displaystyle l>0}$ is a uniform scaling factor (in many cases ${\displaystyle l=1}$ is assumed), ${\displaystyle R\in \text{SO}(3)}$ is a proper 3D rotation matrix (${\displaystyle \text{SO}(d)}$ is the special orthogonal group of degree ${\displaystyle d}$), ${\displaystyle t\in {\mathbb{R}}^3}$ is a 3D translation vector and ${\displaystyle {ϵ}_i\in {\mathbb{R}}^3}$ models the unknown additive noise (e.g., Gaussian noise). Specifically, if the noise ${\displaystyle {ϵ}_i}$ is assumed to follow a zero-mean isotropic Gaussian distribution with standard deviation ${\displaystyle {\sigma }_i}$, i.e., ${\displaystyle {ϵ}_i\sim \mathcal{N}(0,{\sigma }_i^2{I}_3)}$, then the following optimization can be shown to yield the maximum likelihood estimate for the unknown scale, rotation and translation:

${\displaystyle l^{\star },R^{\star },t^{\star }=\arg \underset{l>0,R\in \text{SO}(3),t\in {\mathbb{R}}^3}{min}\sum _{i=1}^N\frac{1}{{\sigma }_i^2}{\Vert s_i-lR{m}_i-t\Vert }_2^2}$

(cb.2)

Note that when the scaling factor is 1 and the translation vector is zero, then the optimization recovers the formulation of the Wahba problem. Despite the non-convexity of the optimization (cb.2) due to non-convexity of the set ${\displaystyle \text{SO}(3)}$, seminal work by Berthold K.P. Horn showed that (cb.2) actually admits a closed-form solution, by decoupling the estimation of scale, rotation and translation.^[6] Similar results were discovered by Arun et al.^[7] In addition, in order to find a unique transformation ${\displaystyle (l,R,t)}$, at least ${\displaystyle N=3}$ non-collinear points in each point set are required.

More recently, Briales and Gonzalez-Jimenez have developed a semidefinite relaxation using Lagrangian duality, for the case where the model set ${\displaystyle \mathcal{M}}$ contains different 3D primitives such as points, lines and planes (which is the case when the model ${\displaystyle \mathcal{M}}$ is a 3D mesh).^[8] Interestingly, the semidefinite relaxation is empirically tight, i.e., a certifiably globally optimal solution can be extracted from the solution of the semidefinite relaxation.

3.2. Robust Registration

The least squares formulation (cb.2) is known to perform arbitrarily bad in the presence of outliers. An outlier correspondence is a pair of measurements ${\displaystyle s_i\leftrightarrow m_i}$ that departs from the generative model (cb.1). In this case, one can consider a different generative model as follows:^[9]

$\text{Unknown environment 'cases'}$

(cb.3)

where if the ${\displaystyle i-}$th pair ${\displaystyle s_i\leftrightarrow m_i}$ is an inlier, then it obeys the outlier-free model (cb.1), i.e., ${\displaystyle s_i}$ is obtained from ${\displaystyle m_i}$ by a spatial transformation plus some small noise; however, if the ${\displaystyle i-}$th pair ${\displaystyle s_i\leftrightarrow m_i}$ is an outlier, then ${\displaystyle s_i}$ can be any arbitrary vector ${\displaystyle o_i}$. Since one does not know which correspondences are outliers beforehand, robust registration under the generative model (cb.3) is of paramount importance for computer vision and robotics deployed in the real world, because current feature matching techniques tend to output highly corrupted correspondences where over ${\displaystyle 95\mathrm{\%}}$ of the correspondences can be outliers.^[10]

Next, we describe several common paradigms for robust registration.

Maximum consensus

Maximum consensus seeks to find the largest set of correspondences that are consistent with the generative model (cb.1) for some choice of spatial transformation ${\displaystyle (l,R,t)}$. Formally speaking, maximum consensus solves the following optimization:

${\displaystyle \underset{l>0,R\in \text{SO}(3),t\in {\mathbb{R}}^3,\mathcal{I}}{max}|\mathcal{I}|,\text{subject to }\frac{1}{{\sigma }_i^2}\Vert s_i-lR{m}_i-t{\Vert }_2^2\le \xi ,\mathrm{\forall }i\in \mathcal{I}}$

(cb.4)

where ${\displaystyle |\mathcal{I}|}$ denotes the cardinality of the set ${\displaystyle \mathcal{I}}$. The constraint in (cb.4) enforces that every pair of measurements in the inlier set ${\displaystyle \mathcal{I}}$ must have residuals smaller than a pre-defined threshold ${\displaystyle \xi }$. Unfortunately, recent analyses have shown that globally solving problem (cb.4) is NP-Hard, and global algorithms typically have to resort to branch-and-bound (BnB) techniques that take exponential-time complexity in the worst case.^{[11][12][13][14][15]}

Although solving consensus maximization exactly is hard, there exist efficient heuristics that perform quite well in practice. One of the most popular heuristics is the Random Sample Consensus (RANSAC) scheme.^[16] RANSAC is an iterative hypothesize-and-verity method. At each iteration, the method first randomly samples 3 out of the total number of ${\displaystyle N}$ correspondences and computes a hypothesis ${\displaystyle (l,R,t)}$ using Horn's method,^[6] then the method evaluates the constraints in (cb.4) to count how many correspondences actually agree with such a hypothesis (i.e., it computes the residual ${\displaystyle \Vert s_i-lR{m}_i-t{\Vert }_2^2/{\sigma }_i^2}$ and compares it with the threshold ${\displaystyle \xi }$ for each pair of measurements). The algorithm terminates either after it has found a consensus set that has enough correspondences, or after it has reached the total number of allowed iterations. RANSAC is highly efficient because the main computation of each iteration is carrying out the closed-form solution in Horn's method. However, RANSAC is non-deterministic and only works well in the low-outlier-ratio regime (e.g., below ${\displaystyle 50\mathrm{\%}}$), because its runtime grows exponentially with respect to the outlier ratio.^[10]

To fill the gap between the fast but inexact RANSAC scheme and the exact but exhaustive BnB optimization, recent researches have developed deterministic approximate methods to solve consensus maximization.^{[11][12][13][17]}

Outlier removal

Outlier removal methods seek to pre-process the set of highly corrupted correspondences before estimating the spatial transformation. The motivation of outlier removal is to significantly reduce the number of outlier correspondences, while maintaining inlier correspondences, so that optimization over the transformation becomes easier and more efficient (e.g., RANSAC works poorly when the outlier ratio is above ${\displaystyle 95\mathrm{\%}}$ but performs quite well when outlier ratio is below ${\displaystyle 50\mathrm{\%}}$).

Parra et al. have proposed a method called Guaranteed Outlier Removal (GORE) that uses geometric constraints to prune outlier correspondences while guaranteeing to preserve inlier correspondences.^[10] GORE has been shown to be able to drastically reduce the outlier ratio, which can significantly boost the performance of consensus maximization using RANSAC or BnB. Yang and Carlone have proposed to build pairwise translation-and-rotation-invariant measurements (TRIMs) from the original set of measurements and embed TRIMs as the edges of a graph whose nodes are the 3D points. Since inliers are pairwise consistent in terms of the scale, they must form a clique within the graph. Therefore, using efficient algorithms for computing the maximum clique of a graph can find the inliers and effectively prune the outliers.^[18] The maximum clique based outlier removal method is also shown to be quite useful in real-world point set registration problems.^[9] Similar outlier removal ideas were also proposed by Parra et al..^[19]

M-estimation

M-estimation replaces the least squares objective function in (cb.2) with a robust cost function that is less sensitive to outliers. Formally, M-estimation seeks to solve the following problem:

${\displaystyle l^{\star },R^{\star },t^{\star }=\arg \underset{l>0,R\in \text{SO}(3),t\in {\mathbb{R}}^3}{min}\sum _{i=1}^N\rho \left(\frac{1}{{\sigma }_i}{\Vert s_i-lR{m}_i-t\Vert }_2\right)}$

(cb.5)

where ${\displaystyle \rho (\cdot )}$ represents the choice of the robust cost function. Note that choosing ${\displaystyle \rho (x)=x^2}$ recovers the least squares estimation in (cb.2). Popular robust cost functions include ${\displaystyle {\ell }_1}$-norm loss, Huber loss,^[20] Geman-McClure loss^[21] and truncated least squares loss.^[9][18][22] M-estimation has been one of the most popular paradigms for robust estimation in robotics and computer vision.^[23][24] Because robust objective functions are typically non-convex (e.g., the truncated least squares loss v.s. the least squares loss), algorithms for solving the non-convex M-estimation are typically based on local optimization, where first an initial guess is provided, following by iterative refinements of the transformation to keep decreasing the objective function. Local optimization tends to work well when the initial guess is close to the global minimum, but it is also prone to get stuck in local minima if provided with poor initialization.

Graduated non-convexity

Graduated non-convexity (GNC) is a general-purpose framework for solving non-convex optimization problems without initialization. It has achieved success in early vision and machine learning applications.^[25][26] The key idea behind GNC is to solve the hard non-convex problem by starting from an easy convex problem. Specifically, for a given robust cost function ${\displaystyle \rho (\cdot )}$, one can construct a surrogate function ${\displaystyle {\rho }_{\mu }(\cdot )}$ with a hyper-parameter ${\displaystyle \mu }$, tuning which can gradually increase the non-convexity of the surrogate function ${\displaystyle {\rho }_{\mu }(\cdot )}$ until it converges to the target function ${\displaystyle \rho (\cdot )}$.^[26][27] Therefore, at each level of the hyper-parameter ${\displaystyle \mu }$, the following optimization is solved:

${\displaystyle l_{\mu }^{\star },R_{\mu }^{\star },t_{\mu }^{\star }=\arg \underset{l>0,R\in \text{SO}(3),t\in {\mathbb{R}}^3}{min}\sum _{i=1}^N{\rho }_{\mu }\left(\frac{1}{{\sigma }_i}{\Vert s_i-lR{m}_i-t\Vert }_2\right)}$

(cb.6)

Black and Rangarajan proved that the objective function of each optimization (cb.6) can be dualized into a sum of weighted least squares and a so-called outlier process function on the weights that determine the confidence of the optimization in each pair of measurements.^[25] Using Black-Rangarajan duality and GNC tailored for the Geman-McClure function, Zhou et al. developed the fast global registration algorithm that is robust against about ${\displaystyle 80\mathrm{\%}}$ outliers in the correspondences.^[21] More recently, Yang et al. showed that the joint use of GNC (tailored to the Geman-McClure function and the truncated least squares function) and Black-Rangarajan duality can lead to a general-purpose solver for robust registration problems, including point clouds and mesh registration.^[27]

Certifiably robust registration

Almost none of the robust registration algorithms mentioned above (except the BnB algorithm that runs in exponential-time in the worst case) comes with performance guarantees, which means that these algorithms can return completely incorrect estimates without notice. Therefore, these algorithms are undesirable for safety-critical applications like autonomous driving.

Very recently, Yang et al. has developed the first certifiably robust registration algorithm, named Truncated least squares Estimation And SEmidefinite Relaxation (TEASER).^[9] For point cloud registration, TEASER not only outputs an estimate of the transformation, but also quantifies the optimality of the given estimate. TEASER adopts the following truncated least squares (TLS) estimator:

${\displaystyle l^{\star },R^{\star },t^{\star }=\arg \underset{l>0,R\in \text{SO}(3),t\in {\mathbb{R}}^3}{min}\sum _{i=1}^{N}min(\frac{1}{{\sigma }_i^2}{\Vert s_i-lR{m}_i-t\Vert }_2^2,{\overline{c}}^2)}$

(cb.7)

which is obtained by choosing the TLS robust cost function ${\displaystyle \rho (x)=min(x^2,{\overline{c}}^2)}$, where ${\displaystyle {\overline{c}}^2}$is a pre-defined constant that determines the maximum allowed residuals to be considered inliers. The TLS objective function has the property that for inlier correspondences (${\displaystyle \Vert s_i-lR{m}_i-t{\Vert }_2^2/{\sigma }_i^2<{\overline{c}}^2}$), the usual least square penalty is applied; while for outlier correspondences (${\displaystyle \Vert s_i-lR{m}_i-t{\Vert }_2^2/{\sigma }_i^2>{\overline{c}}^2}$), no penalty is applied and the outliers are discarded. If the TLS optimization (cb.7) is solved to global optimality, then it is equivalent to running Horn's method on only the inlier correspondences.

However, solving (cb.7) is quite challenging due to its combinatorial nature. TEASER solves (cb.7) as follows : (i) It builds invariant measurements such that the estimation of scale, rotation and translation can be decoupled and solved separately, a strategy that is inspired by the original Horn's method; (ii) The same TLS estimation is applied for each of the three sub-problems, where the scale TLS problem can be solved exactly using an algorithm called adaptive voting, the rotation TLS problem can relaxed to a semidefinite program (SDP) where the relaxation is exact in practice,^[22] even with large amount of outliers; the translation TLS problem can solved using component-wise adaptive voting. A fast implementation leveraging GNC is open-sourced here. In practice, TEASER can tolerate more than ${\displaystyle 99\mathrm{\%}}$ outlier correspondences and runs in milliseconds.

In addition to developing TEASER, Yang et al. also prove that, under some mild conditions on the point cloud data, TEASER's estimated transformation has bounded errors from the ground-truth transformation.^[9]

4. Simultaneous Pose and Correspondence Registration

4.1. Iterative Closest Point

The iterative closest point (ICP) algorithm was introduced by Besl and McKay.^[28] The algorithm performs rigid registration in an iterative fashion by alternating in (i) given the transformation, finding the closest point in ${\displaystyle \mathcal{S}}$ for every point in ${\displaystyle \mathcal{M}}$; and (ii) given the correspondences, finding the best rigid transformation by solving the least squares problem (cb.2). As such, it works best if the initial pose of ${\displaystyle \mathcal{M}}$ is sufficiently close to ${\displaystyle \mathcal{S}}$. In pseudocode, the basic algorithm is implemented as follows:

algorithm ICP(M, S) θ := θ0 while not registered: X := ∅ for mi ∊ T(M, θ): ŝj := closest point in S to mi X := X + ⟨mi, ŝj⟩ θ := least_squares(X) return θ 

Here, the function least_squares performs least squares optimization to minimize the distance in each of the ${\displaystyle ⟨m_i,{\hat{s}}_j⟩}$ pairs, using the closed-form solutions by Horn^[6] and Arun.^[7]

Because the cost function of registration depends on finding the closest point in ${\displaystyle \mathcal{S}}$ to every point in ${\displaystyle \mathcal{M}}$, it can change as the algorithm is running. As such, it is difficult to prove that ICP will in fact converge exactly to the local optimum.^[29] In fact, empirically, ICP and EM-ICP do not converge to the local minimum of the cost function.^[29] Nonetheless, because ICP is intuitive to understand and straightforward to implement, it remains the most commonly used point set registration algorithm.^[29] Many variants of ICP have been proposed, affecting all phases of the algorithm from the selection and matching of points to the minimization strategy.^[3][30] For example, the expectation maximization algorithm is applied to the ICP algorithm to form the EM-ICP method, and the Levenberg-Marquardt algorithm is applied to the ICP algorithm to form the LM-ICP method.^[2]

4.2. Robust Point Matching

Robust point matching (RPM) was introduced by Gold et al.^[31] The method performs registration using deterministic annealing and soft assignment of correspondences between point sets. Whereas in ICP the correspondence generated by the nearest-neighbour heuristic is binary, RPM uses a soft correspondence where the correspondence between any two points can be anywhere from 0 to 1, although it ultimately converges to either 0 or 1. The correspondences found in RPM is always one-to-one, which is not always the case in ICP.^[4] Let ${\displaystyle m_i}$ be the ${\displaystyle i}$th point in ${\displaystyle \mathcal{M}}$ and ${\displaystyle s_j}$ be the ${\displaystyle j}$th point in ${\displaystyle \mathcal{S}}$. The match matrix ${\displaystyle \mu }$ is defined as such:

$\text{Unknown environment 'cases'}$

(rpm.1)

The problem is then defined as: Given two point sets ${\displaystyle \mathcal{M}}$ and ${\displaystyle \mathcal{S}}$ find the Affine transformation ${\displaystyle T}$ and the match matrix ${\displaystyle \mu }$ that best relates them.^[31] Knowing the optimal transformation makes it easy to determine the match matrix, and vice versa. However, the RPM algorithm determines both simultaneously. The transformation may be decomposed into a translation vector and a transformation matrix:

${\displaystyle T(m)=\mathbf{A}m+\mathbf{t}}$

The matrix ${\displaystyle \mathbf{A}}$ in 2D is composed of four separate parameters ${\displaystyle \{a,\theta ,b,c\}}$, which are scale, rotation, and the vertical and horizontal shear components respectively. The cost function is then:

$\text{Undefined control sequence operatorname}$

(rpm.2)

subject to ${\displaystyle \mathrm{\forall }j\sum _{i=1}^M{\mu }_{ij}\le 1}$, ${\displaystyle \mathrm{\forall }i\sum _{j=1}^N{\mu }_{ij}\le 1}$, ${\displaystyle \mathrm{\forall }ij{\mu }_{ij}\in \{0,1\}}$. The ${\displaystyle \alpha }$ term biases the objective towards stronger correlation by decreasing the cost if the match matrix has more ones in it. The function ${\displaystyle g(\mathbf{A})}$ serves to regularize the Affine transformation by penalizing large values of the scale and shear components:

${\displaystyle g(\mathbf{A}(a,\theta ,b,c))=\gamma (a^2+b^2+c^2)}$

for some regularization parameter ${\displaystyle \gamma }$.

The RPM method optimizes the cost function using the Softassign algorithm. The 1D case will be derived here. Given a set of variables ${\displaystyle \{Q_j\}}$ where ${\displaystyle Q_j\in {\mathbb{R}}^1}$. A variable ${\displaystyle {\mu }_j}$ is associated with each ${\displaystyle Q_j}$ such that ${\displaystyle \sum _{j=1}^J{\mu }_j=1}$. The goal is to find ${\displaystyle \mu }$ that maximizes ${\displaystyle \sum _{j=1}^J{\mu }_j{Q}_j}$. This can be formulated as a continuous problem by introducing a control parameter ${\displaystyle \beta >0}$. In the deterministic annealing method, the control parameter ${\displaystyle \beta }$ is slowly increased as the algorithm runs. Let ${\displaystyle \mu }$ be:

${\displaystyle {\mu }_{\hat{j}}=\frac{\exp (\beta Q_{\hat{j}})}{\sum _{j=1}^J\exp (\beta Q_j)}}$

(rpm.3)

this is known as the softmax function. As ${\displaystyle \beta }$ increases, it approaches a binary value as desired in Equation (rpm.1). The problem may now be generalized to the 2D case, where instead of maximizing ${\displaystyle \sum _{j=1}^J{\mu }_j{Q}_j}$, the following is maximized:

${\displaystyle E(\mu )=\sum _{j=1}^N\sum _{i=0}^M{\mu }_{ij}{Q}_{ij}}$

(rpm.4)

where

$\text{Undefined control sequence lVert}$

This is straightforward, except that now the constraints on ${\displaystyle \mu }$ are doubly stochastic matrix constraints: ${\displaystyle \mathrm{\forall }j\sum _{i=1}^M{\mu }_{ij}=1}$ and ${\displaystyle \mathrm{\forall }i\sum _{j=1}^N{\mu }_{ij}=1}$. As such the denominator from Equation (rpm.3) cannot be expressed for the 2D case simply. To satisfy the constraints, it is possible to use a result due to Sinkhorn,^[31] which states that a doubly stochastic matrix is obtained from any square matrix with all positive entries by the iterative process of alternating row and column normalizations. Thus the algorithm is written as such:^[31]

algorithm RPM2D[math]\displaystyle{ (\mathcal{M}, \mathcal{S}) }[/math] t := 0 a, θ b, c := 0 β := β0 [math]\displaystyle{ \hat{\mu}_{ij} := 1 + \epsilon }[/math] while β < βf: while μ has not converged: // update correspondence parameters by softassign [math]\displaystyle{ Q_{ij} := -\frac{\partial \operatorname{cost}}{\partial \mu_{ij}} }[/math] [math]\displaystyle{ \mu^0_{ij} := \exp(\beta Q_{ij}) }[/math] // apply Sinkhorn's method while [math]\displaystyle{ \hat{\mu} }[/math] has not converged: // update [math]\displaystyle{ \hat{\mu} }[/math] by normalizing across all rows: [math]\displaystyle{ \hat{\mu}^1_{ij} := \frac{\hat{\mu}^0_{ij}}{\sum_{i=1}^{M+1} \hat{\mu}^0_{ij}} }[/math] // update [math]\displaystyle{ \hat{\mu} }[/math] by normalizing across all columns: [math]\displaystyle{ \hat{\mu}^0_{ij} := \frac{\hat{\mu}^1_{ij}}{\sum_{j=1}^{N+1} \hat{\mu}^1_{ij}} }[/math] // update pose parameters by coordinate descent update θ using analytical solution update t using analytical solution update a, b, c using Newton's method [math]\displaystyle{ \beta := \beta_r \beta }[/math] [math]\displaystyle{ \gamma := \frac{\gamma}{\beta_r} }[/math] return a, b, c, θ and t 

where the deterministic annealing control parameter ${\displaystyle \beta }$ is initially set to ${\displaystyle {\beta }_0}$ and increases by factor ${\displaystyle {\beta }_r}$ until it reaches the maximum value ${\displaystyle {\beta }_f}$. The summations in the normalization steps sum to ${\displaystyle M+1}$ and ${\displaystyle N+1}$ instead of just ${\displaystyle M}$ and ${\displaystyle N}$ because the constraints on ${\displaystyle \mu }$ are inequalities. As such the ${\displaystyle M+1}$th and ${\displaystyle N+1}$th elements are slack variables.

The algorithm can also be extended for point sets in 3D or higher dimensions. The constraints on the correspondence matrix ${\displaystyle \mu }$ are the same in the 3D case as in the 2D case. Hence the structure of the algorithm remains unchanged, with the main difference being how the rotation and translation matrices are solved.^[31]

Thin plate spline robust point matching

Animation of 2D non-rigid registration of the green point set ${\displaystyle \mathcal{M}}$ to the magenta point set ${\displaystyle \mathcal{S}}$ corrupted with noisy outliers. The size of the blue circles is inversely related to the control parameter ${\displaystyle \beta }$. The yellow lines indicate correspondence.

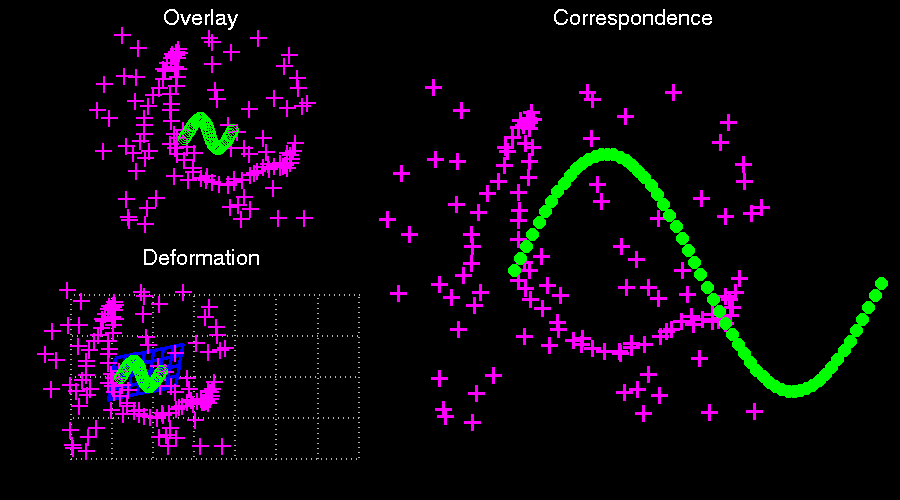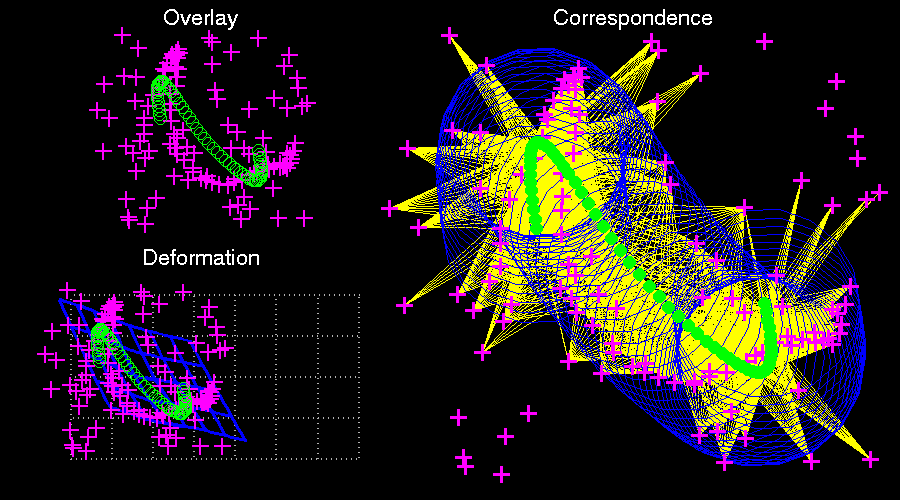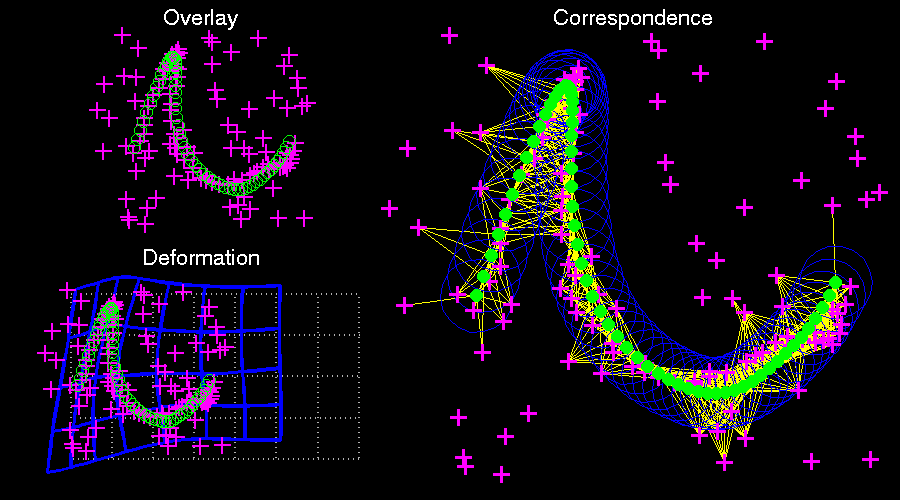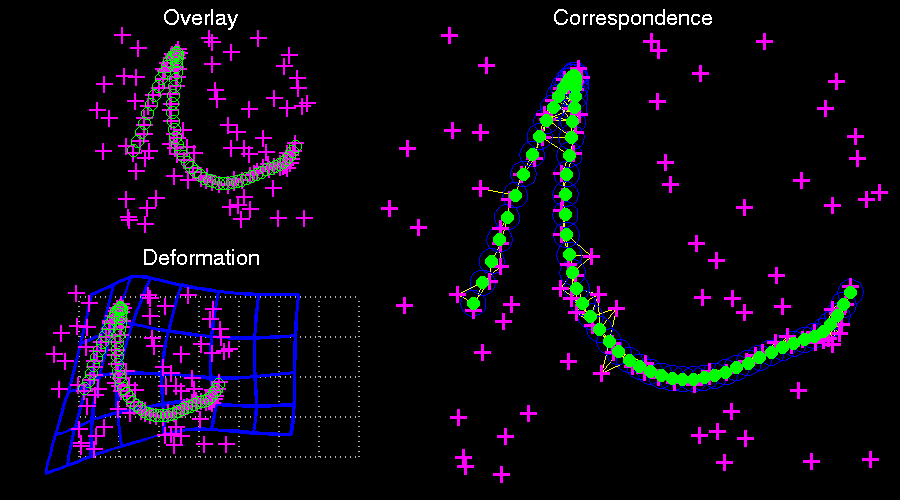
The thin plate spline robust point matching (TPS-RPM) algorithm by Chui and Rangarajan augments the RPM method to perform non-rigid registration by parametrizing the transformation as a thin plate spline.^[4] However, because the thin plate spline parametrization only exists in three dimensions, the method cannot be extended to problems involving four or more dimensions.

4.3. Kernel Correlation

The kernel correlation (KC) approach of point set registration was introduced by Tsin and Kanade.^[29] Compared with ICP, the KC algorithm is more robust against noisy data. Unlike ICP, where, for every model point, only the closest scene point is considered, here every scene point affects every model point.^[29] As such this is a multiply-linked registration algorithm. For some kernel function ${\displaystyle K}$, the kernel correlation ${\displaystyle KC}$ of two points ${\displaystyle x_i,x_j}$ is defined thus:^[29]

${\displaystyle KC(x_i,x_j)=\int K(x,x_i)\cdot K(x,x_j)dx}$

(kc.1)

The kernel function ${\displaystyle K}$ chosen for point set registration is typically symmetric and non-negative kernel, similar to the ones used in the Parzen window density estimation. The Gaussian kernel typically used for its simplicity, although other ones like the Epanechnikov kernel and the tricube kernel may be substituted.^[29] The kernel correlation of an entire point set ${\displaystyle \chi }$ is defined as the sum of the kernel correlations of every point in the set to every other point in the set:^[29]

${\displaystyle KC(\mathcal{X})=\sum _{i\ne j}KC(x_i,x_j)=2\sum _{i<j}KC(x_i,x_j)}$

(kc.2)

The logarithm of KC of a point set is proportional, within a constant factor, to the information entropy. Observe that the KC is a measure of a "compactness" of the point set—trivially, if all points in the point set were at the same location, the KC would evaluate to a large value. The cost function of the point set registration algorithm for some transformation parameter ${\displaystyle \theta }$ is defined thus:

$\text{Undefined control sequence operatorname}$

(kc.3)

Some algebraic manipulation yields:

$\text{Undefined control sequence operatorname}$

(kc.4)

The expression is simplified by observing that ${\displaystyle KC(\mathcal{S})}$ is independent of ${\displaystyle \theta }$. Furthermore, assuming rigid registration, ${\displaystyle KC(T(\mathcal{M},\theta ))}$ is invariant when ${\displaystyle \theta }$ is changed because the Euclidean distance between every pair of points stays the same under rigid transformation. So the above equation may be rewritten as:

$\text{Undefined control sequence operatorname}$

(kc.5)

The kernel density estimates are defined as:

${\displaystyle P_{\mathcal{M}}(x,\theta )=\frac{1}{M}\sum _{m\in \mathcal{M}}K(x,T(m,\theta ))}$

${\displaystyle P_{\mathcal{S}}(x)=\frac{1}{N}\sum _{s\in \mathcal{S}}K(x,s)}$

The cost function can then be shown to be the correlation of the two kernel density estimates:

$\text{Undefined control sequence operatorname}$

(kc.6)

Having established the cost function, the algorithm simply uses gradient descent to find the optimal transformation. It is computationally expensive to compute the cost function from scratch on every iteration, so a discrete version of the cost function Equation (kc.6) is used. The kernel density estimates ${\displaystyle P_{\mathcal{M}},P_{\mathcal{S}}}$ can be evaluated at grid points and stored in a lookup table. Unlike the ICP and related methods, it is not necessary to find the nearest neighbour, which allows the KC algorithm to be comparatively simple in implementation.

Compared to ICP and EM-ICP for noisy 2D and 3D point sets, the KC algorithm is less sensitive to noise and results in correct registration more often.^[29]

Gaussian mixture model

The kernel density estimates are sums of Gaussians and may therefore be represented as Gaussian mixture models (GMM).^[32] Jian and Vemuri use the GMM version of the KC registration algorithm to perform non-rigid registration parametrized by thin plate splines.

4.4. Coherent Point Drift

Rigid (with the addition of scaling) registration of a blue point set ${\displaystyle \mathcal{M}}$ to the red point set ${\displaystyle \mathcal{S}}$ using the Coherent Point Drift algorithm. Both point sets have been corrupted with removed points and random spurious outlier points.

Affine registration of a blue point set ${\displaystyle \mathcal{M}}$ to the red point set ${\displaystyle \mathcal{S}}$ using the Coherent Point Drift algorithm.

Non-rigid registration of a blue point set ${\displaystyle \mathcal{M}}$ to the red point set ${\displaystyle \mathcal{S}}$ using the Coherent Point Drift algorithm. Both point sets have been corrupted with removed points and random spurious outlier points.

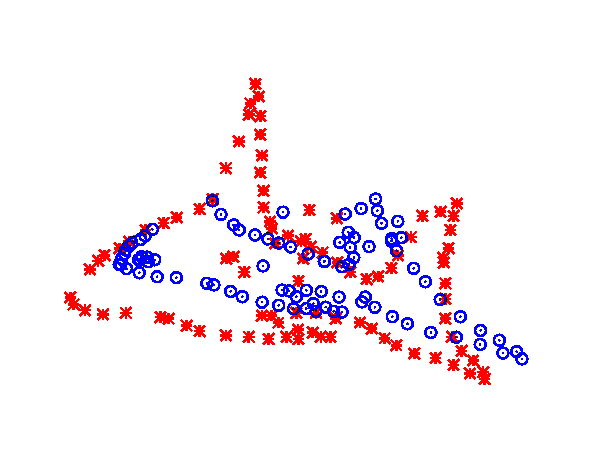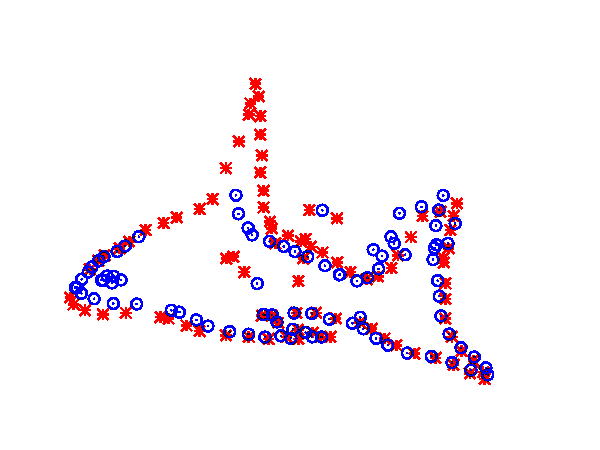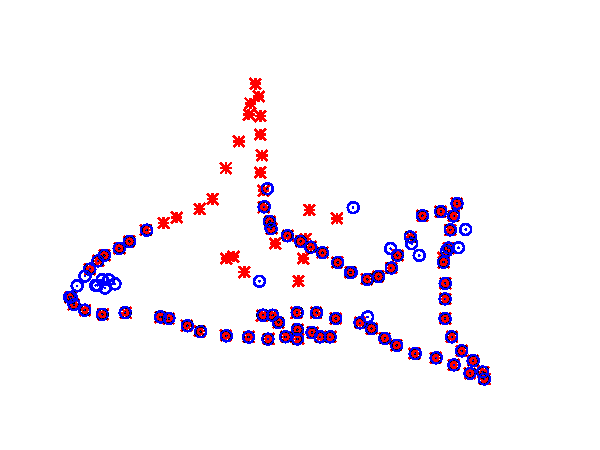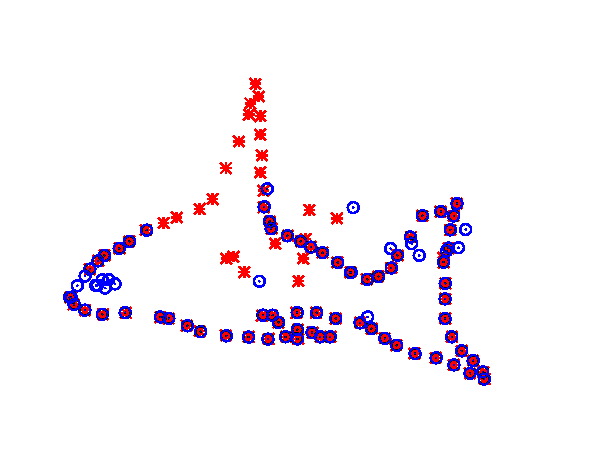
Coherent point drift (CPD) was introduced by Myronenko and Song.^[3][33] The algorithm takes a probabilistic approach to aligning point sets, similar to the GMM KC method. Unlike earlier approaches to non-rigid registration which assume a thin plate spline transformation model, CPD is agnostic with regard to the transformation model used. The point set ${\displaystyle \mathcal{M}}$ represents the Gaussian mixture model (GMM) centroids. When the two point sets are optimally aligned, the correspondence is the maximum of the GMM posterior probability for a given data point. To preserve the topological structure of the point sets, the GMM centroids are forced to move coherently as a group. The expectation maximization algorithm is used to optimize the cost function.^[3]

Let there be M points in ${\displaystyle \mathcal{M}}$ and N points in ${\displaystyle \mathcal{S}}$. The GMM probability density function for a point s is:

${\displaystyle p(s)=\sum _{i=1}^{M+1}P(i)p(s|i)}$

(cpd.1)

where, in D dimensions, ${\displaystyle p(s|i)}$ is the Gaussian distribution centered on point ${\displaystyle m_i\in \mathcal{M}}$.

$\text{Undefined control sequence lVert}$

The membership probabilities ${\displaystyle P(i)=\frac{1}{M}}$ is equal for all GMM components. The weight of the uniform distribution is denoted as ${\displaystyle w\in [0,1]}$. The mixture model is then:

${\displaystyle p(s)=w\frac{1}{N}+(1-w)\sum _{i=1}^M\frac{1}{M}p(s|i)}$

(cpd.2)

The GMM centroids are re-parametrized by a set of parameters ${\displaystyle \theta }$ estimated by maximizing the likelihood. This is equivalent to minimizing the negative log-likelihood function:

${\displaystyle E(\theta ,{\sigma }^2)=-\sum _{j=1}^N\log \sum _{i=1}^{M+1}P(i)p(s|i)}$

(cpd.3)

where it is assumed that the data is independent and identically distributed. The correspondence probability between two points ${\displaystyle m_i}$ and ${\displaystyle s_j}$ is defined as the posterior probability of the GMM centroid given the data point:

${\displaystyle P(i|s_j)=\frac{P(i)p(s_j|i)}{p(s_j)}}$

The expectation maximization (EM) algorithm is used to find ${\displaystyle \theta }$ and ${\displaystyle {\sigma }^2}$. The EM algorithm consists of two steps. First, in the E-step or estimation step, it guesses the values of parameters ("old" parameter values) and then uses Bayes' theorem to compute the posterior probability distributions ${\displaystyle P^{\text{old}}(i,s_j)}$ of mixture components. Second, in the M-step or maximization step, the "new" parameter values are then found by minimizing the expectation of the complete negative log-likelihood function, i.e. the cost function:

$\text{Undefined control sequence operatorname}$

(cpd.4)

Ignoring constants independent of ${\displaystyle \theta }$ and ${\displaystyle \sigma }$, Equation (cpd.4) can be expressed thus:

$\text{Undefined control sequence operatorname}$

(cpd.5)

where

${\displaystyle N_{\mathbf{P}}=\sum _{j=0}^N\sum _{i=0}^M{P}^{\text{old}}(i|s_j)\le N}$

with ${\displaystyle N=N_{\mathbf{P}}}$ only if ${\displaystyle w=0}$. The posterior probabilities of GMM components computed using previous parameter values ${\displaystyle P^{\text{old}}}$ is:

$\text{Undefined control sequence lVert}$

(cpd.6)

Minimizing the cost function in Equation (cpd.5) necessarily decreases the negative log-likelihood function E in Equation (cpd.3) unless it is already at a local minimum.^[3] Thus, the algorithm can be expressed using the following pseudocode, where the point sets ${\displaystyle \mathcal{M}}$ and ${\displaystyle \mathcal{S}}$ are represented as ${\displaystyle M\times D}$ and ${\displaystyle N\times D}$ matrices ${\displaystyle \mathbf{M}}$ and ${\displaystyle \mathbf{S}}$ respectively:^[3]

algorithm CPD[math]\displaystyle{ (\mathcal{M}, \mathcal{S}) }[/math] θ := θ0 initialize 0 ≤ w ≤ 1 [math]\displaystyle{ \sigma^2 := \frac{1}{DNM}\sum_{j=1}^N \sum_{i=1}^M \lVert s_j - m_i \rVert^2 }[/math] while not registered: // E-step, compute P for i ∊ [1, M] and j ∊ [1, N]: [math]\displaystyle{ p_{ij} := \frac {\exp \left( -\frac{1}{2\sigma^2} \lVert s_j - T(m_i, \theta)\rVert^2 \right)} {\sum_{k=1}^{M} \exp \left( -\frac{1}{2\sigma^2} \lVert s_j - T(m_k, \theta)\rVert^2 \right) + (2\pi \sigma^2)^\frac{D}{2} \frac{w}{1-w} \frac{M}{N}} }[/math] // M-step, solve for optimal transformation {θ, σ2} := solve(S, M, P) return θ 

where the vector ${\displaystyle \mathbf{1}}$ is a column vector of ones. The solve function differs by the type of registration performed. For example, in rigid registration, the output is a scale a, a rotation matrix ${\displaystyle \mathbf{R}}$, and a translation vector ${\displaystyle \mathbf{t}}$. The parameter ${\displaystyle \theta }$ can be written as a tuple of these:

${\displaystyle \theta =\{a,\mathbf{R},\mathbf{t}\}}$

which is initialized to one, the identity matrix, and a column vector of zeroes:

${\displaystyle {\theta }_0=\{1,\mathbf{I},\mathbf{0}\}}$

The aligned point set is:

${\displaystyle T(\mathbf{M})=a\mathbf{M}{\mathbf{R}}^T+\mathbf{1}{\mathbf{t}}^T}$

The solve_rigid function for rigid registration can then be written as follows, with derivation of the algebra explained in Myronenko's 2010 paper.^[3]

solve_rigid(S, M, P) NP := 1TP1 [math]\displaystyle{ \mu_s:=\frac{1}{N_\mathbf{P}}\mathbf{S}^T\mathbf{P}^T\mathbf{1} }[/math] [math]\displaystyle{ \mu_m:=\frac{1}{N_\mathbf{P}}\mathbf{M}^T\mathbf{P}\mathbf{1} }[/math] [math]\displaystyle{ \hat{\mathbf{S}}:=\mathbf{S} - \mathbf{1}\mu_s^T }[/math] [math]\displaystyle{ \hat{\mathbf{M}}:=\mathbf{M} - \mathbf{1}\mu_m^T }[/math] [math]\displaystyle{ \mathbf{A}:=\hat{\mathbf{S}^T}\mathbf{P}^T\hat{\mathbf{M}} }[/math] U, V := svd(A) // the singular value decomposition of A = UΣVT C := diag(1, …, 1, det(UVT)) // diag(ξ)is the diagonal matrix formed from vector ξ R := UCVT [math]\displaystyle{ a := \frac{\operatorname{tr}(\mathbf{A}^T\mathbf{R})}{\operatorname{tr}(\mathbf{\hat{\mathbf{M}}^T \operatorname{diag}(\mathbf{P}\mathbf{1})\hat{\mathbf{M}}})} }[/math] // tr is the trace of a matrix t := μs − aRμm [math]\displaystyle{ \sigma^2:=\frac{1}{N_\mathbf{P} D}(\operatorname{tr}(\mathbf{\hat{\mathbf{S}}^T \operatorname{diag}(\mathbf{P}^T\mathbf{1})\hat{\mathbf{S}}})-a\operatorname{tr}(\mathbf{A}^T\mathbf{R})) }[/math] return {a, R, t}, σ2 

For affine registration, where the goal is to find an affine transformation instead of a rigid one, the output is an affine transformation matrix ${\displaystyle \mathbf{B}}$ and a translation ${\displaystyle \mathbf{t}}$ such that the aligned point set is:

${\displaystyle T(\mathbf{M})=\mathbf{M}{\mathbf{B}}^T+\mathbf{1}{\mathbf{t}}^T}$

The solve_affine function for rigid registration can then be written as follows, with derivation of the algebra explained in Myronenko's 2010 paper.^[3]

solve_affine(S, M, P) NP := 1TP1 [math]\displaystyle{ \mu_s := \frac{1}{N_\mathbf{P}}\mathbf{S}^T\mathbf{P}^T\mathbf{1} }[/math] [math]\displaystyle{ \mu_m := \frac{1}{N_\mathbf{P}}\mathbf{M}^T\mathbf{P}\mathbf{1} }[/math] [math]\displaystyle{ \hat{\mathbf{S}} := \mathbf{S} - \mathbf{1}\mu_s^T }[/math] [math]\displaystyle{ \hat{\mathbf{M}} := \mathbf{M} - \mathbf{1}\mu_s^T }[/math] [math]\displaystyle{ \mathbf{B} := (\hat{\mathbf{S} }^T\mathbf{P}^T\hat{\mathbf{M} })(\hat{\mathbf{M} }^T\operatorname{diag}(\mathbf{P}\mathbf{1})\hat{\mathbf{M} })^{-1} }[/math] t := μs − Bμm [math]\displaystyle{ \sigma^2 := \frac{1}{N_\mathbf{P} D}(\operatorname{tr}(\hat{\mathbf{S} }^T \operatorname{diag}(\mathbf{P}^T\mathbf{1})\hat{\mathbf{S} })-\operatorname{tr}(\hat{\mathbf{S} }^T\mathbf{P}^T\hat{\mathbf{M} }\mathbf{B}^T)) }[/math] return {B, t}, σ2 

It is also possible to use CPD with non-rigid registration using a parametrization derived using calculus of variations.^[3]

Sums of Gaussian distributions can be computed in linear time using the fast Gauss transform (FGT).^[3] Consequently, the time complexity of CPD is ${\displaystyle O(M+N)}$, which is asymptotically much faster than ${\displaystyle O(MN)}$ methods.^[3]

Bayesian coherent point drift (BCPD)

A variant of coherent point drift, called Bayesian coherent point drift (BCPD), was derived through a Bayesian formulation of point set registration. ^[34] BCPD has several advantages over CPD, e.g., (1) nonrigid and rigid registrations can be performed in a single algorithm, (2) the algorithm can be accelerated regardless of the Gaussianity of a Gram matrix to define motion coherence, (3) the algorithm is more robust against outliers because of a more reasonable definition of an outlier distribution. Additionally, in the Bayesian formulation, motion coherence was introduced through a prior distribution of displacement vectors, providing a clear difference between tuning parameters that control motion coherence.

4.5. Sorting the Correspondence Space (SCS)

This algorithm was introduced in 2013 by H. Assalih to accommodate sonar image registration.^[35] These types of images tend to have high amounts of noise, so it is expected to have many outliers in the point sets to match. SCS delivers high robustness against outliers and can surpass ICP and CPD performance in the presence of outliers. SCS doesn't use iterative optimization in high dimensional space and is neither probabilistic nor spectral. SCS can match rigid and non-rigid transformations, and performs best when the target transformation is between three and six degrees of freedom.