1. Lewis Structure and Valence Bond Theory

The Lewis structure of H₂O describes the bonds as two sigma bonds between the central oxygen atom and the two peripheral hydrogen atoms with oxygen having two lone pairs of electrons. Valence bond theory suggests that H₂O is sp3 hybridized in which the 2s atomic orbital and the three 2p orbitals of oxygen are hybridized to form four new hybridized orbitals which then participate in bonding by overlapping with the hydrogen 1s orbitals. As such, the predicted shape and bond angle of sp3 hybridization is tetrahedral and 109.5°. This is in open agreement with the true bond angle of 104.45°. The difference between the predicted bond angle and the measured bond angle is traditionally explained by the electron repulsion of the two lone pairs occupying two sp3 hybridized orbitals. While valence bond theory is suitable for predicting the geometry and bond angle of H₂O, its prediction of electronic states does not agree with the experimentally measured reality. In the valence bond model, the two sigma bonds are of identical energy and so are the two lone pairs since they both resides in the same bonding and nonbonding orbitals, thus corresponding to two energy levels in the photoelectronic spectrum. In other words, if water was formed from two identical O-H bonds and two identical sp3 lone pairs on the oxygen atom as predicted by valence bond theory, then its photoelectron spectrum (PES) would have two (degenerate) peaks and energy, one for the two O-H bonds and the other for the two sp³ lone pairs. However, the photoelectronic spectrum of H₂O reveals four different energy levels that correspond to the ionization energies of the two bonding and two nonbonding pairs of elections at 12.6eV, 14.7eV, 18.5eV, and 32.2eV.^[1] This suggest that neither the two O-H bonds nor the two sp3 lone pairs are degenerate in energy.

2. Molecular Orbital Treatment of H₂O

Simple Molecular Orbital (MO) diagram of H₂O

Simple MO of H₂O

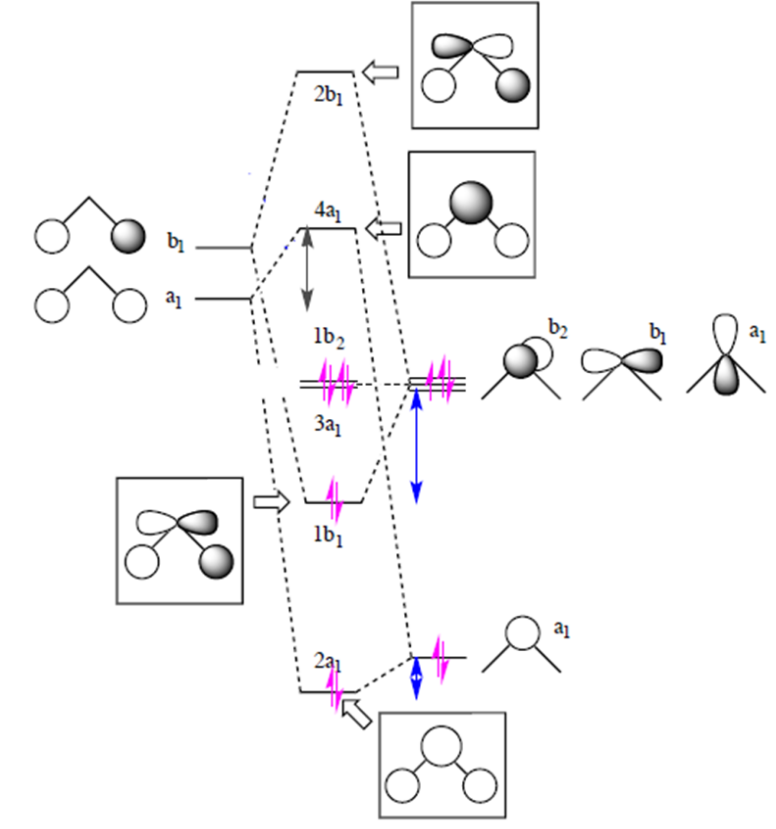
In contrast to localizing electrons within their atomic orbitals in valence bond theory, the molecular orbital approach considers electrons to be delocalized across the entire molecule. The simple MO diagram of H₂O is shown on the right.^[2][3] Following simple symmetry treatments, the 1s orbitals of hydrogen atom are premixed as a1 and b1. Orbitals of same symmetry and similar energy levels can then be mixed to form a new set of molecular orbitals with bonding, nonbonding, and antibonding characteristics. In the simple MO diagram of H₂O, the 2s orbital of oxygen is mixed with the premixed hydrogen orbitals, forming a new bonding (2a1) and antibonding orbital (4a1). Similarly, the 2p orbital (b1) and the other premixed hydrogen 1s orbitals (b1) are mixed to make bonding orbital 1b1 and antibonding orbital 2b1. The two remaining 2p orbitals are unmixed. While this simple MO diagram does not provide four different energy levels as experimentally determined from PES, the two bonding orbitals are nonetheless distinctly different thus providing differentiation on the bonding electron energy levels.  

Hybridized Molecular Orbital (MO) diagram of H₂O

To further distinguish the electron energy differences between the two non-bonding orbitals, orbital mixing can be further performed between the 2p (3a₁) orbital on oxygen and the antibonding 4a₁ orbital since they are of the same symmetry and close in energy level. Mixing these two orbitals affords two new sets of orbitals as shown in the right boxed in red. Significant mixing of these two orbitals results in both energy changes and changes in the shape of the molecular orbital.^[4] There's now significant sp hybridization characterization that is previously not present in the simple MO diagram. Consequently, the two nonbonding orbitals are now at different energies,^[5] providing the four distinct energy levels consistent with the PES. Alternatively, instead of mixing the 3a₁ nonbonding orbital with the 4a₁ antibonding orbital, one can also mix the 3a₁ nonbinding orbital with the 2a₁ bonding orbital to produce a similar MO diagram of H₂O. This alternative H₂O MO diagram can also be derived by performing the Walsh diagram treatment via adjusting bonding geometry from linear to bent shape. In addition, these MO diagrams can be generated from bottom up by first hybridizing the oxygen 2s and 2p orbitals (assume sp² hybridization) and then mixing orbitals of same symmetry. For simple molecules, pictorially generating their MO diagram can be achieved without extensive knowledge of point group theory and using reducible and irreducible representations.

Hybridized MO of H₂O

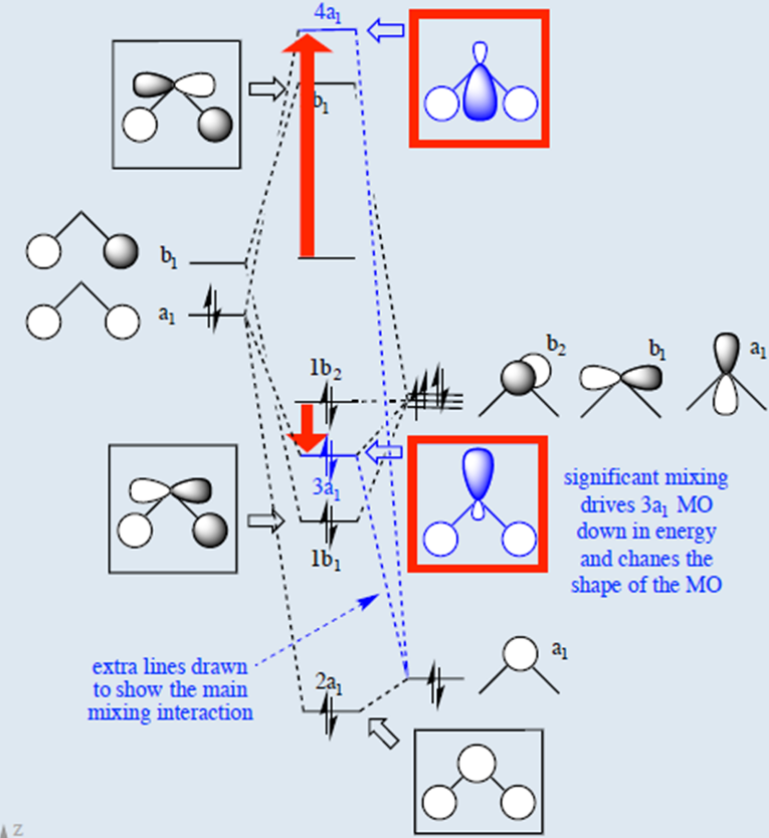
Note that the size of the atomic orbitals in the final molecular orbital are different from the size of the original atomic orbitals, this is due to different mixing proportions between the oxygen and hydrogen orbitals since their initial atomic orbital energies are different. In other words, when two orbitals mix, the amount the orbitals mix is inversely proportional to the initial difference in energy of the orbitals. Therefore, orbitals which are initially close in energy mix (i.e. interact) more than orbitals which are initially far apart in energy. When two orbitals of different energy mix (i.e. interact), the low energy combination resembles more the initial low energy orbital; the higher energy combination resembles more the initial high energy orbital. When two orbitals can interact and they are of the same initial energy, then the two resultant combination orbitals are derived equally from the two initial orbitals. (Second order perturbation theory).^[6] In addition, while the valence bond theory predicts H₂O is sp³ hybridized, the prediction from MO theory is more complex. Since the 2p_z orbital is not involved at all in interactions with the hydrogen atoms and becomes an unhydridized lone pair (n_O^(π)), one would argue H₂O is sp² hybridized. This would be true under the idealized assumption that s and p character are evenly distributed between the two O-H bonds and O lone pair (n_O^(σ)). However, this prediction (120° bond angles) is inconsistent with the bond angle of H₂O being 104.5°. The actual hybridization of H₂O can be explained via the concept of isovalent hybridization or Bent's rule. In short, s character is accumulated in lone pair orbitals because s character is energy lowering relative to p character, and lone pair electrons are closely held with unshared electron density. In contrast, bonding pairs are localized further away and electron density is shared with another atom, so additional s character does not lower energy quite as effectively.  Hence, comparatively more p character is distributed into the bonding orbitals.

Walsh Diagram treatment of H₂O

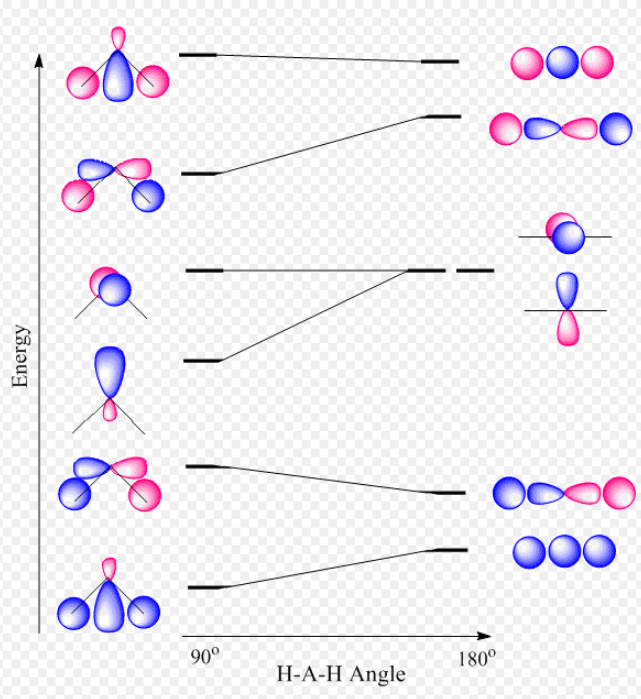
3. Isovalent Hybridization and Bent's Rule

Isovalent hybridization refers to advanced or second order atomic orbital mixing that does not produce simple sp, sp2, and sp3 hybridization schemes. For molecules with lone pairs, the bonding orbitals are isovalent hybrids since different fractions of s and p orbitals are mixed to achieve optimal bonding. Isovalent hybridization is used to explain bond angles of those molecules that is inconsistent with the generalized simple sp, sp2 and sp3 hybridization. For molecules containing lone pairs, the true hybridization of these molecules depends on the amount of s and p characters of the central atom which is related to its electronegativity. "According to Bent's rule, as the substituent electronegativies increase, orbitals of greater p character will be directed towards those groups. By the above discussion, this will decrease the bond angle. In predicting the bond angle of water, Bent’s rule suggests that hybrid orbitals with more s character should be directed towards the very electropositive lone pairs, while that leaves orbitals with more p character directed towards the hydrogens. This increased p character in those orbitals decreases the bond angle between them to less than the tetrahedral 109.5°."

4. Molecular Orbital Theory Versus Valence Bond Theory

Molecular Orbital Theory vs. Valence Bond Theory has been a topic of debate since the early to mid 1900's. Despite continued heated debate on which model more accurately depict the true bonding scheme of molecules, scientists now view MO and VB theories as complementary and teammates. With the development of modern high speed computers and advanced molecular modeling programs, both MO and VB theories are used widely today, though for generally different purposes. In general, MO theory can accurately predict the ground state energy of the system, the different electronic states energies of bonding and nonbonding orbitals, and magnetic and ionization properties in a straight forward manner. On the other hand, VB theory is traditionally useful for predicting bond angle and mechanism drawing. Modern valence bond theory can provide the same electronic information obtained by MO theory, though the process is more complicated. In addition, modern VB theory can also predict excited states energies in which MO theory cannot easily achieve. The truth is, both theories are equally important in understanding chemical bonding that while neither theory is completely comprehensive, the two together nonetheless provides a in-depth model for chemical bonds. In the words of Roald Hoffmann:^[7] "Taken together, MO and VB theories constitute not an arsenal, but a tool kit... Insistence on a journey... equipped with one set of tools and not the other puts one at a disadvantage. Discarding any one of the two theories undermines the intellectual heritage of chemistry."^[8][9]

In short, valence bond theory and MO theory are at core, a manifestation of the Heisenberg Uncertainty Principle. When treating electrons in localized orbitals (VB theory), one can fairly accurately predict and measure its shape, geometry and position, but cannot accurately predict its energy and momentum. When treating electrons in delocalized orbitals (MO theory), one gains more measurements on its energy and momentum, but loses accuracy on its position. In other words, MO and VB theory should be used appropriately depending on what one wishes to measure.