Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
David Rhoades
 -- 3052 2022-10-18 02:50:47 |
2 format
Jason Zhu
 + 1 word(s) 3053 2022-10-18 03:25:56 | |
3 format
Jason Zhu
 Meta information modification 3053 2022-10-21 04:10:20 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Rhoades, D.A.;  Rastin, S.J.;  Christophersen, A. “Every Earthquake a Precursor According to Scale” Model. Encyclopedia. Available online: https://encyclopedia.pub/entry/29730 (accessed on 05 May 2024).
Rhoades DA,  Rastin SJ,  Christophersen A. “Every Earthquake a Precursor According to Scale” Model. Encyclopedia. Available at: https://encyclopedia.pub/entry/29730. Accessed May 05, 2024.
Rhoades, David A., Sepideh J. Rastin, Annemarie Christophersen. "“Every Earthquake a Precursor According to Scale” Model" Encyclopedia, https://encyclopedia.pub/entry/29730 (accessed May 05, 2024).
Rhoades, D.A.,  Rastin, S.J., & Christophersen, A. (2022, October 18). “Every Earthquake a Precursor According to Scale” Model. In Encyclopedia. https://encyclopedia.pub/entry/29730
Rhoades, David A., et al. "“Every Earthquake a Precursor According to Scale” Model." Encyclopedia. Web. 18 October, 2022.
“Every Earthquake a Precursor According to Scale” Model
Edit
This entry is adapted from the peer-reviewed paper 10.3390/geosciences12090349

The observation that major earthquakes are generally preceded by an increase in the seismicity rate on a timescale from months to decades was embedded in the “Every Earthquake a Precursor According to Scale” (EEPAS) model. EEPAS has since been successfully applied to regional real-world and synthetic earthquake catalogues to forecast future earthquake occurrence rates with time horizons up to a few decades. When combined with aftershock models, its forecasting performance is improved for short time horizons. As a result, EEPAS has been included as the medium-term component in public earthquake forecasts in New Zealand. EEPAS has been modified to advance its forecasting performance despite data limitations. One modification is to compensate for missing precursory earthquakes. Precursory earthquakes can be missing because of the time-lag between the end of a catalogue and the time at which a forecast applies or the limited lead time from the start of the catalogue to a target earthquake. An observed space-time trade-off in precursory seismicity, which affects the EEPAS scaling parameters for area and time, also can be used to improve forecasting performance. Systematic analysis of EEPAS performance on synthetic catalogues suggests that regional variations in EEPAS parameters can be explained by regional variations in the long-term earthquake rate.

statistical seismology earthquake precursors precursory seismicity

1. Introduction

Understanding the earthquake generation process and development of earthquake forecasting models are among the main goals of statistical seismology [1][2]. Achieving these goals requires contributions from both physical and statistical modelling. In statistical seismology major laws, including the Omori-Utsu law for aftershock rate decay [3][4] and the Gutenberg-Richter magnitude frequency law [5], were originally derived empirically as statistical relations. However, it took a long time for them to be interpreted in terms of the physics of the earthquake generation process [6][7][8][9][10][11][12]. The “Every Earthquake a Precursor According to Scale” (EEPAS) model is also based on empirical statistical relations. While researchers have learned a lot about these relations, researchers still have much to learn about their physical origin. The same holds for other attempts at predicting earthquakes like that of natural time analysis of seismicity [13].
EEPAS is a space-time point process model based on an increase of minor earthquake occurrences preceding major earthquakes, the so-called “precursory scale increase” (Ψ-) phenomenon. It employs associated predictive scaling relations of the Ψ-phenomenon to forecast future earthquake rates [14][15]. Since its introduction in 2004, EEPAS has been fitted and tested on the earthquake catalogues of New Zealand, California, Japan, and Greece [16][17][18][19][20][21][22]. It was also tested by the Collaboratory for the Study of Earthquake Predictability (CSEP), an international collaboration to test earthquake forecasting models prospectively and transparently [23]. A CSEP-compatible version of EEPAS, with three-month updating, was submitted to several regional CSEP testing centres [20][21][24][25][26]. The EEPAS model generally performs better than time-invariant models of seismicity [25][26]. It is designed to forecast the largest earthquakes in a region in the medium term—a period ranging from months to decades, depending on magnitude. EEPAS is not a complete model of seismicity, because it does not consider short-term clustering. However, when combined with short-term and time-invariant forecasting models, it has proven to provide a practical method for forecasting earthquakes over a wide range of timescales [27][28][29].
EEPAS has progressively evolved both to compensate for data limitations and enhance earthquake forecasting in combination with other models. The main motivation behind all types of EEPAS revisions is to enhance the forecasting performance, i.e., the information gain. Furthermore, in recent years the understanding about additional factors affecting the information gain, other than data limitations, has developed. Consequently, researchers have incorporated these aspects into the EEPAS model.

2. Empirical Foundations—The Ψ-Phenomenon

The Ψ-phenomenon is an increase in the rate and magnitude of minor earthquakes observed to occur before most major earthquakes in well-catalogued regions [14][15]. The precursor time—the time interval between the onset of the increase and major earthquake—can range from months to decades, depending on the magnitude of the major earthquake. In [15], the Ψ-phenomenon was identified for 47 major earthquakes in California and northern Mexico, Japan, Greece and northwest Turkey, and New Zealand. The onset of precursory seismicity was identified by a minimum of a cumulative magnitude anomaly (cumag) plot, in which all earthquakes in a region surrounding the major earthquake and its aftershocks over an extended time period preceding the occurrence of the major earthquake were analysed.
In [15], predictive scaling relations were identified from the 47 examples of Ψ. These are of the form:
The first two of these relations had been known since 1977 for the precursory swarm phenomenon [30][31][32][33][34], the forerunner and a special case of the Ψ-phenomenon. Precursory swarms are an example of “precursors of the second kind”, as designated by Rikitake [35][36][37]. It shared this classification with numerous geophysical precursors for which the logarithm of precursor time was linearly related to the mainshock magnitude. The Rikitake relation was not predictive, since neither the precursor time nor the mainshock magnitude were known before the mainshock occurred. A useful feature of precursory swarms was that each swarm had an associated MP from which Mm and TP of a future earthquake, or earthquakes, could be predicted (Equation (1)). It was through the learnings from extensive testing of the precursory swarm hypothesis in forecasting specific major earthquakes [38][39][40][41][42][43][44][45][46] that the more general Ψ-phenomenon was eventually recognized. The Ψ-phenomenon, unlike the precursory swarm, could not be readily identified before the occurrence of a major earthquake. Consequently, the EEPAS model was created to produce non-specific earthquake forecasts using the Ψ predictive scaling relations. EEPAS provides a generic statistical framework that regards every earthquake as a precursor of subsequent larger earthquakes. The result is a non-stationary model, which bears some similarities to the Epidemic-type-Aftershock (ETAS) model [47][48]. However, unlike ETAS, there is no suggestion that one earthquake triggers another. Instead, the magnitude of each earthquake is considered as a value of MP, i.e., a seismogenic process is assumed to be taking place on the associated scales of time, magnitude, and location indicated by equation.

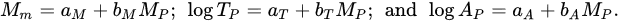
3. Combinations and Extensions to Accommodate Aftershocks

3.1. STEP-EEPAS Mixture

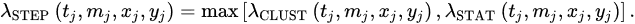
The Short-Term Earthquake Probabilities (STEP) [49] model is an aftershock model based on the Omori–Utsu aftershock-decay relation [4]. The STEP model has a background component, λSTAT, and a time-dependent clustering component, λCLUST. The expected number of earthquakes in the jth time, magnitude, location bin (tj,mj, xj,yj) is given by 

STEP and EEPAS were linearly combined to enhance short-term earthquake forecasting in California [50]. Using the Advanced National Seismic System (ANSS) catalogue of California over the period 1984–2004, the optimal mixture model for forecasting earthquakes with M ≥5:0 was found to be a convex linear combination consisting of 0.42 of EEPAS and 0.58 of STEP. This mixture gave an average probability gain of more than 2 (i.e., information gain per earthquake, ln(probability gain), of more than 0.7) compared to each of the individual models when forecasting ahead for the next 24 h time period. The contribution from EEPAS can be weighted depending on magnitude to enhance the performance at high target magnitudes. The STEP-EEPAS mixture improves short-term forecasting by allowing for the aftershocks of earthquakes that have already occurred.

3.2. EEPAS with Aftershocks Model

The EEPAS with aftershocks model (EAS) [51] has a different purpose than the STEP-EEPAS mixture. It allows for aftershocks of earthquakes expected to occur under the EEPAS model, but not for aftershocks of earthquakes that have already occurred. It is aimed at improving medium-term forecasts by including the associated aftershocks of expected mainshocks in the forecast. The model assumes that the number of expected aftershocks depends on the mainshock magnitude, that their magnitude distribution follows the Gutenberg-Richter relation [52], and their spatial distribution is consistent with Utsu’s areal relation [53]. This involves a modification of the EEPAS model to include several additional parameters: the Gutenberg-Richter b-value for aftershocks, an aftershock productivity parameter θ, the minimum magnitude difference γ by which a mainshock exceeds its largest aftershock, and the proportion pM of earthquakes in the target magnitude range that are mainshocks. The effect is to change the magnitude and spatial distributions of the transient contributions of precursors to the rate density. Versions of the EEPAS and EAS model with equal weights and aftershocks down-weighted were fitted to a 10-year period and independently tested on a later 10-year period of the catalogues of California and the Kanto region of central Japan [51]. For the testing period, the information gain of the EAS models over their EEPAS counterparts was about 0.1 on average. This confirmed the efficacy of the modifications. However, the expected number of aftershocks was found to strongly depend on the assumed maximum magnitude. This creates a difficulty in the practical application of the EAS model.

3.3. Janus Model: EEPAS-ETAS Mixture

The Janus model is an additive mixture of the EEPAS model and an Epidemic-type aftershock (ETAS) model. From each contributing earthquake, it looks both to the larger earthquakes expected to follow it in the medium term and mostly smaller earthquakes expected to follow it in the short term. In [54], the Janus model was optimized for time horizons ranging from 0–3000 days (i.e., up to more than 8 years) on the New Zealand and California earthquake catalogues. For each time horizon of interest, EEPAS parameters were refitted with the delay set equal to the time horizon. It was found that the ETAS model is much more informative than EEPAS for forecasting with short-time horizons of a few days, but even with a zero-time horizon, the Janus model outperforms it with an information gain per earthquake (IGPE) of about 0.1. For time horizons of 10–3000 days, the Janus model outperforms both ETAS and EEPAS with IGPEs ranging from 0.2 to 0.5. As the time horizon lengthens beyond six months in New Zealand and two years in California, the EEPAS model becomes more informative than ETAS and the major component of the optimal mixture. In [54], it was concluded that both cascades of triggering and the precursory scale increase phenomenon contribute to earthquake predictability and that these contributions are largely independent.

3.4. Hybrid Forecasting in New Zealand

EEPAS is now used for public earthquake forecasting in New Zealand, as one of the core elements of a hybrid forecasting tool. Public forecasting was initiated in New Zealand as a response to the devastating Canterbury earthquake sequence. This sequence began with the September 2010 M7.1 Darfield earthquake [55] and continued with the 22 February 2011 M6.3 Christchurch earthquake [56]. The Christchurch earthquake and subsequent earthquakes of about M6 in the vicinity of Christchurch resulted in the death of 185 people, and over NZ40 billion dollars of damage to buildings and infrastructure [57]. The faults that ruptured during this sequence were unknown prior to the sequence and hazard was considered to be low in Christchurch [58]. As a result of this sequence, attention was drawn to statistical forecasting models. A model with time-varying and long-term components was developed to forecast the following 50 years of expected earthquakes and resulting hazard in Canterbury. This was used to inform decisions for the rebuilding of Christchurch [28]. The time-varying component was provided by a mixture of EEPAS and aftershock models and time-invariant component by a mixture of different smoothed seismicity models [29][59]. Such statistical modelling can serve as a supplement to standard probabilistic seismic hazard analysis (PSHA) (e.g., [58][60]).
Following the November 2016 M7.8 Kaikoura earthquake [61], a modified hybrid model with three components—short-term, medium-term and long-term—was developed [27] to forecast the expected earthquakes and resulting hazard over the following 100 years. This model was used to inform decision-makers involved in the reinstatement of road and rail networks in the northern South Island. It is a gridded model, in which EEPAS provides the medium-term component. 

4. Challenges in EEPAS Forecasting

Since its introduction in 2004, EEPAS has been a successful forecasting model for well-catalogued regions including New Zealand [16][24][26][27][54][62][63], California [16][20][25][54][64], Japan [17][18][21][22][65], and Greece [19]. To address the limitations imposed by the input earthquake catalogues, EEPAS has undergone many revisions. As mentioned earlier, one milestone in the EEPAS improvement was compensation of the forecasts for missing precursory earthquakes in the time-lag between the end of the catalogue and the forecasting time-horizon. researchers have also learned how to compensate EEPAS forecasts for the limited record of precursory information before any target earthquake. Overall, the current version of the EEPAS is much better adapted to deal with the limitations of any earthquake catalogue than previously. However, there are still significant challenges and unknowns as outlined here.

4.1. Understanding the Physics behind the Ψ-Phenomenon

The Ψ-phenomenon and EEPAS model are empirically based. However, the Ψ-phenomenon can be identified as easily in synthetic catalogues as in real earthquake catalogues and the EEPAS model also works well in synthetic catalogues [66][67]. Synthetic catalogues are based on physical components such as fault networks, slip rates on faults, friction laws, and Coulomb stress calculations [68][69]. The earthquake generation process of each synthetic earthquake is in principle traced through the stress transfer between neighbouring faults. This leads to an eventual failure of the fault that produces the earthquake. Ideally, the origin of the Ψ-phenomenon should be explained by a similar physics-based concept. Such an understanding is likely to be helpful in guiding future refinements of the EEPAS model.

4.2. Incorporating Dependence on the Long-Term Earthquake Rate

researchers have learned from analysis of synthetic catalogues that the scale of the EEPAS time distribution is inversely proportional to the slip rate on faults. Slip rates are related to the long-term rate of the earthquakes that they generate [70]. Therefore, researchers should expect the scale of the EEPAS time distribution to be inversely related to the long-term earthquake rate.
If the spatial variability of the long-term earthquake rate is known, it can be incorporated into the EEPAS model using Equation (19). This is straight-forward and does not add to the number of fitted parameters in the model. The challenge is how to best estimate it from existing data sources [71]. The long-term earthquake rates can be estimated from smoothed seismicity, strain rates, faults and their slip rates, the location of plate boundaries, or some combinations of these. The main limitation is the restricted length of the available catalogue against which to test them.

4.3. A Three-Dimensional Version of EEPAS?

The EEPAS model at present only makes use of two spatial dimensions—latitude and longitude. All earthquakes within a chosen depth range are treated the same, regardless of their estimated hypocentral depths. The reason for this is primarily that depth determinations are often poorly constrained. In the New Zealand catalogue, many depths are fixed by analysts, rather than directly estimated, because of the difficulty of estimating depths using a 2D velocity model and the available seismograph network. researchers expect that the seismograph network will become denser over time and a comprehensive 3D velocity model [72] will be incorporated in the GeoNet earthquake locator. As a result, the precision of depth determinations will improve. Then, it will make sense to shift to three-dimensional distance determinations in the EEPAS model.

4.4. Target-Earthquake Oriented Compensation for Missing Precursors

Researchers have shown how to compensate EEPAS for missing earthquakes with a fixed lead time. However, applying a fixed lead time is potentially wasteful of precious earthquake catalogue data. Ignoring the early earthquakes in a catalogue can adversely affect the forecasting of large earthquakes, which have very long precursor times. It is the largest earthquakes that researchers are ultimately most interested in forecasting, even though conformity to the Gutenberg-Richter law limits their contribution to the information gain.
The challenge is then to use as much of the past catalogue as possible and compensate the forecast of each target earthquake for the incompleteness of precursory contributions at each point in time, location, and magnitude. This is what researchers call “target-oriented” compensation. Shifting from a fixed lead time to target-oriented compensation would involve modifying Equations.
The incompleteness of precursory contributions for each target earthquake depends on the completeness of the catalogue in its vicinity in the period prior to its occurrence.

4.5. Accommodating Variable Incompleteness of the Earthquake Catalogue

Completeness of an earthquake catalogue varies with time, magnitude, and location depending on the network configuration and instrumentations [73]. Treatments of catalogue completeness can range from simple to elaborate. In the simplest approach, one might choose a starting time t0 after which the input catalogue is approximately complete for all magnitudes above a minimum threshold m0. Target-oriented compensation could then be applied based on the lead time between t0 and the time of each target earthquake. A more elaborate approach would be to estimate a magnitude-dependent starting time t0(m) at which the catalogue becomes complete for magnitude m>m0. The lead time L(m) for a given target earthquake then varies with the input magnitude. Furthermore, one can also take into account the effect of spatial variations on the catalogue completeness, due to time-varying coverage of the region of interest by the seismic network. at which the catalogue is complete for input magnitudes m>m0 and the resulting variable lead times L(m) at the time when a target earthquake occurs.

4.6. Optimal Use of the Space-Time Trade-Off

The space-time trade-off of precursory seismicity presents opportunities to improve EEPAS forecasts by mixing models from points on the line of even trade-off, as previously demonstrated [64]. However, optimally incorporating the trade-off into the EEPAS model remains a challenge. The space-time trade-off imposes a relation between the fitted values aT and σA. However, it may also affect other parameters, such as σT.
It is undesirable to incorporate the trade-off subjectively. Ideally, a revised fitting process would automatically integrate contributions to the forecast from points along the line. This would require some reformulation of the model.

4.7. Development of a Global Forecasting Model

An important goal for the future is the development of a global EEPAS model. The aim is to forecast the largest earthquakes, e.g., M≥7, expected to occur anywhere in the world, with time horizons extending out to several decades, using a global catalogue. All factors now known to affect the EEPAS parameters—incompleteness of precursory earthquakes, the space-time trade-off, and dependence on long-term earthquake rates—need to be simultaneously addressed in a coherent way to develop such a global model.
The model would be regionally adjustable to accommodate variation in the earthquake rate and the space-time trade-off of precursory seismicity. It would also include compensation for incompleteness of precursory contributions. The earthquake occurrence rates vary by several orders of magnitude between plate-boundary regions and continental regions. The time distribution in the EEPAS model would therefore vary over a similarly wide range. This induces far more variability in completeness of precursory contributions than in regional catalogues that adds to the challenge. These complexities imply there is still some way to go to develop a global EEPAS model.

References

  1. Vere-Jones, D.; Ben-Zion, Y.; Zúñiga, R. Statistical Seismology. Pure Appl. Geophys. 2005, 162, 1023–1026.
  2. Vere-Jones, D. Foundations of Statistical Seismology. Pure Appl. Geophys. 2010, 167, 645–653.
  3. Omori, F. On the aftershocks of earthquakes. J. Coll. Sci. Imp. Univ. Tokyo 1885, 7, 111–200.
  4. Utsu, T.; Ogata, Y. The centenary of the Omori formula for a decay law of aftershock activity. J. Phys. Earth 1995, 43, 1–33.
  5. Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188.
  6. Lindman, M.; Lund, B.; Roberts, R.; Jonsdottir, K. Physics of the Omori law: Inferences from interevent time distributions and pore pressure diffusion modeling. Tectonophysics 2006, 424, 209–222.
  7. Hainzl, S.; Marsan, D. Dependence of the Omori-Utsu law parameters on main shock magnitude: Observations and modeling. J. Geophys. Res. Solid Earth 2008, 113, B10309.
  8. Guglielmi, A.V. Interpretation of the Omori law. Izv. Phys. Solid Earth 2016, 52, 785–786.
  9. Faraoni, V. Lagrangian formulation of Omori’s law and analogy with the cosmic Big Rip. Eur. Phys. J. C 2020, 80, 445.
  10. Mogi, K. Magnitude-Frequency Relation for Elastic Shocks Accompanying Fractures of Various Materials and Some Related problems in Earthquakes (2nd Paper). Bull. Earthq. Res. Inst. Univ. Tokyo 1963, 40, 831–853.
  11. Schorlemmer, D.; Wiemer, S.; Wyss, M. Variations in earthquake-size distribution across different stress regimes. Nature 2005, 437, 539–542.
  12. Amitrano, D. Variability in the power-law distributions of rupture events. Eur. Phys. J. Spec. Top. 2012, 205, 199–215.
  13. Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Christopoulos, S.-R.G.; Lazaridou-Varotsos, M.S. Identifying the occurrence time of an impending mainshock: A very recent case. Earthq. Sci. 2015, 28, 215–222.
  14. Evison, F.; Rhoades, D. Precursory scale increase and long-term seismogenesis in California and Northern Mexico. Ann. Geophys. 2002, 45, 479–495.
  15. Evison, F.F.; Rhoades, D.A. Demarcation and Scaling of Long-term Seismogenesis. Pure Appl. Geophys. 2004, 161, 21–45.
  16. Rhoades, D.A.; Evison, F.F. Long-range earthquake forecasting with every earthquake a precursor according to scale. Pure Appl. Geophys. 2004, 161, 47–72.
  17. Rhoades, D.A.; Evison, F.F. Test of the EEPAS Forecasting Model on the Japan earthquake catalogue. Pure Appl. Geophys. 2005, 162, 1271–1290.
  18. Rhoades, D.A.; Evison, F.F. The EEPAS forecasting model and the probability of moderate-to-large earthquakes in central Japan. Tectonophysics 2006, 417, 119–130.
  19. Console, R.; Rhoades, D.A.; Murru, M.; Evison, F.F.; Papadimitriou, E.E.; Karakostas, V.G. Comparative performance of time-invariant, long-range and short-range forecasting models on the earthquake catalogue of Greece. J. Geophys. Res. Solid Earth 2006, 111, B09304.
  20. Rhoades, D.A. Application of the EEPAS model to forecasting earthquakes of moderate magnitude in southern California. Seismol. Res. Lett. 2007, 78, 110–115.
  21. Rhoades, D.A. Application of a long-range forecasting model to earthquakes in the Japan mainland testing region. Earth Planets Space 2011, 63, 197–206.
  22. Rhoades, D.A.; Somerville, P.G.; Somerville, F.; de Oliveira, D.; Thio, H.K. Effect of tectonic setting on the fit and performance of a long-range earthquake forecasting model. Res. Geophys. 2012, 2, 13–23.
  23. Zechar, J.D.; Schorlemmer, D.; Liukis, M.; Yu, J.; Euchner, F.; Maechling, P.J.; Jordan, T.H. The Collaboratory for the Study of Earthquake Predictability perspective on computational earthquake science. Concurr. Comput. Pract. Exp. 2010, 22, 1836–1847.
  24. Gerstenberger, M.C.; Rhoades, D.A. New Zealand earthquake forecast testing centre. In Seismogenesis and Earthquake Forecasting: The Frank Evison Volume II; Springer: Berlin/Heidelberg, Germany, 2010; pp. 23–38.
  25. Schneider, M.; Clements, R.; Rhoades, D.; Schorlemmer, D. Likelihood- and residual-based evaluation of medium-term earthquake forecast models for California. Geophys. J. Int. 2014, 198, 1307–1318.
  26. Rhoades, D.A.; Christophersen, A.; Gerstenberger, M.C.; Liukis, M.; Silva, F.; Marzocchi, W.; Werner, M.J.; Jordan, T.H. Highlights from the first ten years of the New Zealand Earthquake Forecast Testing Center. Seismol. Res. Lett. 2018, 89, 1229–1237.
  27. Gerstenberger, M.; Rhoades, D.; Litchfield, N.; Van Dissen, R.; Abbot, E.; Goded, T.; Christophersen, A.; Bannister, S.; Barrell, D.; Bruce, Z.; et al. The Kaikoura Seismic Hazard Model. N. Z. J. Geol. Geophys. 2022. in revision.
  28. Gerstenberger, M.; McVerry, G.; Rhoades, D.; Stirling, M. Seismic Hazard Modeling for the Recovery of Christchurch. Earthq. Spectra 2014, 30, 17–29.
  29. Rhoades, D.A.; Liukis, M.; Christophersen, A.; Gerstenberger, M.C. Retrospective tests of hybrid operational earthquake forecasting models for Canterbury. Geophys. J. Int. 2015, 204, 440–456.
  30. Evison, F.F. The precursory earthquake swarm. Phys. Earth Planet. Inter. 1977, 15, 19–23.
  31. Evison, F.F. Precursory seismic sequences in New Zealand. N. Z. J. Geol. Geophys. 1977, 20, 129–141.
  32. Evison, F.F. Fluctuations of seismicity before major earthquakes. Nature 1977, 266, 710–712.
  33. Evison, F. Multiple earthquake events at moderate-to-large magnitudes in Japan. J. Phys. Earth 1981, 29, 327–339.
  34. Evison, F. Generalised Precursory Swarm Hypothesis. J. Phys. Earth 1982, 30, 155–170.
  35. Rikitake, T. Earthquake precursors. Bull. Seismol. Soc. Am. 1975, 65, 1133–1162.
  36. Rikitake, T. Classification of earthquake precursors. Tectonophysics 1979, 54, 293–309.
  37. Rikitake, T. Earthquake Forecasting and Warning; Dordrecht Boston: D. Reidel; Hingham, Mass.: Sold and distributed in the U.S.A. and Canada by Kluwer Boston; Center for Academic Publications Japan: Tokyo, Japan, 1982.
  38. Rhoades, D.A.; Evison, F.F. Long-range earthquake forecasting based on a single predictor. Geophys. J. Int. 1979, 59, 43–56.
  39. Evison, F.F.; Rhoades, D.A. The precursory earthquake swarm in New Zealand: Hypothesis tests. N. Z. J. Geol. Geophys. 1993, 36, 51–60.
  40. Rhoades, D.A.; Evison, F.F. Long-range earthquake forecasting based on a single predictor with clustering. Geophys. J. Int. 1993, 113, 371–381.
  41. Evison, F.F.; Rhoades, D.A. The precursory earthquake swarm in New Zealand: Hypothesis tests. N. Z. J. Geol. Geophys. 1997, 40, 537–547.
  42. Evison, F.F.; Rhoades, D.A. Long-term seismogenic process for major earthquakes in subduction zones. Phys. Earth Planet. Inter. 1998, 108, 185–199.
  43. Evison, F.F.; Rhoades, D.A. The precursory earthquake swarm and the inferred precursory quarm. N. Z. J. Geol. Geophys. 1999, 42, 229–236.
  44. Evison, F.F.; Rhoades, D.A. The precursory earthquake swarm in Japan: Hypothesis test. Earth Planets Space 1999, 51, 1267–1277.
  45. Evison, F.; Rhoades, D. The precursory earthquake swarm in Greece. Ann. Geophys. 2000, 43, 991–1009.
  46. Evison, F.; Rhoades, D. Model of long-term seismogenesis. Ann. Geophys. 2001, 44, 81–93.
  47. Ogata, Y. Statistical model for standard seismicity and detection of anomalies by residual analysis. Tectonophysics 1989, 169, 159–174.
  48. Ogata, Y. Space-Time Point-Process Models for Earthquake Occurrences. Ann. Inst. Stat. Math. 1998, 50, 379–402.
  49. Gerstenberger, M.C.; Wiemer, S.; Jones, L.M.; Reasenberg, P.A. Real-time forecasts of tomorrow’s earthquakes in California. Nature 2005, 435, 328–331.
  50. Rhoades, D.A.; Gerstenberger, M.C. Mixture models for improved short-term earthquake forecasting. Bull. Seismol. Soc. Am. 2009, 99, 636–646.
  51. Rhoades, D.A. Long-range earthquake forecasting allowing for aftershocks. Geophys. J. Int. 2009, 178, 244–256.
  52. Gutenberg, B.; Richter, C.F. Seismicity of the Earth and Associated Phenomena; Princeton, N.J., Ed.; Princeton University Press: Princeton, NJ, USA, 1954.
  53. Utsu, T. A statistical study on the occurrence of aftershocks. Geophys. Mag. 1961, 30, 521–605.
  54. Rhoades, D.A. Mixture Models for Improved Earthquake Forecasting with Short-to-Medium Time Horizons. Bull. Seismol. Soc. Am. 2013, 103, 2203–2215.
  55. Gledhill, K.; Ristau, J.; Reyners, M.; Fry, B.; Holden, C. The Darfield (Canterbury) earthquake of September 2010: Preliminary seismological report. Bull. N. Z. Soc. Earthq. Eng. 2010, 43, 215–221.
  56. Kaiser, A.; Holden, C.; Beavan, J.; Beetham, D.; Benites, R.; Celentano, A.; Collett, D.; Cousins, J.; Cubrinovski, M.; Dellow, G.; et al. The Mw 6.2 Christchurch earthquake of February 2011: Preliminary report. N. Z. J. Geol. Geophys. 2012, 55, 67–90.
  57. Yan, W.; Galloway, W. Rethinking Resilience, Adaptation and Transformation in a Time of Change; Springer International Publishing: Berlin, Germany, 2017.
  58. Stirling, M.; McVerry, G.H.; Gerstenberger, M.C.; Litchfield, N.J.; Van Dissen, R.J.; Berryman, K.R.; Barnes, P.; Wallace, L.M.; Villamor, P.; Langridge, R.M.; et al. National Seismic Hazard Model for New Zealand: 2010 Update. Bull. Seismol. Soc. Am. 2012, 102, 1514–1542.
  59. Gerstenberger, M.C.; Rhoades, D.A.; McVerry, G.H. A hybrid time-dependent probabilistic seismic-hazard model for Canterbury, New Zealand. Seismol. Res. Lett. 2016, 87, 1311–1318.
  60. Meletti, C.; Galadini, F.; Valensise, G.; Stucchi, M.; Basili, R.; Barba, S.; Vannucci, G.; Boschi, E. A seismic source zone model for the seismic hazard assessment of the Italian territory. Tectonophysics 2008, 450, 85–108.
  61. Kaiser, A.; Balfour, N.; Fry, B.; Holden, C.; Litchfield, N.; Gerstenberger, M.; D’Anastasio, E.; Horspool, N.; McVerry, G.; Ristau, J.; et al. The 2016 Kaikōura, New Zealand, earthquake: Preliminary seismological report. Seismol. Res. Lett. 2017, 88, 727–739.
  62. Rhoades, D.A.; Christophersen, A. Time-varying probabilities of earthquake occurrence in central New Zealand based on the EEPAS model compensated for time-lag. Geophys. J. Int. 2019, 219, 417–429.
  63. Rastin, S.J.; Rhoades, D.A.; Rollins, C.; Gerstenberger, M.C.; Christophersen, A.; Thingbaijam, K.K.S. Spatial Distribution of Earthquake Occurrence for the New Zealand National Seismic Hazard Model Revision, GNS Science Report; SR2021-51; GNS Science: Lower Hutt, New Zealand, 2022.
  64. Rastin, S.J.; Rhoades, D.A.; Christophersen, A. Space–time trade-off of precursory seismicity in New Zealand and California revealed by a medium-term earthquake forecasting model. Appl. Sci. 2021, 11, 10215.
  65. Imoto, M.; Rhoades, D.A. Seismicity models of moderate earthquakes in Kanto, Japan utilizing multiple predictive parameters. Pure Appl. Geophys. 2010, 167, 831–843.
  66. Christophersen, A.; Rhoades, D.A.; Colella, H.V. Precursory seismicity in regions of low strain rate: Insights from a physics-based earthquake simulator. Geophys. J. Int. 2017, 209, 1513–1525.
  67. Rhoades, D.A.; Robinson, R.; Gerstenberger, M.C. Long-range predictability in physics-based synthetic earthquake catalogues. Geophys. J. Int. 2011, 185, 1037–1048.
  68. Richards-Dinger, K.; Dieterich, J.H. RSQSim Earthquake Simulator. Seismol. Res. Lett. 2012, 83, 983–990.
  69. Robinson, R.; Benites, R. Upgrading a synthetic seismicity model for more realistic fault ruptures. Geophys. Res. Lett. 2001, 28, 1843–1846.
  70. Scholz, C.H. The Mechanics of Earthquakes and Faulting, 3rd ed.; Cambridge University Press: Cambridge, UK, 2019.
  71. Rastin, S.J.; Rhoades, D.A.; Rollins, C.; Gerstenberger, M.C. How Useful Are Strain Rates for Estimating the Long-Term Spatial Distribution of Earthquakes? Appl. Sci. 2022, 12, 6804.
  72. Eberhart-Phillips, D.; Reyners, M.; Bannister, S.; Chadwick, M.; Ellis, S. Establishing a versatile 3-D seismic velocity model for New Zealand. Seismol. Res. Lett. 2010, 81, 992–1000.
  73. Havskov, J.; Ottemoller, L. Routine Data Processing in Earthquake Seismology: With Sample Data, Exercises and Software; Springer: Dordrecht, The Netherlands, 2010.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Geochemistry & Geophysics
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
David A. Rhoades
,
Sepideh J. Rastin
,
Annemarie Christophersen
View Times: 556
Revisions: 3 times (View History)
Update Date: 21 Oct 2022
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback