
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Sirius Huang | -- | 2110 | 2022-10-13 01:42:44 |
Video Upload Options
In chemistry, a steady state is a situation in which all state variables are constant in spite of ongoing processes that strive to change them. For an entire system to be at steady state, i.e. for all state variables of a system to be constant, there must be a flow through the system (compare mass balance). A simple example of such a system is the case of a bathtub with the tap running but with the drain unplugged: after a certain time, the water flows in and out at the same rate, so the water level (the state variable Volume) stabilizes and the system is in a steady state. The steady state concept is different from chemical equilibrium. Although both may create a situation where a concentration does not change, in a system at chemical equilibrium, the net reaction rate is zero (products transform into reactants at the same rate as reactants transform into products), while no such limitation exists in the steady state concept. Indeed, there does not have to be a reaction at all for a steady state to develop. The term steady state is also used to describe a situation where some, but not all, of the state variables of a system are constant. For such a steady state to develop, the system does not have to be a flow system. Therefore, such a steady state can develop in a closed system where a series of chemical reactions take place. Literature in chemical kinetics usually refers to this case, calling it steady state approximation. In simple systems the steady state is approached by state variables gradually decreasing or increasing until they reach their steady state value. In more complex systems state variable might fluctuate around the theoretical steady state either forever (a limit cycle) or gradually coming closer and closer. It theoretically takes an infinite time to reach steady state, just as it takes an infinite time to reach chemical equilibrium. Both concepts are, however, frequently used approximations because of the substantial mathematical simplifications these concepts offer. Whether or not these concepts can be used depends on the error the underlying assumptions introduce. So, even though a steady state, from a theoretical point of view, requires constant drivers (e.g. constant inflow rate and constant concentrations in the inflow), the error introduced by assuming steady state for a system with non-constant drivers may be negligible if the steady state is approached fast enough (relatively speaking).
1. Steady State Approximation in Chemical Kinetics
The steady state approximation,[1] occasionally called the stationary-state approximation or Bodenstein's quasi-steady state approximation, involves setting the rate of change of a reaction intermediate in a reaction mechanism equal to zero so that the kinetic equations can be simplified by setting the rate of formation of the intermediate equal to the rate of its destruction.
In practice it is sufficient that the rates of formation and destruction are approximately equal, which means that the net rate of variation of the concentration of the intermediate is small compared to the formation and destruction, and the concentration of the intermediate varies only slowly, similar to the reactants and products (see the equations and the green traces in the figures below).
Its use facilitates the resolution of the differential equations that arise from rate equations, which lack an analytical solution for most mechanisms beyond the simplest ones. The steady state approximation is applied, for example, in Michaelis-Menten kinetics.
As an example, the steady state approximation will be applied to two consecutive, irreversible, homogeneous first order reactions in a closed system. (For heterogeneous reactions, see reactions on surfaces.) This model corresponds, for example, to a series of nuclear decompositions like [math]\ce{ ^{239}U -> ^{239}Np -> ^{239}Pu\! }[/math].
If the rate constants for the following reaction are [math]\displaystyle{ k_1 }[/math] and [math]\displaystyle{ k_2 }[/math]; [math]\ce{ A -> B -> C }[/math], combining the rate equations with a mass balance for the system yields three coupled differential equations:
1.1. Reaction Rates
For species A: [math]\displaystyle{ \frac{d[\ce A]}{dt} = -k_1 [\ce A] }[/math]
For species B: [math]\displaystyle{ \frac{d[\ce B]}{dt} = k_1 [\ce A] - k_2 [\ce B] }[/math], Here the first (positive) term represents the formation of B by the first step [math]\ce{ A -> B }[/math], whose rate depends on the initial reactant A. The second (negative) term represents the consumption of B by the second step [math]\ce{ B -> C }[/math], whose rate depends on B as the reactant in that step.
For species C: [math]\displaystyle{ \frac{d[\ce C]}{dt} = k_2 [\ce B] }[/math], the rate of formation of C by the second step.
1.2. Analytical Solutions
The analytical solutions for these equations (supposing that initial concentrations of every substance except for A are zero) are:[2]
- [math]\displaystyle{ [\ce A]=[\ce A]_0 e^{-k_1 t} }[/math]
- [math]\displaystyle{ \left[ \ce B \right]= \begin{cases} \left[ \ce A \right]_{0}\frac{k_{1}}{k_{2}-k_{1}}\left( e^{-k_{1}t}-e^{-k_{2}t} \right);&k_{1}\ne k_{2} \\\\ \left[ \ce A \right]_{0}k_{1}te^{-k_{1}t};&k_{1} = k_{2} \\ \end{cases} }[/math]
- [math]\displaystyle{ \left[ \ce C \right]= \begin{cases} \left[ \ce A \right]_{0}\left( 1+\frac{k_{1}e^{-k_{2}t}-k_{2}e^{-k_{1}t}}{k_{2}-k_{1}} \right);&k_{1}\ne k_{2} \\\\ \left[ \ce A \right]_{0}\left( 1-e^{-k_{1}t}-k_{1}te^{-k_{1}t} \right);&k_{1} = k_{2} \\ \end{cases} }[/math]
1.3. Steady State
If the steady state approximation is applied, then the derivative of the concentration of the intermediate is set to zero. This reduces the second differential equation to an algebraic equation which is much easier to solve.
- [math]\displaystyle{ \frac{d[\ce B]}{dt} = 0 = k_1 [\ce A] - k_2 [\ce B] \Rightarrow \; [\ce B] = \frac{k_1}{k_2} [\ce A] }[/math].
Therefore, [math]\displaystyle{ \frac{d[\ce C]}{dt} = k_1 [\ce A] }[/math], so that [math]\displaystyle{ [\ce C]=[\ce A]_0 \left (1- e^{-k_1 t} \right ) }[/math].
Since [math]\displaystyle{ [\ce B] = \frac{k_1}{k_2} [\ce A] = \frac{k_1}{k_2}[\ce A]_0 e^{-k_1 t} }[/math], the concentration of the reaction intermediate B changes with the same time constant as [A] and is not in a steady state in that sense.
1.4. Validity
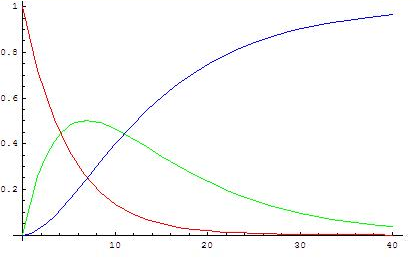
([math]\displaystyle{ k_2/k_1=0.5 }[/math])
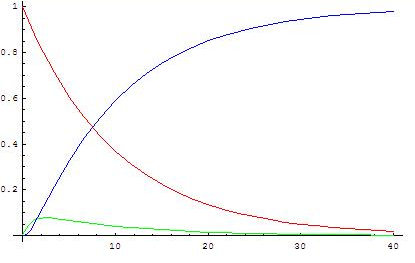
([math]\displaystyle{ k_2/k_1=10 }[/math])
The analytical and approximated solutions should now be compared in order to decide when it is valid to use the steady state approximation. The analytical solution transforms into the approximate one when [math]\displaystyle{ k_2 \gg k_1 }[/math], because then [math]\displaystyle{ e^{-k_2t} \ll e^{-k_1t} }[/math] and [math]\displaystyle{ k_2-k_1 \approx \; k_2 }[/math]. Therefore, it is valid to apply the steady state approximation only if the second reaction is much faster than the first (k2/k1 > 10 is a common criterion), because that means that the intermediate forms slowly and reacts readily so its concentration stays low.
The graphs show concentrations of A (red), B (green) and C (blue) in two cases, calculated from the analytical solution.
When the first reaction is faster it is not valid to assume that the variation of [B] is very small, because [B] is neither low or close to constant: first A transforms into B rapidly and B accumulates because it disappears slowly. As the concentration of A decreases its rate of transformation decreases, at the same time the rate of reaction of B into C increases as more B is formed, so a maximum is reached when [math]\displaystyle{ t=\begin{cases} \frac{\ln \left( \frac{k_{1}}{k_{2}} \right)}{k_{1}-k_{2}} & \, k_{1}\ne k_{2} \\\\ \frac{1}{k_{1}} & \, k_{1} = k_{2} \\ \end{cases} }[/math].
From then on the concentration of B decreases.
When the second reaction is faster, after a short induction period during which the steady state approximation does not apply, the concentration of B remains low (and more or less constant in an absolute sense) because its rates of formation and disappearance are almost equal and the steady state approximation can be used.
The equilibrium approximation can sometimes be used in chemical kinetics to yield similar results to the steady state approximation. It consists in assuming that the intermediate arrives rapidly at chemical equilibrium with the reactants. For example, Michaelis-Menten kinetics can be derived assuming equilibrium instead of steady state. Normally the requirements for applying the steady state approximation are laxer: the concentration of the intermediate is only needed to be low and more or less constant (as seen, this has to do only with the rates at which it appears and disappears) but it is not required to be at equilibrium.
2. Example
The reaction H2 + Br2 → 2 HBr has the following mechanism:
| Br2 → 2Br | k1 | Inititation |
| Br + H2 → HBr + H | k2 | Propagation |
| H + Br2 → HBr + Br | k3 | Propagation |
| H + HBr → H2 + Br | k4 | Inhibition |
| 2Br → Br2 | k5 | Breaking |
The rate of each species are:
[math]\displaystyle{ \frac{d[\ce HBr]}{dt} = k_2 [\ce Br] [\ce H_2] + k_3 [\ce H] [\ce Br_2] -k_4 [\ce H] [\ce HBr] }[/math]
[math]\displaystyle{ \frac{d[\ce H]}{dt} = k_2 [\ce Br] [\ce H_2] - k_3 [\ce H] [\ce Br_2] - k_4 [\ce H] [\ce HBr] }[/math]
[math]\displaystyle{ \frac{d[\ce Br]}{dt} = 2 k_1 [\ce Br_2] + k_3 [\ce H] [\ce Br_2] + k_4 [\ce H] [\ce HBr] - 2 k_5 [\ce Br]^2 }[/math]
[math]\displaystyle{ \frac{d[\ce Br_2]}{dt} = -k_1 [\ce Br_2] - k_3 [\ce H] [\ce Br_2] + k_5[\ce Br]^2 }[/math]
[math]\displaystyle{ \frac{d[\ce H_2]}{dt} = -k_2 [\ce Br] [\ce H_2] +k_4 [\ce H] [\ce HBr] }[/math]
These equations cannot be solved, because each one has values that change with time. For example, the first equation contains the concentrations of [Br], [H2] and [Br2], which depend on time, as can be seen in their respective equations.
To solve the rate equations the steady state approximation can be used. The reactants of this reaction are H2 and Br2, the intermediates are H and Br, and the product is HBr.
For solving the equations, the rates of the intermediates are set to 0 in the steady state approximation:
[math]\displaystyle{ \frac{d[\ce H]}{dt} = k_2 [\ce Br] [\ce H_2] -k_3 [\ce H] [\ce HBr]-k_4 [\ce H] [\ce HBr]=0 }[/math] → [math]\displaystyle{ k_2 [\ce Br] [\ce H_2]= k_3 [\ce H] [\ce HBr_2] }[/math]
[math]\displaystyle{ \frac{d[\ce Br]}{dt} = 2 k_1 [\ce Br_2] - k_2 [\ce Br] [\ce H_2] + k_3 [\ce H] [\ce Br_2] + k_4 [\ce H] [\ce HBr] - 2 k_5 [\ce Br]^2 }[/math]
From the reaction rate of H, k2 [Br][H2]-k3[H][Br2]-k4[H][HBr]= 0, so the reaction rate of Br can be simplified:
[math]\displaystyle{ 2 k_1 [\ce Br_2] - 2k_5 [\ce Br]^2 = 0 }[/math] → [math]\displaystyle{ [\ce Br] = \frac{k_1}{k_5}^\frac{1}{2} [\ce Br]^\frac{1}{2} }[/math]
[math]\displaystyle{ \frac{d[\ce HBr]}{dt} = k_2 [\ce Br] [\ce H_2] +k_3 [\ce H] [\ce Br_2] - k_4 [\ce H] [\ce HBr] }[/math]
[math]\displaystyle{ k_2 [\ce Br] [\ce H_2]-k_4 [\ce H] [\ce Br]= k_3 [\ce H] [\ce HBr_2] }[/math] → [math]\displaystyle{ \frac{d[\ce HBr]}{dt} =2k_3 [\ce H] [\ce Br_2] }[/math]
The reaction rate of HBr can also be simplifed, changing k2[Br][H2]-k4[H][Br] to k3[H][Br2], since both values are equal.
The concentration of H from equation 1 can be isolated:
[math]\displaystyle{ [\ce H]} = \frac{k_2 [\ce Br] [\ce H_2]}{k_3 [\ce Br_2]+k_4 [\ce H] [\ce HBr]} =\frac{k_2( \frac{k_1}{k_5}) ^ \frac{1}{2} [\ce Br_2] ^\frac{1}{2} [\ce H_2]} {{k_3 [\ce Br_2]+k_4 [\ce HBr]} }[/math]
The concentration of this intermediate is small and changes with time like the concentrations of reactants and product. It is inserted into the last differential equation to give
[math]\displaystyle{ \frac{d[\ce HBr]}{dt}=2k_3 [\ce H] [\ce Br_2]= 2k_3\left \lfloor \frac{k_2\left ( \frac{k_1}{k_5} \right ) ^ \frac{1}{2}[\ce Br_2]^ \frac{1}{2} [\ce H_2]}{k_3 [\ce Br_2]+k_4 [\ce HBr]} \right \rfloor [\ce Br_2] }[/math].
Simplifying the equation leads to
[math]\displaystyle{ \frac{d[\ce HBr]}{dt} =\frac{2k_3 k_2( \frac{k_1}{k_5}) ^ \frac{1}{2} [\ce Br_2] ^\frac{1}{2} [\ce H_2]} {{ k_3+\frac{k_4 [\ce HBr]}{[\ce Br_2]}}} }[/math].
The experimentally observed rate is
[math]\displaystyle{ v=\frac{k'[\ce H_2][\ce Br_2]^\tfrac{1}{2}}{1+k''\frac{[\ce HBr]}{ [\ce Br_2]}} }[/math].
The experimental rate law is very similar to the rate obtained with the steady state approximation, if k’ is 2k3k2(k1/k5)½ and 1+k’’ is k3+k4.
References
- IUPAC Gold Book definition of steady state http://goldbook.iupac.org/S05962.html
- P. W. Atkins and J. de Paula, Physical Chemistry (8th edition, W.H.Freeman 2006), p.811 ISBN:0-7167-8759-8





