1. ADI for Matrix Equations

1.1. The Method

The ADI method is a two step iteration process that alternately updates the column and row spaces of an approximate solution to [math]\displaystyle{ AX - XB = C }[/math]. One ADI iteration consists of the following steps:^[1]

1. Solve for [math]\displaystyle{ X^{(j + 1/2)} }[/math], where [math]\displaystyle{ \left( A - \beta_{j +1} I\right) X^{(j+1/2)} = X^{(j)}\left( B - \beta_{j + 1} I \right) + C. }[/math]

2. Solve for [math]\displaystyle{ X^{(j + 1)} }[/math], where [math]\displaystyle{ X^{(j+1)}\left( B - \alpha_{j + 1} I \right) = \left( A - \alpha_{j+1} I\right) X^{(j+1/2)} - C }[/math].

The numbers [math]\displaystyle{ (\alpha_{j+1}, \beta_{j+1}) }[/math] are called shift parameters, and convergence depends strongly on the choice of these parameters.^[2][3] To perform [math]\displaystyle{ K }[/math] iterations of ADI, an initial guess [math]\displaystyle{ X^{(0)} }[/math] is required, as well as [math]\displaystyle{ K }[/math] shift parameters, [math]\displaystyle{ \{ (\alpha_{j}, \beta_{j})\}_{j = 1}^{K} }[/math].

When to Use ADI

If [math]\displaystyle{ A \in \mathbb{C}^{m \times m} }[/math] and [math]\displaystyle{ B \in \mathbb{C}^{n \times n} }[/math], then [math]\displaystyle{ AX - XB = C }[/math] can be solved directly in [math]\displaystyle{ \mathcal{O}(m^3 + n^3) }[/math] using the Bartels-Stewart method.^[4] It is therefore only beneficial to use ADI when matrix-vector multiplication and linear solves involving [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] can be applied cheaply.

The equation [math]\displaystyle{ AX-XB=C }[/math] has a unique solution if and only if [math]\displaystyle{ \sigma(A) \cap \sigma(B) = \emptyset }[/math], where [math]\displaystyle{ \sigma(M) }[/math] is the spectrum of [math]\displaystyle{ M }[/math].^[5] However, the ADI method performs especially well when [math]\displaystyle{ \sigma(A) }[/math] and [math]\displaystyle{ \sigma(B) }[/math] are well-separated, and [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] are normal matrices. These assumptions are met, for example, by the Lyapunov equation [math]\displaystyle{ AX + XA^* = C }[/math] when [math]\displaystyle{ A }[/math] is positive definite. Under these assumptions, near-optimal shift parameters are known for several choices of [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math].^[2][3] Additionally, a priori error bounds can be computed, thereby eliminating the need to monitor the residual error in implementation.

The ADI method can still be applied when the above assumptions are not met. The use of suboptimal shift parameters may adversely affect convergence,^[5] and convergence is also affected by the non-normality of [math]\displaystyle{ A }[/math] or [math]\displaystyle{ B }[/math] (sometimes advantageously).^[6] Krylov subspace methods, such as the Rational Krylov Subspace Method,^[7] are observed to typically converge more rapidly than ADI in this setting,^[5][8] and this has led to the development of hybrid ADI-projection methods.^[8]

1.3. Shift Parameter Selection and the ADI Error Equation

The problem of finding good shift parameters is nontrivial. This problem can be understood by examining the ADI error equation. After [math]\displaystyle{ K }[/math] iterations, the error is given by

[math]\displaystyle{ X - X^{(K)} = \prod_{j = 1}^K \frac{(A - \alpha_j I)}{(A - \beta_j I)} \left ( X - X^{(0)} \right ) \prod_{j = 1}^K \frac{(B - \beta_j I)}{(B - \alpha_j I)}. }[/math]

Choosing [math]\displaystyle{ X^{(0)} = 0 }[/math] results in the following bound on the relative error:

[math]\displaystyle{ \frac{\left \|X - X^{(K)} \right \|_2}{\|X\|_2} \leq \| r_K(A) \|_2 \| r_K(B)^{-1}\|_2, \quad r_K(M) = \prod_{j = 1}^K \frac{(M - \alpha_j I)}{(M - \beta_j I)}. }[/math]

where [math]\displaystyle{ \| \cdot \|_2 }[/math] is the operator norm. The ideal set of shift parameters [math]\displaystyle{ \{ (\alpha_j, \beta_j)\}_{j = 1}^K }[/math] defines a rational function [math]\displaystyle{ r_K }[/math] that minimizes the quantity [math]\displaystyle{ \| r_K(A) \|_2 \| r_K(B)^{-1}\|_2 }[/math]. If [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] are normal matrices and have eigendecompositions [math]\displaystyle{ A = V_A\Lambda_AV_A^* }[/math] and [math]\displaystyle{ B = V_B\Lambda_BV_B^* }[/math], then

[math]\displaystyle{ \| r_K(A) \|_2 \| r_K(B)^{-1}\|_2 = \| r_K(\Lambda_A) \|_2 \| r_K(\Lambda_B)^{-1}\|_2 }[/math].

Near-optimal shift parameters

Near-optimal shift parameters are known in certain cases, such as when [math]\displaystyle{ \Lambda_A \subset [a, b] }[/math] and [math]\displaystyle{ \Lambda_B \subset [c, d] }[/math], where [math]\displaystyle{ [a, b] }[/math] and [math]\displaystyle{ [c, d] }[/math] are disjoint intervals on the real line.^[2][3] The Lyapunov equation [math]\displaystyle{ AX + XA^* = C }[/math], for example, satisfies these assumptions when [math]\displaystyle{ A }[/math] is positive definite. In this case, the shift parameters can be expressed in closed form using elliptic integrals, and can easily be computed numerically.

More generally, if closed, disjoint sets [math]\displaystyle{ E }[/math] and [math]\displaystyle{ F }[/math], where [math]\displaystyle{ \Lambda_A \subset E }[/math] and [math]\displaystyle{ \Lambda_B \subset F }[/math], are known, the optimal shift parameter selection problem is approximately solved by finding an extremal rational function that attains the value

[math]\displaystyle{ Z_K(E, F) : = \inf_{r} \frac{ \sup_{z \in E} |r(z)| }{ \inf_{z \in F} |r(z)| }, }[/math]

where the infimum is taken over all rational functions of degree [math]\displaystyle{ (K, K) }[/math].^[3] This approximation problem is related to several results in potential theory,^[9][10] and was solved by Zolotarev in 1877 for [math]\displaystyle{ E }[/math] = [a, b] and [math]\displaystyle{ F=-E. }[/math]^[11] The solution is also known when [math]\displaystyle{ E }[/math] and [math]\displaystyle{ F }[/math] are disjoint disks in the complex plane.^[12]

Heuristic shift parameter strategies

When less is known about [math]\displaystyle{ \sigma(A) }[/math] and [math]\displaystyle{ \sigma(B) }[/math], or when [math]\displaystyle{ A }[/math] or [math]\displaystyle{ B }[/math] are non-normal matrices, it may not be possible to find near-optimal shift parameters. In this setting, a variety of strategies for generating good shift parameters can be used. These include strategies based on asymptotic results in potential theory,^[13] using the Ritz values of the matrices [math]\displaystyle{ A }[/math], [math]\displaystyle{ A^{-1} }[/math], [math]\displaystyle{ B }[/math], and [math]\displaystyle{ B^{-1} }[/math] to formulate a greedy approach,^[14] and cyclic methods, where the same small collection of shift parameters are reused until a convergence tolerance is met.^[6][14] When the same shift parameter is used at every iteration, ADI is equivalent to an algorithm called Smith's method.^[15]

1.4. Factored ADI

In many applications, [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] are very large, sparse matrices, and [math]\displaystyle{ C }[/math] can be factored as [math]\displaystyle{ C = C_1C_2^* }[/math], where [math]\displaystyle{ C_1 \in \mathbb{C}^{m \times r}, C_2 \in \mathbb{C}^{n \times r} }[/math], with [math]\displaystyle{ r = 1, 2 }[/math].^[5] In such a setting, it may not be feasible to store the potentially dense matrix [math]\displaystyle{ X }[/math] explicitly. A variant of ADI, called factored ADI,^[8][16] can be used to compute [math]\displaystyle{ ZY^* }[/math], where [math]\displaystyle{ X \approx ZY^* }[/math]. The effectiveness of factored ADI depends on whether [math]\displaystyle{ X }[/math] is well-approximated by a low rank matrix. This is known to be true under various assumptions about [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math].^[3][6]

2. ADI for Parabolic Equations

Historically, the ADI method was developed to solve the 2D diffusion equation on a square domain using finite differences.^[17] Unlike ADI for matrix equations, ADI for parabolic equations does not require the selection of shift parameters, since the shift appearing in each iteration is determined by parameters such as the timestep, diffusion coefficient, and grid spacing. The connection to ADI on matrix equations can be observed when one considers the action of the ADI iteration on the system at steady state.

2.1. Example: 2D Diffusion Equation

Stencil figure for the alternating direction implicit method in finite difference equations. https://handwiki.org/wiki/index.php?curid=2088525

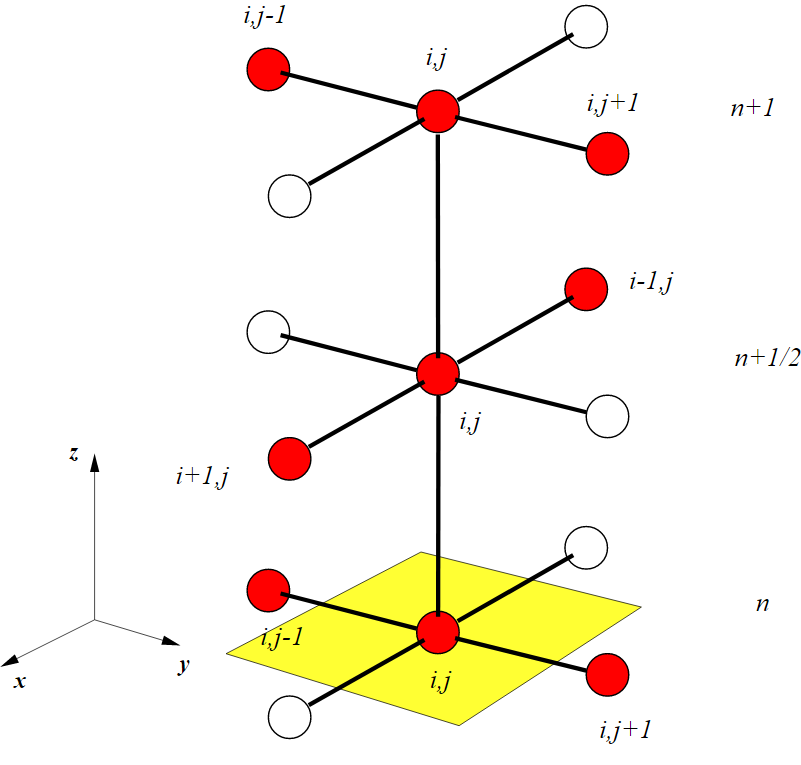
The traditional method for solving the heat conduction equation numerically is the Crank–Nicolson method. This method results in a very complicated set of equations in multiple dimensions, which are costly to solve. The advantage of the ADI method is that the equations that have to be solved in each step have a simpler structure and can be solved efficiently with the tridiagonal matrix algorithm.

Consider the linear diffusion equation in two dimensions,

[math]\displaystyle{ {\partial u\over \partial t} = \left({\partial^2 u\over \partial x^2 } + {\partial^2 u\over \partial y^2 } \right) = ( u_{xx} + u_{yy} ) }[/math]

The implicit Crank–Nicolson method produces the following finite difference equation:

[math]\displaystyle{ {u_{ij}^{n+1}-u_{ij}^n\over \Delta t} = {1 \over 2(\Delta x)^2}\left(\delta_x^2+\delta_y^2\right) \left(u_{ij}^{n+1}+u_{ij}^n\right) }[/math]

where:

[math]\displaystyle{ \Delta x = \Delta y }[/math]

and [math]\displaystyle{ \delta_p^2 }[/math] is the central second difference operator for the p-th coordinate

[math]\displaystyle{ \delta_p^2 u_{ij}=u_{ij+e_p}-2u_{ij}+u_{ij-e_p} }[/math]

with [math]\displaystyle{ e_p=10 }[/math] or [math]\displaystyle{ 01 }[/math] for [math]\displaystyle{ p=x }[/math] or [math]\displaystyle{ y }[/math] respectively (and [math]\displaystyle{ ij }[/math] a shorthand for lattice points [math]\displaystyle{ (i,j) }[/math]).

After performing a stability analysis, it can be shown that this method will be stable for any [math]\displaystyle{ \Delta t }[/math].

A disadvantage of the Crank–Nicolson method is that the matrix in the above equation is banded with a band width that is generally quite large. This makes direct solution of the system of linear equations quite costly (although efficient approximate solutions exist, for example use of the conjugate gradient method preconditioned with incomplete Cholesky factorization).

The idea behind the ADI method is to split the finite difference equations into two, one with the x-derivative taken implicitly and the next with the y-derivative taken implicitly,

[math]\displaystyle{ {u_{ij}^{n+1/2}-u_{ij}^n\over \Delta t/2} = {\left(\delta_x^2 u_{ij}^{n+1/2}+\delta_y^2 u_{ij}^{n}\right)\over \Delta x^2} }[/math]

[math]\displaystyle{ {u_{ij}^{n+1}-u_{ij}^{n+1/2}\over \Delta t/2} = {\left(\delta_x^2 u_{ij}^{n+1/2}+\delta_y^2 u_{ij}^{n+1}\right)\over \Delta y^2} }[/math]

The system of equations involved is symmetric and tridiagonal (banded with bandwidth 3), and is typically solved using tridiagonal matrix algorithm.

It can be shown that this method is unconditionally stable and second order in time and space.^[18] There are more refined ADI methods such as the methods of Douglas,^[19] or the f-factor method^[20] which can be used for three or more dimensions.

2.2. Generalizations

The usage of the ADI method as an operator splitting scheme can be generalized. That is, we may consider general evolution equations

[math]\displaystyle{ \dot u = F_1 u + F_2 u, }[/math]

where [math]\displaystyle{ F_1 }[/math] and [math]\displaystyle{ F_2 }[/math] are (possibly nonlinear) operators defined on a Banach space.^[21][22] In the diffusion example above we have [math]\displaystyle{ F_1 = {\partial^2 \over \partial x^2} }[/math] and [math]\displaystyle{ F_2 = {\partial^2 \over \partial y^2} }[/math].

3. Fundamental ADI (FADI)

3.1. Simplification of ADI to FADI

It is possible to simplify the conventional ADI method into Fundamental ADI method, which only has the similar operators at the left-hand sides while being operator-free at the right-hand sides. This may be regarded as the fundamental (basic) scheme of ADI method,^[23][24] with no more operator (to be reduced) at the right-hand sides, unlike most traditional implicit methods that usually consist of operators at both sides of equations. The FADI method leads to simpler, more concise and efficient update equations without degrading the accuracy of conventional ADI method.

3.2. Relations to Other Implicit Methods

Many classical implicit methods by Peachman-Rachford, Douglas-Gunn, D'Yakonov, Beam-Warming, Crank-Nicolson, etc., may be simplified to fundamental implicit schemes with operator-free right-hand sides.^[24] In their fundamental forms, the FADI method of second-order temporal accuracy can be related closely to the fundamental locally one-dimensional (FLOD) method, which can be upgraded to second-order temporal accuracy, such as for three-dimensional Maxwell's equations ^[25][26] in computational electromagnetics. For two- and three-dimensional heat conduction and diffusion equations, both FADI and FLOD methods may be implemented in simpler, more efficient and stable manner compared to their conventional methods. ^[27][28]