1. Oscillation Cases

Depending on the amount of damping present, a system exhibits different oscillatory behaviors.

• Where the spring–mass system is completely lossless, the mass would oscillate indefinitely, with each bounce of equal height to the last. This hypothetical case is called undamped.
• If the system contained high losses, for example if the spring–mass experiment were conducted in a viscous fluid, the mass could slowly return to its rest position without ever overshooting. This case is called overdamped.
• Commonly, the mass tends to overshoot its starting position, and then return, overshooting again. With each overshoot, some energy in the system is dissipated, and the oscillations die towards zero. This case is called underdamped.
• Between the overdamped and underdamped cases, there exists a certain level of damping at which the system will just fail to overshoot and will not make a single oscillation. This case is called critical damping. The key difference between critical damping and overdamping is that, in critical damping, the system returns to equilibrium in the minimum amount of time.

2. Definition

The effect of varying damping ratio on a second-order system.

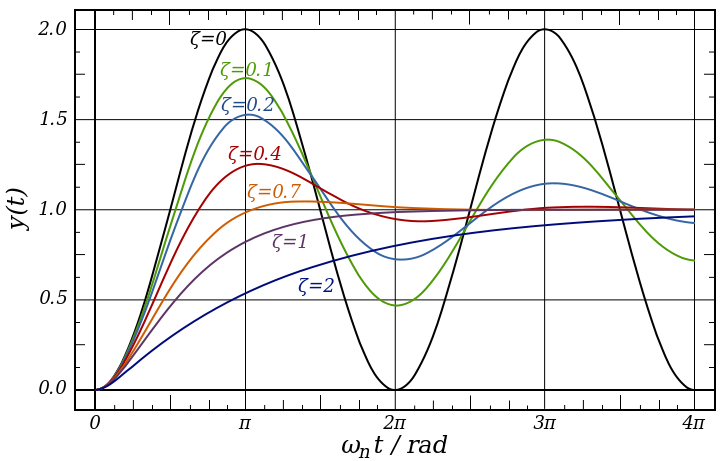
The damping ratio is a parameter, usually denoted by ζ (zeta),^[1] that characterizes the frequency response of a second-order ordinary differential equation. It is particularly important in the study of control theory. It is also important in the harmonic oscillator.

The damping ratio provides a mathematical means of expressing the level of damping in a system relative to critical damping. For a damped harmonic oscillator with mass m, damping coefficient c, and spring constant k, it can be defined as the ratio of the damping coefficient in the system's differential equation to the critical damping coefficient:

[math]\displaystyle{ \zeta = \frac{c}{c_c}, }[/math]

[math]\displaystyle{ \zeta = \frac {\text{actual damping}} {\text{critical damping}}, }[/math]

where the system's equation of motion is

[math]\displaystyle{ m\frac{d^2x}{dt^2} + c\frac{dx}{dt} + kx = 0 }[/math]

and the corresponding critical damping coefficient is

[math]\displaystyle{ c_c = 2 \sqrt{k m} }[/math]

or

[math]\displaystyle{ c_c = 2 m \sqrt{\frac{k}{m}} = 2m \omega_n }[/math]

where

[math]\displaystyle{ \omega_n = \sqrt{\frac{k}{m}} }[/math] is the natural frequency of the system.

The damping ratio is dimensionless, being the ratio of two coefficients of identical units.

3. Derivation

Using the natural frequency of a harmonic oscillator [math]\displaystyle{ \omega_n = \sqrt{\frac{k}{m}} }[/math] and the definition of the damping ratio above, we can rewrite this as:

[math]\displaystyle{ \frac{d^2x}{dt^2} + 2\zeta\omega_n\frac{dx}{dt} + \omega_n^2 x = 0. }[/math]

This equation can be solved with the approach.

[math]\displaystyle{ x(t) = C e^{s t},\, }[/math]

where C and s are both complex constants, with s satisfying

[math]\displaystyle{ s = -\omega_n \left(\zeta \pm i \sqrt{1 - \zeta^2}\right). }[/math]

Two such solutions, for the two values of s satisfying the equation, can be combined to make the general real solutions, with oscillatory and decaying properties in several regimes:

Undamped

Is the case where [math]\displaystyle{ \zeta = 0 }[/math] corresponds to the undamped simple harmonic oscillator, and in that case the solution looks like [math]\displaystyle{ \exp(i\omega_nt) }[/math], as expected.

Underdamped

If s is a pair of complex values, then each complex solution term is a decaying exponential combined with an oscillatory portion that looks like [math]\displaystyle{ \exp\left(i \omega_n \sqrt{1 - \zeta^2}t\right) }[/math]. This case occurs for [math]\displaystyle{ \ 0 \le \zeta \lt 1 }[/math], and is referred to as underdamped.

Overdamped

If s is a pair of real values, then the solution is simply a sum of two decaying exponentials with no oscillation. This case occurs for [math]\displaystyle{ \zeta \gt 1 }[/math], and is referred to as overdamped.

Critically damped

The case where [math]\displaystyle{ \zeta = 1 }[/math] is the border between the overdamped and underdamped cases, and is referred to as critically damped. This turns out to be a desirable outcome in many cases where engineering design of a damped oscillator is required (e.g., a door closing mechanism).

4. Q Factor and Decay Rate

The Q factor, damping ratio ζ, and exponential decay rate α are related such that^[2]

[math]\displaystyle{ \zeta = \frac{1}{2 Q} = { \alpha \over \omega_n }. }[/math]

When a second-order system has [math]\displaystyle{ \zeta \lt 1 }[/math] (that is, when the system is underdamped), it has two complex conjugate poles that each have a real part of [math]\displaystyle{ -\alpha }[/math]; that is, the decay rate parameter [math]\displaystyle{ \alpha }[/math] represents the rate of exponential decay of the oscillations. A lower damping ratio implies a lower decay rate, and so very underdamped systems oscillate for long times.^[3] For example, a high quality tuning fork, which has a very low damping ratio, has an oscillation that lasts a long time, decaying very slowly after being struck by a hammer.

5. Logarithmic Decrement

For underdamped vibrations, the damping ratio is also related to the logarithmic decrement [math]\displaystyle{ \delta }[/math] via the relation

[math]\displaystyle{ \zeta = \frac{1}{\sqrt{1 + \left(\frac{2\pi}{\delta}\right)^2}} \qquad \text{where} \qquad \delta \triangleq \ln\frac{x_1}{x_2} }[/math]

where [math]\displaystyle{ x_1 }[/math] and [math]\displaystyle{ x_2 }[/math] are the vibration amplitudes at two successive peaks of the decaying vibration.

6. Percentage Overshoot

In control theory, overshoot refers to an output exceeding its final, steady-state value.^[4] For a step input, the percentage overshoot (PO) is the maximum value minus the step value divided by the step value. In the case of the unit step, the overshoot is just the maximum value of the step response minus one.

The percentage overshoot (PO) is related to damping ratio (ζ) by:

[math]\displaystyle{ PO = 100 e^{-\left(\frac{\zeta\pi}{\sqrt{1-\zeta^2}}\right)} }[/math]

Conversely, the damping ratio (ζ) that yields a specific percent overshoot (PO) is given by:

[math]\displaystyle{ \zeta = \frac{-\ln\left(\frac{PO}{100}\right)}{\sqrt{\pi^2 + \ln^2\left(\frac{PO}{100}\right)}} }[/math]