1. Details

Plot of a two-dimensional slice of the gravitational potential in and around a uniformly dense, spherically symmetric body. By AllenMcC. - This diagram was created with Mathematica., CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=3871594

This image shows the four trajectory categories with the gravitational potential well (gravity well) of the central mass's field of potential energy shown in black and the height of the kinetic energy of the moving body shown in red extending above that, correlating to changes in speed as distance changes according to Kepler's laws. By Invent2HelpAll - http://preview.tinyurl{dot}com/Thesis-EnergyPotentialAnalysis - Figure 3.2 on pdf pg34of64., CC0, https://commons.wikimedia.org/w/index.php?curid=19436084

This image shows how the gravitational force vector field is inter-related with the gravity well. This shows how it is only a 2‑dimensional slice of the gravity field that is represented in the gravity well. The z axis is no longer a spatial dimension, but now represents energy.

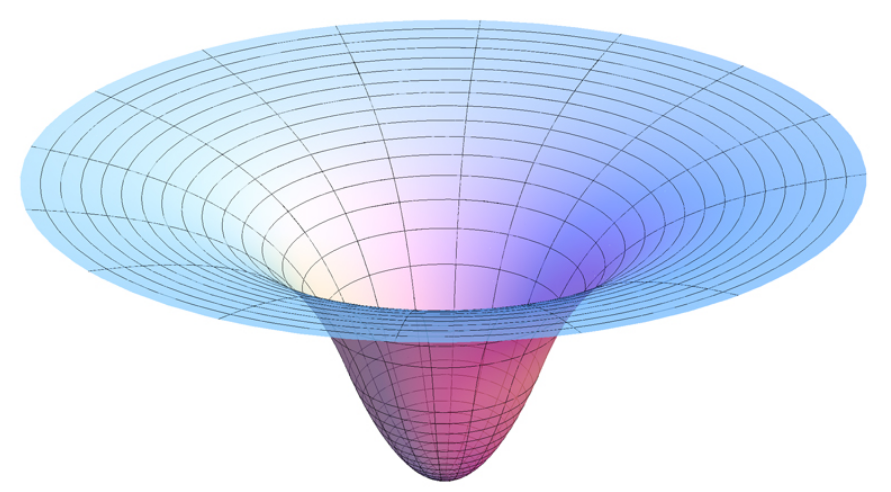
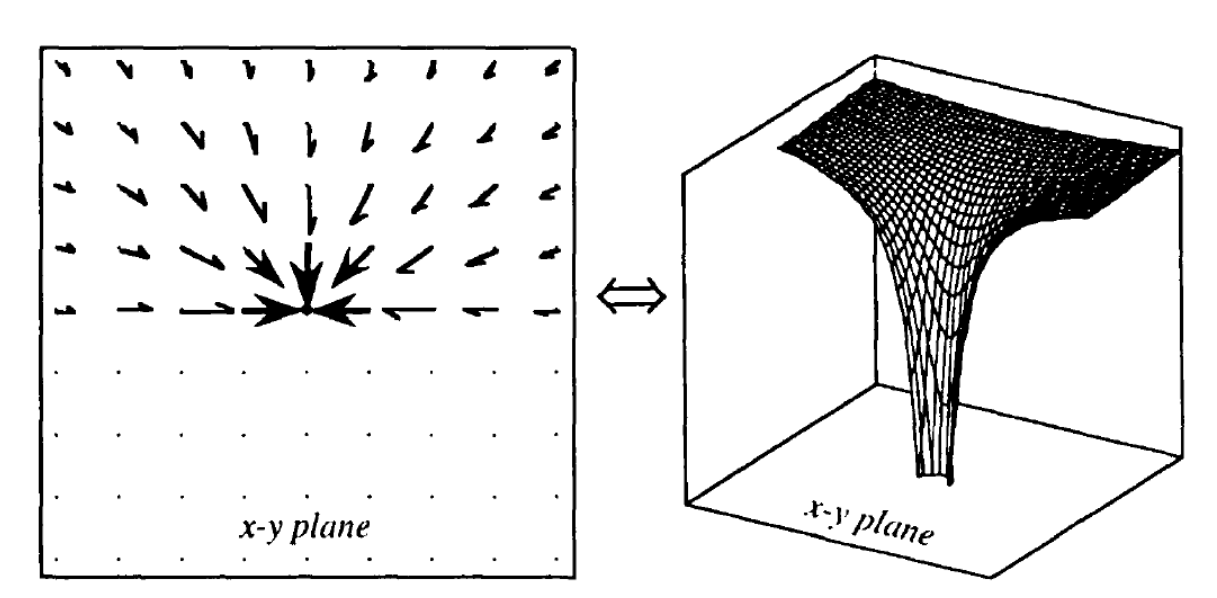
If G is the universal gravitational constant (G = 6.67×10⁻¹¹ m³ kg⁻¹ s⁻²), the external gravitational potential of a spherically symmetric body of mass M at the location described by the displacement vector [math]\displaystyle{ \mathbf{x} }[/math] from the center of mass of the body, is given by the formula:

[math]\displaystyle{ \Phi(\mathbf{x}) = -\frac{GM}{|\mathbf{x}|}. }[/math]

A plot of this function in two dimensions is shown in the figure. This plot has been completed with an interior potential proportional to |x|², corresponding to an object of uniform density, but this interior potential is generally irrelevant since the orbit of a test particle cannot intersect the body.

The potential function has a hyperbolic cross section; the sudden dip in the center is the origin of the name "gravity well". A black hole would not have this "closing" dip due to its size being only determined by its event horizon.

2. Physical Gravity Wells

In a uniform gravitational field, the gravitational potential at a point is proportional to the height. Thus if the graph of a gravitational potential Φ(x,y) is constructed as a physical surface and placed in a uniform gravitational field so that the actual field points in the −Φ direction, then each point on the surface will have an actual gravitational potential proportional to the value of Φ at that point. As a result, an object constrained to move on the surface will have roughly the same equation of motion as an object moving in the potential field Φ itself. Gravity wells constructed on this principle can be found in many science museums.

There are several sources of inaccuracy in this model:

• The friction between the object and the surface has no analogue in vacuum. This effect can be reduced by using a rolling ball instead of a sliding block.
• The object's vertical motion contributes kinetic energy which has no analogue. This effect can be reduced by making the gravity well shallower (i.e. by choosing a smaller scaling factor for the Φ axis).
• A rolling ball's rotational kinetic energy has no analogue. This effect can be reduced by concentrating the ball's mass near its center so that the moment of inertia is small compared to mr².
• A ball's center of mass is not located on the surface but at a fixed distance r, which changes its potential energy by an amount depending on the slope of the surface at that point. For balls of a fixed size, this effect can be eliminated by constructing the surface so that the center of the ball, rather than the surface itself, lies on the graph of Φ.

3. The Rubber-Sheet Model

Consider an idealized rubber sheet suspended in a uniform gravitational field normal to the sheet. In equilibrium, the elastic tension in each part of the sheet must be equal and opposite to the gravitational pull on that part of the sheet; that is,

[math]\displaystyle{ k \nabla^2 h = g \rho }[/math]

where k is the elastic constant of the rubber, h(x) is the upward displacement of the sheet (assumed to be small), g is the strength of the gravitational field, and ρ(x) is the mass density of the sheet. The mass density may be viewed as intrinsic to the sheet or as belonging to objects resting on top of the sheet. This equilibrium condition is identical in form to the gravitational Poisson equation

[math]\displaystyle{ \nabla^2 \Phi = 4 \pi G \rho }[/math]

where Φ(x) is the gravitational potential and ρ(x) is the mass density. Thus a massive object placed on a rubber sheet will deform the sheet into a shape, that, to a first approximation, depicts correctly the gravity well in 2-dimensional space (not correctly, however, for 3-dimensional space). A second test object placed near the first will gravitate toward it in an approximation of the correct force law.

4. Gravity Wells and General Relativity

A type of embedding diagram that depicts general relativity's curvature of space. Although analogous, this does not depict the Sun's gravity well. 

Both the rigid gravity well and the rubber-sheet model are frequently misidentified as models of general relativity due to an accidental resemblance to general relativistic embedding diagrams, and perhaps Einstein's employment of gravitational "curvature" bending the path of light he described as a prediction of general relativity. The embedding diagram most commonly found in textbooks, an isometric embedding of a constant-time equatorial slice of the Schwarzschild metric in Euclidean 3-dimensional space, superficially resembles a gravity well. However, embedding diagrams fundamentally differ from gravity wells.

Embedding takes merely a shape, but a potential plot has a distinguished "downward" direction. Turning a gravity well "upside down" by negating the potential of the attractive force, turns it into a repulsive force. However, turning a Schwarzschild embedding upside down, by rotating it, has no effect, since it leaves its intrinsic geometry unchanged. Also, geodesics following across the Schwarzschild surface would bend toward the central mass like a ball rolling in a gravity well, but for entirely different reasons. There is no analogy of the Schwarzschild embedding for a repulsive field though such a field is modeled in general relativity, the spatial geometry cannot be embedded in three dimensions.

The Schwarzschild embedding is commonly drawn with a hyperbolic cross section like the potential well, but in fact it has a parabolic cross section which, unlike the gravity well, does not approach a planar asymptote. See Flamm's paraboloid.