1. Definition

1.1. Non-Symmetric Operad

A non-symmetric operad (sometimes called an operad without permutations, or a non-[math]\displaystyle{ \Sigma }[/math] or plain operad) consists of the following:

• a sequence [math]\displaystyle{ (P(n))_{n\in\mathbb{N}} }[/math] of sets, whose elements are called [math]\displaystyle{ n }[/math]-ary operations,
• an element [math]\displaystyle{ 1 }[/math] in [math]\displaystyle{ P(1) }[/math] called the identity,
• for all positive integers [math]\displaystyle{ n }[/math], [math]\displaystyle{ k_1,\ldots,k_n }[/math], a composition function

[math]\displaystyle{ \begin{align} \circ: P(n)\times P(k_1)\times\cdots\times P(k_n) & \to P(k_1+\cdots+k_n)\\ (\theta,\theta_1,\ldots,\theta_n) & \mapsto \theta\circ(\theta_1,\ldots,\theta_n), \end{align} }[/math]

satisfying the following coherence axioms:

• identity: [math]\displaystyle{ \theta\circ(1,\ldots,1)=\theta=1\circ\theta }[/math]
• associativity:

[math]\displaystyle{ \begin{align} & \theta \circ (\theta_1 \circ (\theta_{1,1}, \ldots, \theta_{1,k_1}), \ldots, \theta_n \circ (\theta_{n,1}, \ldots,\theta_{n,k_n})) \\ = {} & (\theta \circ (\theta_1, \ldots, \theta_n)) \circ (\theta_{1,1}, \ldots, \theta_{1,k_1}, \ldots, \theta_{n,1}, \ldots, \theta_{n,k_n}) \end{align} }[/math]

(the number of arguments corresponds to the arities of the operations).

Alternatively, a plain operad is a multicategory with one object.

1.2. Symmetric Operad

A Operad Theorya non-symmetric operad [math]\displaystyle{ P }[/math] as above, together with a right action of the symmetric group [math]\displaystyle{ \Sigma_n }[/math] on [math]\displaystyle{ P(n) }[/math], satisfying the above associative and identity axioms, as well as

• equivariance: given permutations [math]\displaystyle{ s_i \in \Sigma_{k_i}, t\in \Sigma_n }[/math],

[math]\displaystyle{ \begin{align} & (\theta*t)\circ(\theta_{t1},\ldots,\theta_{tn}) = (\theta\circ(\theta_1,\ldots,\theta_n))*t; \\[2pt] & \theta\circ(\theta_1*s_1,\ldots,\theta_n*s_n) = (\theta\circ(\theta_1,\ldots,\theta_n))*(s_1,\ldots,s_n) \end{align} }[/math]

(where by abuse of notation, [math]\displaystyle{ t }[/math] on the right hand side of the first equivariance relation is the element of [math]\displaystyle{ \Sigma_{k_1+\dots+k_n} }[/math] that acts on the set [math]\displaystyle{ \{1, 2, \dots , k_1+\dots +k_n\} }[/math] by breaking it into [math]\displaystyle{ n }[/math] blocks, the first of size [math]\displaystyle{ k_1 }[/math], the second of size [math]\displaystyle{ k_2 }[/math], through the [math]\displaystyle{ n }[/math]th block of size [math]\displaystyle{ k_n }[/math], and then permutes these [math]\displaystyle{ n }[/math] blocks by [math]\displaystyle{ t }[/math]).

The permutation actions in this definition are vital to most applications, including the original application to loop spaces.

1.3. Morphisms

A morphism of operads [math]\displaystyle{ f:P\to Q }[/math] consists of a sequence

[math]\displaystyle{ (f_n:P(n)\to Q(n))_{n\in\mathbb{N}} }[/math]

which:

• preserves the identity: [math]\displaystyle{ f(1)=1 }[/math]
• preserves composition: for every n-ary operation [math]\displaystyle{ \theta }[/math] and operations [math]\displaystyle{ \theta_1 , \ldots , \theta_n }[/math],

[math]\displaystyle{ f(\theta\circ(\theta_1,\ldots,\theta_n)) = f(\theta)\circ(f(\theta_1),\ldots,f(\theta_n)) }[/math]

• preserves the permutation actions: [math]\displaystyle{ f(x*s)=f(x)*s }[/math].

1.4. In Other Categories

We have so far considered only operads in the category of sets. It is actually possible to define operads in any symmetric monoidal category (or, for non-symmetric operads, any monoidal category).

A common example would be given by the category of topological space, with the monoidal product given by the Cartesian product. In this case, a topological operad is given by a sequence of spaces (instead of sets) [math]\displaystyle{ \{ P(n) \}_{n \ge 0} }[/math]. The structure maps of the operad (the composition and the actions of the symmetric groups) must then be assumed to be continuous. The result is called a topological operad. Similarly, in the definition of a morphism, it would be necessary to assume that the maps involved are continuous.

Other common settings to define operads include, for example, module over a ring, chain complexes, groupoids (or even the category of categories itself), coalgebras, etc.

2. Understanding the Axioms

2.1. Associativity Axiom

"Associativity" means that composition of operations is associative (the function [math]\displaystyle{ \circ }[/math] is associative), analogous to the axiom in category theory that [math]\displaystyle{ f \circ (g \circ h) = (f \circ g) \circ h }[/math]; it does not mean that the operations themselves are associative as operations. Compare with the associative operad, below.

Associativity in operad theory means that one can write expressions involving operations without ambiguity from the omitted compositions, just as associativity for operations allows one to write products without ambiguity from the omitted parentheses.

For instance, suppose that [math]\displaystyle{ \theta }[/math] is a binary operation, which is written as [math]\displaystyle{ \theta(a,b) }[/math] or [math]\displaystyle{ (ab) }[/math]. Note that [math]\displaystyle{ \theta }[/math] may or may not be associative.

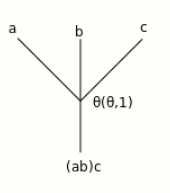
Then what is commonly written [math]\displaystyle{ ((ab)c) }[/math] is unambiguously written operadically as [math]\displaystyle{ \theta \circ (\theta,1) }[/math] . This sends [math]\displaystyle{ (a,b,c) }[/math] to [math]\displaystyle{ (ab,c) }[/math] (apply [math]\displaystyle{ \theta }[/math] on the first two, and the identity on the third), and then the [math]\displaystyle{ \theta }[/math] on the left "multiplies" [math]\displaystyle{ ab }[/math] by [math]\displaystyle{ c }[/math]. This is clearer when depicted as a tree:

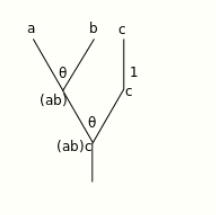
By Michiexile at English Wikipedia, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=24465042

which yields a 3-ary operation:

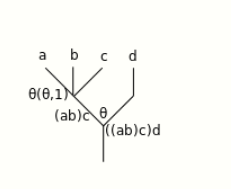
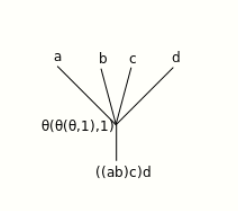
However, the expression [math]\displaystyle{ (((ab)c)d) }[/math] is a priori ambiguous: it could mean [math]\displaystyle{ \theta \circ ((\theta,1) \circ ((\theta,1),1)) }[/math], if the inner compositions are performed first, or it could mean [math]\displaystyle{ (\theta \circ (\theta,1)) \circ ((\theta,1),1) }[/math], if the outer compositions are performed first (operations are read from right to left). Writing [math]\displaystyle{ x=\theta, y=(\theta,1), z=((\theta,1),1) }[/math], this is [math]\displaystyle{ x \circ (y \circ z) }[/math] versus [math]\displaystyle{ (x \circ y) \circ z }[/math]. That is, the tree is missing "vertical parentheses":

By Michiexile at English Wikipedia, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=24465052

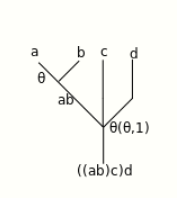
If the top two rows of operations are composed first (puts an upward parenthesis at the [math]\displaystyle{ (ab)c\ \ d }[/math] line; does the inner composition first), the following results:

By Michiexile at English Wikipedia, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=24465073

which then evaluates unambiguously to yield a 4-ary operation. As an annotated expression:

[math]\displaystyle{ \theta_{(ab)c\cdot d} \circ ((\theta_{ab \cdot c},1_d) \circ ((\theta_{a\cdot b},1_c),1_d)) }[/math]

By Michiexile at English Wikipedia, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=24465068

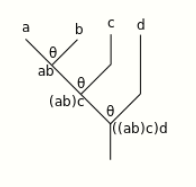
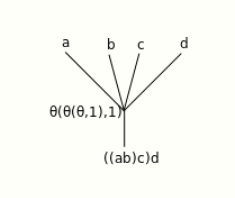
If the bottom two rows of operations are composed first (puts a downward parenthesis at the [math]\displaystyle{ ab\quad c\ \ d }[/math] line; does the outer composition first), following results:

By Michiexile at English Wikipedia, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=24465062

which then evaluates unambiguously to yield a 4-ary operation:

By Michiexile at English Wikipedia, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=24465068

The operad axiom of associativity is that these yield the same result, and thus that the expression [math]\displaystyle{ (((ab)c)d) }[/math] is unambiguous. 

2.2. Identity Axiom

The identity axiom (for a binary operation) can be visualized in a tree as:

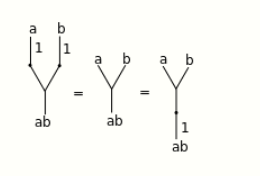
By Michiexile at English Wikipedia, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=24465005

meaning that the three operations obtained are equal: pre- or post- composing with the identity makes no difference. Note that, as for categories, [math]\displaystyle{ 1 \circ 1 = 1 }[/math] is a corollary of the identity axiom. 

3. Examples

Operadic composition in the little 2-discs operad. By Ladislav_the_Posthumous (talk) (Uploads) - Own work, CC BY-SA 3.0, https://en.wikipedia.org/w/index.php?curid=13907966

Operadic composition in the operad of symmetries. By Ladislav the Posthumous at English Wikipedia, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=24465003

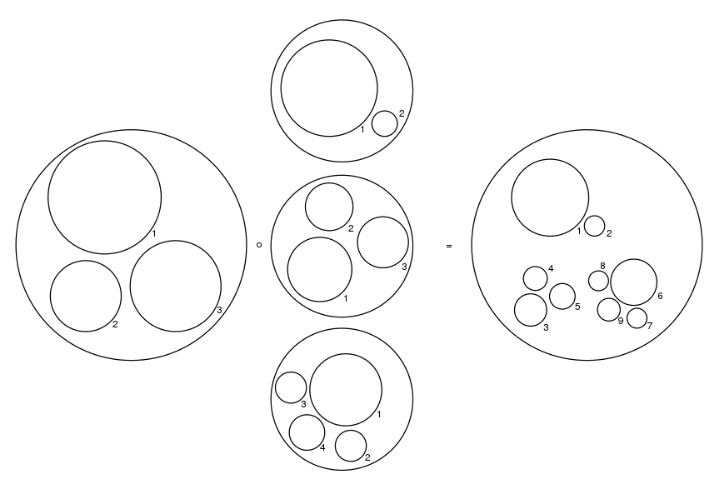
3.1. "Little Something" Operads

A little discs operad or, little balls operad or, more specifically, the little n-discs operad is a topological operad defined in terms of configurations of disjoint n-dimensional discs inside a unit n-disc centered in the origin of Rⁿ. The operadic composition for little 2-discs is illustrated in the figure.^[1]

Originally the little n-cubes operad or the little intervals operad (initially called little n-cubes PROPs) was defined by Michael Boardman and Rainer Vogt in a similar way, in terms of configurations of disjoint axis-aligned n-dimensional hypercubes (n-dimensional intervals) inside the unit hypercube.^[2] Later it was generalized by May^[3] to little convex bodies operad, and "little discs" is a case of "folklore" derived from the "little convex bodies".^[4]

3.2. Associative Operad

Another class of examples of operads are those capturing the structures of algebraic structures, such as associative algebras, commutative algebras and Lie algebras. Each of these can be exhibited as a finitely presented operad, in each of these three generated by binary operations.

Thus, the associative operad is generated by a binary operation [math]\displaystyle{ \psi }[/math], subject to the condition that

[math]\displaystyle{ \psi\circ(\psi,1)=\psi\circ(1,\psi). }[/math]

This condition does correspond to associativity of the binary operation [math]\displaystyle{ \psi }[/math]; writing [math]\displaystyle{ \psi(a,b) }[/math] multiplicatively, the above condition is [math]\displaystyle{ (ab)c = a(bc) }[/math]. This associativity of the operation should not be confused with associativity of composition; see the axiom of associativity, above.

This operad is terminal in the category of non-symmetric operads, as it has exactly one n-ary operation for each n, corresponding to the unambiguous product of n terms: [math]\displaystyle{ x_1 \dotsb x_n }[/math]. For this reason, it is sometimes written as 1 by category theorists (by analogy with the one-point set, which is terminal in the category of sets).

3.3. Terminal Symmetric Operad

The terminal symmetric operad is the operad whose algebras are commutative monoids, which also has one n-ary operation for each n, with each [math]\displaystyle{ S_n }[/math] acting trivially; this triviality corresponds to commutativity, and whose n-ary operation is the unambiguous product of n-terms, where order does not matter:

[math]\displaystyle{ x_1 \dotsb x_n = x_{\sigma(1)} \dotsb x_{\sigma(n)} }[/math]

for any permutation [math]\displaystyle{ \sigma \in S_n }[/math].

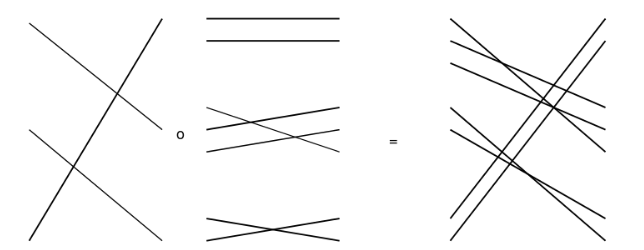
3.4. Operads from the Symmetric and Braid Groups

There is an operad for which each [math]\displaystyle{ P(n) }[/math] is given by the symmetric group [math]\displaystyle{ S_n }[/math]. The composite [math]\displaystyle{ \sigma \circ (\tau_1, \dots, \tau_n) }[/math] permutes its inputs in blocks according to [math]\displaystyle{ \sigma }[/math], and within blocks according to the appropriate [math]\displaystyle{ \tau_i }[/math]. Similarly, there is a non-[math]\displaystyle{ \Sigma }[/math] operad for which each [math]\displaystyle{ P(n) }[/math] is given by the Artin braid group [math]\displaystyle{ B_n }[/math]. Moreover, this non-[math]\displaystyle{ \Sigma }[/math] operad has the structure of a braided operad, which generalizes the notion of an operad from symmetric to braid groups.

3.5. Linear Algebra

In linear algebra, one can consider vector spaces to be algebras over the operad [math]\displaystyle{ \mathbf{R}^\infty }[/math] (the infinite direct sum, so only finitely many terms are non-zero; this corresponds to only taking finite sums), which parametrizes linear combinations: the vector [math]\displaystyle{ (2,3,-5,0,\dots) }[/math] for instance corresponds to the linear combination

[math]\displaystyle{ 2v_1 + 3v_2 -5v_3 + 0v_4 + \cdots. }[/math]

Similarly, one can consider affine combinations, conical combinations, and convex combinations to correspond to the sub-operads where the terms sum to 1, the terms are all non-negative, or both, respectively. Graphically, these are the infinite affine hyperplane, the infinite hyper-octant, and the infinite simplex. This formalizes what is meant by [math]\displaystyle{ \mathbf{R}^n }[/math] being or the standard simplex being model spaces, and such observations as that every bounded convex polytope is the image of a simplex. Here suboperads correspond to more restricted operations and thus more general theories.

This point of view formalizes the notion that linear combinations are the most general sort of operation on a vector space – saying that a vector space is an algebra over the operad of linear combinations is precisely the statement that all possible algebraic operations in a vector space are linear combinations. The basic operations of vector addition and scalar multiplication are a generating set for the operad of all linear combinations, while the linear combinations operad canonically encodes all possible operations on a vector space.