1. Hyperboloid and Klein Models
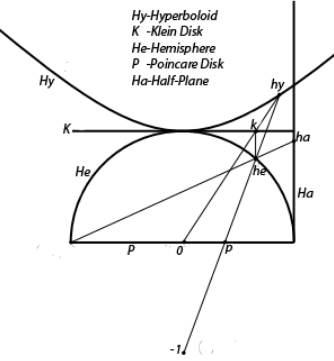
Geometric relations between Poincaré disk model, hyperboloid model and Klein model.
In this section two different models are given for hyperbolic geometry on the unit disk or equivalently the upper half plane.[1]
The group G = SU(1,1) is formed of matrices
- [math]\displaystyle{ g = \begin{pmatrix} \alpha & \beta \\ \overline{\beta} & \overline{\alpha}\end{pmatrix} }[/math]
with
- [math]\displaystyle{ |\alpha|^2 -|\beta|^2=1. }[/math]
It is a subgroup of Gc = SL(2,C), the group of complex 2 × 2 matrices with determinant 1. The group Gc acts by Möbius transformations on the extended complex plane. The subgroup G acts as automorphisms of the unit disk D and the subgroup G1 = SL(2,R) acts as automorphisms of the upper half plane. If
- [math]\displaystyle{ C=\begin{pmatrix}1 & i \\ i & 1\end{pmatrix} }[/math]
then
- [math]\displaystyle{ G=CG_1C^{-1}, }[/math]
since the Möbius transformation corresponding M is the Cayley transform carrying the upper half plane onto the unit disk and the real line onto the unit circle.
The Lie algebra [math]\displaystyle{ \mathfrak{g} }[/math] of SU(1,1) consists of matrices
- [math]\displaystyle{ X= \begin{pmatrix} ix & w \\ \overline{w} & -ix \end{pmatrix} }[/math]
with x real. Note that X2 = (|w|2 – x2) I and
- [math]\displaystyle{ \det X = x^2 -|w|^2 =-\tfrac12 \operatorname{Tr} X^2. }[/math]
The hyperboloid [math]\displaystyle{ \mathfrak{H} }[/math] in [math]\displaystyle{ \mathfrak{g} }[/math] is defined by two conditions. The first is that det X = 1 or equivalently Tr X2 = –2. By definition this condition is preserved under conjugation by G. Since G is connected it leaves the two components with x > 0 and x < 0 invariant. The second condition is that x > 0. For brevity, write X = (x,w).
The group G acts transitively on D and [math]\displaystyle{ \mathfrak{H} }[/math] and the points 0 and (1,0) have stabiliser K consisting of matrices
- [math]\displaystyle{ \begin{pmatrix}\zeta & 0 \\ 0 & \overline{\zeta}\end{pmatrix} }[/math]
with |ζ| = 1. Polar decomposition on D implies the Cartan decomposition G = KAK where A is the group of matrices
- [math]\displaystyle{ a_t = \begin{pmatrix}\cosh t & \sinh t \\ \sinh t & \cosh t\end{pmatrix}. }[/math]
Both spaces can therefore be identified with the homogeneous space G/K and there is a G-equivariant map f of [math]\displaystyle{ \mathfrak{H} }[/math] onto D sending (1,0) to 0. To work out the formula for this map and its inverse it suffices to compute g(1,0) and g(0) where g is as above. Thus g(0) = β/α and
- [math]\displaystyle{ g(1,0)=(|\alpha|^2 +|\beta|^2,-2i\alpha\beta), }[/math]
so that
- recovering the formula
- [math]\displaystyle{ f(x,w) = \frac{iw}{x + 1}. }[/math]
Conversely if z = iw/(x + 1), then |z|2 = (x – 1)/(x + 1), giving the inverse formula
- [math]\displaystyle{ f^{-1}(z) = (x,w) = \left( \frac{1 + |z|{}^2}{1 - |z|{}^2}, \frac{-2iz}{1 - |z|{}^2} \right). }[/math]
This correspondence extends to one between geometric properties of D and [math]\displaystyle{ \mathfrak{H} }[/math]. Without entering into the correspondence of G-invariant Riemannian metrics,[2] each geodesic circle in D corresponds to the intersection of 2-planes through the origin, given by equations Tr XY = 0, with [math]\displaystyle{ \mathfrak{H} }[/math]. Indeed, this is obvious for rays arg z = θ through the origin in D—which correspond to the 2-planes arg w = θ—and follows in general by G-equivariance.
The Klein model is obtained by using the map F(x,w) = w/x as the correspondence between [math]\displaystyle{ \mathfrak{H} }[/math] and D. Identifying this disk with (1,v) with |v| < 1, intersections of 2-planes with [math]\displaystyle{ \mathfrak{H} }[/math] correspond to intersections of the same 2-planes with this disk and so give straight lines. The Poincaré-Klein map given by
- [math]\displaystyle{ K(z) = iF \circ f^{-1}(z) = \frac{2z}{1 + |z|{}^2} }[/math]
thus gives a diffeomorphism from the unit disk onto itself such that Poincaré geodesic circles are carried into straight lines. This diffeomorphism does not preserve angles but preserves orientation and, like all diffeomorphisms, takes smooth curves through a point making an angle less than π (measured anticlockwise) into a similar pair of curves.[3] In the limiting case, when the angle is π, the curves are tangent and this again is preserved under a diffeomorphism. The map K yields the Klein model of hyperbolic geometry. The map extends to a homeomorphism of the unit disk onto itself which is the identity on the unit circle. Thus by continuity the map K extends to the endpoints of geodesics, so carries the arc of the circle in the disc cutting the unit circle orthogonally at two given points on to the straight line segment joining those two points. (Note that on the unit circle the radial derivative of K vanishes, so that the condition on angles no longer applies there.)
2. Convex Polygons
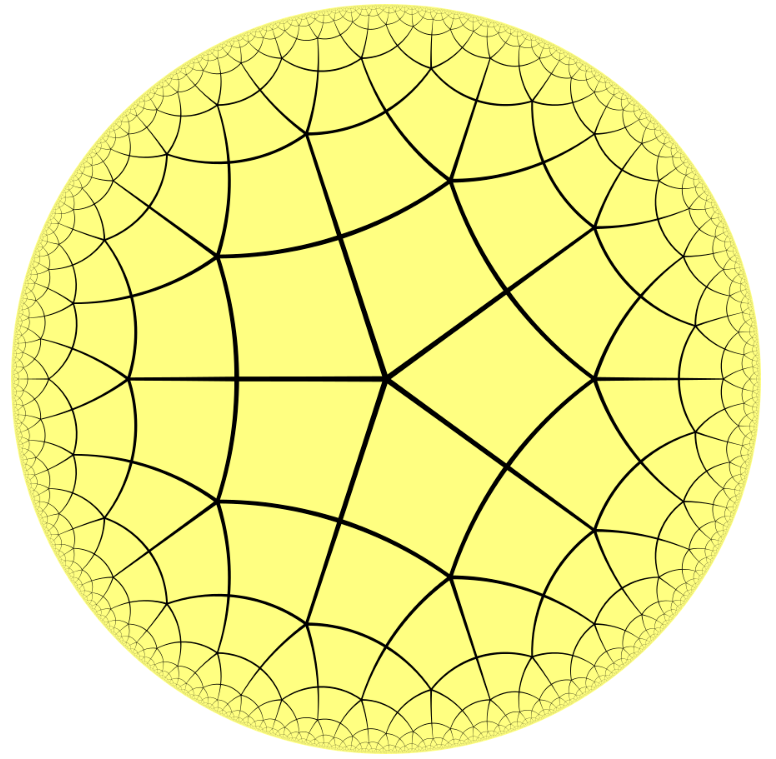
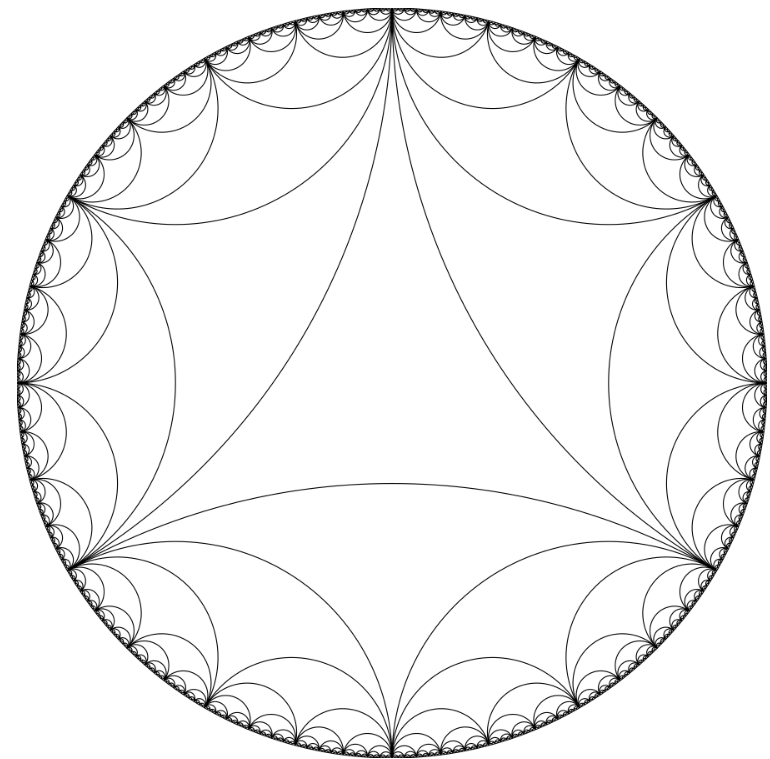
A uniform tiling in the Poincaré disk model by regular convex septagons and triangles.
The same tiling in the Klein model.
In this section the main results on convexity of hyperbolic polygons are deduced from the corresponding results for Euclidean polygons by considering the relation between Poincaré's disk model and the Klein model. A polygon in the unit disk or upper half plane is made up of a collection of a finite set of vertices joined by geodesics, such that none of the geodesics intersect. In the Klein model this corresponds to the same picture in the Euclidean model with straight lines between the vertices. In the Euclidean model the polygon has an interior and exterior (by an elementary version of the Jordan curve theorem), so, since this is preserved under homeomorphism, the same is true in the Poincaré picture.
As a consequence at each vertex there is a well-defined notion of interior angle.
In the Euclidean plane a polygon with all its angles less than π is convex, i.e. the straight line joining interior points of the polygon also lies in the interior of the polygon. Since the Poincaré-Klein map preserves the property that angles are less than π, a hyperbolic polygon with interior angles less than π is carried onto a Euclidean polygon with the same property; the Euclidean polygon is therefore convex and hence, since hyperbolic geodesics are carried onto straight lines, so is the hyperbolic polygon. By a continuity argument, geodesics between points on the sides also lie in the closure of the polygon.
A similar convexity result holds for polygons which have some of their vertices on the boundary of the disk or the upper half plane. In fact each such polygon is an increasing union of polygons with angles less than π. Indeed, take points on the edges at each ideal vertex tending to the two edges joining those points to the ideal point with the geodesic joining them. Since two interior points of the original polygon will lie in the interior of one of these smaller polygons, each of which is convex, the original polygon must also be convex.[4]
3. Tessellation by Schwarz Triangles
In this section tessellations of the hyperbolic upper half plane by Schwarz triangles will be discussed using elementary methods. For triangles without "cusps"—angles equal to zero or equivalently vertices on the real axis—the elementary approach of (Carathéodory 1954) will be followed. For triangles with one or two cusps, elementary arguments of (Evans 1973), simplifying the approach of (Hecke 1935), will be used: in the case of a Schwarz triangle with one angle zero and another a right angle, the orientation-preserving subgroup of the reflection group of the triangle is a Hecke group. For an ideal triangle in which all angles are zero, so that all vertices lie on the real axis, the existence of the tessellation will be established by relating it to the Farey series described in (Hardy Wright) and (Series 2015). In this case the tessellation can be considered as that associated with three touching circles on the Riemann sphere, a limiting case of configurations associated with three disjoint non-nested circles and their reflection groups, the so-called "Schottky groups", described in detail in (Mumford Series). Alternatively—by dividing the ideal triangle into six triangles with angles 0, π/2 and π/3—the tessellation by ideal triangles can be understood in terms of tessellations by triangles with one or two cusps.
3.1. Triangles without Cusps
Tessellation by triangles with angles
π/4,
π/4 and
π/5.
Tessellation by triangles with angles
π/3,
π/5 and
π/7.
Suppose that the hyperbolic triangle Δ has angles π/a, π/b and π/c with a, b, c integers greater than 1. The hyperbolic area of Δ equals π – π/a – π/b – π/c, so that
- [math]\displaystyle{ \frac1a + \frac1b + \frac1c \lt 1. }[/math]
The construction of a tessellation will first be carried out for the case when a, b and c are greater than 2.[5]
The original triangle Δ gives a convex polygon P1 with 3 vertices. At each of the three vertices the triangle can be successively reflected through edges emanating from the vertices to produce 2m copies of the triangle where the angle at the vertex is π/m. The triangles do not overlap except at the edges, half of them have their orientation reversed and they fit together to tile a neighborhood of the point. The union of these new triangles together with the original triangle form a connected shape P2. It is made up of triangles which only intersect in edges or vertices, forms a convex polygon with all angles less than or equal to π and each side being the edge of a reflected triangle. In the case when angle of Δ equals π/3, a vertex of P2 will have an interior angle of π, but this does not affect the convexity of P2. Even in this degenerate case when an angle of π arises, the two collinear edge are still considered as distinct for the purposes of the construction.
The construction of P2 can be understood more clearly by noting that some triangles or tiles are added twice, the three which have a side in common with the original triangle. The rest have only a vertex in common. A more systematic way of performing the tiling is first to add a tile to each side (the reflection of the triangle in that edge) and then fill in the gaps at each vertex. This results in a total of 3 + (2a – 3) + (2b - 3) + (2c - 3) = 2(a + b + c) - 6 new triangles. The new vertices are of two types. Those which are vertices of the triangles attached to sides of the original triangle, which are connected to 2 vertices of Δ. Each of these lie in three new triangles which intersect at that vertex. The remainder are connected to a unique vertex of Δ and belong to two new triangles which have a common edge. Thus there are 3 + (2a – 4) + (2b - 4) + (2c - 4) = 2(a + b + c) - 9 new vertices. By construction there is no overlapping. To see that P2 is convex, it suffices to see that the angle between sides meeting at a new vertex make an angle less than or equal to π. But the new vertices lies in two or three new triangles, which meet at that vertex, so the angle at that vertex is no greater than 2π/3 or π, as required.
This process can be repeated for P2 to get P3 by first adding tiles to each edge of P2 and then filling in the tiles round each vertex of P2. Then the process can be repeated from P3, to get P4 and so on, successively producing Pn from Pn – 1. It can be checked inductively that these are all convex polygons, with non-overlapping tiles. Indeed, as in the first step of the process there are two types of tile in building Pn from Pn – 1, those attached to an edge of Pn – 1 and those attached to a single vertex. Similarly there are two types of vertex, one in which two new tiles meet and those in which three tiles meet. So provided that no tiles overlap, the previous argument shows that angles at vertices are no greater than π and hence that Pn is a convex polygon.[6]
It therefore has to be verified that in constructing Pn from Pn − 1:[7]
(a) the new triangles do not overlap with Pn − 1 except as already described;
(b) the new triangles do not overlap with each other except as already described;
(c) the geodesic from any point in Δ to a vertex of the polygon
Pn – 1 makes an angle ≤ 2
π/3 with each of the edges of the polygon at that vertex.
To prove (a), note that by convexity, the polygon Pn − 1 is the intersection of the convex half-spaces defined by the full circular arcs defining its boundary. Thus at a given vertex of Pn − 1 there are two such circular arcs defining two sectors: one sector contains the interior of Pn − 1, the other contains the interiors of the new triangles added around the given vertex. This can be visualized by using a Möbius transformation to map the upper half plane to the unit disk and the vertex to the origin; the interior of the polygon and each of the new triangles lie in different sectors of the unit disk. Thus (a) is proved.
Before proving (c) and (b), a Möbius transformation can be applied to map the upper half plane to the unit disk and a fixed point in the interior of Δ to the origin.
The proof of (c) proceeds by induction. Note that the radius joining the origin to a vertex of the polygon Pn − 1 makes an angle of less than 2π/3 with each of the edges of the polygon at that vertex if exactly two triangles of Pn − 1 meet at the vertex, since each has an angle less than or equal to π/3 at that vertex. To check this is true when three triangles of Pn − 1 meet at the vertex, C say, suppose that the middle triangle has its base on a side AB of Pn − 2. By induction the radii OA and OB makes angles of less than or equal to 2π/3 with the edge AB. In this case the region in the sector between the radii OA and OB outside the edge AB is convex as the intersection of three convex regions. By induction the angles at A and B are greater than or equal to π/3. Thus the geodesics to C from A and B start off in the region; by convexity, the triangle ABC lies wholly inside the region. The quadrilateral OACB has all its angles less than π (since OAB is a geodesic triangle), so is convex. Hence the radius OC lies inside the angle of the triangle ABC near C. Thus the angles between OC and the two edges of Pn – 1 meeting at C are less than or equal to π/3 + π/3 = 2π/3, as claimed.
To prove (b), it must be checked how new triangles in Pn intersect.
First consider the tiles added to the edges of Pn – 1. Adopting similar notation to (c), let AB be the base of the tile and C the third vertex. Then the radii OA and OB make angles of less than or equal to 2π/3 with the edge AB and the reasoning in the proof of (c) applies to prove that the triangle ABC lies within the sector defined by the radii OA and OB. This is true for each edge of Pn – 1. Since the interiors of sectors defined by distinct edges are disjoint, new triangles of this type only intersect as claimed.
Next consider the additional tiles added for each vertex of Pn – 1. Taking the vertex to be A, three are two edges AB1 and AB2 of Pn – 1 that meet at A. Let C1 and C2 be the extra vertices of the tiles added to these edges. Now the additional tiles added at A lie in the sector defined by radii OB1 and OB2. The polygon with vertices C2 O, C1, and then the vertices of the additional tiles has all its internal angles less than π and hence is convex. It is therefore wholly contained in the sector defined by the radii OC1 and OC2. Since the interiors of these sectors are all disjoint, this implies all the claims about how the added tiles intersect.
Tessellation by triangles with angles
π/2,
π/3 and
π/7.
Tessellation by triangles with angles
π/2,
π/4 and
π/5.
Finally it remains to prove that the tiling formed by the union of the triangles covers the whole of the upper half plane. Any point z covered by the tiling lies in a polygon Pn and hence a polygon Pn +1 . It therefore lies in a copy of the original triangle Δ as well as a copy of P2 entirely contained in Pn +1 . The hyperbolic distance between Δ and the exterior of P2 is equal to r > 0. Thus the hyperbolic distance between z and points not coverered by the tiling is at least r. Since this applies to all points in the tiling, the set covered by the tiling is closed. On the other hand, the tiling is open since it coincides with the union of the interiors of the polygons Pn. By connectivity, the tessellation must cover the whole of the upper half plane.
To see how to handle the case when an angle of Δ is a right angle, note that the inequality
- [math]\displaystyle{ \frac1a + \frac1b + \frac1c \lt 1 }[/math].
implies that if one of the angles is a right angle, say a = 2, then both b and c are greater than 2 and one of them, b say, must be greater than 3. In this case, reflecting the triangle across the side AB gives an isosceles hyperbolic triangle with angles π/c, π/c and 2π/b. If 2π/b ≤ π/3, i.e. b is greater than 5, then all the angles of the doubled triangle are less than or equal to π/3. In that case the construction of the tessellation above through increasing convex polygons adapts word for word to this case except that around the vertex with angle 2π/b, only b—and not 2b—copies of the triangle are required to tile a neighborhood of the vertex. This is possible because the doubled triangle is isosceles. The tessellation for the doubled triangle yields that for the original triangle on cutting all the larger triangles in half.[8]
It remains to treat the case when b equals 4 or 5. If b = 4, then c ≥ 5: in this case if c ≥ 6, then b and c can be switched and the argument above applies, leaving the case b = 4 and c = 5. If b = 5, then c ≥ 4. The case c ≥ 6 can be handled by swapping b and c, so that the only extra case is b = 5 and c = 5. This last isosceles triangle is the doubled version of the first exceptional triangle, so only that triangle Δ1—with angles π/2, π/4 and π/5 and hyperbolic area π/20—needs to be considered (see below). (Carathéodory 1954) handles this case by a general method which works for all right angled triangles for which the two other angles are less than or equal to π/4. The previous method for constructing P2, P3, ... is modified by adding an extra triangle each time an angle 3π/2 arises at a vertex. The same reasoning applies to prove there is no overlapping and that the tiling covers the hyperbolic upper half plane.[8]
On the other hand, the given configuration gives rise to an arithmetic triangle group. These were first studied in (Fricke Klein). and have given rise to an extensive literature. In 1977 Takeuchi obtained a complete classification of arithmetic triangle groups (there are only finitely many) and determined when two of them are commensurable. The particular example is related to Bring's curve and the arithmetic theory implies that the triangle group for Δ1 contains the triangle group for the triangle Δ2 with angles π/4, π/4 and π/5 as a non-normal subgroup of index 6.[9]
Doubling the triangles Δ1 and Δ2, this implies that there should be a relation between 6 triangles Δ3 with angles π/2, π/5 and π/5 and hyperbolic area π/10 and a triangle Δ4 with angles π/5, π/5 and π/10 and hyperbolic area 3π/5. (Threlfall 1932) established such a relation directly by completely elementary geometric means, without reference to the arithmetic theory: indeed as illustrated in the fifth figure below, the quadrilateral obtained by reflecting across a side of a triangle of type Δ4 can be tiled by 12 triangles of type Δ3. The tessellation by triangles of the type Δ4 can be handled by the main method in this section; this therefore proves the existence of the tessellation by triangles of type Δ3 and Δ1.[10]
Tessellation by triangles with angles π/2, π/5 and π/5.
Tessellation obtained by coalescing two triangles.
Tiling with pentagons formed from 10 (2,5,5) triangles.
Adjusting to tiling by triangles with angles π/5, π/10, π/10.
Tiling 2 (5,10,10) triangles with 12 (2,5,5) triangles.
3.2. Triangles with One or Two Cusps
In the case of a Schwarz triangle with one or two cusps, the process of tiling becomes simpler; but it is easier to use a different method going back to Hecke to prove that these exhaust the hyperbolic upper half plane.
In the case of one cusp and non-zero angles π/a, π/b with a, b integers greater than one, the tiling can be envisaged in the unit disk with the vertex having angle π/a at the origin. The tiling starts by adding 2a – 1 copies of the triangle at the origin by successive reflections. This results in a polygon P1 with 2a cusps and between each two 2a vertices each with an angle π/b. The polygon is therefore convex. For each non-ideal vertex of P1, the unique triangle with that vertex can be similar reflected around that vertex, thus adding 2b – 1 new triangles, 2b – 1 new ideal points and 2 b – 1 new vertices with angle π/a. The resulting polygon P2 is thus made up of 2a(2b – 1) cusps and the same number of vertices each with an angle of π/a, so is convex. The process can be continued in this way to obtain convex polygons P3, P4, and so on. The polygon Pn will have vertices having angles alternating between 0 and π/a for n even and between 0 and π/b for n odd. By construction the triangles only overlap at edges or vertices, so form a tiling.[11]
Tessellation by triangle with angles 0, π/3, π/5.
Tessellation by triangle with angles 0, π/5, π/2.
Tessellation by triangle with angles 0, 0, π/5.
The case where the triangle has two cusps and one non-zero angle π/a can be reduced to the case of one cusp by observing that the trinale is the double of a triangle with one cusp and non-zero angles π/a and π/b with b = 2. The tiling then proceeds as before.[12]
To prove that these give tessellations, it is more convenient to work in the upper half plane. Both cases can be treated simultaneously, since the case of two cusps is obtained by doubling a triangle with one cusp and non-zero angles π/a and π/2. So consider the geodesic triangle in the upper half plane with angles 0, π/a, π/b with a, b integers greater than one. The interior of such a triangle can be realised as the region X in the upper half plane lying outside the unit disk |z| ≤ 1 and between two lines parallel to the imaginary axis through points u and v on the unit circle. Let Γ be the triangle group generated by the three reflections in the sides of the triangle.
To prove that the successive reflections of the triangle cover the upper half plane, it suffices to show that for any z in the upper half plane there is a g in Γ such that g(z) lies in X. This follows by an argument of (Evans 1973), simplified from the theory of Hecke groups. Let λ = Re a and μ = Re b so that, without loss of generality, λ < 0 ≤ μ. The three reflections in the sides are given by.
Thus T = R3∘R2 is translation by μ − λ. It follows that for any z1 in the upper half plane, there is an element g1 in the subgroup Γ1 of Γ generated by T such that w1 = g1(z1) satisfies λ ≤ Re w1 ≤ μ, i.e. this strip is a fundamental domain for the translation group Γ1. If |w1| ≥ 1, then w1 lies in X and the result is proved. Otherwise let z2 = R1(w1) and find g2 Γ1 such that w2 = g2(z2) satisfies λ ≤ Re w2 ≤ μ. If |w2| ≥ 1 then the result is proved. Continuing in this way, either some wn satisfies |wn| ≥ 1, in which case the result is proved; or |wn| < 1 for all n. Now since gn + 1 lies in Γ1 and |wn| < 1,
- [math]\displaystyle{ \operatorname{Im} g_{n+1}(z_{n+1}) = \operatorname{Im} z_{n+1} = \operatorname{Im} \frac{w_n}{|w_n|{}^2} = \frac{\operatorname{Im} w_n}{|w_n|{}^2}. }[/math]
In particular
- [math]\displaystyle{ \operatorname{Im} w_{n+1} \ge \operatorname{Im} w_n }[/math]
and
- [math]\displaystyle{ \frac{\operatorname{Im} w_{n+1}}{\operatorname{Im} w_n} = |w_n|^{-2} \ge 1. }[/math]
Thus, from the inequality above, the points (wn) lies in the compact set |z| ≤ 1, λ ≤ Re z ≤ μ and Im z ≥ Im w 1. It follows that |wn| tends to 1; for if not, then there would be an r < 1 such that |wm| ≤ r for inifitely many m and then the last equation above would imply that Im wn tends to infinity, a contradiction.
Let w be a limit point of the wn, so that |w| = 1. Thus w lies on the arc of the unit circle between u and v. If w ≠ u, v, then R1 wn would lie in X for n sufficiently large, contrary to assumption. Hence w =u or v. Hence for n sufficiently large wn lies close to u or v and therefore must lie in one of the reflections of the triangle about the vertex u or v, since these fill out neighborhoods of u and v. Thus there is an element g in Γ such that g(wn) lies in X. Since by construction wn is in the Γ-orbit of z1, it follows that there is a point in this orbit lying in X, as required.[13]
3.3. Ideal Triangles
The tessellation for an ideal triangle with all its vertices on the unit circle and all its angles 0 can be considered as a special case of the tessellation for a triangle with one cusp and two now zero angles π/3 and π/2. Indeed, the ideal triange is made of six copies one-cusped triangle obtained by reflecting the smaller triangle about the vertex with angle π/3.
Tessellation for triangle with angles 0, π/3 and π/2.
Tessellation for ideal triangle.
Second realisation of tessellation for ideal triangle.
Line drawing of tessellation by ideal triangles.
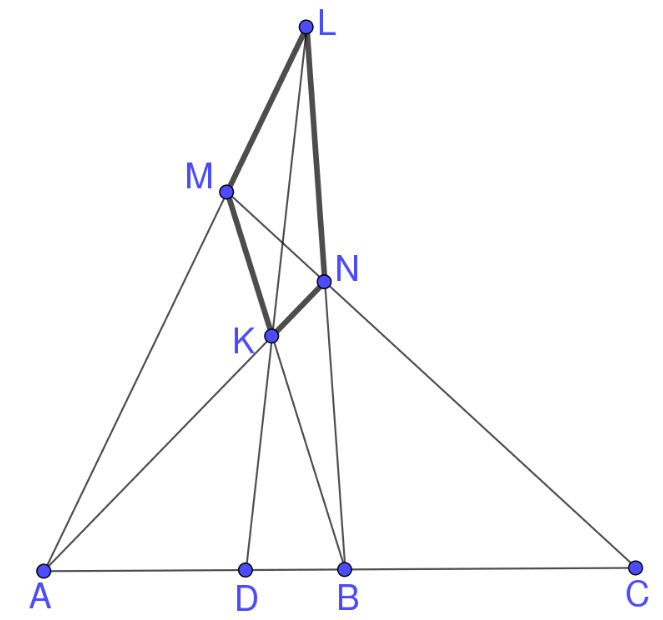
D is the harmonic conjugate of
C with respect to
A and
B.
Reflection of an ideal triangle in one of its sides.
Each step of the tiling, however, is uniquely determined by the positions of the new cusps on the circle, or equivalently the real axis; and these points can be understood directly in terms of Farey series following (Series 2015), (Hatcher 2013) and (Hardy Wright). This starts from the basic step that generates the tessellation, the reflection of an ideal triangle in one of its sides. Reflection corresponds to the process of inversion in projective geometry and taking the projective harmonic conjugate, which can be defined in terms of the cross ratio. In fact if p, q, r, s are distinct points in the Riemann sphere, then there is a unique complex Möbius transformation g sending p, q and s to 0, ∞ and 1 respectively. The cross ratio (p, q; r, s) is defined to be g(r) and is given by the formula
- [math]\displaystyle{ (p, q; r, s) = \frac{(p-r)(q-s)}{(p-s)(q-r)}. }[/math]
By definition it is invariant under Möbius transformations. If a, b lie on the real axis, the harmonic conjugate of c with respect to a and b is defined to be the unique real number d such that (a, b; c, d) = −1. So for example if a = 1 and b = –1, the conjugate of r is 1/r. In general Möbius invariance can be used to obtain an explicit formula for d in terms of a, b and c. Indeed, translating the centre t = (a + b)/2 of the circle with diameter having endpoints a and b to 0, d – t is the harmonic conjugate of c – t with respect to a - t and b – t. The radius of the circle is ρ = (b – a)/2 so (d - t)/ρ is the harmonic conjugate of (c – t)/ρ with respect to 1 and -1. Thus
- [math]\displaystyle{ \frac{d-t}\rho = \frac\rho{c-t} }[/math]
so that
- [math]\displaystyle{ d = \frac{\rho^2}{r-t} + t = \frac{(c-a)b + (c-b)a}{(c-a) + (c-b)}. }[/math]
It will now be shown that there is a parametrisation of such ideal triangles given by rationals in reduced form
- [math]\displaystyle{ a = \frac{p_1}{q_1},\ b = \frac{p_1 + p_2}{q_1 + q_2},\ c = \frac{p_2}{q_2} }[/math]
with a and c satisfying the "neighbour condition" p2q1 − q2p1 = 1.
The middle term b is called the Farey sum or mediant of the outer terms and written
- [math]\displaystyle{ b = a \oplus c. }[/math]
The formula for the reflected triangle gives
- [math]\displaystyle{ d = \frac{p_1 + 2p_2}{q_1 + 2q_2} = a \oplus b. }[/math]
Similarly the reflected triangle in the second semicircle gives a new vertex b ⊕ c. It is immediately verified that a and b satisfy the neighbour condition, as do b and c.
Now this procedure can be used to keep track of the triangles obtained by successively reflecting the basic triangle Δ with vertices 0, 1 and ∞. It suffices to consider the strip with 0 ≤ Re z ≤ 1, since the same picture is reproduced in parallel strips by applying reflections in the lines Re z = 0 and 1. The ideal triangle with vertices 0, 1, ∞ reflects in the semicircle with base [0,1] into the triangle with vertices a = 0, b = 1/2, c = 1. Thus a = 0/1 and c = 1/1 are neighbours and b = a ⊕ c. The semicircle is split up into two smaller semicircles with bases [a,b] and [b,c]. Each of these intervals splits up into two intervals by the same process, resulting in 4 intervals. Continuing in this way, results into subdivisions into 8, 16, 32 intervals, and so on. At the nth stage, there are 2n adjacent intervals with 2n + 1 endpoints. The construction above shows that successive endpoints satisfy the neighbour condition so that new endpoints resulting from reflection are given by the Farey sum formula.
To prove that the tiling covers the whole hyperbolic plane, it suffices to show that every rational in [0,1] eventually occurs as an endpoint. There are several ways to see this. One of the most elementary methods is described in (Graham Knuth) in their development—without the use of continued fractions—of the theory of the Stern-Brocot tree, which codifies the new rational endpoints that appear at the nth stage. They give a direct proof that every rational appears. Indeed, starting with {0/1,1/1}, successive endpoints are introduced at level n+1 by adding Farey sums or mediants (p+r)/(q+s) between all consecutive terms p/q, r/s at the nth level (as described above). Let x = a/b be a rational lying between 0 and 1 with a and b coprime. Suppose that at some level x is sandwiched between successive terms p/q < x < r/s. These inequalities force aq – bp ≥ 1 and br – as ≥ 1 and hence, since rp – qs = 1,
- [math]\displaystyle{ a + b = (r+s)(ap-bq) + (p+q)(br -as) \ge p+q+r+s. }[/math]
This puts an upper bound on the sum of the numerators and denominators. On the other hand, the mediant (p+r)/(q+s) can be introduced and either equals x, in which case the rational x appears at this level; or the mediant provides a new interval containing x with strictly larger numerator-and-denominator sum. The process must therefore terminate after at most a + b steps, thus proving that x appears.[14]
A second approach relies on the modular group G = SL(2,Z).[15] The Euclidean algorithm implies that this group is generated by the matrices
- [math]\displaystyle{ S=\begin{pmatrix} 0 & 1\\ -1 & 0 \end{pmatrix},\,\,\, T=\begin{pmatrix} 1 & 1\\ 0 & 1 \end{pmatrix}. }[/math]
In fact let H be the subgroup of G generated by S and T. Let
- [math]\displaystyle{ g=\begin{pmatrix} a & b\\ c & d\end {pmatrix} }[/math]
be an element of SL(2,Z). Thus ad − cb = 1, so that a and c are coprime. Let
- [math]\displaystyle{ v=\begin{pmatrix}a\\ c\end{pmatrix},\,\,\, u= \begin{pmatrix}1\\ 0\end{pmatrix}. }[/math]
Applying S if necessary, it can be assumed that |a| > |c| (equality is not possible by coprimeness). We write a = mc + r with 0 ≤ r ≤ |c|. But then
- [math]\displaystyle{ T^{-m}\begin{pmatrix} a\\ c \end{pmatrix} = \begin{pmatrix} r\\ c\end{pmatrix}. }[/math]
This process can be continued until one of the entries is 0, in which case the other is necessarily ±1. Applying a power of S if necessary, it follows that v = h u for some h in H. Hence
- [math]\displaystyle{ h^{-1}g=\begin{pmatrix}1 & p\\ 0 & q\end{pmatrix} }[/math]
with p, q integers. Clearly p = 1, so that h−1g = Tq. Thus g = h Tq lies in H as required.
To prove that all rationals in [0,1] occur, it suffices to show that G carries Δ onto triangles in the tessellation. This follows by first noting that S and T carry Δ on to such a triangle: indeed as Möbius transformations, S(z) = –1/z and T(z) = z + 1, so these give reflections of Δ in two of its sides. But then S and T conjugate the reflections in the sides of Δ into reflections in the sides of SΔ and TΔ, which lie in Γ. Thus G normalizes Γ. Since triangles in the tessellation are exactly those of the form gΔ with g in Γ, it follows that S and T, and hence all elements of G, permute triangles in the tessellation. Since every rational is of the form g(0) for g in G, every rational in [0,1] is the vertex of a triangle in the tessellation.
The reflection group and tessellation for an ideal triangle can also be regarded as a limiting case of the Schottky group for three disjoint unnested circles on the Riemann sphere. Again this group is generated by hyperbolic reflections in the three circles. In both cases the three circles have a common circle which cuts them orthogonally. Using a Möbius transformation, it may be assumed to be the unit circle or equivalently the real axis in the upper half plane.[16]
3.4. Approach of Siegel
In this subsection the approach of Carl Ludwig Siegel to the tessellation theorem for triangles is outlined. Siegel's less elementary approach does not use convexity, instead relying on the theory of Riemann surfaces, covering spaces and a version of the monodromy theorem for coverings. It has been generalized to give proofs of the more general Poincaré polygon theorem. (Note that the special case of tiling by regular n-gons with interior angles 2π/n is an immediate consequence of the tessellation by Schwarz triangles with angles π/n, π/n and π/2.)[17][18]
Let Γ be the free product Z2 ∗ Z2 ∗ Z2. If Δ = ABC is a Schwarz triangle with angles π/a, π/b and π/c, where a, b, c ≥ 2, then there is a natural map of Γ onto the group generated by reflections in the sides of Δ. Elements of Γ are described by a product of the three generators where no two adjacent generators are equal. At the vertices A, B and C the product of reflections in the sides meeting at the vertex define rotations by angles 2π/a, 2π/b and 2π/c; Let gA, gB and gC be the corresponding products of generators of Γ = Z2 ∗ Z2 ∗ Z2. Let Γ0 be the normal subgroup of index 2 of Γ, consisting of elements that are the product of an even number of generators; and let Γ1 be the normal subgroup of Γ generated by (gA)a, (gB)b and (gC)c. These act trivially on Δ. Let Γ = Γ/Γ1 and Γ0 = Γ0/Γ1.
The disjoint union of copies of Δ indexed by elements of Γ with edge identifications has the natural structure of a Riemann surface Σ. At an interior point of a triangle there is an obvious chart. As a point of the interior of an edge the chart is obtained by reflecting the triangle across the edge. At a vertex of a triangle with interior angle π/n, the chart is obtained from the 2n copies of the triangle obtained by reflecting it successively around that vertex. The group Γ acts by deck transformations of Σ, with elements in Γ0 acting as holomorphic mappings and elements not in Γ0 acting as antiholomorphic mappings.
There is a natural map P of Σ into the hyperbolic plane. The interior of the triangle with label g in Γ is taken onto g(Δ), edges are taken to edges and vertices to vertices. It is also easy to verify that a neighbourhood of an interior point of an edge is taken into a neighbourhood of the image; and similarly for vertices. Thus P is locally a homeomorphism and so takes open sets to open sets. The image P(Σ), i.e. the union of the translates g(Δ), is therefore an open subset of the upper half plane. On the other hand, this set is also closed. Indeed, if a point is sufficiently close to Δ it must be in a translate of Δ. Indeed, a neighbourhood of each vertex is filled out the reflections of Δ and if a point lies outside these three neighbourhoods but is still close to Δ it must lie on the three reflections of Δ in its sides. Thus there is δ > 0 such that if z lies within a distance less than δ from Δ, then z lies in a Γ-translate of Δ. Since the hyperbolic distance is Γ-invariant, it follows that if z lies within a distance less than δ from Γ(Δ) it actually lies in Γ(Δ), so this union is closed. By connectivity it follows that P(Σ) is the whole upper half plane.
On the other hand, P is a local homeomorphism, so a covering map. Since the upper half plane is simply connected, it follows that P is one-one and hence the translates of Δ tessellate the upper half plane. This is a consequence of the following version of the monodromy theorem for coverings of Riemann surfaces: if Q is a covering map between Riemann surfaces Σ1 and Σ2, then any path in Σ2 can be lifted to a path in Σ1 and any two homotopic paths with the same end points lift to homotopic paths with the same end points; an immediate corollary is that if Σ2 is simply connected, Q must be a homeomorphism.[19] To apply this, let Σ1 = Σ, let Σ2 be the upper half plane and let Q = P. By the corollary of the monodromy theorem, P must be one-one.
It also follows that g(Δ) = Δ if and only if g lies in Γ1, so that the homomorphism of Γ0 into the Möbius group is faithful.
4. Conformal Mapping of Schwarz Triangles
In this section Schwarz's explicit conformal mapping from the unit disc or the upper half plane to the interior of a Schwarz triangle will be constructed as the ratio of solutions of a hypergeometric ordinary differential equation, following (Carathéodory 1954), (Nehari 1975) and (Hille 1976).
5. Applications
The Schwarz triangle functions for spherical Schwarz triangles are relevant to conformal map projections. The inverse of such functions are rational functions that map Schwarz triangles alternatingly to the upper half-plane and lower half-plane. These can be constructed with the numerator polynomial having zeros for vertices mapped to zero, the denominator polynomial having zeros for vertices mapped to infinity, and a leading constant term determining which vertices are mapped to 1. The planar case is also relevant: the Schwarz triangle in this case can be expressed using Jacobi elliptic functions for right triangles and Dixon elliptic functions for equilateral triangles.[20]