1. Method

X-ray solution scattering curves computed from atomic models of twenty-five different proteins with molecular masses between 10 and 300 kDa. CC BY-SA 3.0, https://en.wikipedia.org/w/index.php?curid=13264733

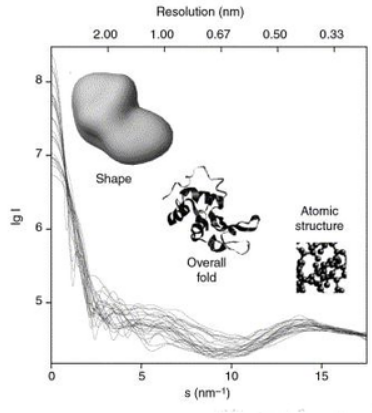
Conceptually, small-angle scattering experiments are simple: the sample is exposed to X-rays or neutrons and the scattered radiation is registered by a detector. As the SAS measurements are performed very close to the primary beam ("small angles"), the technique needs a highly collimated or focused X-ray or neutron beam. The biological small-angle X-ray scattering is often performed at synchrotron radiation sources, because biological molecules normally scatter weakly and the measured solutions are dilute. The biological SAXS method profits from the high intensity of X-ray photon beams provided by the synchrotron storage rings. The X-ray or neutron scattering curve (intensity versus scattering angle) is used to create a low-resolution model of a protein, shown here on the right picture. One can further use the X-ray or neutron scattering data and fit separate domains (X-ray or NMR structures) into the "SAXS envelope".

In a scattering experiment, a solution of macromolecules is exposed to X-rays (with wavelength λ typically around 0.15 nm) or thermal neutrons (λ≈0.5 nm). The scattered intensity I(s) is recorded as a function of momentum transfer s (s=4πsinθ/λ, where 2θ is the angle between the incident and scattered radiation). From the intensity of the solution the scattering from only the solvent is subtracted. The random positions and orientations of particles result in an isotropic intensity distribution which, for monodisperse non-interacting particles, is proportional to the scattering from a single particle averaged over all orientations. The net particle scattering is proportional to the squared difference in scattering length density (electron density for X-rays and nuclear/spin density for neutrons) between particle and solvent – the so-called contrast. The contrast can be varied in neutron scattering using H₂O/D₂O mixtures or selective deuteration to yield additional information.^[1] The information content of SAS data is illustrated here in the figure on the right, which shows X-ray scattering patterns from proteins with different folds and molecular masses. At low angles (2-3 nm resolution) the curves are rapidly decaying functions of s essentially determined by the particle shape, which clearly differ. At medium resolution (2 to 0.5 nm) the differences are already less pronounced and above 0.5 nm resolution all curves are very similar.^[2] SAS thus contains information about the gross structural features – shape, quaternary and tertiary structure – but is not suitable for the analysis of the atomic structure.

2. History

First applications date back to the late 1930s when the main principles of SAXS were developed in the fundamental work of Guinier following his studies of metallic alloys. In the first monograph on SAXS by Guinier and Fournet it was already demonstrated that the method yields not only information on the sizes and shapes of particles but also on the internal structure of disordered and partially ordered systems.

In the 1960s, the method became increasingly important in the study of biological macromolecules in solution as it allowed one to get low-resolution structural information on the overall shape and internal structure in the absence of crystals. A breakthrough in SAXS and SANS experiments came in the 1970s, thanks to the availability of synchrotron radiation and neutron sources, the latter paving the way for contrast variation by solvent exchange of H₂O for D₂O and specific deuteration methods. It was realised that scattering studies on solution provide, at a minimal investment of time and effort, useful insights into the structure of non-crystalline biochemical systems. Moreover, SAXS/SANS also made possible real time investigations of intermolecular interactions, including assembly and large-scale conformational changes in macromolecular assemblies.

The main challenge of SAS as a structural method is to extract information about the three-dimensional structure of the object from the one-dimensional experimental data. In the past, only overall particle parameters (e.g. volume, radius of gyration) of the macromolecules were directly determined from the experimental data, whereas the analysis in terms of three-dimensional models was limited to simple geometrical bodies (e.g. ellipsoids, cylinders, etc.) or was performed on an ad hoc trial-and-error basis. Electron microscopy was often used as a constraint in building consensus models. In the 1980s, progress in other structural methods led to a decline of the interest of biochemists in SAS studies, which drew structural conclusions from just a couple of overall parameters or were based on trial-and-error models.

The 1990s brought a breakthrough in SAXS/SANS data analysis methods, which opened the way for reliable ab initio modelling of macromolecular complexes, including detailed determination of shape and domain structure and application of rigid body refinement techniques. This progress was accompanied by further advances in instrumentation, allowing sub-ms time resolutions to be achieved on third generation SR sources in the studies of protein and nucleic acid folding.^[1]

In 2005, a four-year project was started. Small-Angle X-Ray scattering Initiative for EuRope (SAXIER) with the goal to combine SAXS methods with other analytical techniques and create automated software to rapidly analyse large quantities of data. The project created a unified European SAXS infrastructure, using the most advanced methods available.^[3]

3. Data Analysis

In a good quality SAS experiment, several solutions with varying concentrations of the macromolecule under investigation are measured. By extrapolating the scattering curves measured at different concentrations to zero concentration, one is able to obtain a scattering curve that represents infinite dilution. Then concentration effects should not affect the scattering curve. Data analysis of the extrapolated scattering curve begins with the inspection of the start of the scattering curve in the region around s = 0. If the region follows the Guinier approximation (also known as Guinier law), the sample is not aggregated. Then the shape of the particle in question can be determined by various methods, of which some are described in the following reference.^[1]

3.1. Indirect Fourier Transform

First step is usually to compute a Fourier transform of the scattering curve. Transformed curve can be interpreted as distance distribution function inside a particle. This transformation gives also a benefit of regularization of input data.

3.2. Low-resolution Models

Lysozyme models built by different methods. Left - overall shape reconstructed by SASHA; middle - dummy residue model, built by DAMMIN; DAMMIF; right - chain compatible GASBOR model. CC BY-SA 3.0, https://en.wikipedia.org/w/index.php?curid=13323600

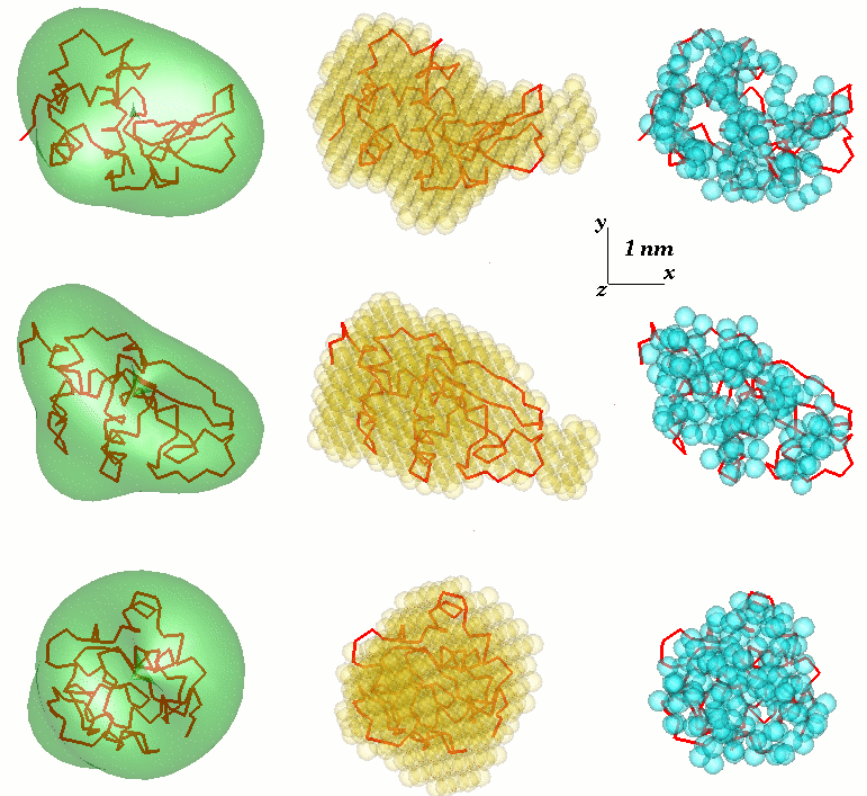
One problem in SAS data analysis is to get a three-dimensional structure from a one-dimensional scattering pattern. The SAS data does not imply a single solution. Many different proteins, for example, may have the same scattering curve. Reconstruction of 3D structure might result in large number of different models. To avoid this problem a number of simplifications need to be considered.

An additional approach is to combine small-angle X-ray and neutron scattering data and model with the program MONSA.

Freely available SAS analysis computer programs have been intensively developed at EMBL. In the first general ab initio approach, an angular envelope function of the particle r=F(ω), where (r,ω) are spherical coordinates, is described by a series of spherical harmonics. The low resolution shape is thus defined by a few parameters – the coefficients of this series – which fit the scattering data. The approach was further developed and implemented in the computer program SASHA (Small Angle Scattering Shape Determination).^[4][5] It was demonstrated that under certain circumstances a unique envelope can be extracted from the scattering data. This method is only applicable to globular particles with relatively simple shapes and without significant internal cavities. To overcome these limitations, there was another approach developed, which uses different types of Monte-Carlo searches. DALAI_GA is an elegant program, which takes a sphere with diameter equal to the maximum particle size Dmax, which is determined from the scattering data, and fills it with beads. Each bead belongs either to the particle (index=1) or to the solvent (index=0). The shape is thus described by the binary string of length M. Starting from a random string, a genetic algorithm searches for a model that fits the data. Compactness and connectivity constrains are imposed in the search, implemented in the program DAMMIN.^[6][7] If the particle symmetry is known, SASHA and DAMMIN can utilise it as useful constraints. The 'give-n-take' procedure SAXS3D and the program SASMODEL, based on interconnected ellipsoids are ab initio Monte Carlo approaches without limitation in the search space.^[2]

An approach that uses an ensemble of Dummy Residues (DRs) and simulated annealing to build a locally "chain-compatible" DR-model inside a sphere of diameter Dmax lets one extract more details from SAXS data. This method is implemented in the program GASBOR.^[8][9]

Solution scattering patterns of multi-domain proteins and macromolecular complexes can also be fitted using models built from high resolution (NMR or X-ray) structures of individual domains or subunits assuming that their tertiary structure is preserved. Depending on the complexity of the object, different approaches are employed for the global search of the optimum configuration of subunits fitting the experimental data.

3.3. Consensus Model

The Monte-Carlo based models contain hundreds or thousand parameters, and caution is required to avoid overinterpretation. A common approach is to align a set of models resulting from independent shape reconstruction runs to obtain an average model retaining the most persistent- and conceivably also most reliable-features (e.g. using the program SUPCOMB).^[2][10][11]

3.4. Adding Missing Loops

Disordered surface amino acids ("loops") are frequently unobserved in NMR and crystallographic studies, and may be left missing in the reported models. Such disordered element contribute to the scattering intensity and their probable locations can be found by fixing the known part of the structure and adding the missing parts to fit the SAS pattern from the entire particle. The Dummy Residue approach was extended and the algorithms for adding missing loops or domains were implemented in the program suite CREDO.^[2]

3.5. Hybrid Methods

Recently a few methods proposed that use SAXS data as constraints. The authors aimed to improve results of fold recognition^[12] and de novo protein structure prediction^[13] methods. SAXS data provide the Fourier transform of the histogram of atomic pair distances (pair distribution function) for a given protein. This can serve as a structural constraint on methods used to determine the native conformational fold of the protein. Threading or fold recognition assumes that 3D structure is more conserved than sequence. Thus, very divergent sequences may have similar structure. Ab initio methods, on the other hand, challenge one of the biggest problems in molecular biology, namely, to predict the folding of a protein "from scratch", using no homologous sequences or structures. Using the "SAXS filter", the authors were able to purify the set of de novo protein models significantly.^[13] This was further proved by structure homology searches. It was also shown, that the combination of SAXS scores with scores, used in threading methods, significantly improves the performance of fold recognition.^[12] On one example it was demonstrated how approximate tertiary structure of modular proteins can be assembled from high resolution NMR structures of domains, using SAXS data, confining the translational degrees of freedom.^[14] Another example shows how the SAXS data can be combined together with NMR, X-ray crystallography and electron microscopy to reconstruct the quaternary structure of multidomain protein.^[15]

3.6. Flexible Systems

An elegant method to tackle the problem of intrinsically disordered or multi-domain proteins with flexible linkers was proposed recently.^[16] It allows coexistence of different conformations of a protein, which together contribute to the average experimental scattering pattern. Initially, EOM (ensemble optimization method) generates a pool of models covering the protein configuration space. The scattering curve is then calculated for each model. In the second step, the program selects subsets of protein models. Average experimental scattering is calculated for each subset and fitted to the experimental SAXS data. If the best fit is not found, models are reshuffled between different subsets and new average scattering calculation and fitting to the experimental data is performed. This method has been tested on two proteins– denatured lysozyme and Bruton's protein kinase. It gave some interesting and promising results.^[16]

4. Biological Molecule Layers and GISAS

Coatings of biomolecules can be studied with grazing-incidence X-ray and neutron scattering. IsGISAXS (grazing incidence small angle X-ray scattering) is a software program dedicated to the simulation and analysis of GISAXS from nanostructures. IsGISAXS only encompasses the scattering by nanometric sized particles, which are buried in a matrix subsurface or supported on a substrate or buried in a thin layer on a substrate. The case of holes is also handled. The geometry is restricted to a plane of particles. The scattering cross section is decomposed in terms of interference function and particle form factor. The emphasis is put on the grazing incidence geometry which induces a "beam refraction effect". The particle form factor is calculated within the distorted wave Born approximation (DWBA), starting as an unperturbed state with sharp interfaces or with the actual perpendicular profile of refraction index. Various kinds of simple geometrical shapes are available with a full account of size and shape distributions in the Decoupling Approximation (DA), in the local monodisperse approximation (LMA) and also in the size-spacing correlation approximation (SSCA). Both, disordered systems of particles defined by their particle-particle pair correlation function and bi-dimensional crystal or para-crystal are considered.^[17]