
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Sirius Huang | -- | 1759 | 2022-09-27 02:52:27 | | | |
| 2 | Sirius Huang | + 90 word(s) | 1849 | 2022-09-27 11:34:59 | | |
Video Upload Options
Six-rays model is applied in an urban or indoor environment where a radio signal transmitted will encounter some objects that produce reflected, refracted or scattered copies of the transmitted signal. These are called multipath signal components, they are attenuated, delayed and shifted from the original signal (LOS) due to a finite number of reflectors with known location and dielectric properties, LOS and multipath signal are summed at the receiver. This model approach the propagation of electromagnetic waves by representing wavefront as simple particles. Thus reflection, refraction and scattering effects are approximated using simple geometric equation instead Maxwell's wave equations. The simplest model is two-rays which predicts signal variation resulting from a ground reflection interfering with the loss path. This model is applicable in isolated areas with some reflectors, such as rural roads or hallway. The above two-rays approach can easily be extended to add as many rays as required. We may add rays bouncing off each side of a street in an urban corridor, leading to a six-rays model. The deduction of the six-rays model is presented below.
1. Mathematical Deduction
1.1. Antennas of Heights Equal Located in the Center of the Street
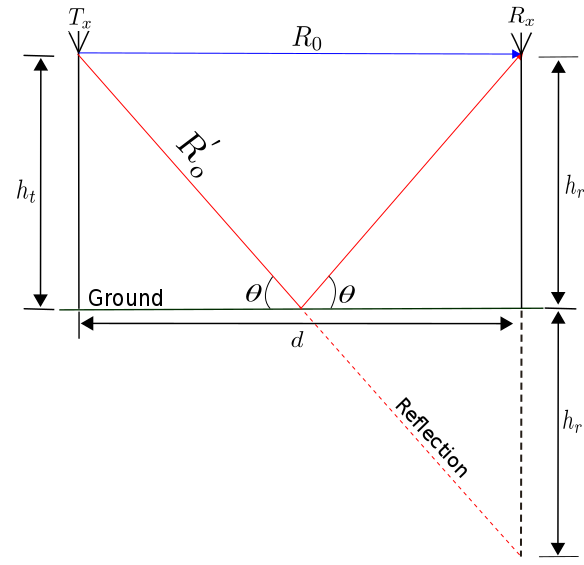

For the analysis of antennas with equal heights then [math]\displaystyle{ h_{t}= h_{r}=h }[/math], determining that for the following two rays that are reflected once in the wall, the point in which they collide is equal to said height [math]\displaystyle{ h }[/math]. Also for each ray that is reflected in the wall, there is another ray that is reflected in the ground in a number equal to the reflections in the wall plus one, in these rays there are diagonal distances for each reflection and the sum of these distances is denominated [math]\displaystyle{ d' }[/math].
Being located in the center of the street the distance between the antennas [math]\displaystyle{ T_{X} }[/math] and [math]\displaystyle{ R_{X} }[/math], the buildings and the width of the streets are equal in both sides so that [math]\displaystyle{ w_{t1}=w_{r1}=w_{t2}=w_{r2} }[/math], defining thus a single distance [math]\displaystyle{ w }[/math].
The mathematical model of propagation of six rays is based on the model of two rays, to find the equations of each ray involved. The distance [math]\displaystyle{ d }[/math] that separates the two antennas, is equal to the first direct ray [math]\displaystyle{ R_{0} }[/math] or line of sight (LOS), that is:
[math]\displaystyle{ R_{0}=d }[/math]
For the ray reflected under [math]\displaystyle{ R_{0} }[/math] applies the theorem of Pythagoras, in the right triangle that forms between the reflection of [math]\displaystyle{ R_{0} }[/math] as the hypotenuse and the direct ray obtaining:
[math]\displaystyle{ R_{0}^{'}=\sqrt{d^{2}+(2*h)^{2}} }[/math]
For [math]\displaystyle{ R_{1} }[/math] the Pythagorean theorem is reapplied, knowing that one of the hinges is double the distances between the transmitter and the building due to the reflection of [math]\displaystyle{ w }[/math] and the diagonal distance to the wall:

[math]\displaystyle{ R_{1}=\sqrt{d^{2}+(2*w)^{2}} }[/math]
For [math]\displaystyle{ R_{1} }[/math] the second ray is multiplied twice but it is taken into account that the distance is half of the third ray to form the equivalent triangle considering that [math]\displaystyle{ d_{1} }[/math] is the half of the distance of [math]\displaystyle{ R_{1} }[/math] and these must be the half of the line of sight distance [math]\displaystyle{ d }[/math]:
[math]\displaystyle{ R_{1}^{'}=2*\sqrt{\left ( \frac{R_{1}}{2} \right )^{2}+(2h)^{2}} }[/math]
For [math]\displaystyle{ R_{1} }[/math] y [math]\displaystyle{ R_{2} }[/math] the deduction and the distances are equals, therefore:
[math]\displaystyle{ R_{2}=R_{1} }[/math]
[math]\displaystyle{ R_{2}^{'}=R_{1}^{'} }[/math]
1.2. Antennas of Heights Equal Located in Any Point of the Street
As the direct ray LOS does not vary and has not angular variation between the rays, the distance of the first two rays [math]\displaystyle{ R_{0} }[/math] and [math]\displaystyle{ R_{0}^' }[/math] of model does not vary and deduced according to the mathematic model for two rays.[1] For the other four rays it applies the next mathematical process:
[math]\displaystyle{ R_{1} }[/math] is obtained through a geometric analysis of the top view for the model and it applies the Pythagorean Theorem triangles, taking into account the distance between the wall and the antennas [math]\displaystyle{ w_{t1} }[/math], [math]\displaystyle{ w_{r1} }[/math], [math]\displaystyle{ w_{t2} }[/math], [math]\displaystyle{ w_{r2} }[/math] are different:
[math]\displaystyle{ R_{1}=\sqrt{d^{2}-(w_{t1}-w_{r2})^{2}+(w_{t1}+w_{t2}-w_{r2})^{2}} }[/math]
For likeness of triangles in the top view for model is determined the equation [math]\displaystyle{ R_{1} }[/math]:
[math]\displaystyle{ d^{'}=\sqrt{d^{2}-(w_{t1}-w_{r2})^{2}} }[/math]
[math]\displaystyle{ x=\frac{(w_{r2}*R_{1}}{w_{r2}+w_{t2}+w_{t1}-w_{r2}} }[/math]
[math]\displaystyle{ R_{1}^{'}=\sqrt{(R_{1}-x^){2}+(2*h)^{2}}+\sqrt{(x)^{2}+(2*h)^{2}} }[/math]
For [math]\displaystyle{ R_{1} }[/math] and [math]\displaystyle{ R_{2} }[/math] the deduction and the distances are equal then:
[math]\displaystyle{ R_{2}=R_{1} }[/math]
[math]\displaystyle{ R_{2}^{'}=R_{1}^{'} }[/math]

1.3. Antennas of Heights Different Located in the Center of the Street
For antennas of different heights with rays that rebound in the wall, it is noted that the wall is the half point, where the two transmitted rays they fall on such wall. This wall has half the height between the height of the [math]\displaystyle{ T_{X} }[/math] and [math]\displaystyle{ R_{X} }[/math], it means smaller than the transmitter and higher than the receiver and this high is where the two rays impact in the point, then rebound to the receiver. The ray reflected leaves two reflections, one that it has the same high of the wall and the other the receiver, and the ray of the line of sight maintains the same direction between the [math]\displaystyle{ T_{X} }[/math] and the [math]\displaystyle{ R_{X} }[/math]. The diagonal distance d´ that separates the two antennas divides in two distances through of the wall, one is called [math]\displaystyle{ a }[/math] and the other [math]\displaystyle{ d-a }[/math].[2]
1.4. Antennas of Heights Different Located in any Point of the Street
For the mathematical model of six-ray propagation for antennas of different heights located at any point in the street, [math]\displaystyle{ h_{t}\neq h_{r} }[/math], there is a direct distance [math]\displaystyle{ d }[/math] that separates the two antennas, the first ray is formed by applying The Pythagorean theorem from the difference of heights of the antennas with respect to the line of sight:
[math]\displaystyle{ R_{0}=\sqrt{(d)^{2}+(h_t-h_r)^{2}} }[/math]

The second ray or reflected ray is calculated as the first ray but the heights of the antennas are added to form the right triangle.
[math]\displaystyle{ R_{0}^{'} =\sqrt{(d)^{2}+(h_t+h_r)^{2}} }[/math]
For deducing the third ray it is calculated the angle between the direct distance [math]\displaystyle{ d }[/math] and the distance of line of sight [math]\displaystyle{ R_{0} }[/math]
[math]\displaystyle{ \cos\theta=\frac{h_t-h_r}{R_{0}} }[/math]
Now deducing the height that subtraction of the wall with respect the height of the receiver called [math]\displaystyle{ z }[/math] by similarity the triangles:
[math]\displaystyle{ \frac{z}{a}=\frac{h_t}{d^{'}} }[/math]
[math]\displaystyle{ z=\frac{h_t*~a}{d^{'}} }[/math]
By similarity of triangles it can deduce the distance where the ray hits the wall until the perpendicular of the receiver called a achieved:
[math]\displaystyle{ \frac{a}{w^{t2}}=\frac{d^{'}}{w_{t1}+w_{r1}} }[/math]
[math]\displaystyle{ a=\frac{d^{'}*w_{t2}}{\left(w_{t1}+w_{r1}\right)} }[/math]
[math]\displaystyle{ R_{1}=\frac{\sqrt{(h_t-h_r-z)^{2}+(d^{'}-a)^{2}}+\sqrt{z^{2}+a^{2}}}{\cos\theta} }[/math]
By similarity of the triangles can be deduced the equation of the fourth ray:
[math]\displaystyle{ R_{1}^{'} =\frac{\sqrt{(h_t+h_r+z)^{2}+(d^{'}-a)^{2}}+\sqrt{(2h_r+z)^{2}+a^{2}}}{\cos\theta} }[/math]
For [math]\displaystyle{ R_{1} }[/math] y [math]\displaystyle{ R_{2} }[/math] the deduction and the distances are equal, therefore:
[math]\displaystyle{ R_{2}=R_{1} }[/math]
[math]\displaystyle{ R_{2}^{'}=R_{1}^{'} }[/math]
2. Free-space Path Loss on the Model

Consider a transmitted signal in the free space a receptor located a distance d of the transmitter. One may add rays bouncing off each side of a street in an urban corridor, leading to a six-rays model, with rays [math]\displaystyle{ R_{0} }[/math], [math]\displaystyle{ R_{1} }[/math] and [math]\displaystyle{ R_{2} }[/math] each one having a direct and a ground bouncing ray.[3]
An important assumption must be made to simplify the model: [math]\displaystyle{ T }[/math] is small compared to the symbol length of the useful information, that is [math]\displaystyle{ s(t)=s(t-T) }[/math]. For the rays rebound outside the earth and on each side of the street, this assumption is fairly safe, but in general will have remembered that these assumptions mean the dispersion of delays (diffusion of the values [math]\displaystyle{ T }[/math]) is smaller than symbols speed of transmission.
Free-space path loss of six rays model is defined as:
[math]\displaystyle{ p_{0}(t)=\sqrt{(G_iG_r)}\frac{\lambda}{4\pi}\left(\frac{\exp(j*2\pi*R_{0}/{\lambda})}{R_{0}}+\Gamma\frac{\exp(j*2\pi*R_{0}^{'}/{\lambda})}{R_{0}^{'}}\right) }[/math]
[math]\displaystyle{ p_{1}(t)=\sqrt{(G_iG_r)}\frac{\lambda}{4\pi}~\Gamma_{1}\left(\frac{\exp(j*2\pi*R_{1}/{\lambda})}{R_{1}}+\Gamma\frac{\exp(j*2\pi*R_{1}^{'}/{\lambda})}{R_{1}^{'}}\right) }[/math]
[math]\displaystyle{ p_{2}(t)=\sqrt{(G_iG_r)}\frac{\lambda}{4\pi}~\Gamma_{1}\left(\frac{\exp(j*2\pi*R_{2}/{\lambda})}{R_{2}}+\Gamma\frac{\exp(j*2\pi*R_{2}^{'}/{\lambda})}{R_{2}^{'}}\right) }[/math]
[math]\displaystyle{ P_l~(dB)=20\log\left|~\sum_{i=0}^{N}P_i~\right| }[/math]
[math]\displaystyle{ {\lambda}= }[/math] [math]\displaystyle{ {c \over f} }[/math] is the wavelength.
[math]\displaystyle{ T= }[/math] Is the time difference between the two paths.
[math]\displaystyle{ \Gamma = }[/math] Is the coefficient of ground reflection.
[math]\displaystyle{ G_i= }[/math] Gain of the transmitter.
[math]\displaystyle{ G_r= }[/math] Receiver gain.
References
- T.Rappaport (2002). Wireless Communications: Principles and Practice. Upper Saddle River, N.J.: Prentice Hall.. ISBN 978-0137192878. https://archive.org/details/smartantennasfor00jose.
- A. J. Rustako, Jr., Noach Amitay, G. J. Owens, R.S. Roman. (1991). Radio Propagation at Microwave Frequencies for Line-of-Sight Microcellular Mobile and Personal Communications..
- Schwengler, Thomas (2016). Wireless & Cellular Communications Class Notes for TLEN-5510-Fall.. Universidad de Colorado.. pp. http://morse.colorado.edu/~tlen5510/text/classwebch3.html.+"Chapter 3: Radio Propagation Modeling"




