You're using an outdated browser. Please upgrade to a modern browser for the best experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Ilaria Fiore | -- | 3838 | 2022-09-21 17:05:10 | | | |
| 2 | Rita Xu | Meta information modification | 3838 | 2022-09-22 02:58:18 | | | | |
| 3 | Rita Xu | + 4 word(s) | 3842 | 2022-09-23 10:33:08 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Greco, A.; Caddemi, S.; Caliò, I.; Fiore, I. Elastic Beam-like Model of Multi-Storey Framed Buildings. Encyclopedia. Available online: https://encyclopedia.pub/entry/27447 (accessed on 25 December 2025).
Greco A, Caddemi S, Caliò I, Fiore I. Elastic Beam-like Model of Multi-Storey Framed Buildings. Encyclopedia. Available at: https://encyclopedia.pub/entry/27447. Accessed December 25, 2025.
Greco, Annalisa, Salvatore Caddemi, Ivo Caliò, Ilaria Fiore. "Elastic Beam-like Model of Multi-Storey Framed Buildings" Encyclopedia, https://encyclopedia.pub/entry/27447 (accessed December 25, 2025).
Greco, A., Caddemi, S., Caliò, I., & Fiore, I. (2022, September 21). Elastic Beam-like Model of Multi-Storey Framed Buildings. In Encyclopedia. https://encyclopedia.pub/entry/27447
Greco, Annalisa, et al. "Elastic Beam-like Model of Multi-Storey Framed Buildings." Encyclopedia. Web. 21 September, 2022.
Copy Citation
Modern computational techniques have greatly influenced the numerical analyses of structures, not only in terms of calculation speed, but also in terms of procedural approach. In particular, great importance has been given to structural modelling, that is, the process by which a structure and the actions to which it is subjected are reduced to a simplified scheme. The use of a simplified calculation scheme is necessary since the structures are, in general, considerably complex physical systems whose behaviour is influenced by a large number of variables.
modelling of framed structures
multi-storey buildings
beam-like models
elastic models
1. Introduction
The evaluation of the dynamic response of multi-storey buildings, particularly when subjected to seismic loading, has represented one of the most important tasks of structural engineering research studies in the last century, and is still the objective of studies and improvements. The advancements in computational procedures and parallel processing in the recent years have enhanced the accurate dynamic analysis and seismic vulnerability of multi-storey buildings. These analyses can be carried out at the building or urban level; simplified or high-fidelity models, as well as approximate or sophisticated large-scale simulations, are currently adopted. However, when analysing entire urban areas or when performing several simulations aiming to provide sufficient data for expressing probability failure maps, a convenient balance between accuracy and computational burden is needed. In this precise context, beam-like models play an important role.
Analyses developed by means of three-dimensional (3D) numerical models aim to provide an accurate representation of the main characteristics of the dynamic behaviour of real structures and, for this reason, must be detailed and based on reliable data. Therefore, a rigorous and accurate evaluation of the dynamic response of a multi-storey building subjected to seismic excitation requires adequate structural expertise and great computational burden. On the other hand, the need for a sufficiently accurate seismic vulnerability assessment of a large number of existing buildings in seismic areas, in particular at an urban scale, has stimulated a significantly increased interest in simplified but sufficiently accurate models able to represent multi-storey buildings.
Since multi-storey buildings may exhibit a great number of degrees of freedom, especially if several deformability parameters of the structural members are taken into account, simplified multi-degree-of-freedom (MDOF) models are usually considered. In this regard, some models have been presented in the scientific literature for the simulation of linear as well as non-linear dynamic responses of multi-storey buildings. The most important goal of these simplified models is to reduce the number of degrees of freedom of the 3D model, preserving the main features of its dynamic response.
A new and renovated interest has recently grown in beam-like models, which were introduced in the last century. Beam-like models, which are based on the equivalence of multi-level structures to flexural–shear coupling continuum beams, aim to simulate the dynamic behaviour of multi-level buildings and meanwhile reduce the computational burden. Several authors have demonstrated interest in beam-like models and proposed suitable simplified approaches for the dynamic analysis of multi-storey structures.
2. Elastic Beam-like Models of Multi-Storey Framed Buildings
The analysis of multi-storey buildings has been performed in recent decades by means of equivalent beam-like models. These models are represented by continuum mono-dimensional elements whose static and dynamic responses are strictly related to the assumed hypotheses concerning their geometry, their deformability, the material behaviour and the kind of developed analysis (linear or non-linear).
Most of the studies in the scientific literature concerning beam-like models deal with elastic behaviour. Each of these models aim to reproduce the static or dynamic response of complex structures, taking into account their prevailing elastic deformability. Therefore, different beam-like models having shear-only, flexural-only or coupled shear–flexural deformability are reviewed and discussed below. Some beam-like models are equivalent to plane structures, whilst others are able to represent the three-dimensional behaviour of a building. The presence of twisting effects may or may not be considered. All these characteristics of the beam-like models lead to different choices of the degrees of freedom in order to define a system able to reproduce the investigated behaviour with the established kinematics. The approaches also differ in the assumption hypothesis about the mass of the models which can be concentrated or distributed along the beam.
The main advantage of some beam-like models present in the literature is their adoption for the study of the static or dynamic behaviour of real buildings, as shown in the applicative section of the following cited papers. Furthermore, beam-like models can be base-isolated systems or include soil–structure interaction by means of an appropriate modelling of the base restraints.
Several classifications can be made in the attempt to illustrate the great number of scientific contributions in this field. In the following, researchers choose to classify the scientific literature by separating the models of a single equivalent beam from those in which beams with different characteristics are coupled to each other, or in which single beams are coupled to walls or frames. For the first category, a further distinction will be made between planar and three-dimensional systems.
The adopted classification has been graphically illustrated in Figure 1.
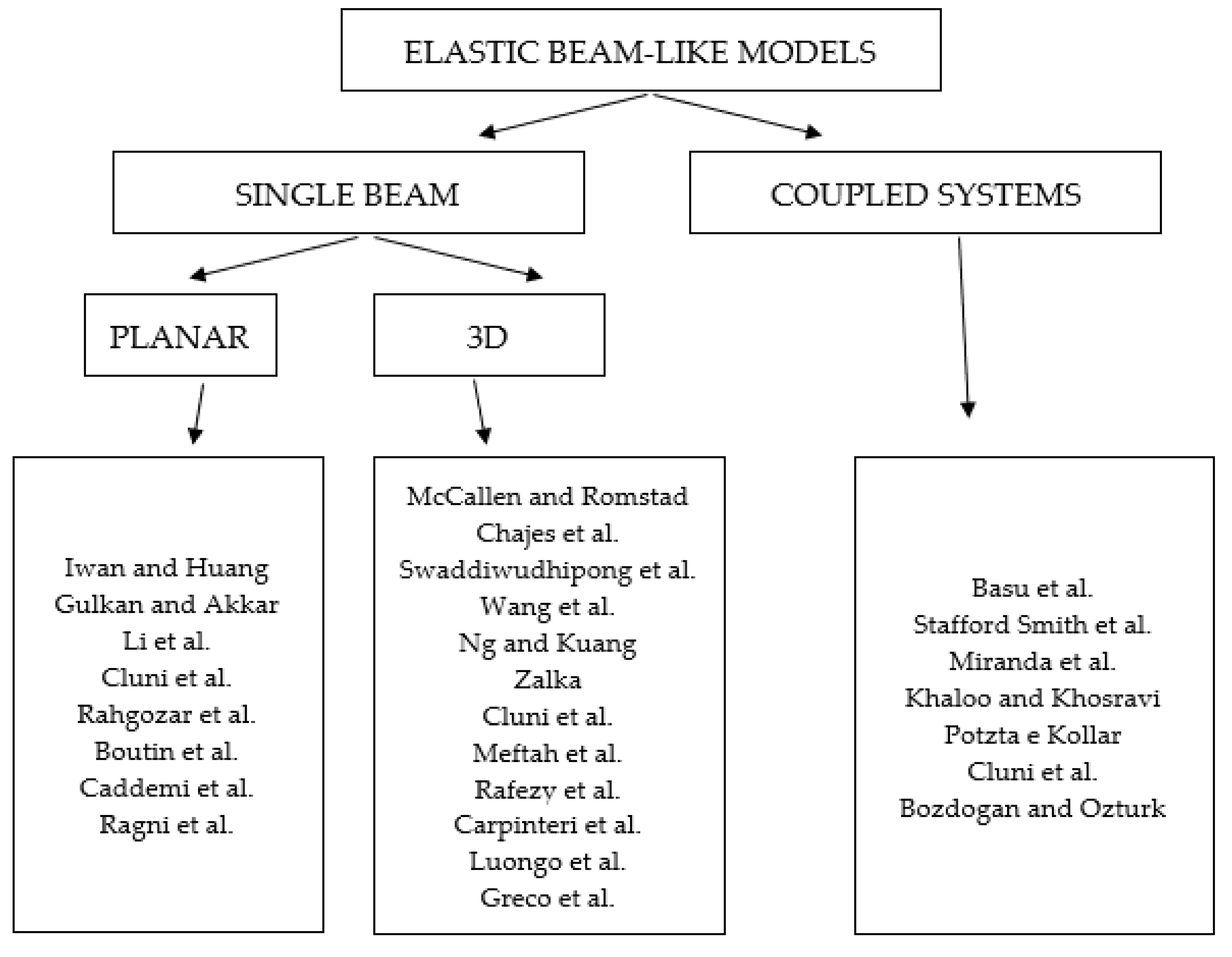
Figure 1. Classification of elastic beam-like models.
2.1. Single Beams
2.1.1. Planar Systems
Among the studies concerning planar beam-like structures presented in the scientific literature in the last 50 years, one of the first ones was developed by Iwan [1] and Huang [2], who proposed a continuous uniform shear–beam model to predict elastic storey drift demand on structures due to near-field earthquake ground motions. Noticing that the continuous model predicts the inter-storey drifts more accurately than an equivalent single-degree-of-freedom (SDOF) system, they suggested the use of a drift spectrum instead of the well-known response spectrum.
The evaluation of the maximum inter-storey drifts of a building by means of the first-mode shape of a uniform shear beam was the aim of a later study proposed by Gulkan and Akkar [3]. In 2005, they modified the equivalent shear beam model in order to take into account the general moment-resisting frame (MRF) behaviour of the structure by introducing some empirical coefficients into the maximum ground storey and inter-storey drift expressions [4].
Beam-like structures, due to their inherent characteristics, have great application in modelling tall buildings. The in-plane free vibration of tall buildings was studied in 2000 by Li et al. [5] by means of an equivalent flexural multi-step cantilever beam with stiffness, mass and axial loads distributed according to a power or exponential law of variation. The approximated solution of this complex problem was obtained using the exact solution of a one-step bar with a variable cross-section together with the transfer matrix method. This approach was extended in [6] by Rahgozar et al. for an equivalent Timoshenko multi-step beam, and in [7] for a sandwich beam, the latter defined according to Zalka’s, Potza’s and Kollar’s approach described in the following.
Additionally, Cluni et al. adopted two equivalent beam models for studying the dynamic response of tall buildings under wind loads [8]. The equivalent beam models had uniform flexural and shear stiffness, linked together in series or in parallel. The equivalence criterion was based on the minimization of the difference of static and dynamic response features obtained by means of the equivalent beam and the FEM model. The mechanical parameters used to describe the beam varied sensibly with respect to the real ones, but the main interest was to find an equivalent beam which could accurately describe the response of the slender building, regardless of any physical meaning. In 2020, the model was extended in order to describe the flexural, shear and torsional behaviour of uniform tall buildings with an asymmetrical plan subjected to wind or earthquake loads [9]. The mechanical and dynamic features of the equivalent beam were first evaluated, imposing the equivalence of the deformation energy between the equivalent sandwich beam and the sub-structures of the tall building, and then calibrated by minimizing a function which takes into account natural frequencies and static displacements. The limitation of this model consists of its unsuitability in representing asymmetrical buildings. The results of the analyses performed on regular and symmetrical buildings with uniform stiffness distribution are shown in terms of natural frequencies and mode shapes and in terms of displacements under static or dynamic wind or earthquake loads.
Tall buildings were also modelled by means of an equivalent beam by Rahgozar et al. in 2010. Basing the study on previous research [10], they proposed a continuum model for predicting the stress distribution and the displacement profile for a combined system of different structural elements, but only under specific load patterns [11]. The model consisted of an equivalent uniform cantilever beam with flexural and shear deformability and rotational springs simulating the belt trusses (Figure 2). This model was applied to estimate the natural frequencies and mode shapes of the tall buildings [12][13], obtaining acceptable errors if compared to finite element models.
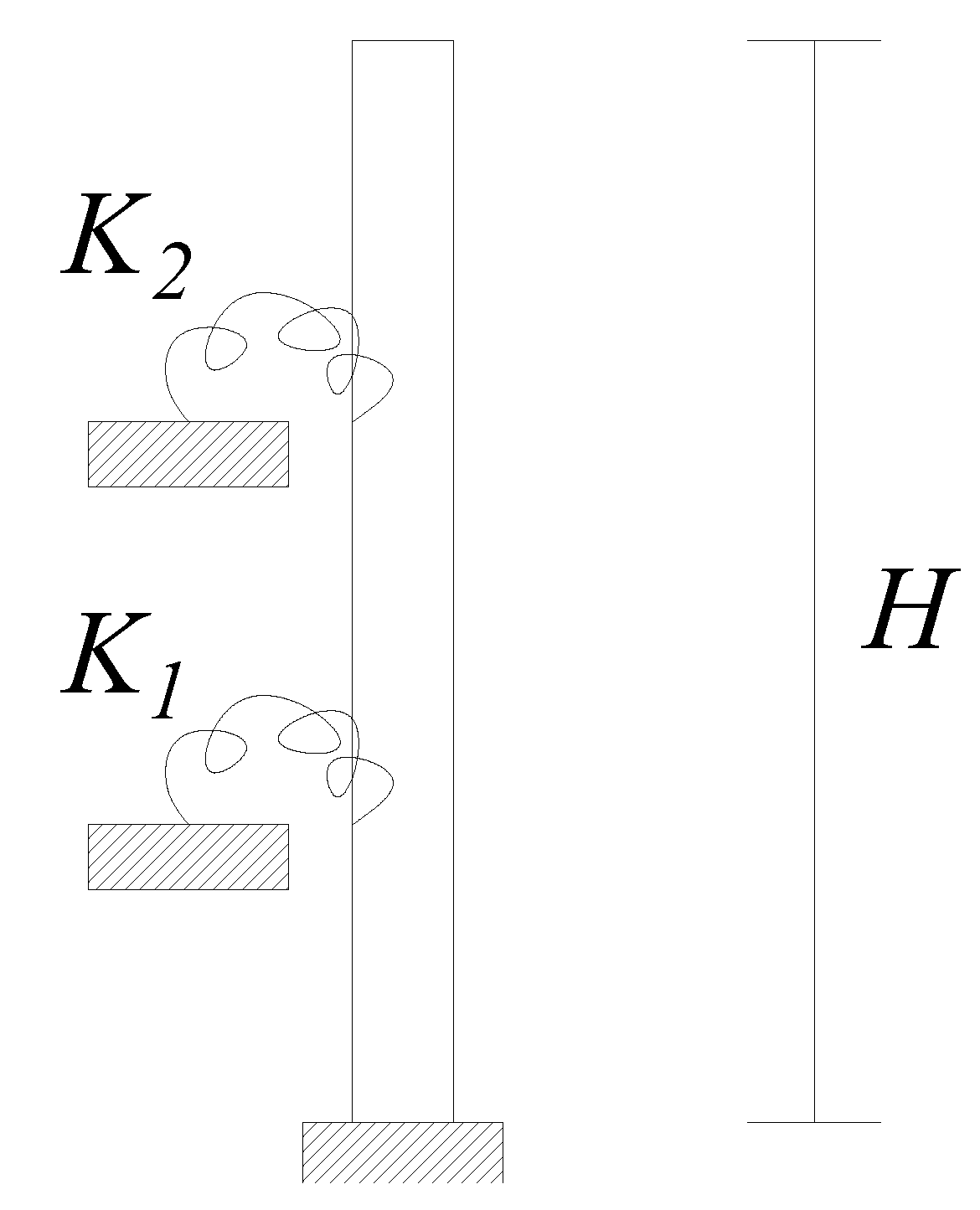
Figure 2. Schematization of the equivalent beam model proposed by Rahgozar et al.
Beam-like models have also been applied for the analysis of repetitive framed buildings. For example, in [14][15], Boutin et al. adopted the homogenization method of periodic discrete media (HPDM) for the analysis of repetitive reticular structures composed of interconnected elements (beams or plates) with the purpose of deducing the modal characteristics of the repetitive framed buildings. The homogenized continuum model can be defined as a shear-only beam, a Timoshenko beam, or a Euler–Bernoulli beam, and it provides the main structural characteristics. The first phase of the HPDM is the discretisation of the dynamic balance of the structure under harmonic vibrations, followed by the actual homogenisation procedure, through which a continuum model is elaborated from the discrete description. For the homogenization process, a scale parameter, measuring or the size of the basic cell of the structure or the characteristic size of deformation of the structure under vibrations, is introduced. Since this parameter has to be sufficiently small, the method is limited to the first frequencies and mode shapes, with wavelengths much larger than cell size. In [16], the continuum model obtained by means of the HPDM was adopted for studying the local resonance in reticulated frames.
The application of the HPDM is limited to periodic structures where the structural elements are slender enough to behave as Euler–Bernoulli beams. Franco et al. in [17] overcame this limitation by substituting an analytical part of the procedure with a numerical static analysis of a unit cell performed by means of a detailed finite element model. The authors state that this homogenization procedure can be applied to building structures if two fundamental conditions hold: periodicity and scale separation. The periodicity refers to the repetition of same-storey properties all along the building height whilst the scale separation ratio, which relates the height of one storey to the height of the entire building, must be sufficiently small. The beam-like model has been used to perform time–history analyses with natural seismic records of an existing 13-storey reinforced concrete frame building, namely, the Grenoble City Hall [18].
An important aspect in the beam characterization lies in the possibility of considering a variable cross-section in order to better simulate the non-uniform characteristics of the equivalent building.
Models of stepped Euler–Bernoulli or Timoshenko beams in the presence of deflection and rotation discontinuities along the span are presented by Caddemi et al. [19][20]. The proposed models rely on the adoption of Heaviside’s and Dirac’s delta distributions to model abrupt and concentrated—both flexural and shear—stiffness discontinuities of the beam that lead to exact closed-form solutions of the elastic response in the presence of static loads. Based on the latter solutions, a beam element suitable for the analysis of frame structures with an arbitrary distribution of singularities is proposed [19]. The exact explicit dynamic stiffness matrix of damaged frames structures is derived in [20], allowing the exact evaluation of the frequencies and the corresponding vibration modes, consistent with the distributed parameter model, through the application of the Wittrick–Williams’s algorithm.
Beam-like structures have also been adopted taking into account dissipative devices. For example, Ragni et al. [21] proposed a displacement-based method, particularly devoted to seismic design steel frames equipped with dissipative braces, by using an equivalent continuous beam-like model where flexural deformability and shear deformability are related, respectively, to columns and diagonals of the bracing system. The design method is appealing since analytical expressions of the required flexural and shear stiffness distributions are obtained and conveniently adopted in the preliminary design of dissipative diagonal braces and columns of steel frames.
2.1.2. Three-Dimensional Systems
One of the pioneering studies concerning the use of three-dimensional beam-like structures for the analysis of buildings has been provided by McCallen and Romstad. In [22][23], they proposed a simple uniform continuum model for the analysis of lattice structures (which are repetitive reticular structures). The equivalence between the lattice structure and the continuum model was established in terms of deformation energies for three assumed global deformation modes (axial, shear, bending). The continuum model was then analysed by means of a traditional finite element approach. Geometrical non-linearities are accounted for through updated Lagrangian coordinate transformation for each continuum finite element. The translational and rotational inertias are lumped at the end or midpoint nodes of the finite elements of the discretised continuum.
The approach was extended to three-dimensional buildings with rigid floors. Therefore, the global model has only three degrees of freedom, two orthogonal translations and one rotation at each floor level. By applying horizontal forces only, the rotational and axial degrees of freedom of the continuum can be condensed out. Later, the condensed continuum model of an individual frame can be transformed to global coordinates and added into the global stiffness (Figure 3).
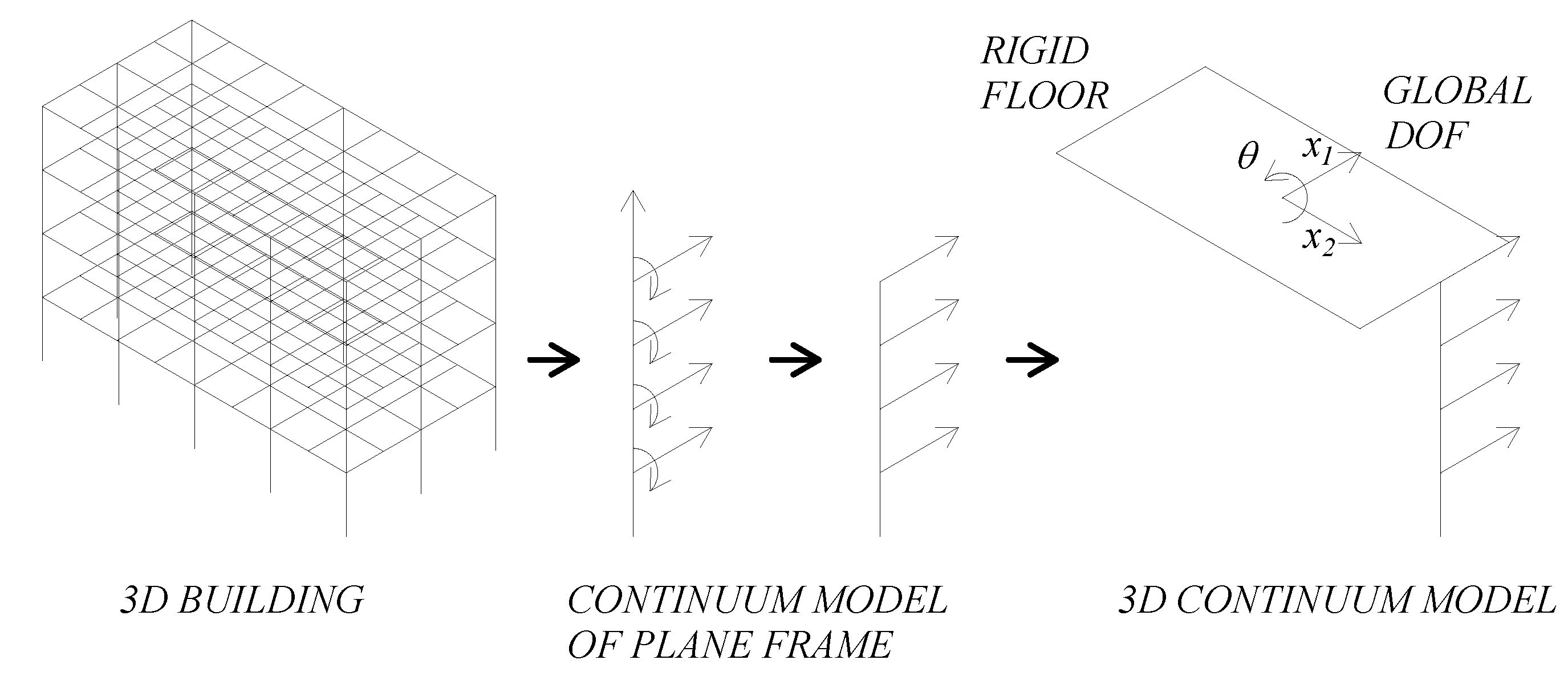
Figure 3. Construction of a 3D building model using continuum models for each plane frame according to McCallen and Romstad.
The continuum is used for the free vibration analysis of planar frames or buildings with uniform stiffness distribution along the height and the results are shown in terms of natural frequencies and mode shapes.
The previous study proposed by McCallen and Romstad inspired further developments. In particular, in 1993, Chajes et al. [24] extended the method to the determination of displacements and member forces in two-dimensional frames with reticular elements. In [25][26], the equivalent continuum model was applied to predict the measured seismic response of two existing buildings (a reinforced concrete one and a steel one) during the Loma Prieta earthquake (using the continuum model discretized with a number of finite elements equal to the number of floors).
Axial deformation of the equivalent beam-like model has been considered by Swaddiwudhipong et al. [27][28]. They proposed a uniform shear–flexural cantilever beam for 3D free vibration analysis of frame–core wall buildings. The solution in terms of natural frequencies and mode shapes is obtained using the Galerkin’s technique, adopting an exponential shape function.
Three-dimensional beam models are mandatory in order to take into account the torsional behaviour of buildings, and several researchers have focused their studies on this subject.
Among others, Wang et al. proposed an approximate method to estimate the first two periods of vibration of multi-storey uniform buildings with an asymmetrical plan [29]. The coupled natural frequencies of the multi-storey structure, due to the asymmetric distribution of the structural members with respect to the floor plan, were expressed in terms of uncoupled lateral frequency, uncoupled fundamental torsional-to-lateral frequency ratio and the eccentricity ratio. However, this approach is valid only for proportionate structural systems whose centres of stiffness lie on a vertical line.
Another study which deals with the application of three-dimensional equivalent beams for the evaluation of the torsional behaviour of buildings has been provided by Ng and Kuang [30][31]. In the cited references, they study the modal analysis for the coupled flexural–torsional vibration of asymmetric uniform tall buildings by means of an equivalent flexural–torsional cantilever, whose stiffness is determined as a simple sum of the stiffness of the vertical members. The equivalent beam can be coupled with a shear cantilever in order to take into account the shear deformability. However, further studies [32][33] have been limited to the free vibration analysis considering only an equivalent Euler–Bernoulli beam, or an equivalent shear cantilever beam, respectively.
Applying the concept of an “equivalent column”, Zalka proposed simple formulas in 2001 [34] for evaluating the natural three-dimensional frequencies of the buildings braced by frameworks, coupled shear walls, shear walls and cores. The method considered the local bending of the single vertical elements, the global bending of the frames/shear walls (associated with the axial deformation of the vertical elements) and shear deformations of the frames/shear walls (Figure 4). The pure torsional frequency is obtained by means of an analogy with respect to bending. Approximate formulas were provided to account for the interaction between translational and torsional modes for non-symmetrical buildings. The equivalent column was applied for the analysis of regular buildings with double planar symmetry and in-plane rigid floors. The same author proposed approximated closed-form solutions for studying tall buildings subjected to uniformly distributed static horizontal loads for both symmetrical [35] and non-symmetrical [36] systems in 2009 and 2014, respectively.
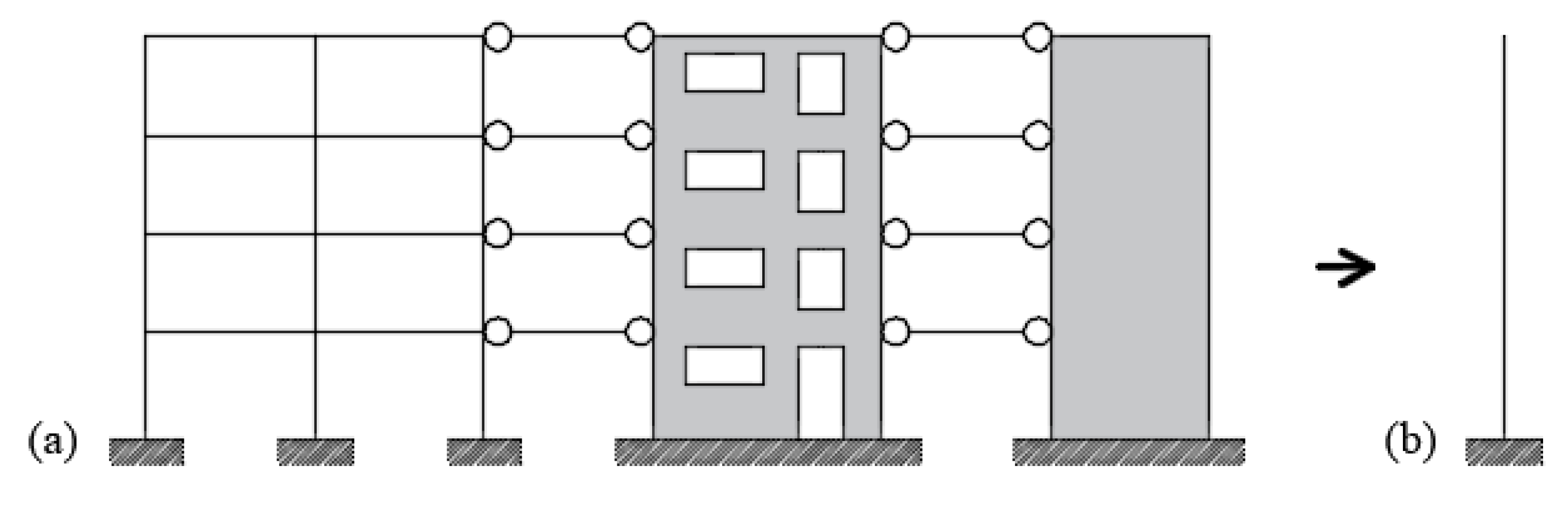
Figure 4. Model for lateral vibration analysis according to Zalka: (a) bracing system consisting of frames, coupled shear walls, shear walls and cores; (b) equivalent column.
In [37][38], Meftah et al. propose an approximate hand method for the seismic analysis of an asymmetric building structure with constant properties along its height, stiffened by a combination of shear walls and thin-wall open-section structures. The governing equations of free vibration of the equivalent flexural–torsional cantilever are derived on the base of the continuum method and D’Alembert principle, and the solution is determined by applying Galerkin’s technique in [37], or an analytical method in [38]. The internal forces of the building subjected to an earthquake are also derived using the acceleration response spectrum and combining the modal responses by means of the square root of sum of squares (SRSS) method.
In addition to taking into account torsional effects, due to asymmetric building plans, some beam-like structures are also able to reproduce non-uniform stiffness distribution along the height. This result can be achieved by opportunely dividing the beam in different segments representing the building inter-storeys.
With this aim in [39] and in [40], Rafezy et al. propose a stepped shear–torsional cantilever model and a stepped Timoshenko cantilever model, respectively, for the calculation of the natural frequencies of an asymmetric three-dimensional frame or wall–frame structures by means of the Wittrick–Williams algorithm. Each beam segment is representative of a number of uniform storeys, variable from one to the total number of storeys of the building in the case this is uniform throughout its height. The stiffness of each beam segment is calculated as the sum of the stiffness of each frame in the considered direction with reference to the corresponding storeys. The equations of motion refer to each beam segment of the original, asymmetric, three-dimensional wall–frame structure. The entire original structure can then be modelled by assembling the substitute beams corresponding to each segment in the usual way.
The variation in the stiffness at each inter-storey of the considered building is also considered in the construction of an equivalent beam-like model by Carpinteri et al. They propose an equivalent shear–torsional beam model for estimating the response of tall buildings under static horizontal loads in the initial design phase [41]. The equivalent shear beam has the stiffness of each inter-storey segment equal to the sum of stiffness of the columns of the corresponding floor and is subjected to elastic rotational springs simulating the stiffness of the floor slabs and to horizontal springs simulating the diagonal bracings (Figure 5). Therefore, the model is able to consider a non-uniform stiffness distribution. With N being the number of floors of the building, the total number of degrees of freedom is 3N: two translations and one rotation for each floor. The results are shown in terms of displacements and internal forces due to static wind loads. In [42][43], the model was extended in order to consider second-order torsional effects (Vlasov’s theory), allowing the computation of the natural frequencies and mode shapes of a uniform building by means of the equivalent beam with shear and torsional deformability.
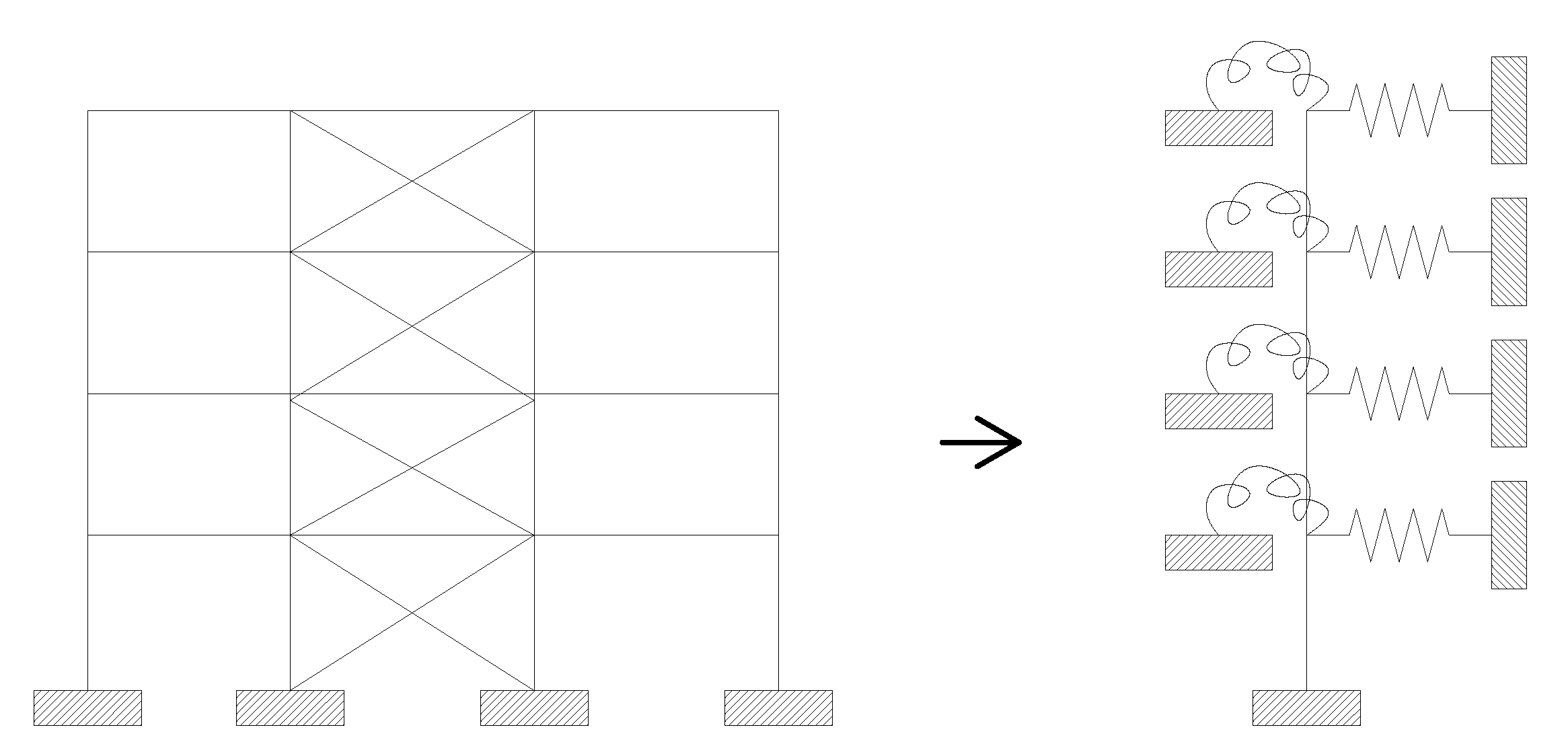
Figure 5. Model of a braced frame equivalent to a shear wall according to Carpinteri et al.
An equivalent beam model, deformable in shear and torsion and capable of approximately reproducing the dynamic behaviour of the three-dimensional shear-type structures, was introduced by a research team coordinated by Luongo [44][45], and its aeroelastic instability to wind excitation was analysed [46][47]. The homogenization process is based on the equivalence of the strain energy of the building cell with the corresponding beam segment. The model was used for the modal analysis of periodic buildings with symmetrical and asymmetrical plans. The model was also adopted in other papers in 2019 [48][49] for studying the linear and non-linear elastic behaviour of periodic tower buildings under the assumption that the beam is internally constrained, so that it is capable of experiencing shear strains and torsion only. The elasto-geometric and inertial characteristics of the beam are directly identified from a discrete model of a three-dimensional frame via a homogenization process. A more refined Timoshenko beam-like model suitable for the dynamic analysis of periodic buildings has recently been proposed [50]. The homogenization process is still based on the equivalence of the strain energy of the building cell, between two rigid floors with structural elements such as columns and shear walls, and the corresponding beam segment. In [51][52][53], the classical rigid-floor assumption is overcome in the calibration procedure, which is based on FE analysis results, by means of the introduction of opportune correction coefficients that take into account the out-of-plane floor deformability due to the shear–torsional behaviour. The results of the analyses performed on buildings with uniform stiffness distribution are shown in terms of natural frequencies, mode shapes, lateral displacements and axial forces of the structural elements under static loads. The model can also be adopted for the buckling analysis [54], taking into account the soil–structure interaction, and for studying the dynamic response [55][56] of tower buildings. A summary of the study of these latter models and their various applications is reported in [57].
A contribution to the evaluation of the elastic response of non-uniform buildings by means of equivalent beam-like models is also given by the present authors in [58]. In the cited study, researchers presented a 3D shear–torsional cantilever beam suitable for the schematization of real buildings that do not have a uniform mass and stiffness distribution along their height and are characterised by unsymmetrical plans causing not negligible torsional effects (Figure 6). The equivalent beam has a non-uniform stepwise cross-section and each portion represents a building inter-storey whose shear and torsional stiffness are initially approximately evaluated according to a geometrical consistent reference model. Stiffness contributions due to the beams and floors of the building can be neglected (rigid floor hypothesis) or considered by means of appropriate stiffness reduction coefficients. The linear dynamic behaviour of the non-uniform beam-like element is evaluated by discretizing the continuous model according to a Rayleigh–Ritz approach based on an appropriate number of modal shapes of a uniform beam having only shear and torsional deformability.
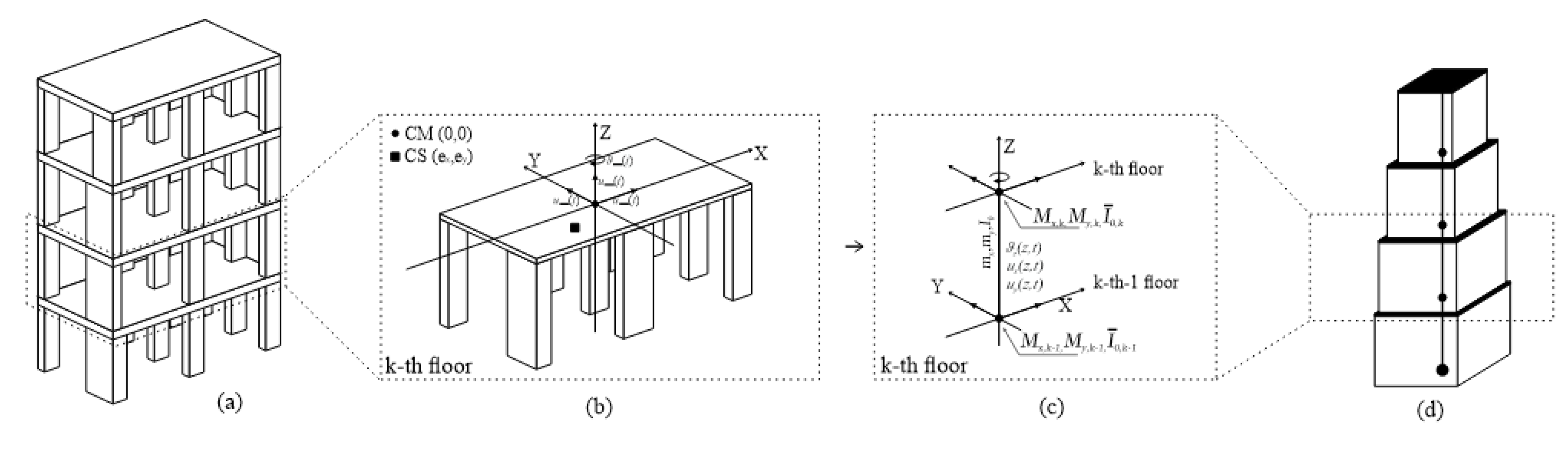
Figure 6. Concept of representation starting from (a) the 3D structure and (b) the generic k-th floor (or inter-storey) up to the (c) sub-beam element and the (d) proposed beam-like model. Source: own figure [58].
References
- Iwan, W.D. Drift spectrum: Measure of demand for earthquake ground motions. J. Struct. Eng. 1997, 123, 397–404.
- Huang, C.T. Considerations of multimode structural response for near-field earthquakes. J. Eng. Mech. 2003, 129, 458–467.
- Gulkan, P.; Akkar, S. A simple replacement for the drift spectrum. Eng. Struct. 2002, 24, 1477–1484.
- Akkar, S.; Yazgan, U.; Gulkan, P. Drift estimates in Frame Buildings Subjected to Near-Fault Ground Motions. J. Struct. Eng. 2005, 131, 1014–1024.
- Li, Q.S.; Fang, J.Q.; Jeary, A.P. Free vibration analysis of cantilevered tall structures under various axial loads. Eng. Struct. 2000, 22, 525–534.
- Rahgozar, R.; Safari, H.; Kaviani, P. Free vibration of tall buildings using Timoshenko beams with variable cross-section. In Structures under Shock and Impact VIII; WIT Press: Southampton, UK, 2004; pp. 233–242.
- Kaviani, P.; Rahgozar, R.; Saffari, H. Approximate analysis of tall buildings using sandwich beam models with variable cross section. Struct. Des. Tall Spec. Build. 2008, 17, 401–418.
- Cluni, F.; Gioffrè, M.; Gusella, V. Dynamic response of tall buildings to wind loads by reduced order equivalent shear-beam models. J. Wind Eng. Ind. Aerodyn. 2013, 123 Pt B, 339–348.
- Gioffrè, M.; Cluni, F.; Gusella, V. Characterization of an Equivalent Coupled Flexural-Torsional Beam Model for the Analysis of Tall Buildings under Stochastic Actions. J. Struct. Eng. 2020, 146, 04020239-1.
- Kwan, A. Simple method for approximate analysis of framed tube structures. J. Struct. Eng. ASCE 1994, 120, 1221–1239.
- Rahgozar, R.; Ahmadi, A.; Sharifi, Y. A simple mathematical model for approximate analysis of tall buildings. Appl. Math. Model. 2010, 34, 2437–2451.
- Malekinejad, M.; Rahgozar, R. A simple analytic method for computing the natural frequencies and mode shapes of tall buildings. Appl. Math. Model. 2012, 36, 3419–3432.
- Malekinejad, M.; Rahgozar, R. An analytical model for dynamic response analysis of tubular tall buildings. Struct. Des. Tall Spec. Build. 2014, 23, 67–80.
- Boutin, C.; Hans, S. Homogenisation of periodic discrete medium: Application to dynamics of framed structures. Comput. Geotech. 2003, 30, 303–320.
- Hans, S.; Boutin, C. Dynamics of discrete framed structures: A unified homogenized description. J. Mech. Mater. Struct. 2008, 3, 1709–1739.
- Chesnais, C.; Boutin, C.; Hans, S. Effects of the local resonance in bending on the longitudinal vibrations of the reticulated beams. Wave Motion 2015, 57, 1–22.
- Franco, C.; Chesnais, C.; Semblat, J.-F.; Giry, C.; Desprez, C. Finite element formulation of a homogenized beam for reticulated structure dynamics. Comput. Struct. 2022, 261–262, 106729.
- Franco, C.; Chesnais, C.; Semblat, J.-F.; Desprez, C.G.C. Seismic analysis of tall buildings through an enriched equivalent beam model: Application to Grenoble City Hall. In Proceedings of the 3rd European Conference on Earthquake Engineering & Seismology, Bucharest, Romania, 4–9 September 2022.
- Caddemi, S.; Caliò, I.; Cannizzaro, F.; Rapicavoli, D. A novel beam finite element with singularities for the dynamic analysis of discontinuous frames. Arch. Appl. Mech. 2013, 83, 1451–1468.
- Caddemi, S.; Caliò, I. The exact explicit dynamic stiffness matrix of multi-cracked Euler-Bernoulli beam and applications to damaged frame structures. J. Sound Vib. 2013, 332, 3049–3063.
- Ragni, L.; Zona, A.; Dall’Asta, A. Analytical expressions for preliminary design of dissipative bracing systems in steel frames. J. Constr. Steel Res. 2011, 67, 102–113.
- McCallen, D.; Romstad, K.M. Application of a Continuum Model in Building Analysis. In Proceedings of the “Buildings Structures” Proceedings Structures Congress ‘87, Orlando, FL, USA, 17–20 August 1987.
- McCallen, D.B.; Romstad, K.M. A continuum model for the nonlinear analysis of beam-like lattice structures. Comput. Struct. 1988, 29, 177–197.
- Chajes, M.; Romstad, K.; McCallen, D. Analysis of multiple-bay frames using continuum model. J. Struct. Eng. ASCE 1993, 119, 522–546.
- Chajes, M.; Finch, W.; Kirby, J. Dynamic analysis of a ten-story reinforced concrete building using a continuum model. Comput. Struct. 1996, 58, 487–498.
- Chajes, M.; Zhang, L.; Kirby, J. Dynamic analysis of tall building using reduced-order continuum model. J. Struct. Eng. ASCE 1996, 122, 1284–1291.
- Swaddiwudhipong, S.; Lee, S.-L.; Zhou, Q. Effect of axial deformation on vibration of tall buildings. Struct. Des. Tall Build. 2001, 10, 79–91.
- Swaddiwudhipong, S.; Soelarno Sidji, S.; Lee, S.-L. The effects of axial deformation and axial force on vibration characteristics of tall buidings. Struct. Des. Tall Build. 2002, 11, 309–328.
- Wang, Y.; Arnaouti, C.; Guo, S. A simple approximate formulation for the first two frequencies of asymmetric wall-frame multi-storey building structures. J. Sound Vib. 2000, 236, 141–160.
- Ng, S.; Kuang, J.S. Triply coupled vibration of asymmetric wall-frame structures. J. Struct. Eng. 2000, 126, 982–987.
- Kuang, J.S.; Ng, S. Dynamic coupling of asymmetric shear wall structures: An analytical solution. Int. J. Solids Struct. 2001, 38, 8723–8733.
- Kuang, J.S.; Ng, S. Coupled vibration of tall building structures. Struct. Des. Tall Spec. Build. 2004, 13, 291–303.
- Kuang, J.S.; Ng, S. Lateral shear-St. Venant torsion coupled vibration of asymmetric-plan frame structures. Struct. Des. Tall Spec. Build. 2009, 18, 647–656.
- Zalka, K. A simplified method for calculation of the natural frequencies of wall-frame buildings. Eng. Struct. 2001, 23, 1544–1555.
- Zalka, K. A simple method for the deflection analysis of tall wall-frame building structures under horizontal load. Struct. Des. Tall Spec. Build. 2009, 18, 291–311.
- Zalka, K. Maximum deflection of asymmetric wall-frame buildings under horizontal load. Period. Polytech. Civ. Eng. 2014, 58, 387–396.
- Meftah, S.A.; Tounsi, A.; El Abbas, A.B. A simplified approach for seismic calculation of a tall building braced by shear wall and thin-walled open section structures. Eng. Struct. 2007, 29, 2576–2585.
- Meftah, S.A.; Tounsi, A. Vibration charateristics of tall buildings braced by shear walls and thin-walled open section structures. Struct. Des. Tall Spec. Build. 2008, 17, 203–216.
- Rafezy, B.; Zare, A.; Howson, W.P. Coupled lateral-torsional frequencies of asymmetric, three-dimensional frame structures. Int. J. Solids Struct. 2007, 44, 128–144.
- Rafezy, B.; Howson, W.P. Vibration analysis of doubly asymmetric, three-dimensional structures comprising wall and frame assemblies with variable cross-section. J. Sound Vib. 2008, 318, 247–266.
- Carpinteri, A.; Lacidogna, G.; Cammarano, S. Structural analysis of high-rise buildings under horizontal loads: A study on the Intesa Sanpaolo Tower in Turin. Eng. Struct. 2013, 56, 1362–1371.
- Carpinteri, A.; Lacidogna, G.; Nitti, G. Open and closed shear-walls in high-rise structural systems: Static and dynamic analysis. Curved Layer. Struct. 2016, 3, 154–171.
- Nitti, G.; Lacidogna, G.; Carpinteri, A. Structural analysis of high-rise buildings under horizontal loads: A study on the Piedmont Region Headquarters tower in Turin. Open Constr. Build. Technol. J. 2019, 13, 81–96.
- Piccardo, G.; Tubino, F.; Luongo, A. A shear-shear torsional beam model for nonlinear aeroelastic analysis of tower buildings. J. Appl. Math. Phys. 2014, 66, 1895–1913.
- Sciomenta, M.; Luongo, A. Linear dynamic analysis of multistore tower buildings via an equivalent shear-shear torsional beam model. In Proceedings of the XXIII Conference of the Italian Association of Theoretical and Applied Mechanics, Salerno, Italy, 4–7 September 2017.
- Piccardo, G.; Tubino, F.; Luongo, A. Equivalent nonlinear beam model for the 3-D analysis of shear-type buildings: Application to aeroelastic instability. Int. J. Non-Linear Mech. 2015, 80, 52–65.
- Di Nino, S.; Luongo, A. Nonlinear aeroelastic behaviour of a base-isolated beam under steady wind flow. Int. J. Non-Linear Mech. 2020, 119, 103340.
- D’Annibale, F.; Ferretti, M.; Luongo, A. Shear-shear-torsional homogenous beam models for nonlinear periodic beam-like structures. Eng. Struct. 2019, 184, 115–133.
- Luongo, A.; Zulli, D. Free and forced linear dynamics of a homogeneous model for beam-like structures. Meccanica 2020, 55, 907–925.
- Piccardo, G.; Tubino, F.; Luongo, A. Equivalent Timoshenko linear beam model for the static and dynamic analysis of tower buildings. Appl. Math. Model. 2019, 71, 77–95.
- Ferretti, M.; D’Annibale, F.; Luongo, A. Modeling beam-like planar structures by a one-dimensional continuum: An analytical-numerical method. J. Appl. Comput. Mech. 2021, 7, 1020–1033.
- D’Annibale, F.; Ferretti, M.; Luongo, A. Static and Dynamic Responses of Micro-Structured Beams. Appl. Sci. 2020, 10, 6836.
- Luongo, A.; D’Annibale, F.; Ferretti, M. Shear and flexural factors for static analysis of homogenized beam models of planar frames. Eng. Struct. 2021, 228, 111440.
- Ferretti, M.; D’Annibale, F.; Luongo, A. Buckling of tower buildings on elastic foundation under compressive tip forces and self-weight. Contin. Mech. Thermodyn. 2020.
- Zulli, D.; Luongo, A. Nonlinear dynamics and stability of a homogeneous model of tall buildings under resonant action. J. Appl. Comput. Mech. 2021, 7, 1034–1048.
- Di Nino, S.; Luongo, A. Nonlinear dynamics of a base-isolated beam under turbulent wind flow. Nonlinear Dyn. 2022, 107, 1529–1544.
- Luongo, A. Statics, Dynamics, Buckling and Aeroelastic Stability of Planar Cellular Beams. In Modern Trends in Structural and Solid Mechanics 2: Vibrations; ISTE, Ltd.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2021; pp. 143–165.
- Greco, A.; Fiore, I.; Occhipinti, G.; Caddemi, S.; Spina, D.; Caliò, I. An Equivalent Non-Uniform Beam-Like Model for Dynamic Analysis of Multi-Storey Irregular Buildings. Appl. Sci. 2020, 10, 3212.
More
Information
Subjects:
Engineering, Civil
Contributors
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
1.1K
Revisions:
3 times
(View History)
Update Date:
23 Sep 2022
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




