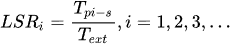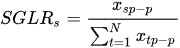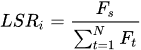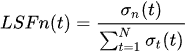1. Introduction
Planetary gear sets have played an undeniable role in power transmission systems for more than a century and have been the subject of extensive research
[1]. The advantages of planetary gears over the fix-axis gearbox include high power density, high speed reductions in compact spaces, multiple kinematic combinations, pure torsional reactions, and coaxial shafting
[2][3][4]. They are used in mining haul trucks, helicopters, aircraft engines, and some other types of heavy machinery
[4]. The load distribution on planets is a highly contentious subject that attracted researchers’ attention due to its remarkable and direct effect on system efficiency and durability. The epicyclic gear pairs have been explored from a load-sharing perspective under different conditions with different methods. In an ideal scenario, all the planetary load paths would carry the same load. However, there are many reasons for the unequal load distribution even when the planetary transmissions operate normally. Time-varying stiffness, manufacturing errors, assembly process errors
[5], and the phenomena that occur during operating conditions, e.g., tooth wearing
[6] and tooth gear wedging
[7], are unwanted phenomena that cause unequal load distributions. As a result, in addition to the predicted effects on dynamic behavior, there will be fluctuations in operating conditions, exceeding the design conditions and resulting in overloads
[5].
The number of planets in a planetary gearbox varies according to the design load of the system. Due to the existence of several planets, the planetary gear system’s (PGS’s) ability to withstand and transmit high levels of torque in a relatively small dimension draws the attention of many designers and researchers. The starting point for planetary load-sharing studies was a quasi-static approach
[8][9][10][11][12][13], and then investigations were developed concerning the dynamic behavior of the systems
[14][15][16][17][18][19][20][21][22][23]. Regarding these initial studies, there is a significant point that is carrying out the experimental tests in order to either validate their results or investigate the effect of some parameters on the dynamic behavior of the gear sets
[14][16][17][20][21][23]. Afterward, researchers attempted to consider more complicated models, with more details, in order to investigate the effects of diverse parameters on load-sharing. Li et al.
[24] investigated the effect of transmission error on load-sharing by using a two-stage planetary gear pair model and numerically solving the governing equation. Suzuki et al.
[25] published a study in 2011 to illustrate the influence of clearance between various components on an epicyclic gear system. They discovered that the carrier clearance should be less than the clearances of the ring and sun gear to provide proper load distribution. Compound PGSs have become increasingly prevalent in recent years due to their more compact capability. Fuchun et al.
[26] considered a compound planetary spur gear model and calculated the axial thrust force, which always exists due to the torsional pendulum torque acting on the planets.
The present paper outlines studies on single-stage planetary gear load-sharing and planetary gear phasing. Manufacturing, design, efficiency, tribology, and other research not directly relevant to load-sharing and phasing are excluded. Cooley and Parker published a first review article in 2014, summarizing studies on planetary gear dynamics and vibration in general
[27]. The present review paper provides an in-depth discussion of load-sharing and phasing in PGSs beginning with the first reported evidence of planetary gear usage and ending in 2022.
2. Load Sharing Model
In actual operating conditions, the external input load on planetary gears is not constant; consequently, the PGSs are examined by researchers under different conditions, such as the effect of gravity for huge PGSs or non-torque load for a diverse range of speed and mesh-pair characteristics. Non-torque load is introduced by the load components with five DOF, except for torque applied to transmit by a gear system. Indeed, all applied loads that do not lead to desired motion in the planetary gear system are called non-torque loads. They are unavoidable because of the rotor’s self-weight and external loads; an important example is the presence of inconsistent wind loads in a wind turbine drivetrain. The non-torque load might be applied in different directions; however, radial force and bending moment are major non-torque load elements affecting the load sharing of planetary gears
[28]. All non-torque loads should be absorbed by the main bearing on the main shaft, and only torque loads should be supplied to the gearbox. These loads are known to be conveyed to the gearbox and have an impact on the load-sharing. Non-torque loads and gravity force cause fundamental excitations in the rotating carrier frame, increasing gearbox loads and interfering with load-sharing. The effects of non-torque loads on the load-sharing of planet gears in a wind turbine gearbox were investigated by Park et al.
[28]. The radial force and the moment were the main non-torque load components that influenced the load-sharing of the planet gears, according to their findings. The influence of non-torque load on the load-sharing is dependent on the drivetrain system’s properties, such as its construction and gearbox size.
Gravity force becomes a substantial source of non-torque excitation as the size of the wind turbine rises. Gravity affects the planetary gear’s cyclic symmetry, resulting in unequal load distribution, according to the study by Qiu et al.
[29]. When the gravity is factored in, each component is subjected to non-cyclically symmetric gravity excitations. Consequently, the planetary gear’s cyclic symmetry is disrupted, and the planets’ motions are no longer consistent. The gear mesh force only excites the rotational modes in terms of vibration modes; nevertheless, the presence of gravity excites the translational modes. Guo et al.
[7][30][31] undertook many pieces of research to develop an analytical formulation for estimating the load-sharing and planetary loads of a wind turbine drivetrain when non-torque loads and gravity are taken into account. In 2020, Zhanwei et al.
[32] developed a model for wind turbine planetary gear set to consider the non-load torque in different directions under different operating conditions. The non-load amplifies the non-uniformity of load sharing between planets. Due to the combined effects of torque and time-varying non-torque loads, the frequency spectra of the meshing forces under the unsteady inflows include not only the rotation frequencies of the corresponding carriers but also the multiple frequencies of the carrier.
As aforementioned, it is common for the system to receive input torque or speed with some fluctuations; additionally, working in high-speed ranges or near resonances can result in significant differences in dynamic and static load-sharing, which cause design uncertainty. Experimentally, Götz et al.
[33] examined the dynamic load-sharing behavior of planetary gears from low to high speeds for various loads. They discovered that the vibration behavior of the drivetrain has a considerable impact on load-sharing behavior at high speeds and low loads. Higher load-sharing imbalances may arise from resonance zones. The load-sharing factors calculated under quasi-static conditions are relevant throughout a broad speed and torque range. Only at extremely high speeds should dynamic implications on load-sharing behavior be addressed. In addition, Ryali et al.
[34] conducted other experimental tests to demonstrate the impacts of additional parameters on load-sharing, such as input torque, planet mesh phasing, and gear tooth modifications. In the case of tooth profile modification, Xun and Dai
[35] showed that effective tooth profile modifications maintain dynamic load-sharing factors that are almost identical to those achieved under static settings. They also demonstrated that high input torque and flexible sun gear support assist in compensating manufacturing faults and enhance load distribution.
Xu et al.
[36] published their research showing that when the external input load is variable, the dynamic load-sharing factors of planet gears change as well, independently of the supporting stiffness. According to the simulation results, the larger the external input load, the better (uniform) the load-sharing across planet gears. In other words, raising the external input load and somewhat reducing the supporting stiffness of the planet’s flexible pins increases the probability of the planetary system’s unequal load-sharing. One of the design variables is the load-sharing between planetary gears, which has a significant impact on the performance and service life of a gearbox. Kim et al.
[37] proved that unequal load-sharing has an impact on the lifetime of a PGS. Regarding the load-sharing design factors, using a floating system rather than a non-floating system may extend the service life of a gearbox with planetary gears. Furthermore, smaller planetary pin diameter and greater planetary bearing clearance allow more efficient load-sharing between the planetary gears, increasing the system’s service life. The floating system was found to have a longer service life than the non-floating system; however, Rasekhi Nejad et al.
[38] demonstrated that the floating sun design generates more noise and vibrations than the fixed sun design.
Hu et al.
[39] examined the meshing impact characteristics of PGSs, including the meshing impact point, meshing impact time, and meshing impact force, and depicted the impacts on the load-sharing. They are dependent on time and types of errors. As a result, the gear transmission system’s characteristics are influenced by both load-sharing and dynamic load factors. The results show that considering the meshing impact effect of the planetary transmission system deteriorates the load-sharing and smoothness of the system. Considering the meshing impact, the system’s dynamic load factor fluctuates significantly, and the dynamic meshing force becomes chaotic. Sanchez-Espiga et al.
[40] studied the effect of different geometrical configurations, which modify the mesh phasing and planet spacing, on the load sharing and transmission error in a three-planet planetary gear set. They demonstrated at this point that the effect of spacing would be more remarkable if the gear supports were not rigid, but even with this consideration, the spacing affects the gear phasing. Geometry optimization is capable of decreasing the excitation and improving the load-sharing behavior.
The aforementioned chaotic behavior was confirmed in Ref.
[41]; in particular, it was found that complex dynamics take place when internal resonances are present in the gearbox; moreover, it was clarified that the dynamic imbalance could take place in perfectly balanced gearboxes; indeed, one of the well-known characteristics of the chaotic response is the symmetry breaking. Theling et al.
[42] presented a method for combining the structural optimization process with a tooth contact analysis for planetary gearboxes. Their method provided the ability to optimize the housing structure of the ring gear in terms of mass reduction while keeping the operational behavior in focus. As previously stated, the stiffness of the shafts, housings, and bearings, the number of planets, the quality of the gear wheels, and the working circumstances have an impact on the load-sharing of planetary gearboxes. The number of planets also has a considerable impact on the load distribution among planets. By increasing the number of planets in PGS, the sensitivity to the transmission error increases as well
[43]. Consequently, for two transmission systems with different numbers of planets by the same fault, the system with more planets shows higher unbalancing. It should be mentioned that this is true anytime that was talked about relative loads rather than total loads. In terms of the error impact on the load-sharing ratio, the input torque favors the gear set behavior. Thus, larger loads result in more balanced transmissions, regardless of the number of planets owing to the component flexibility. This is obvious even in arrangements where no consideration of wheel floatability has been made.
As far back as 1970, Seager
[44] attempted to describe the load distribution among planets in a simple PGS by conducting an approximate theoretical study of loading. One of the most important components of planetary gear pair research was developing a load-sharing model. Different characteristics, such as the number of planets, floating systems, and the flexibility of various sections, all had a role in this development’s progress. Bearing manufacturing errors, gear manufacturing errors (eccentricity error, gear thickness error, base pitch error), assembly errors, and meshing clearance variation induced by the simultaneous floating of all gears were taken into account in a mathematical model by Mo et al.
[45]. Their load-sharing approach was validated by experiments. An
N—planet helical planetary gear set, with six degrees of freedom (DOF) associated with each gear and the carrier, was studied in 2017 by Leque and Kahraman
[46]. As a method of recording the load and time dependence of gear meshes continuously, their model provided a distribution of gear mesh load. All types of manufacturing errors are included. They used their model to show the combined influence of errors on planet load-sharing to assist designers in the design of planetary gear sets.
In 2018, Hu et al.
[47] proposed a model for load sharing among planets, which was capable of dealing with planetary gear sets with any component level and gear set level design variations. In their research, they considered different parameters, such as different gear set kinematic configurations, gear modifications, and planetary gear sets with varying numbers of equally or unequally spaced planets. In 2019, they developed a planetary load distribution model to predict the overall transmission error of planetary gear sets with both planet pin position errors and gear run-out errors
[48]. They quantified the impact of carrier manufacturing errors resulting in unequal planet-to-planet load sharing on the gear set transmission error. A 3D dynamic load distribution model for planetary gear sets was presented by Ryali and Talbot
[49] in 2021 (based on the quasi-static formulation of Hu et al.
[47]). Next, they examined the dynamic behavior of planetary gear sets using the model they constructed to investigate the impacts of gear mesh phasing, tooth modifications, manufacturing errors, and contact ratios. In 2022, Pedrero et al.
[50] developed a method for calculating the load sharing between planets according to the meshing stiffness of each one at any given contact position.
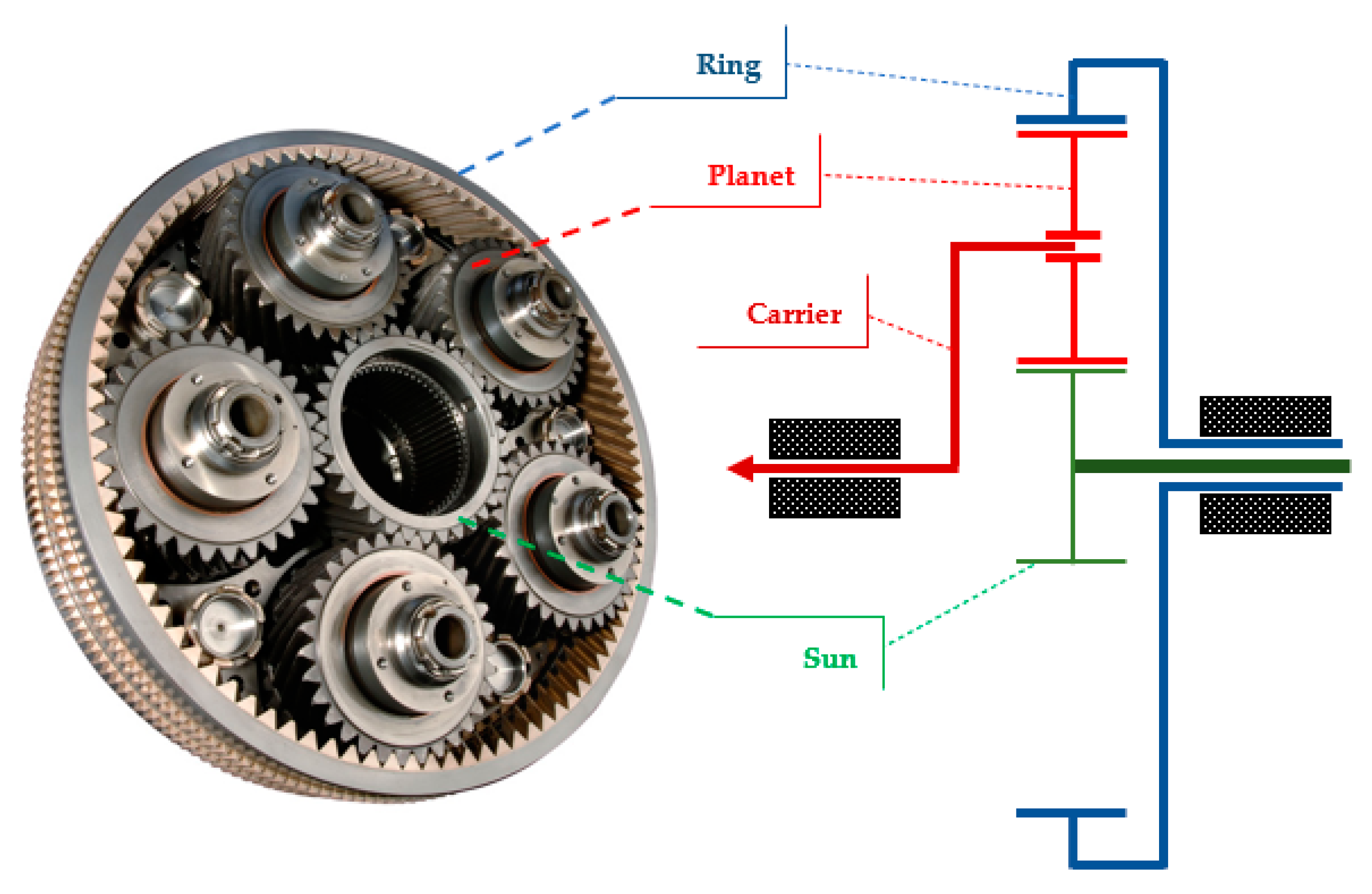
Figure 1 shows a planetary gear set with five planets. Each carrier, sun, or ring could be an output or input component. The carrier is the part that connects all of the planets together. The planet load-sharing has been defined in different forms based on the ratio of different parameters, e.g., force, torque, or even deformation. Iglesias et al.
[5] defined the load-sharing ratio (
LSR) as the ratio of the meshing torque in the sun due to each planet–sun meshes to the total input torque
Text defined a:
Figure 1. A planetary gear set with five planets.
This formula represents the relationship between the torque transmitted by the sun to each load path and the total external torque applied. Therefore, in a three-planet system, the perfect LSR would be 1/3.
Sanchez-Espiga et al.
[51] measured the load sharing by applying the different strain gauges to the root of the tooth. To calculate the
LSR from the deformation in the strain gauges, they defined the strain gauge load ratio (
SGLR).
SGLR refers to the relative peak-to-peak value measured from the strain gauge deformation due to the contact with any planet over the summation of all peak-to-peak values due to contact with every planet in a complete meshing cycle. The definition of
SGLR is defined as:
-
Not applicable to gear sets having a small module
-
Require strain gauges with high accuracy and sufficient sampling rate
-
Increase the probability of measurement error due to the high dependency on the deviations of actual gauge-mounting locations from the desired nominal location
-
Since errors in the planets, e.g., spacing, indexing, and run-out errors or eccentricities, could be time-dependent, the results might not be sufficiently accurate.
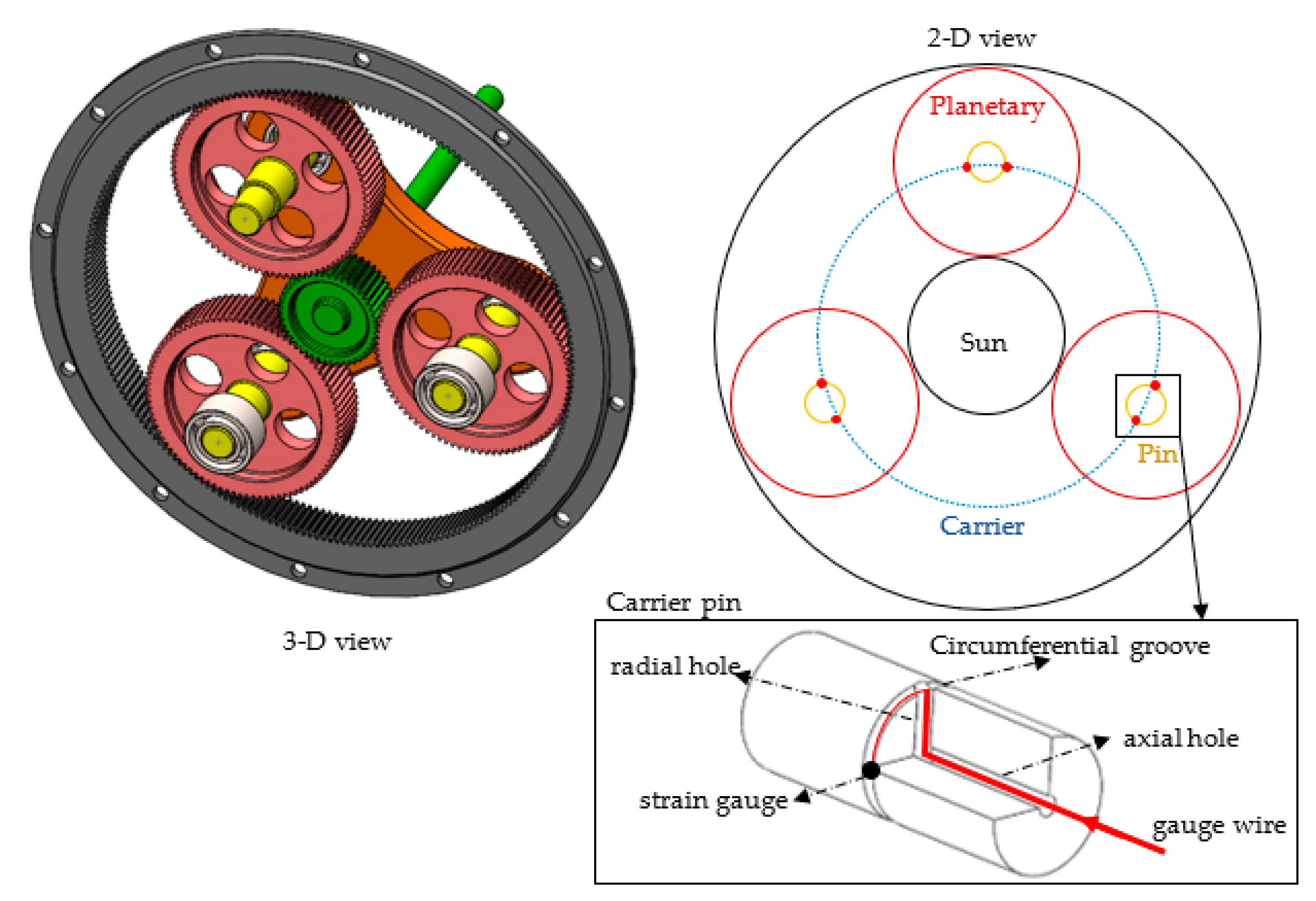
To overcome these negative points, Boguski et al.
[54] represented a new method to calculate the
LSR based on stress amplitudes. In their approach, each planet pin was strain gauged, as shown in
Figure 2, and it is required that the planetary gear set operates in a fixed carrier configuration such that the strain signals could be extracted without the use of a slip ring.
Figure 2. Pin instrumentation details and strain gauge locations.
Boguski et al.
[54] obtained the load-sharing factor
LSFn(t) of the
nth planet in a gear set as:
3. Effective Parameters on Load-Sharing
Although the exact equal load-sharing between all the planets cannot be expected in practice or even under quasi-static conditions
[15], researchers have put their efforts into improving the conditions that enormously affect the planet load-sharing. Investigating the influence of the different parameters on load-sharing, regardless of if it is positive or negative, is one of the interesting topics that has received intense concentration from scientists. It should be noted that these investigations have been carried out using different methods: experimental test
[13][55][56][57], a combination of numerical and analytical methods
[58][59][60]; and the FEM numerical method, which many researchers have been attempting to simulate the epicyclic systems by the latter method due to its accuracy, which shows a significant improvement during the last decades
[17][21][23]. Most experiments
[23][61][62] and finite element models
[60][61][63] are used for validation purposes. Studies could be categorized according to the kind of effect of these parameters:
-
Manufacturing errors
-
Elastic deformation
-
Bearing effects
-
Backlash
Planetary gears achieve their benefits only when the various planets bear almost equal loads. Engineers and researchers have paid close attention to the factors impacting planet load-sharing and the ways for improvement. When the load is averaged throughout a mesh cycle for ideal planetary gears with no faults, all planets bear the same load. Although producing an error-free gear system is almost impossible, operating circumstances are not always steady during the gear system’s lifetime, owing to load variation or maintenance situations. Therefore, undesirable faults such as tooth wear, misalignments, cracks, or tooth wedging may prematurely occur in gear systems when the load sharing is not uniform.
Fan et al.
[64] evaluated the load-sharing of planetary systems in the presence of misalignment. Their findings indicated that misalignment of a single planet pin has a detrimental impact on the load-sharing coefficient, with tangential misalignment having the highest effect. There is a relationship between load-sharing and tooth wear; load-sharing behavior influences the average amplitude of the meshing force, which impacts tooth wear, and vice versa; tooth wear accumulation increases the backlash that affects load-sharing behavior. Zhang et al.
[6] conducted a study in 2020 on the influence of tooth wear on load-sharing. They demonstrated that under ideal load-sharing conditions (no transmission error), the system’s instantaneous load-sharing performance degrades with the accumulation of contact fatigue wear on the tooth surface. However, when transmission error exists, the load-sharing performance improves slightly with the accumulation of contact fatigue wear on the tooth surface.
In 2019, Li et al.
[65] examined the effect of tooth cracks on load-sharing. They explored how compound planetary gear distributes loads in the presence of a crack in the sun tooth. They developed a lumped-parameter nonlinear model of the PGS and examined the influence of crack growth on load-sharing behaviors. When a crack begins, the damaged mesh pair’s load capacity reduces, resulting in an unequal load distribution among sun/ring–planet mesh pairs. As a consequence of crack expansion, load-sharing ratios rise nonlinearly and significantly. Han et al.
[62] examined the effect of the sun gear and ring gear cracks on the dynamic load-sharing factor in 2021. The result indicates that the ring gear crack has even less effect on the dynamic load-sharing between the external meshing gear pairs. During the shift from the ring gear to the sun gear, the intensity of the ring gear crack fault signal diminishes. They also examined the centrifugal force generated by the planet’s gear rotation. The findings indicated that when the planetary gear set is operated at high speed, the planet gear’s radial displacement may have a significant effect on the mesh characteristic; consequently, for this condition, lighter planet gear and increased supporting stiffness are required.
When manufacturing and assembly errors occur, the stresses on each planet might be markedly different, and this is unavoidable in reality. Errors in the location of the planetary gear’s pins are among the most critical and extensively studied. They can occur due to the manufacturing tolerances on the carrier pinholes. In the PGSs, manufacturing tolerances and the position of the planet pinholes on the carrier is responsible for errors in the positions of the planets. Such faults have been shown to have a significant impact on the system stability and the planet load-sharing. Having a center of rotation that does not match the geometric center of the gear is referred to as eccentricity error (also known as run-out error and imbalance), i.e., the deviation between the realistic and theoretical rotational center. Li et al.
[66] quantified the sensitivity of dynamic load-sharing on manufacturing errors and assembly defects. Their results show that eccentricity errors and assembly variations have an enormous impact on the dynamic load-sharing factor in comparison with tooth thickness variations and should be addressed by manufacturing gears and carriers to exact tolerances. Gu and Velex
[67][68] investigated the behavior of a PGS in the presence of planet pinhole and eccentricity errors. The findings demonstrate that, in contrast to conventional parallel-axis gears, planetary gear transmissions could be very sensitive to eccentricities, even when no central component is permitted to float. From a practical point of view, as long as the carrier is fixed, floating planets seem to be a viable option for distributing planet load. When it comes to rotating carriers, centrifugal forces at very high speeds are unfavorable because they decrease the overall sun-gear/planet contact ratios. For fixed ring-gear sets, some quasi-static aspects may be extended to dynamic load-sharing (equal loads on diametrically opposite planets). However, this symmetry is no longer seen with rotating carriers at high speeds.
An experiment by Liu et al.
[69] has shown that eccentricity errors affect the load-sharing of double-pinion PGSs. The load-sharing behavior is adversely affected by the planet eccentricity error, which is a combination of radial and tangential position errors. Radial position error has less influence on load-sharing behavior than tangential error, but its effects are bound to system configuration and cannot be ignored. An eccentric error has a more significant effect on the load-sharing characteristics than single faults or several errors, according to the research by Mo et al.
[70]. Sanchez-Espiga et al.
[43] investigated a model with errors, including pinhole location inaccuracy and tooth thickness deviation, under various mesh phasing conditions. They established that the influence of radial inaccuracies is not insignificant and must be considered. Additionally, its effect is more significant for sequentially phased transmissions than in-phase ones. However, the size of the radial error is far greater than that of the tangential error. Thus, production tolerances may be increased when radial pinhole position error is considered in contrast to tangential pinhole position error.
Other gear faults, including run-out and tooth spacing errors on individual gears, have been investigated in PGSs, but to a lesser extent than planet position matters. Rasekhi Nejad et al.
[38] published a paper in which they examined the influence of geometrical errors, planet gear eccentricity, and misalignment on the planetary gearbox performance of a wind turbine. Planetary load-sharing has been widely investigated under quasi-static situations. In this situation, the system deflections and reaction forces are estimated while vibration and inertia are ignored. Engineers often employ quasi-static analysis to understand, enhance, and solve planetary gear difficulties. Cao and Rao
[71], as well as Fan et al.
[64], investigated the influence of ring gear flexibility on load-sharing gears. For the low stiffness supports, the load-sharing coefficient reduces as the ring gear thickness increases. When the support stiffness is moderate and high, changing the thickness of the internal ring gear does not influence the planetary transmission system’s load-sharing coefficient.
3.1. Manufacturing Errors
Working under ideal conditions, which leads to a perfect load distribution among planets, is unrealistic, and the system commonly experiences some faults or errors, which makes planets carry out different loads
[9][10]. Manufacturing and assembly errors could be categorized into various types, and mainly they emanate from the lack of respect for tolerance controlling during the assembly or manufacturing process
[72]. The inaccuracy in the position of the gear, run-out error, and gear size (e.g., tooth thickness) are the three main manufacturing errors that are related to tolerance controlling and affect the load-sharing significantly. Manufacturing errors could be classified according to time and assembly process dependencies
[9]. Many researchers investigated these three parameters in order to determine the effect of each on the load-sharing in PGSs
[10][38][46]:
-
Time-invariant and assembly-independent errors: such as carrier and planet pinhole position errors and pinhole diameter errors.
-
Time-invariant and assembly-dependent errors: these errors, once the planetary gear set is assembled, maintain their value as the gears rotate, but the gear set can have different load-sharing outcomes depending on how each planet gear and planet pin are assembled in the carrier. Planet tooth thickness errors, planet bore diameter errors, planet bearing needle diameter errors, and planet pin diameter errors are some examples of these errors.
-
Time-varying and assembly-dependent errors: they have a time-varying effect on the load taken by each planet due to the way they are placed during the assembly of the gear set, since they are both rotation and assembly dependent, such as pitch line run-outs of the sun gear, planets, and the internal gear.
Bodas and Kahraman
[9] investigated the impact of different faults on planet load-sharing behaviors using a finite element model of a planetary gear set. Their analysis of an actual transmission gear set revealed that carrier faults from the first category (constant and assembly-independent errors) are the primary contributors to uneven planet load-sharing; as a result, position error and run-out error will be discussed in the following.
3.2. Position Error
The planetary gearboxes are capable of providing high-speed ratios and torque in a more compact package than fixed-axis gear systems. When a piece of equipment fails, it is critical to find out the problem and fix it. It is impossible to design new items unless the specific reason for failure has been determined. Planetary gearbox damage is caused by a multitude of factors. The most common issue among all kinds of errors or faults is position error; when all planets are working at their ideal position under unloaded conditions except one of them, the teeth of the planet with the error mate with the teeth of a ring/sun in an inappropriate time compared with other planets, which mean the mating surface for that planet with sun/ring comes closer or moves far away. Tangential errors are the parameters that make the planets engage early (or late) in the mesh cycle
[27]. Planet position error arises when manufacturing tolerances cause the planet shaft locations to deviate from their theoretical location.
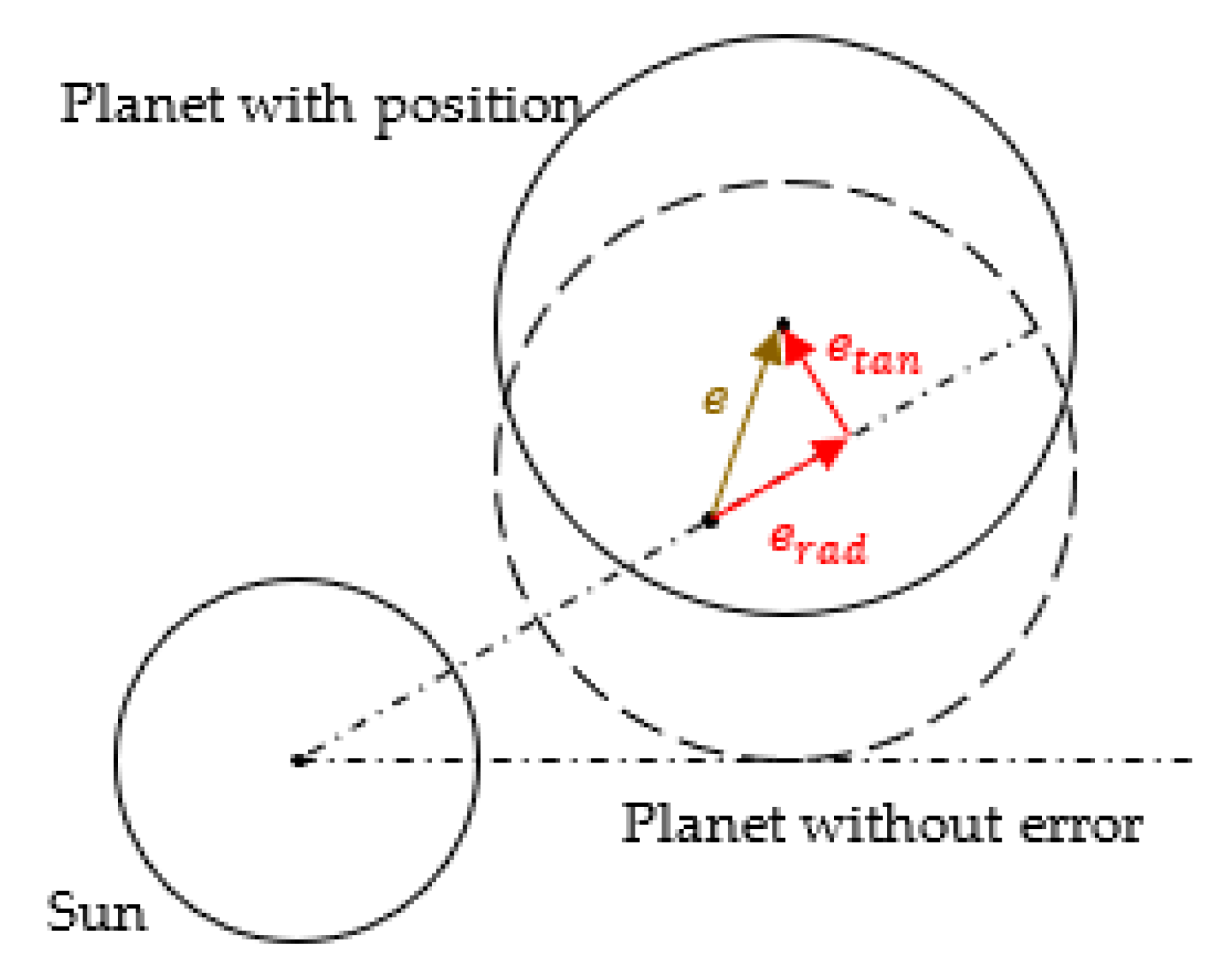
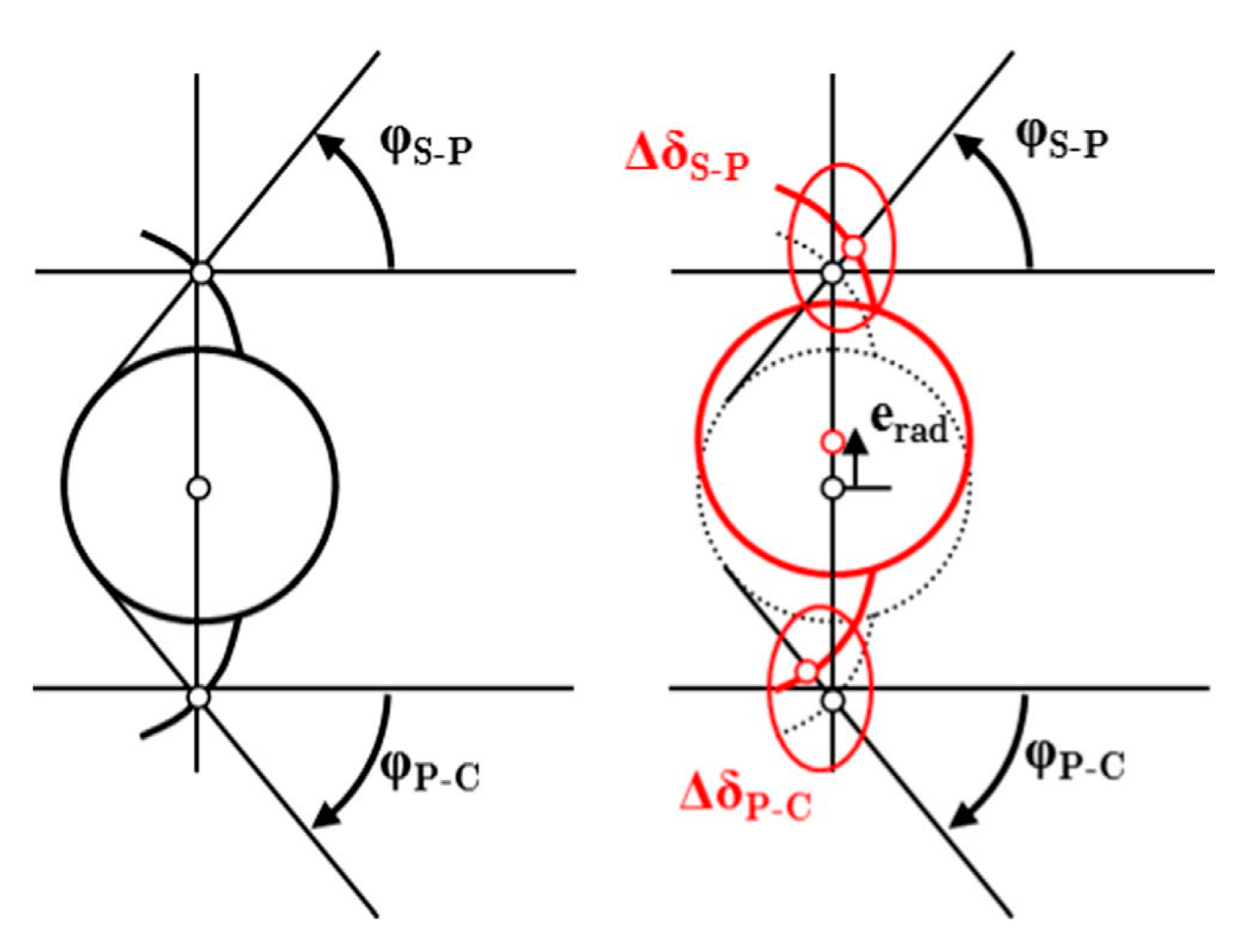
Due to the fact that the effect of this error is controlled by its direction, it is separated into two components, radial and tangential, as seen in Figure 3. The planet’s positioning error is split into two components: etan, parallel to the circumference at the planet’s center points, and erad, which represents deviations in the radial direction toward the system’s center. When the deviations are parallel to the direction depicted in Figure 3, the sign of the value is positive.
Figure 3. Planet position errors.
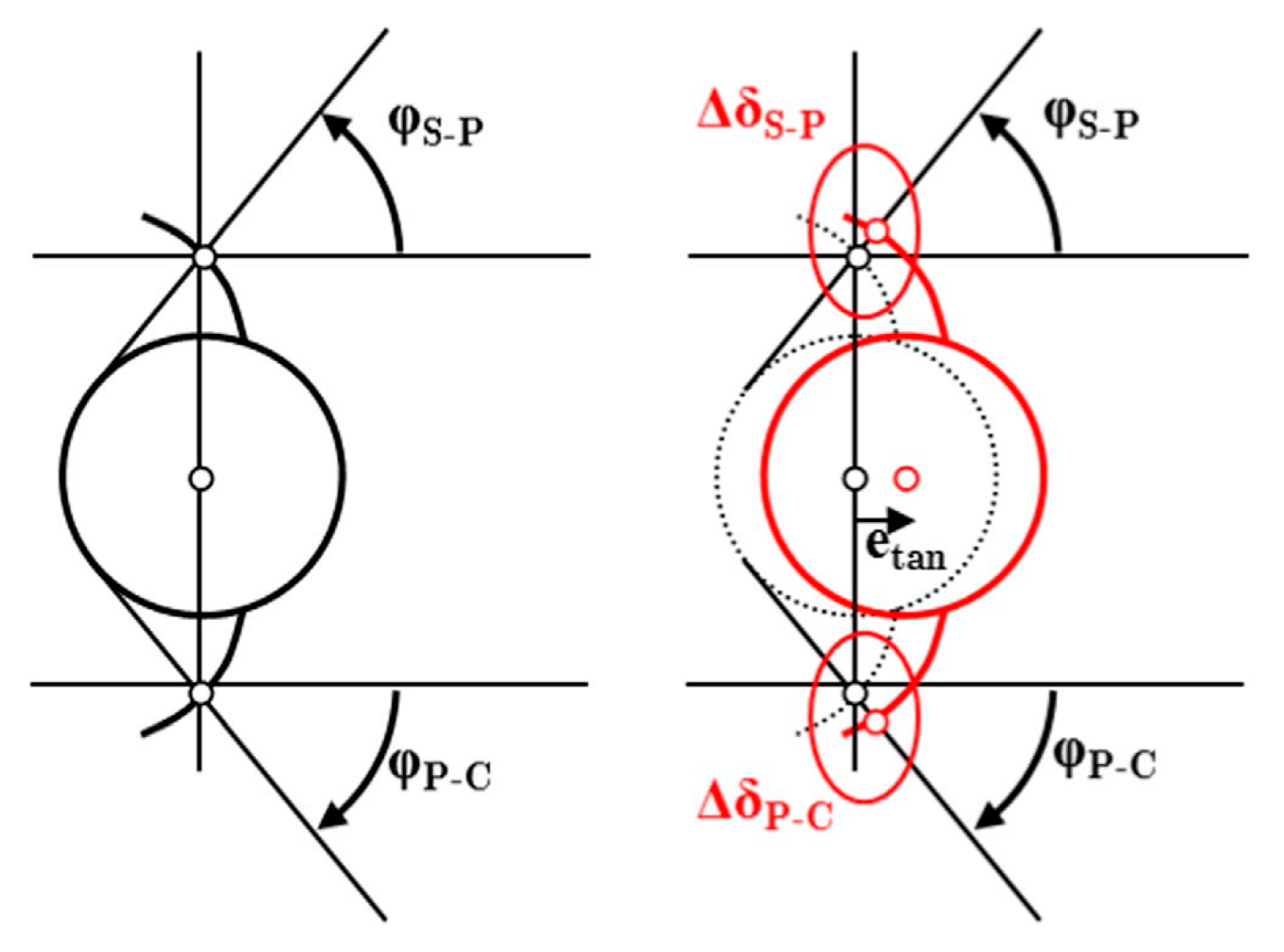
According to the direction of the error, the tangential component of the positioning error has the effect of advancing or delaying the starting of the contact of teeth of the planet with the error. As can be seen in Figure 4, there is a planet with a positive error etan. The change in the geometric overlap for the sun–planet (Δδp-s) and ring–planet (Δδp-r) meshes may be noticed when the planet center moves in relation to its theoretical location. The torque imparted via the sun–planet–ring path, with error, is influenced by these differences in the geometric overlaps, which results in a change in the related contact forces in both meshes. When the error is positive, and the torque is in the opposite direction, it causes a preload on the planet with the error.
Figure 4. Overlapping variation due to
etan [5], reprinted/adapted with permission from Ref.
[5]. 2022, Moslem Molaie.
The extra transmitted torque is far smaller while the radial positioning errors exist, as illustrated in Figure 5. Herein, the planet’s dislocation results in a reverse direction fluctuation in the overlapping geometric Δδ for each gear. Thus, the overlap variation is positive for the sun–planet mesh and negative for the planet–ring mesh. Knowing that the planet’s torque balance must be zero, it is evident that the planet will rotate away from the sun–planet contact, filling the gap created by the planet–ring contact. If the geometric overlaps are equal in absolute value, they compensate for each other, and the planet’s radial movement does not influence the transmitted load. It has to be considered that in certain PGSs, the pressure angle between the sun and planet is different from the pressure angle between the planet and ring. While it is true that the compensating overlap caused by the planet’s radial movement has a slight influence on the LSR (particularly when compared to tangential displacement), the LSR is far from ideal when pressure angles change.
Figure 5. Overlapping variation due to
erad [5], reprinted/adapted with permission from Ref.
[5]. 2022, Moslem Molaie.
A more significant effect on load distribution is due to the tangential position error than a radial error as a result of the changing mesh phasing among the planet gears
[36]. In non-floating arrangements, the tangential error has a significant effect on the load-sharing ratio. Under specific deviation and load conditions, it may even result in the full discharge of one or more gears. A negative tangential deviation (relative to the line of action) might result in the defective planet being unloaded. A positive deviation may result in the unloading of all non-defected paths
[5]. Thus, the consequences of positive deviations are far more severe than negative deviations. The tangential component’s influence on the load-sharing ratio affects the level of maximum contact force. Nonetheless, it was discovered that the relationship between the rise in contact forces and the variation of the LSR is nonlinear.
The radial component of the positioning error has substantially less influence on the LSR than the tangential component. Kim et al.
[57] conducted an experimental study on the effect of carrier pinhole position errors on planet gear load-sharing. When the planet pin was shifted in the radial direction (radial position error), the radial position error did not influence the system’s dynamic response. Furthermore, in contrast to the radial position error, when the planet with the tangential position errors is pushed ahead of the other planets, its bearing might bear the most force
[10][63]. Park et al.
[28] conducted a simulation to investigate the influence of pinhole position errors and various non-torque load components. Compared to non-torque loads, the pinhole position errors played a significant role in the load sharing of the planet gears. However, the influence completely depends on the characteristics of the drive train, such as the structure and size of the gearbox.
Additionally, when comparing a three-planet system to a four-planet system, the consequences of position errors were more pronounced in the four-planet case with different mesh phasing than in the three-planet case with the same mesh phasing. When the four-planet system was investigated with sun and ring position errors, the mean and peak-to-peak values of the bearing forces were more significant than when no errors were present. Along with oscillations caused by tooth mesh changes, the planet-bearing forces fluctuated as the planets rotated around the sun. The mean and peak-to-peak values of all planet’s bearing forces and load-sharing were equal. With three planets, the bearing forces fluctuated less than they did with four planets. In other words, the number of planets directly correlates with the sensitivity to position error; the more planets, the greater the sensitivity.
3.3. Run-Out Error
Run-out is a term that refers to the location errors that define the precision of the teeth on a gear and hence the accuracy of the transmission. Indeed, run-out is a concept that describes the inaccuracy of the tooth radial placement in relation to the pitch circle (see
Figure 6). It is the most considerable difference between all teeth’s nominal or theoretical radial positions and their actual or working measured positions. The run-out might result in structural integrity issues. Run-out creates an accumulation of pitch variation, which leads to non-uniform motion and transmission error. Run-out has a domino impact, affecting the majority of other gear quality metrics, such as involute and/or tooth shape, index and/or pitch error, lead deviation, and noise and vibration
[5][63][73].
Figure 6. An exaggerated schematic of run-out error
[74].
While the system experienced a run-out error, the bearing forces reported much greater than normal working conditions, see Ref.
[10]. The planet-bearing forces had the same peak and mean values as the carrier-bearing forces but exhibited different phasing and extra variations due to carrier rotation. Except for oscillations caused by carrier rotation, the magnitudes and forms of the bearing forces were comparable to those measured when the sun position was incorrect. The main patterns seen in the case of three planets were similar to those observed in the case of four planets. Except for the oscillations caused by carrier rotation, which occurred once per carrier rotation, the magnitudes and patterns of bearing forces and load-sharing were almost identical in the case of the ring and the sun gears run-out errors.
3.4. Influence of Bearing and Backlash
Bearings are fundamental parts of the transmission system, which could have an eminent effect on manufacturing error due to their widely variable stiffness for all three types of gears: sun, planets, and ring
[72]. As Guo et al.
[7][30] showed in 2010, clearance inside carrier bearings significantly affects bearing stiffness. The increment in the pitching moment, transferred from the rotor to the gear meshes, leads to disturbing the planetary load-sharing and causes edge loading. Edge loading increases the likelihood of tooth pitting and planet-bearing fatigue, leading to a reduction in gearbox life. Through carrier bearing clearance, the shaft pitching moment was passed to the gear meshes and planet bearings. In this condition, the planet bearings are at risk of sliding, and the gear teeth are at risk of contact loss, both of which lead to the gearbox’s lifetime reduction.
Guo et al.
[7][30] demonstrated the influence of bearing clearance on tooth wedging, which disturbs planetary load-sharing and lowers planet-bearing life. Tooth wedging in planetary gears causes uneven load-sharing and increases the maximum planet-bearing loads by disrupting planet gear symmetry. Consequently, it might result in bearing failure and tooth damage. Tooth wedging could be avoided if the carrier-bearing clearance is smaller than the tooth backlash. If the sun support’s stiffness equals or is more than the ring stiffness, tooth wedging might occur even when the bearing clearance is less than the backlash. Sheng et al. in 2015
[75] and Zhang et al. in 2016
[76] studied the effect of bearing and backlash in PGSs. They demonstrated that with proper bearing clearance and backlash, load-sharing performance might be improved as long as resonance areas are avoided. Their findings reveal that, in comparison to bearing clearance, the backlash has the greatest effect on load-sharing behavior. Increasing the backlash increased the load-sharing factor remarkably, resulting in the appearance of a positive gear impact.
The backlash of the gear should be appropriately controlled throughout the design process to ensure the whole system performs properly
[77]. In 2020, Zhang et al.
[78] investigated a different bearing, the journal bearing, on load-sharing. They demonstrated that raising the rotation speed reduced the eccentricity of the journal bearing and enhanced the system’s load-sharing performance. The eccentricity of the planet rose as the torque increased; however, the change in the tangential component was reduced. Indeed, the load-sharing performance deteriorated at first, then improved, and there was a turning point. Guo et al.
[79] studied the same problem as Zhang et al.
[78], investigating the effect of journal bearings on load-sharing; they explored the influence of the main characteristics such as lengths and diameter ratios, relative clearance, and the effects of operating conditions, e.g., viscosity, load, and rotation speed. The load-sharing factor decreased as the journal bearing clearance or load increased. With a modification of the length and the diameter ratio, Guo et al.
[79] achieved a minimum load-sharing factor. The load-sharing factor rose as the viscosity increased at the same rotational speed and load magnitude.
4. Enhance the Load-Sharing
One of the main subjects, which has been attracting remarkable attention from researchers, is to find a method able to improve the torque distribution or load-sharing among planets. The flexibility and rim thickness of the internal ring plays a significant role in load-sharing, noise, and durability of PGSs. To illustrate this point, for a normal automotive transmission gear set, a 1 mm reduction in rim thickness could lead to a decrease in ring gear mass of around 20%. Not only does it increase the flexibility and reduce the stress on other gears, but also this reduction alleviates the effect of some errors and piloting inaccuracies, although it should be limited
[8][15][16][58][80]. Hayashi et al.
[19] performed an experimental study to demonstrate that load-sharing improves with an increment of the transmitted torque.
Mostly unequal load-sharing is inevitable in the traditional PGS where the center distances between gears are fixed; consequently, the stress distribution at each mesh point is variable. A wide range of parameters can affect load-sharing and stress distribution, such as manufacturing tolerance, accuracy, and component deflection. For the sake of manufacturing errors or working conditions in a rigid system, it might happen that one planet comes in contact with the ring or sun before the other planets. In general, to compensate for the destructive effect of errors in the system, there are some approaches that are suggested and considered as the main goal of researchers’ studies:
Undeniably, each of these models has its advantages and disadvantages; for instance, flexible ring gears do not lead to a significant output, as the ring gear’s radial deflections are insufficient to compensate for clearance (backlash) changes at the different mesh positions
[81]. Moreover, other methods are employed in order to obtain an enhancement in load-sharing among planets, such as profile modification
[82][83] and flexibility of the system structure
[78]. Methods for optimizing the reliefs have been published in the recent past
[84][85]; however, such methods have been mainly focused on gear pairs. The profile modifications remove edge contact, a major source of uneven load-sharing in PGSs with a floating center component. The force is significantly reduced when the relief is performed. This drop is mostly due to an increase in the load-sharing ratio
[83]. Further, Zhang et al.
[78] showed that enhancing the system’s structural flexibility improves the load-sharing performance. In comparison to the pin shaft, the ring gear’s flexibility has a significant influence on the gear system’s load-sharing performance. Moreover, the American Gear Manufacturers Association (AGMA)
[86] listed 19 different methods to improve load sharing among planets in a planetary gearbox:
-
Higher quality gear members.
-
Increased precision of carrier elements that locate planet gears.
-
Matching planet gear sets by tooth thickness.
-
Improve tooth alignment of compound planets by using matched sets of planets (compound epicyclic only).
-
Oil film thickness variation due to changes in oil flow and loads in journal bearings.
-
Allowing radial float of one or more elements.
-
Elastic deformation of the ring or the sun gear, or both.
-
Reducing tooth stiffness.
-
Elastic deformation of planet gear shafts.
-
Elastic deformation of planet carrier.
-
Eccentric planet shafts with load responsive rotation device.
-
Load sensitive displacement of journal bearing oil films.
-
Load sensitive consumption of planet shaft material when utilized as a journal bearing.
-
Improved gear and shaft alignment.
-
Reduced shaft run-out.
-
Improved bearing quality and alignment (true position of bearing location in carrier).
-
Improved assembly (location) of the carrier if the carrier is split axially.
-
Improved compliance of components (gears, shafts, bearings, housing).
-
Improved dynamics (operating speed versus resonant frequencies).
4.1. Floating Systems
This section summarizes the findings of the researchers’ investigation into two major parameters that they thought to be intriguing. The floating system and the flexible pin are two approaches that have been employed to enhance the distribution of load. Because at least one of the coaxial members (the sun, ring, and carrier) is free to move radially in floating systems, it is conceivable for the coaxial members to move with respect to each other. In the literature, it is well acknowledged that floating one or more of these components results in markedly enhanced load-sharing characteristics. The main benefit of floating systems over non-floating systems is that the system with the float components compensates for a part of the position error. The rest of the errors are neutralized by system deflections, which causes the load-sharing imbalance
[63]. The flex-pins enable the planets to move, ensuring their alignment is exact. As a consequence, it decreases stresses on the gears; therefore, it is possible to create more reliable PGSs. This method has been successfully used for a wide variety of industrial and aerospace gears operating at high levels of speeds and torque
[81].
The common method, which could be surprisingly effective in enhancing the load-sharing situation, is that the carrier or sun is allowed to float in epicyclic systems
[17][21][22][23]. In the floating system, the center of at least one of the coaxial components (the sun, ring, or carrier) is free to move radially. It is widely accepted that floating one or more gears significantly enhances load-sharing characteristics. The main advantage of floating systems over fixed systems is that system float compensates for certain positional inaccuracies such as run-out, non-uniform diameters, and teeth spacing may be corrected for, resulting in improved stress distribution among the planets
[63]. The interesting point is that a floating member could compensate for unavoidable errors
[2], and floating radially either the carrier or sun has the same effect on load-sharing and reducing tooth stress; however, it is not recommended to provide both floats in PGSs as it induces tooth stress
[8][14][72][87][88]. Numerous studies have been conducted to quantify and estimate planet load-sharing as a function of gear set errors.
Seager
[44] provided a simple model demonstrating the necessity of floating sun gear in PGSs with three to six planets. Kahraman
[22] provided a dynamic model of a planetary gear set that includes gear eccentricities and carrier pinhole position errors. Their results showed that planet load-sharing is essentially a quasi-static phenomenon that does not need the inclusion of dynamic factors. Boguski et al.
[54] introduced a novel approach for measuring load-sharing under quasi-static situations in 2012 that eliminates most of the previous model’s weaknesses. They created a test setup for PGSs operating under radially floating sun gear circumstances. Chung et al.
[89] proposed some simulations to investigate the effects of floating members on the load-sharing characteristics and the strength of a planetary gear set with non-torque load and carrier pinhole position error.
Developing a new method for evaluating planet load-sharing based on strain gauges applied on planet pins enabled continuous and immediate evaluation of planet loads regardless of whether the errors were constant or time-varying. It was shown that a four-planet gear set could transfer loads evenly between two diametrically opposed planets, but the problem of unequal load-sharing between two nearby planets remains. In 2018, Xu et al.
[36] investigated the dynamic load-sharing characteristics of a PGS operating at a high load. They included a multiple floating PGS with a floating central component and a flexible quasi-floating planet supporting pin. Their results indicate that when both the sun gear and planet gears are multi-floating together, the system performs effectively in terms of load-sharing.
When planet gear position errors are constant, reducing the flexible pin stiffness of the planet gear or increasing the external input load may greatly improve load-sharing. Only by gradually decreasing the supporting rigidity of the sun gear and carrier could it be possible to decrease the dynamic load-sharing factor gradually. Instead of diminishing the sun or carrier supporting stiffness, dynamic load-sharing could be increased by reducing the stiffness of the flexible pins.
4.2. Flexible Pin
Although floating sun-gears are popular, it has been shown that the flexibility of the planet shafts can have a significant impact on load-sharing
[22][90][91]. Ray Hicks, a British engineer who began working with gears in 1954, created the flexible pin nearly 70 years ago. Compact Orbital Gears was established in 1964 by Ray
[92], who invented his unique epicyclic gear system that employed compound cantilever flexible planet shafts known as flexible pins. It is based on the principle of distributing loads evenly among planets through a torsional flexible connection to a planetary carrier. Rather than specifying the angular positions of the planet gears, the flexible pins were intended to deflect freely in a circumferential direction; therefore, it leads to force balance distribution among the planets for transmitting torque at different levels
[81].
Figure 7 compares the behavior of traditional (
Figure 7a) and flexible-pin (
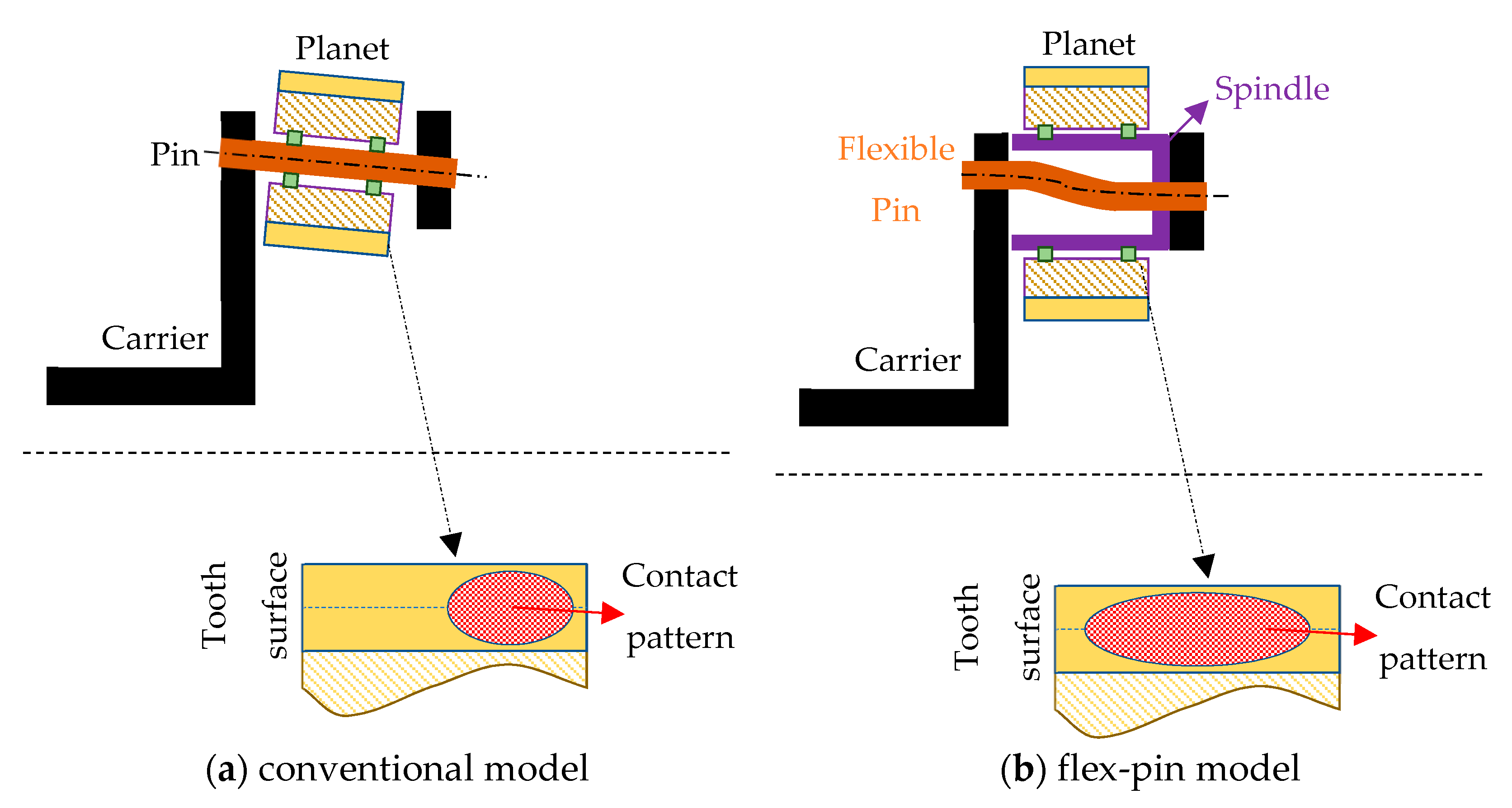
Figure 7b) PGSs during a shock load. When the structure of the traditional solution is subjected to higher-than-nominal stresses, it deforms, causing planets to tilt from their optimum positions. It leads to unequal planet-bearing loading and worsening the gear mesh contact pattern
[93]. Increasing material stiffness through more material is typically the best way to prevent such occurrences, although movement cannot be entirely halted. On the other hand, the planet is free to move in a regulated manner while remaining parallel with the flexible pin solution. In 1967, Hicks
[92] showed a method to improve load-sharing between planets, which involves a double cantilever pin and sleeve arrangement when used with a cantilever-type carrier. This method was used in the industry and was discussed in industrial technical papers. The major objectives of the invention were to lower the required machining precision, i.e., raise the permissible tolerances, while increasing load distribution uniformity on each of the planet wheels of the epicyclic gearing; the invention was or might be applied to other types of gear systems.
Figure 7. A comparison of conventional and flexible-pin PGSs. (a) conventional model (b) flex-pin model.
The epicyclic gear system of Hicks’ concept was made up of a single flange carrier and flexible pins fixed in and projecting from the flange. The carrier pins project from the single carrier flange into the planet gears in this configuration, offset axially from the planet gears. To support the planet, each carrier pin has one end fixed in the carrier flange and the other end placed into a sleeve that returns over the pin but is separated radially from the pin. To address this issue, Fox and Jallat
[94] modified Hicks’ ideas by cutting a notch with fillets into a symmetrical flexible pin in 2007.
Montestruc et al.
[90] showed that a large number of planets could be made accessible by the use of flexible planet pins. Additionally, they demonstrated that the use of flexible pins and other forms of flexible mounts improves load-sharing even at greater tolerance levels. As a result, flexible mounts with lower precision grade gears are suitable. As previously shown, load-sharing is substantially related to torque, and the load-share fraction of the most heavily loaded planet is not constant and should be revised for each load case during fatigue life prediction. Otherwise, severe errors in the estimate of fatigue life are probable. Additionally, it is shown that flexible pins with a small spring stiffness diminish the magnitude of vibration forces generated by spur gears moving between one and two tooth contacts, regardless of the number of planets utilized. Flexible pins reduce the necessity for straddle mounting, allowing the greatest number of planets to be employed, which leads to an increase in the input torque density in any epicyclic ratio of power transmission systems. Pin stiffness and position tolerances are critical characteristics in this kind of design since they have a significant effect on dynamic performances.
Zhu et al.
[95] demonstrated the impact of the pin stiffness and position errors on the natural modes and dynamic response of a system. The effects of the pin stiffness on the deviation of tooth contact forces in the sun–planet and ring–planet gear pairs are examined in order to achieve a better understanding of the link between mesh characteristics and input speed fluctuations. The computed supporting forces of the planet gear are analyzed to better understand the load-sharing characteristics of the power transmission system owing to pin errors, pin stiffness, and input load. They demonstrated that pin stiffness has a considerable effect on natural frequencies. As predicted, when pin stiffness increases, the number of natural frequencies in the lower frequency range decreases; however, pin error has a negligible influence. They demonstrated that low pin stiffness, small pin tolerance, and higher loads are desirable for load-sharing. Additionally, by modifying pin stiffness, load-sharing could be improved even when pin tolerance values were considerable. It could be suggested that flexible pins compensate for gears with a lower precision grade. Yoo et al.
[96] modified the planetary gear set for a wind turbine gearbox in order to raise the power density and decrease the load on the planet gears. To improve the LSR, they designed a flexible pin to apply in a single helical-geared PGS, which was previously considered impractical.
5. Planetary Gear Phasing
For a planetary gear system, when the teeth number of the planet, ring, or sun is not proportional to the number of planets, the planets are out of phase. For the case of in-phase planets, all planets mesh with the sun and the ring at the analogous points; in this situation, the number of teeth of the sun gear, planet gears, and the ring gear is multiple of the number of planet gears
[97]. Parker
[98] investigated the analytical basis for planet phasing in spur planetary systems and extended the concept to systems with unequal planet spacing. The effectiveness of planet phasing to suppress planetary gear vibration in certain harmonics of the mesh frequency is examined based on the physical forces acting on the sun planet and ring planet meshes. The results are developed in terms of the physical mesh forces and are not tied to any lumped-parameter models. For planet spacing conditions, potential resonances in at least half of the mesh frequency harmonics are suppressed without attempting to optimize the phasing. Planet phasing cannot suppress all potential resonances. Later, in 2003, Parker et al.
[99] set out a complete analytical description of each mesh phase relationship. They showed that mesh phasing has a considerable impact on the static and dynamic behavior of planetary and epicyclical gears. It was provided the necessary relationships to satisfactorily incorporate mesh phasing in analytical models. Attention was focused on the relative phase differences of the mesh tooth variations, and these relative phase differences are exactly the same as for the mesh stiffness variation functions.
In 2016, Shweiki et al.
[100] proposed the finite element method with multibody simulation to investigate mesh phasing and analyze the dynamics of a planetary gear in a wind turbine transmission model. In this method, nonlinear static finite element simulation is used to generate a static transmission error curve, and multibody analyses are performed on a three-dimensional model of the transmission. Two phasing strategies have been analyzed, with in-phase and sequentially phased planets, to minimize unwanted vibrations and improve system dynamics.
In 2007, Parker and Ambarisha
[101] used a two-dimensional lumped-parameter model and a finite element model to analyze the nonlinear dynamic behavior of spur planetary gears. These models are compared qualitatively and quantitatively; moreover, mesh stiffness variation excitation, corner contact, and gear tooth contact loss are considered in their analyses. When nonlinearity from tooth contact loss occurs, rotational and translational vibrations in planetary gears are suppressed by mesh phasing rules. Huang et al. provide an investigation of the influence of the system-inherent phase on the relationship between two sides of the tooth profile during the meshing process. Their method considered high-frequency impact intervals in two-parameter conditions combined with a particular Poincaré mapping. Furthermore, a mathematical model of an asymmetric multi-state mesh of a spur gear pair was established. The results indicate that the asymmetry phenomenon in different meshing states significantly affects the nonlinear characteristics of the back-side impact system. It helps select the conditions to avoid a stable high-frequency impact
[102].
Parker et al. studied an analytical solution for investigating the dynamics of lumped-parameter planetary gears with time-varying mesh stiffness excitation and teeth separation nonlinearity. It was analyzed amplitude–frequency relationships for nonlinear resonances of all modes, including distinct rotational, degenerate translational, and degenerate planet modes. They presented a simple rule that governs the occurrence of potential parametric instabilities for a given mesh phase. The problem of multiple coupled modal amplitudes for a degenerate mode resonance reduces to one single unknown modal amplitude using mesh phasing results and modal properties. Numerical integration of a planetary gear model verifies all the analytical results. These numerical results also show that parametric instabilities can conduce to nonlinear behaviors, such as jump phenomena, period-doubling, and quasi-periodicity
[103].
Ryali et al.
[49], in 2021, studied the influence of several components such as gear mesh phasing, tooth modifications, manufacturing errors, and contact ratio on a three-dimensional dynamic load distribution model of planetary gear sets under various gear mesh phasing conditions. Herein, the multibody dynamics problem is solved by a numerical integration scheme combined with an iterative elastic contact algorithm. The introduced model records the unique harmonic content of the gear mesh in dynamic response resulting from the mesh phasing and errors in the gear set. Overall transmission error captures only the in-phase mode resonances, while central member transverse motion captures all sequential-phase mode resonances. In 2021, Viadro et al.
[53] presented a numerical approach for the calculation of the load sharing in planetary transmissions. They simulated the load sharing for different scenarios, including in-phase and sequentially phased transmissions. They concluded that the mesh phasing, the synchronization between the strain gauge acquisitions, and the imbalance-creating factor had a crucial impact. The discrepancies between the real load sharing and the measured data were shown in the results from the geometrical point of view.
5.1. Efficiency Effects
A tribo-dynamic analysis for planetary gear sets of hybrid-electric-vehicle configurations was presented by Mohammadpour et al. in 2016
[104]. They figured out the lubricant film thickness, friction, and efficiency of the meshing gear teeth contacts. In their research, no phase difference was considered at different meshing points between the gear sets. Later, in 2018, Fatourehchi et al.
[105] analyzed the planetary wheel hub gears of off-highway vehicles. In this research, a combined tribo-dynamic model of planetary wheel hub gearing system is presented for heavy and off-highway vehicles. The dynamic model possesses six torsional degrees of freedom, including the sun, three planets, ring, and carrier, coupled with an analytical lubricated contact model of meshing teeth pairs. The results show that noise, vibration and harshness refinement and transmission efficiency can be obtained with mesh phasing of the system planetary branches under near-optimal conditions. This research also presented the inexorable interplay of transmission efficiency and noise, vibration, and harshness refinement.
5.2. Experimental Investigations
The experimental study carried out by Gawande et al.
[106] analyzed the effect of planet phasing on noise and subsequent resulting vibrations. Gear meshing in the planetary gear set, which is the mechanism for changing the ratio of an automatic transmission, produces gear noise in a wide range of driving conditions from low to high speeds. Herein, it is observed that the internal excitation caused by the variation in tooth mesh stiffness is a crucial factor in producing vibrations. The planet phasing arrangement reduced the noise level and resulting vibrations. The results show that planetary gear set noise and vibrations can be reduced by applying the meshing phase difference.
Recently, Chen et al.
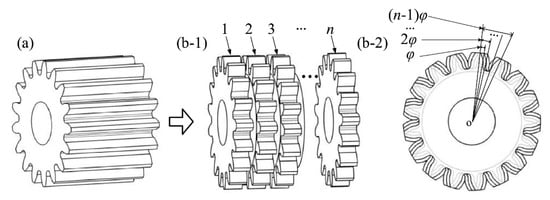
[107] proposed novel high-order parallel spur phasing gears to reduce the fluctuation of mesh stiffness; in this method, transmission error and vibration displacement are verified by means of theoretical and experimental results. The gear engagement between a pair of spur gears has a mesh phase difference when a spur gear is divided into two axially connected layers with equal tooth width and with different circumferential positions,
φ, (staggered phase angle), see
Figure 8b. A high-order phasing is defined as a gear that includes
n layers with equal tooth widths along the axis and equal
φ (
Figure 9). The mesh stiffness of the high-order phasing gear pair is derived on the basis of the time-varying mesh stiffness of the spur gear pair. The optimal staggered phase angle and other parameters of high-order phasing gear sets are optimized experimentally with the aim of achieving near-zero fluctuation in mesh stiffness. The results concluded from the experiments show that the optimum suggested phase angle of the two-order phase gear is
φ = π/
z under all experimental conditions. The optimal condition established the minimum peak-to-peak value of transmission error and vibration displacement
[107].
Figure 8. The phasing gear and staggered phase angle
[107], reprinted/adapted with permission from Ref.
[107]. 2022, Moslem Molaie.
Figure 9. Schematic diagram of
n-order phasing gear
[107], reprinted/adapted with permission from Ref.
[107]. 2022, Moslem Molaie.
5.3. Frequency Interplay
Parker et al.
[108], in 2006, analytically investigated how mesh phasing can suppress planet mode response in planetary gears having equally spaced planets or diametrically opposed planet pairs. Mesh phasing rules established by using the symmetry of planetary gears and the gear tooth mesh periodicity are gathered for rotational systems. Guo et al.
[109] investigated the effectiveness of adopting mesh phasing on a classical coupled lateral-torsional lumped-mass model of split-path transmissions comprising spur gears with dual power paths. A novel method for eliminating the rigid-body displacement of a time-variant system is proposed. In their model, each gear has three planar degrees of freedom, and also time-varying mesh stiffnesses are considered (
Figure 10). They also ignored all manufacturing and assembly errors. The modal equations are solved by the Runge–Kutta direct numerical integration method (‘ode45’ function in MATLAB). They showed that some modal responses of split-path transmissions and vibrations in some directions can be suppressed by mesh phasing.
Figure 10. Dynamic model of SPT
[109], reprinted/adapted with permission from Ref.
[109]. 2022, Giovanni Iarriccio.
5.4. Instability
In 2002, Parker et al.
[110] investigated parametric instability for planetary gears. The time-varying mesh stiffnesses were modeled as a rectangular waveform with different contact ratios and mesh phasing. They adjusted the contact ratios and mesh phasing and also suppressed particular instabilities. The strong impact of parametric instability on the response was shown by numerical simulation of tooth separation. Later, in 2008, Parker
[111] investigated how the ring planet mesh phasing and contact ratio affect the parametric instabilities of a planetary gear. He used the parametric excitation of a rotating ring, which was extracted in his previous investigations. Noise and vibration due to parametric instabilities were suppressed by certain ring–planet mesh phasing and contact ratio conditions. In the same year, Parker and Wu investigated the parametric instability of planetary gears using a hybrid continuous-discrete model by assuming an elastic continuum ring and considering the lumped subsystem sun–carrier–planets
[112]. The ring gear was modeled using the thin elastic body assumption, and its bearings and supports were represented by a uniform elastic foundation with radial and tangential stiffnesses
[113]. In the case of equal planet spacing and depending on the multiplicity of the unstable modes, three different instabilities have been defined: distinct-distinct, distinct-degenerate, degenerate-degenerate. Using the multiple scales method, closed-form solutions for the instability boundaries have been obtained for both in-phase and sequentially phased mesh conditions. Further improvements to the aforementioned model are given in Ref.
[114], where Coriolis and centripetal accelerations have been taken into account. Recently, Ericson and Parker
[115] have shown the importance of considering elastic body deformations in theoretical models. In particular, elastic-body vibrational modes involving the ring gear have been experimentally observed. Since they result in significant dynamic mesh stiffness fluctuations, i.e., large tooth deformations, modal interactions could make the system prone to parametric instabilities.
6. Fault Effects on Planet Phasing
Some researchers investigated the dynamics of planetary gears when some kind of fault occurs in different parts of the planetary gear systems. Feng et al.
[116], in 2017, used phase angle data for fault detection under non-stationary operational conditions to reduce the complexity of signal and ensure the diagnostic capabilities of a planetary gearbox system. Herein, the cosine phase angle was originally proposed for fault detection of the rotating machines. The degree of complexity of the data is reduced by considering the complex amplitude modulation nature of the measured vibrations. The proposed angle-based signal contains characteristic fault information and is ready to be used for condition monitoring of the planetary gear system. Under different operational conditions, the advantage of the proposed angle-based signal is to recognize faults, which are intractable by the primary measured vibrations.
In 2019, Peng et al.
[117] used mesh phasing for distinguishing between faults on different planet gears and used localized seeded spalls in tests to give impulsive signals. It is observed that the vibration signals recorded on a planetary gearbox test rig exhibit different characteristics depending on the position of the faulty gear. A phase-based approach is offered to differentiate and locate the faulty planet gear position using vibration response signals and developing an indicator. The position of the faulty gear was found effectively. Sanches-Espiga et al.
[43] considered mesh phasing with various errors, such as tooth thickness and pinhole position errors, in their study on three-planet and five-planet planetary gears in 2020. It caused an imbalance in the load-sharing ratio. These errors for sequentially phased transmissions were more effective than the case of in-phase transmissions.
Liu et al. presented a flexible-rigid coupling dynamic planetary gear model with a rectangular local planet-bearing fault. In their model, the flexible ring gear and flexible supports of the ring gear and sun gear were formulated. It was analyzed the time-varying impulse force caused by the fault, effects of the fault width, moment, and input speed on the vibrations of planetary gear, and presented some advice for fault detection methods of planet bearings
[118].
Luo et al.
[119] developed an improved phenomenological model for studying the broken tooth of the sun gear under different fault sizes. Herein, two types of impacts were considered: contain meshing impacts and fault impacts; moreover, nine assisted phases were proposed based on the time difference between these impacts to analyze the model’s correctness. As a result, it is shown that these phases may correspond to two fault sizes when performing fault diagnosis and the stiffness characteristics of the faulty gear pair settled this problem.
In 2022, Ha et al.
[120] proposed a novel D-norm-based time synchronous averaging method for the fault diagnosis of a planetary gearbox without the use of an encoder system. D-norms are amplifications for fault-related impulse noises. Moreover, D-norms enable time synchronous averaging by alleviating the slight phase error without an encoder to reduce noise. It was found that for the case studies involving an analytic simulation and a 2-kW planetary gearbox test-bed, the proposed method outperforms the conventional minimum entropy deconvolution process even without an encoder. Hu et al.
[121] established an integrated dynamic model of a multi-stage planetary gear system, including a root crack on the sun gear. The failure mechanism and dynamic characteristics of the tooth crack are surveyed by considering some nonlinear factors such as gear backlash, time-varying meshing stiffness, and comprehensive mesh errors. These dynamic characteristics were revealed by irregular expansion of the attractor, divergence of the phase trajectory, periodic pulses in the time series diagram, and sideband frequencies with the sun gear fault characteristic frequency. It is shown that the crack disturbance excited the system into chaos from a quasi-periodic state at the limited equilibrium rotational speed and reduced the instability of the system; therefore, during crack fault diagnosis, the chaotic motion was avoided to find the fault characteristic frequency.