
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Nikolaos Kladovasilakis | -- | 3906 | 2022-09-06 12:57:49 | | | |
| 2 | Peter Tang | + 262 word(s) | 4168 | 2022-09-07 04:11:23 | | |
Video Upload Options
One of the main advantages of Additive Manufacturing (AM) is the ability to produce topologically optimized parts with high geometric complexity. In this context, a plethora of architected materials was investigated and utilized in order to optimize the 3D design of existing parts, reducing their mass, topology-controlling their mechanical response, and adding remarkable physical properties, such as high porosity and high surface area to volume ratio.
1. Introduction
2. Theoretical Background of Architected Materials
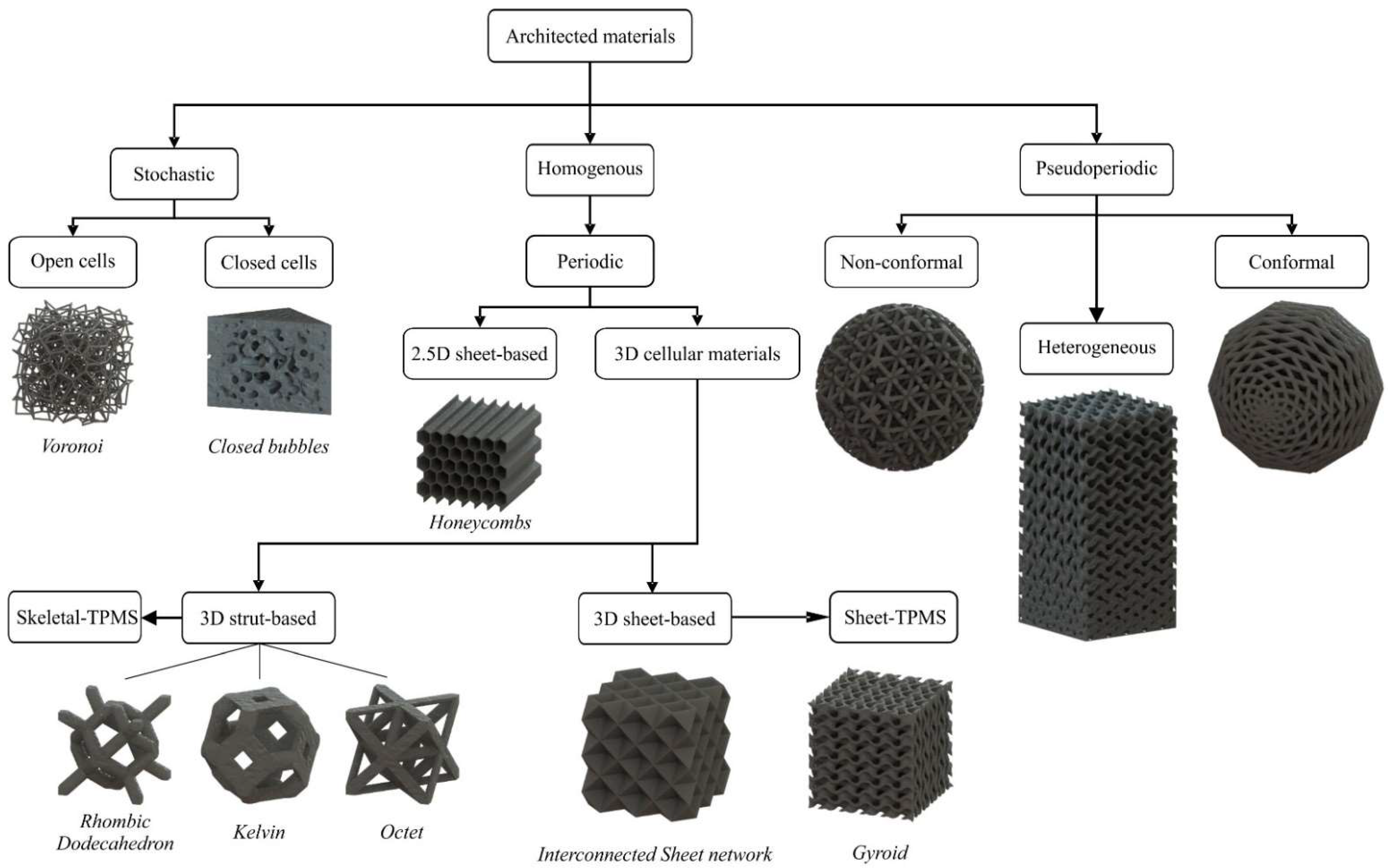
3. Classification of Architected Materials Based on the Geometry
4. Classification of Architected Materials Based on the Mechanical Response

5. Optimization of Architected Materials
The architected materials are employed in order to structurally optimize a part’s geometry by reducing the mass and providing a more uniform mass distribution. However, the implementation of architected materials could be enhanced by a series of methods that exploited the unique topological characteristics of the cellular materials. According to the existing literature [39][40][47][48][49][50], there are five widespread methods to optimize architected materials and lattice structures, which are also areas of extensive scientific interest.
The first and the most widespread method is named functionally gradation of the lattice structure. This technique is second-level topology optimization of an object, as in the first level the replacement of solid region by lattice structure was performed. In this second-level topology optimization, the relative density of a lattice structure is modified depending on the loads that the structure receives. In detail, for a specific application, the regions with low-stress concentration employ lattice structures with lower relative density in contrast with the regions with higher stress concentration [51]. In this way, the mechanical performance of the lattice structure is improved without changing the overall mass, as the mean relative density of the structure remains the same. The increment of the relative density in the structure could be employed rapidly, for example increasing from 10% to 60% relative density for two contiguities regions; or it could be performed gradually with linear, exponential, or scalar-field mode providing a smoother transaction between the regions of low and high relative densities. It is worth mentioning that the changes in relative density are achieved by changing the t/l ratio of the lattice structure, either by shifting the numerator or the denominator or even both; however, the most common way is by changing the lattices’ strut/wall thickness (numerator-t). Figure 3a illustrates an indicative implementation of functional graded architected materials (Gyroid) for impact and energy absorption experiments.
The second optimization method for the architected materials requires the utilization of one extra manufacturing process besides the additive manufacturing. The concept of this procedure is to replace the air inside the volume of an architected material with another material, as it is presented in Figure 3b. With this process, solid composite structures are created consisting of two materials the architected material and the filling material; these structures are also known as interpenetrating phase composites. There is a wide variety of filling materials from epoxy and silicone rubber compounds to polymer foams, such as polyurethane. Furthermore, the interpenetrating phase composites with architected materials could produce composite materials with unique physical and mechanical properties. For example, lattice structures with high electrical conductivity [52] or lattice structures with higher energy absorption rates [53].
The third technique is also very common among the research community and deploys two or more different architected materials inside the overall structure of a part. This method is also known as the hybridization of lattice structures [47]. More specifically, a different selection of architected materials is performed for a different region of the part with the objective to improve the mechanical response of the structure, but also to exploit the unique physical, mechanical, or aesthetic characteristics of the applied architected materials [54]. For example, auxetic architected materials could be deployed in regions where tensile stresses appear, and sheet-TPMS, such as the Schwarz Diamond structure, could be employed in the rest of the body in order to secure the structural integrity of the part. In addition, the hybridization lattice structures could be utilized in impact applications with remarkable results. This is achieved by maximizing the energy absorption of the whole structure with the combination of a bending-dominated architected material, which receives the maximum plastic deformation, with a stretching-dominated lattice structure, which receives elastic deformation with high peak strength. As in the functional gradation case, the hybridization process of a structure could be performed rapidly or gradually. Figure 3c illustrates a hybrid lattice designed for bending and energy absorption tests.
The fourth method fundamentally changes the unit cell structure of an architected due to the fact that it combines two or more architected materials in the volume of one unit cell in order to produce enhanced cellular material in terms of mechanical behavior [55]. Again, this is a hybridization method like the previous one with the difference that is performed at a level of a unit cell. In this method, the hybridization of the distinct cellular materials is performed by assessing the individual mechanical performance of two different architected materials and combining them. More specifically, the stress concentration regions of each structure are located, and the architected materials are combined in such a way to enhance and reinforce these regions leading to a new architected material with improved mechanical behavior. This method creates advanced cellular material with high geometry complexity that could be combined with the two aforementioned optimization methods of lattice structures for applications with high demands of structural integrity. Figure 3d shows unit cells of the hybrid architected materials coupled with the initial cellular materials and their contours of von-Mises stress which led to the proper combination of these structures.
The last technique leads to even more complex lattice structures, as it produces architected materials with higher-order structures [56]. In detail, a lattice structure is embedded within the elements of an architected material, i.e., strut/walls and nodes. Thus, these elements consist of lattice structures, as is portrayed in Figure 3e. This method is utilized in order to produce ultra-lightweight structures and structures with ultra-high porosity. However, the major challenge of this optimization method is the manufacturing procedure, as the lattice structures within the strut/surface volume are one order smaller than the whole structure. Thus, a 3D printer with sufficient build volume and high accuracy, such as the Selective Laser Melting (SLM) technique, is required, or a 3D printer with an ultra-high accuracy, such as the two-photon polymerization additive manufacturing technique.

References
- Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2003.
- Navez, T.; Schmidt, M.P.; Sigmund, O.; Pedersen, C.B.W. Topology optimization guided by a geometrical pattern library. Struct. Multidisc. Optim. 2022, 65, 108.
- Gebisa, A.W.; Lemu, H.G. A case study on topology optimized design for additive Manufacturing. IOP Conf. Ser. Mater. Sci. Eng. 2017, 276, 12026.
- Li, C.; Kim, I.Y.; Jeswiet, J. Conceptual and detailed design of an automotive engine cradle by using topology, shape, and size optimization. J. Struct. Multidiscip. Optim. 2015, 51, 547–564.
- Chen, Y.; Wang, Q.; Wang, C.; Gong, P.; Shi, Y.; Yu, Y.; Liu, Z. Topology Optimization Design and Experimental Research of a 3D-Printed Metal Aerospace Bracket Considering Fatigue Performance. Appl. Sci. 2021, 11, 6671.
- Tyflopoulos, E.; Lien, M.; Steinert, M. Optimization of Brake Calipers Using Topology Optimization for Additive Manufacturing. Appl. Sci. 2021, 11, 1437.
- Kladovasilakis, N.; Tsongas, K.; Tzetzis, D. Finite Element Analysis of Orthopedic Hip Implant with Functionally Graded Bioinspired Lattice Structures. Biomimetics 2020, 5, 44.
- Wu, P.-K.; Lee, C.-W.; Sun, W.-H.; Lin, C.-L. Biomechanical Analysis and Design Method for Patient-Specific Reconstructive Implants for Large Bone Defects of the Distal Lateral Femur. Biosensors 2022, 12, 4.
- Michell, A.G.M. The limits of economy of material in frame-structures. Philos. Mag. 1904, 8, 589–597.
- Prathyusha, A.L.R.; Raghu Babu, G. A review on additive manufacturing and topology optimization process for weight reduction studies in various industrial applications. Mater. Today Proc. 2022, 62, 109–117.
- Rosen, D.W. Research supporting principles for design for additive manufacturing. J. Virtual Phys. Prototyp. 2014, 9, 225–232.
- Larsen, S.D.; Sigmund, O.; Groen, J.P. Optimal truss and frame design from projected homogenization-based topology optimization. J. Struct. Multidiscip. Optim. 2018, 57, 1461–1474.
- Tyflopoulos, E.; Steinert, M. Topology and Parametric Optimization-Based Design Processes for Lightweight Structures. Appl. Sci. 2020, 10, 4496.
- Tyflopoulos, E.; Flem, D.T.; Steinert, M.; Olsen, A. State of the art of generative design and topology optimization and potential research needs. In Proceedings of the DS 91: NordDesign 2018, Linköping, Sweden, 14–17 August 2018.
- Xie, Y.M.; Huang, X. Recent developments in evolutionary structural optimization (ESO) for continuum structures. IOP Conf. Ser. Mater. Sci. Eng. 2010, 10, 012196.
- Wang, M.Y.; Wang, X.; Guo, D. A level set method for structural topology optimization. Comput. Methods Appl. Mech. Eng. 2003, 192, 227–246.
- Hoang, V.N.; Tran, P.; Vu, V.T.; Nguyen-Xuan, H. Design of lattice structures with direct multiscale topology optimization. Compos. Struct. 2020, 252, 112718.
- Pan, C.; Han, Y.; Lu, J. Design and Optimization of Lattice Structures: A Review. Appl. Sci. 2020, 10, 6374.
- Gibson, L.J.; Ashby, M.F. Cellular Solids. Structure and Properties; Cambridge University Press: Cambridge, UK, 1997.
- Al-Ketan, O.; Rowshan, R.; Al-Rub, R.K.A. Topology-Mechanical Property Relationship of 3D Printed Strut, Skeletal, and Sheet Based Periodic Metallic Cellular Materials. J. Addit. Manuf. 2018, 19, 167–183.
- Mantovani, S.; Giacalone, M.; Merulla, A.; Bassoli, E.; Defanti, S. Effective Mechanical Properties of AlSi7Mg Additively Manufactured Cubic Lattice Structures. 3D Print. Addit. Manuf. 2021. ahead of print.
- Deshpande, V.S.; Ashby, M.F.; Fleck, N.A. Foam topology: Bending versus stretching dominated architectures. Acta Mater. 2001, 49, 1035–1040.
- Abou-Ali, A.M.; Al-Ketan, O.; Rowshan, R.; Al-Rub, R.K.A. Mechanical Response of 3D Printed Bending-Dominated Ligament-Based Triply Periodic Cellular Polymeric Solids. J. Mater. Eng. Perform. 2019, 28, 2316–2326.
- Ashby, M.F. The properties of foams and lattices. Phil. Trans. R. Soc. A 2006, 364, 15–30.
- Elsayed, M.S.A.; Pasini, D. Analysis of the elastostatic specific stiffness of 2D stretching-dominated lattice materials. Mech. Mater. 2010, 42, 709–725.
- Gibson, L.J. Modelling the mechanical behavior of cellular materials. Mater. Sci. Eng. A 1989, 110, 1–36.
- Kladovasilakis, N.; Tsongas, K.; Kostavelis, I.; Tzovaras, D.; Tzetzis, D. Effective Mechanical Properties of Additive Manufactured Strut-Lattice Structures: Experimental and Finite Element Study. Adv. Eng. Mater. 2021, 24, 2100879.
- Kladovasilakis, N.; Tsongas, K.; Kostavelis, I.; Tzovaras, D.; Tzetzis, D. Effective mechanical properties of additive manufactured triply periodic minimal surfaces: Experimental and finite element study. Int. J. Adv. Manuf. Technol. 2022, 121, 7169–7189.
- Deshpande, V.S.; Fleck, N.A.; Ashby, M.F. Effective properties of the octet-truss lattice material. J. Mech. Phys. Solids 2001, 49, 1747–1769.
- Pei, E.; Kabir, I.; Breški, T.; Godec, D.; Nordin, A. A review of geometric dimensioning and tolerancing (GD&T) of additive manufacturing and powder bed fusion lattices. Prog. Addit. Manuf. 2022.
- Kanwar, S.; Al-Ketan, O.; Vijayavenkataraman, S. A novel method to design biomimetic, 3D printable stochastic scaffolds with controlled porosity for bone tissue engineering. Mater. Des. 2022, 220, 110857.
- Groth, J.H.; Anderson, C.; Magnini, M.; Tuck, C.; Clare, A. Five simple tools for stochastic lattice creation. Addit. Manuf. 2022, 49, 102488.
- Mirzaali, M.J.; Hedayati, R.; Vena, P.; Vergani, L.; Strano, M.; Zadpoor, A.A. Rational design of soft mechanical metamaterials: Independent tailoring of elastic properties with randomness. Appl. Phys. Lett. 2017, 111, 051903.
- Gibson, I.; Rosen, D.W.; Stucker, B. Additive Manufacturing Technologies; Springer: New York, NY, USA, 2010.
- Derveni, F.; Gross, A.J.; Peterman, K.D.; Gerasimidis, S. Postbuckling behavior and imperfection sensitivity of elastic–plastic periodic plate-lattice materials. Extrem. Mech. Lett. 2022, 50, 101510.
- Dong, Z.; Zhao, X. Application of TPMS structure in bone regeneration. Eng. Regen. 2021, 2, 154–162.
- Corona-Castuera, J.; Rodriguez-Delgado, D.; Henao, J.; Castro-Sandoval, J.C.; Poblano-Salas, C.A. Design and Fabrication of a Customized Partial Hip Prosthesis Employing CT-Scan Data and Lattice Porous Structures. ACS Omega 2021, 6, 6902–6913.
- Dong, G.; Tang, Y.; Zhao, Y.F. A survey of modeling of lattice structures fabricated by additive manufacturing. J. Mech Des. Trans. ASME 2017, 139, 100906.
- Al-Ketan, O.; Al-Rub, R.K.A. Multifunctional Mechanical Metamaterials Based on Triply Periodic Minimal Surface Lattices. Adv. Eng. Mater. 2019, 21, 1900524.
- Al-Ketan, O.; Rezgui, R.; Rowshan, R.; Du, H.; Fang, N.X.; Abu Al-Rub, R.K. Microarchitected Stretching-Dominated Mechanical Metamaterials with Minimal Surface Topologies. Adv. Eng. Mater. 2018, 20, 1800029.
- Farajzadeh Khosroshahi, S.; Tsampas, S.A.; Galvanetto, U. Feasibility study on the use of a hierarchical lattice architecture for helmet liners. Mater. Today Commun. 2018, 14, 312–323.
- Ferro, C.G.; Varetti, S.; De Pasquale, G.; Maggiore, P. Lattice structured impact absorber with embedded anti-icing system for aircraft wings fabricated with additive SLM process. Mater. Today Commun. 2018, 15, 185–189.
- Nasim, M.; Galvanetto, U. Mechanical characterisation of additively manufactured PA12 lattice structures under quasi-static compression. Mater. Today Commun. 2021, 29, 102902.
- González-Henríquez, C.M.; Sarabia-Vallejos, M.A.; Rodriguez-Hernandez, J. Polymers for additive manufacturing and 4D-printing: Materials, methodologies, and biomedical applications. J. Polym. Sci. 2019, 94, 57–116.
- Zheng, X.; Guo, X.; Watanabe, I. A mathematically defined 3D auxetic metamaterial with tunable mechanical and conduction properties. Mater. Des. 2021, 198, 109313.
- Sun, L.; Huang, W.M.; Ding, Z.; Zhao, Y.; Wang, C.C.; Purnawali, H.; Tang, C. Stimulus-responsive shape memory materials: A review. Mater. Des. 2012, 33, 577–640.
- Novak, N.; Al-Ketan, O.; Borovinšek, M.; Krstulović-Opara, L.; Rowshan, R.; Vesenjak, M.; Ren, Z. Development of novel hybrid TPMS cellular lattices and their mechanical characterization. J. Mater. Res. Technol. 2021, 15, 1318–1329.
- Chen, Z.; Xie, Y.M.; Wu, X.; Wang, X.; Li, Q.; Zhou, S. On hybrid cellular materials based on triply periodic minimal surfaces with extreme mechanical properties. J. Mater. Des. 2019, 183, 108109.
- Al-Ketan, O.; Assad, M.A.; Al-Rub, R.K.A. Mechanical properties of periodic interpenetrating phase composites with novel architected microstructures. Compos. Struct. 2017, 176, 9–19.
- Bauer, J.; Meza, L.R.; Schaedler, T.A.; Schwaiger, R.; Zheng, X.; Valdevit, L. Nanolattices: An Emerging Class of Mechanical Metamaterials. Adv. Mater. 2017, 29, 1701850.
- Mahmoud, D.; Elbestawi, M.A. Lattice Structures and Functionally Graded Materials Applications in Additive Manufacturing of Orthopedic Implants: A Review. J. Manuf. Mater. Process. 2017, 1, 13.
- Berhanu, S.; Tariq, F.; Jones, T.S.; McComb, D.W. Three-dimensionally interconnected organic nanocomposite thin films: Implications for donor–acceptor photovoltaic applications. J. Mater. Chem. 2010, 20, 8005–8009.
- Liu, Y.; Duan, D.L.; Jiang, S.L.; Li, S. Preparation and its cavitation performance of nickel foam/epoxy/SiC co-continuous composites. Wear 2015, 332–333, 979–987.
- Cui, L.; Jiang, F.; Deng, D.; Xin, T.; Sun, X.; Mousavian, R.T.; Peng, R.L.; Yang, Z.; Moverare, J. Cyclic response of additive manufactured 316L stainless steel: The role of cell structures. Scr. Mater. 2021, 205, 114190.
- Sun, Z.P.; Guo, Y.B.; Shim, V.P.W. Characterisation and modeling of additively-manufactured polymeric hybrid lattice structures for energy absorption. Int. J. Mech. Sci. 2021, 191, 106101.
- Yin, S.; Chen, H.; Li, J.; Yu, T.X.; Xu, J. Effects of architecture level on mechanical properties of hierarchical lattice materials. Int. J. Mech. Sci. 2019, 157–158, 282–292.




