Cube Surface Light Field Representation

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Xiaofei Ai	--	1612	2022-07-30 07:06:46	\|
2	layout	Camila Xu	Meta information modification	1612	2022-08-01 04:00:37	\|

This entry is adapted from the peer-reviewed paper 10.3390/app12147212

The core idea of the cube surface light field representation is to parameterize the light rays on the two intersections with the cube surface and use the color value at the first intersection of the light ray and the object's surface to be the color of this light ray, constructing a pure ray-based 4D light field representation of the scenes.

image-based rendering light field texture mapping

1. Introduction

Image-based rendering is a technique of generating a rendering result of an unknown viewpoint by interpolating through the collected image dataset ^[1]. One of its research motivations is the free-viewpoint rendering, i.e., to synthesize images at arbitrary viewpoints from discrete as well as sparse pre-captured images using appropriate transformations ^[2]^[3]. This kind of method does not require building three-dimensional (3D) mesh models of the scene in advance, and has broad application prospects in content generation, especially in the field of virtual reality and augmented reality (VR/AR). However, existing free-viewpoint rendering mainly adopts either the traditional image-based methods or the learning-based frameworks, and there are still many problems to be further studied.

One of the problems is the limited viewpoint freedom. The core of traditional image-based methods is the multidimensional representation of the light field ^[4] which describes the intensities of light rays passing through any viewpoints and any directions in free space. Restricting the light field in different dimensions can derive different kinds of light field representations, thus limiting the freedom of viewpoint to varying extents. For example, the two-parallel-plane parameterized (2PP) four-dimensional (4D) light field L(u, v, s, t) limits the viewpoints on a specific plane (camera plane) ^[5]^[6]. The 3D light field, such as the concentric mosaic, limits the viewpoints to a specific viewing circle (camera circle) ^[7]^[8]^[9]^[10]. The simplest 2D light field representation, i.e., the panorama limits the viewpoints to a single projection center ^[11]^[12]^[13]^[14]. The constraint on viewpoint freedom is helpful to simplify the dimensions of the light field model as well as reduce its data complexity. However, the free-viewpoint rendering pursues that the desired images can be rendered at arbitrary positions and orientations in the observation space. The above methods limit the degree of freedom (DoF) of the viewpoints so that the systems based on these methods only provide restricted viewpoints which does not satisfy the natural interaction between human and the real-world scenes.

Another problem is the poor time performance of novel view rendering. With the rapid progress of deep learning, some researchers use the learning-based frameworks to generate arbitrary views ^[15]^[16]^[17]^[18], trying to alleviate the restriction of the DoF of the viewpoints. However, this kind of method requires a complex training process, expensive network computation and takes a lot of time as well as memory for generating a high-resolution novel view, which cannot guarantee the real-time rendering performance. Both of these two issues have to be solved in the applications of free-viewpoint rendering in VR/AR. Only by providing a full viewpoint coverage in the observation space as well as the real-time rendering performance, can the requirement of content generation in VR/AR be met ^[19].

2. Cube Surface Light Field Representation

Figure 1. The cube surface light field representation. The parameters of each light ray are defined by the two intersections (A and B) with the cube surface and the ray's colors are defined by the RGB color at the first intersection with the object's surface.

The light rays in free space can be divided into two categories. The first category of light ray does not intersect with the objects in the scene, and almost does not influence the objects' appearance. The second category of light ray intersects with the scene's objects and has a significant impact on the objects' appearance, resulting in light and dark effects on the objects' surfaces. The origination of such light rays either can be from one or more light sources or can be the reflected light rays on the surface of an adjacent object. In particular, the images captured by a camera have already encoded the final impact of the light rays from these two originations on the appearance of the scene. Therefore, only the second category of light ray is concerned in the study of free-viewpoint rendering, and researchers do not distinguish whether the light ray is from the light source or the reflection from the adjacent objects' surface.

The cube surface light field uses a unified cube geometry to parameterize the set of the second category of light ray in free space and uses the pairs of intersected points on the cube surface to be the parameters of light rays. Researchers define that the center of the cube geometry is located at the origination of the 3D Cartesian coordinate system (CCS), and the edge length is the same as the size of the scene's bounding box. According to the twelve edges of the cube geometry, its surface can be divided into six sub-planes, corresponding to +X, +Y, +Z, −X, −Y, −Z planes, respectively. Therefore, the cube surface can be defined by a 2D function composed of six sub-planes, as shown in Equation (1), in which (x, y) refers to the 2D coordinates of the interior points on each sub-plane.

\begin{matrix} C : \sum_{i = 1}^{6} Π_{i} (x, y) \subset R^{2} \end{matrix}

On the cube surface, the origination of each light ray is defined by the 2D coordinates at the first intersections with the light rays and the cube surface, and the directions of the light rays are defined by the 2D coordinate at the second intersections with the light rays and the cube surface. The color values of each light ray are defined as the color at the first intersections with the light rays and the scenes, which are described by the RGB color representation. Consequently, the cube surface light field can be defined as a set of RGB color values of the light rays parameterized by the intersection pairs with a specific cube surface, as shown in Equation (2), in which m and n refer to the serial number of the sub-plane where the originations and directions of the light rays are parameterized. Similarly, (u, v) and (s, t) refer to the 2D coordinates of arbitrary interior points on the m-th sub-plane and on the n-th sub-plane, respectively.

L : \sum_{m = 1}^{6} (Π_{m} (u, v) \times \sum_{n = 1}^{6} Π_{n} (s, t)) \to RGB

Obviously, for all the light rays that intersect with the scene, the two intersections with the cube surface cannot be on the same sub-plane of the cube surface. Therefore, m and n must not get the same value at the same time in the cube surface light field. According to Equation (2), each light ray has been defined as a six-tuple (m, u, v, n, s, and t) so far. Since m and n are both enumeration values, their definition domains are integers between [1, 6]. To facilitate the parametric representation of the light field, the cube surface, as shown in Figure 2a can be expanded along any of its twelve edges, producing different cube map layouts, such as vertical and horizontal cross layouts, as shown in Figure 2b. Researchers use the horizontal layout as shown in Figure 2c to present each sub-view of the cube surface light field.

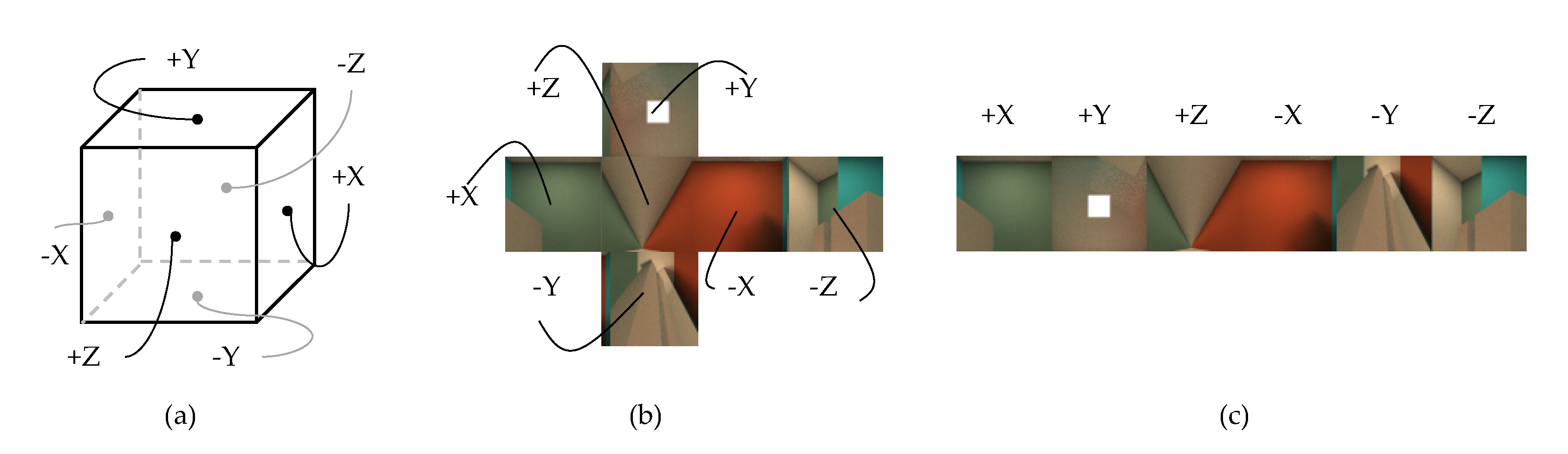Figure 2. The different layouts of cube map. (a) six face are marked by +X to −Z, (b) the cross layout and (c) the horizontal layout.

Intuitively, the texture coordinates can be used to further simplify Equation (2), resulting in the final representation of the cube surface light field denoted by Equation (3). Seeing from the dimension of u and v, each coordinate (u, v) represents a set of light rays from a fixed position, which can be described as a light field sub-view like in the traditional 2PP light field representation. Meanwhile, seeing from the dimension of s and t, each coordinate (s, t) represents a set of light rays from a fixed direction, which can be described as a sub-aperture image like in the 2PP light field representation.

L : I (u, v) \times I (s, t) \to RGB

One advantage of the cube surface parameterization is that it is easy to sample the light field. The two adjacent edges of each sub-plane are divided into several segments uniformly or non-uniformly. By connecting the endpoints of the two opposite segments, the sub-plane can be subdivided into several small square or rectangular blocks. The barycentric coordinates of each square or rectangular can be selected as the sampling points of the cube surface light field. This representation also helps to compress the light field images at each sampling point. The images generated by the sampling points on the same sub-plane have only translational transformation in both horizontal and vertical directions. If the equidistant sampling strategy is adopted in the sampling stage, the relationship between the image pixels of these viewpoints is easy to be quantitatively described by parallax, which facilitates the prediction and compression of adjacent views. It is also conducive to subsequent rendering, i.e., the light field rendering of an arbitrary scene only requires drawing a simple unit cube geometric. By intersecting the desired light rays with the cube surface, the light ray's parameters can be computed and used to query the color value of the novel viewpoint pixels. The computational consumption for testing intersection with the light rays and cube surface is relatively low, which makes the cube surface light field rendering possible to achieve real-time performance.

References

Cha Zhang; Tsuhan Chen; A survey on image-based rendering—representation, sampling and compression. Signal Processing: Image Communication 2004, 19, 1-28, 10.1016/j.image.2003.07.001.
Alvaro Collet; Ming Chuang; Pat Sweeney; Don Gillett; Dennis Evseev; David Calabrese; Hugues Hoppe; Adam G. Kirk; Steve Sullivan; High-quality streamable free-viewpoint video. ACM Transactions on Graphics 2015, 34, 1-13, 10.1145/2766945.
Peter Hedman; Julien Philip; True Price; Jan-Michael Frahm; George Drettakis; Gabriel Brostow; Deep blending for free-viewpoint image-based rendering. ACM Transactions on Graphics 2018, 37, 1-15, 10.1145/3272127.3275084.
Michael Landy; J. Anthony Movshon; The Plenoptic Function and the Elements of Early Vision. null 1991, 1, 2-20, 10.7551/mitpress/2002.003.0004.
Marc Levoy; Pat Hanrahan; Light field rendering. Proceedings of the 23rd annual conference on Computer graphics and interactive techniques - SIGGRAPH '96 1996, 1, 31-42, 10.1145/237170.237199.
Ben Mildenhall; Pratul P. Srinivasan; Rodrigo Ortiz-Cayon; Nima Khademi Kalantari; Ravi Ramamoorthi; Ren Ng; Abhishek Kar; Local Light Field Fusion: Practical View Synthesis with Prescriptive Sampling Guidelines. null 2019, 38, 1-12.
Heung-Yeung Shum; Li-Wei He; Rendering with concentric mosaics. Proceedings of the 26th annual conference on Computer graphics and interactive techniques - SIGGRAPH '99 1999, 1, 299-306, 10.1145/311535.311573.
Heung-Yeung Shum; King-To Ng; Shing-Chow Chan; A virtual reality system using the concentric mosaic: construction, rendering, and data compression. IEEE Transactions on Multimedia 2005, 7, 85-95, 10.1109/tmm.2004.840591.
Ryan S. Overbeck; Daniel Erickson; Daniel Evangelakos; Matt Pharr; Paul Debevec; A system for acquiring, processing, and rendering panoramic light field stills for virtual reality. ACM Transactions on Graphics 2018, 37, 1-15, 10.1145/3272127.3275031.
Peter Hedman; Tobias Ritschel; George Drettakis; Gabriel J. Brostow; Scalable inside-out image-based rendering. ACM Transactions on Graphics 2016, 35, 1-11, 10.1145/2980179.2982420.
Richard Szeliski; Image Alignment and Stitching: A Tutorial. Foundations and Trends® in Computer Graphics and Vision 2007, 2, 1-104, 10.1561/0600000009.
Julius Surya Sumantri; In Kyu Park; 360 Panorama Synthesis from a Sparse Set of Images on a Low-Power Device. IEEE Transactions on Computational Imaging 2020, 6, 1179-1193, 10.1109/tci.2020.3011854.
Christian Richardt; Yael Pritch; Henning Zimmer; Alexander Sorkine-Hornung; Megastereo: Constructing High-Resolution Stereo Panoramas. 2013 IEEE Conference on Computer Vision and Pattern Recognition 2013, 1, 1256-1263, 10.1109/cvpr.2013.166.
Ching-Ling Fan; Wen-Chih Lo; Yu-Tung Pai; Cheng-Hsin Hsu; A Survey on 360° Video Streaming. ACM Computing Surveys 2020, 52, 1-36, 10.1145/3329119.
Ben Mildenhall; Pratul P. Srinivasan; Matthew Tancik; Jonathan T. Barron; Ravi Ramamoorthi; Ren Ng; NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. null 2020, 1, 405-421, 10.1007/978-3-030-58452-8_24.
Lingjie Liu; Jiatao Gu; Kyaw Zaw Lin; Tat-Seng Chua; Christian Theobalt; Neural Sparse Voxel Fields. NeurIPS 2020 2020, 1, 15651–15663.
Stephen Lombardi; Tomas Simon; Jason Saragih; Gabriel Schwartz; Andreas Lehrmann; Yaser Sheikh; Neural Volumes: Learning Dynamic Renderable Volumes from Images. ACM Trans. Graph 2019, 38, 1-12.
Vincent Sitzmann; Justus Thies; Felix Heide; Matthias NieBner; Gordon Wetzstein; Michael Zollhofer; DeepVoxels: Learning Persistent 3D Feature Embeddings. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) 2019, 1, 2432-2441, 10.1109/cvpr.2019.00254.
Christian Richardt, James Tompkin, Gordon Wetzstein. Real VR – Immersive Digital Reality; Marcus Magnor, Alexander Sorkine-Hornung, Eds.; Springer: Cham, Switzerland, 2022; pp. 3-32.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Computer Science, Artificial Intelligence

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Xiaofei Ai

Yigang Wang

View Times: 339

Update Date: 01 Aug 2022

Table of Contents

Video Upload Options

Confirm

1. Introduction

2. Cube Surface Light Field Representation

References