Your browser does not fully support modern features. Please upgrade for a smoother experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Lu, J.; , Y.; , Q.; Liu, Y.; Lu, J. Jump Point Search Algorithm. Encyclopedia. Available online: https://encyclopedia.pub/entry/24246 (accessed on 01 March 2026).
Lu J, Y, Q, Liu Y, Lu J. Jump Point Search Algorithm. Encyclopedia. Available at: https://encyclopedia.pub/entry/24246. Accessed March 01, 2026.
Lu, Jiakai, Yuanluo , Qiongqin , Yanyu Liu, Jiakai Lu. "Jump Point Search Algorithm" Encyclopedia, https://encyclopedia.pub/entry/24246 (accessed March 01, 2026).
Lu, J., , Y., , Q., Liu, Y., & Lu, J. (2022, June 21). Jump Point Search Algorithm. In Encyclopedia. https://encyclopedia.pub/entry/24246
Lu, Jiakai, et al. "Jump Point Search Algorithm." Encyclopedia. Web. 21 June, 2022.
Copy Citation
The JPS algorithm is a pathfinding algorithm that uses pruned neighbor rules as the search direction of nodes and the position of forced neighbors as the judgment of jump points.
path planning
robot trajectory optimization
JPS algorithm
1. Background
Initially, the use of mobile robots was limited to manufacturing. However, with the development of technology and innovation, mobile robots are now commonly used in various industries such as medical [1], mining, rescue, military, education, agriculture [2] and service industries [3].
From the perspective of mobile robots, the real point is to move from a designed starting point to another target point and the need to smoothly avoid obstacles in a path-optimal manner [4]. Therefore, the navigation of mobile robots is crucial for mobile robots [5]. Sarif and Buniyamin pointed out that path planning is the main problem of mobile robots and an important component of navigation [6]. The result of path planning will intuitively have an impact on how well the robot completes the task in real time and how well the result is achieved.
From the present point of view, path planning algorithms are favored by many researchers with the rise of mobile robots, UAVs [7][8][9], the unmanned field [10][11], and the video game field [12]. However, the study of path planning for mobile robots, especially the trajectory optimization of generated paths, remains a great challenge. For example, Figure 1 shows a robot and its target location. The solid path is a path consisting of straight lines and sharp turns at points A, B, C, and D. It is also the path generated for the discrete map state due to the fixed pathfinding direction. This path is not ideal for the movement of a mobile robot. First, mobile robots cannot make sudden sharp turns and need to slow down. For example, for driverless cars, sudden turns between path nodes and discontinuities in speed and acceleration are very dangerous behaviors for passengers [13][14]. For intelligent wheelchair robots, there are interruptions and sharp turns among the paths, which may cause secondary injuries for the patient [15][16]. Second, fixing the robot’s search direction is not suitable for finding the shortest or optimal path, which makes many possible paths in the map ignored by the robot. As shown by the dashed line in Figure 1, a shorter path means higher efficiency and less energy consumption while ensuring the safety of the mobile robot. For example, in unmanned warehousing as well as in the workshop transportation process, the efficiency of the transport robot will directly affect the overall operational efficiency of the warehouse and workshop [17].
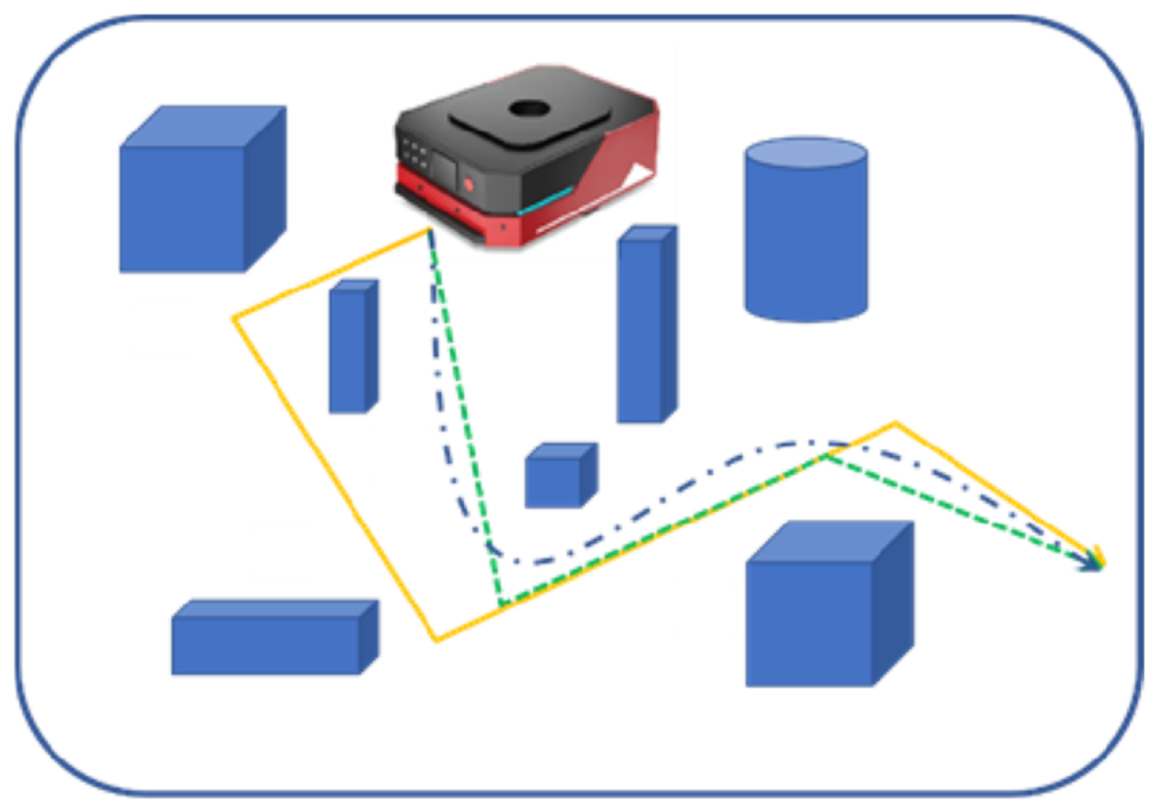 Figure 1. Non-smooth path for mobile robots.
Figure 1. Non-smooth path for mobile robots.To solve these problems, any-angle path planning [18] and path smoothing techniques [19] need to be introduced. Path smoothing is an important issue in path finding for mobile robots. Smooth paths need to satisfy the constraints of continuity such as path position, robot movement speed, and acceleration. At the same time, in order to ensure that the mobile robot finds the shortest path in the path finding process, the any-angle path planning is needed to no longer restrict the search direction of the mobile robot.
2. Related Work
Path planning for mobile robots is actually the selection of a shortest obstacle avoidance path in the task area that can be connected from the starting point to the end point. The essence of this is the problem of optimal solution of the path [20]. The path planning should fully take into account the feasibility constraints that arise during the practical application of the robot [21]. More precisely, the path generated by the path planning algorithm of the mobile robot should satisfy the shortest and most efficient path with continuous and smooth transition of the path node states (position, velocity, acceleration and other information).
Various path optimization methods have been developed in previous studies. Among the most intuitive methods for path smoothness optimization are Bessel curves [22] and B spline curve optimization [23]. This approach allows curve fitting using trajectory control points in the path generation phase to achieve path smoothing. Usually, the initial number of control points obtained by the global path planning algorithm is low fitting, and the fitted paths are prone to re-collide with obstacles. To increase the curve fit, the path control points are usually added. However, a single increase in the number of control points can lead to a significant decrease in the efficiency of the algorithm [24]. In the research [13], a polynomial interpolation-based method is proposed to improve the continuity problem in the automatic parking process. Polynomial interpolation is a simple functional approach [25]. This method is solved by finding a polynomial containing all path nodes and adding continuity constraints for node positions, velocities, accelerations, etc. In addition, the polynomial interpolation method can be used to construct a Safe Flight Corridor (SFC) by generating collision avoidance linear constraints using the convex packet property of Bernstein polynomials as a further solution to the safety of mobile robots during operation [26].
The JPS method using heuristic search methods has been proposed in recent years driven by the efficiency of path planning for mobile robots. The classical JPS algorithm is built on the basis of the evaluation function of the A* algorithm, which improves the search efficiency of the A* algorithm by ignoring useless nodes and retaining only key nodes, thus greatly reducing the time consumption in the search process [27]. However, on the other hand, the JPS algorithm still cannot escape the limitation of the search direction imposed by the discretized grid map [28]. When planning a grid map, JPS usually plans from the center of each grid cell and only allows transitions to the center of adjacent grid cells. This will cause the JPS algorithm path direction variation to be limited to a multiple of II/4, resulting in a suboptimal path, as shown in Figure 2.
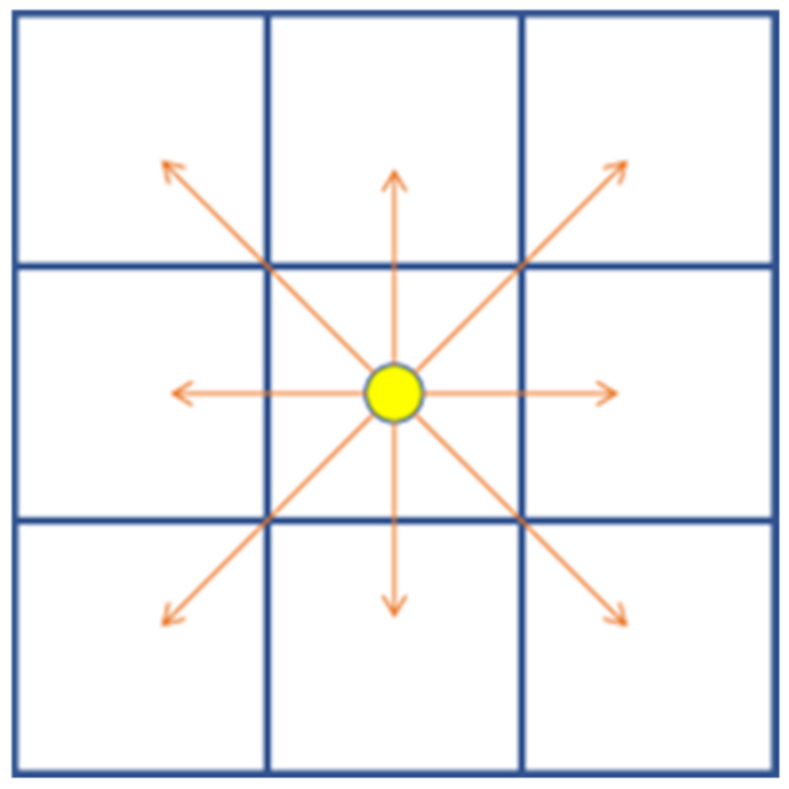 Figure 2. Limitations of search angle.
Figure 2. Limitations of search angle.3. JPS Algorithm
The JPS algorithm is a pathfinding algorithm that uses pruned neighbor rules as the search direction of nodes and the position of forced neighbors as the judgment of jump points. The JPS algorithm extends the jump points by iterative computation and by selecting the least costly node among the candidate jump points as the subsequent path. The JPS algorithm’s method of determining the current jump point x consists of the following three parts:
1. If node x is a start point or a target point, then node x is a jump point.
2. If node x has at least one forced neighbor, then node x is a jump point.
3. If the search direction from the parent node of node x to x is diagonal and there is a point in the horizontal or vertical direction of x that satisfies condition 1 and 2, then x is a jump point.
2. If node x has at least one forced neighbor, then node x is a jump point.
3. If the search direction from the parent node of node x to x is diagonal and there is a point in the horizontal or vertical direction of x that satisfies condition 1 and 2, then x is a jump point.
JPS Algorithm for Pruned Neighbor Rule and Forced Neighbors
In the JPS algorithm, the neighboring nodes in each direction need to be considered when searching from the starting node. When the JPS algorithm determines a specific search direction, it expands in that direction and does not need to calculate the generation value of nodes in that direction until it meets an obstacle or jump point. If a path is blocked, all nodes along that direction will be pruned without further consideration.
While JPS is extending a path in a particular direction, it identifies a set of natural neighbors for a node under evaluation. When the extension direction is a straight line, the natural neighbor of the current point x is defined as the next node in the same direction. That is, JPS will continue to search along the direction of the current natural neighbor. When the extension direction is diagonal, the natural neighbors of the current point x include three nodes, which are the next node along the extension diagonal, and the next vertical and horizontal nodes in the extension direction, as shown in Figure 3a,b. That is, JPS will start expanding in the direction of vertical and horizontal natural neighbors first until they are blocked or jump points are found before considering the search in the diagonal direction.
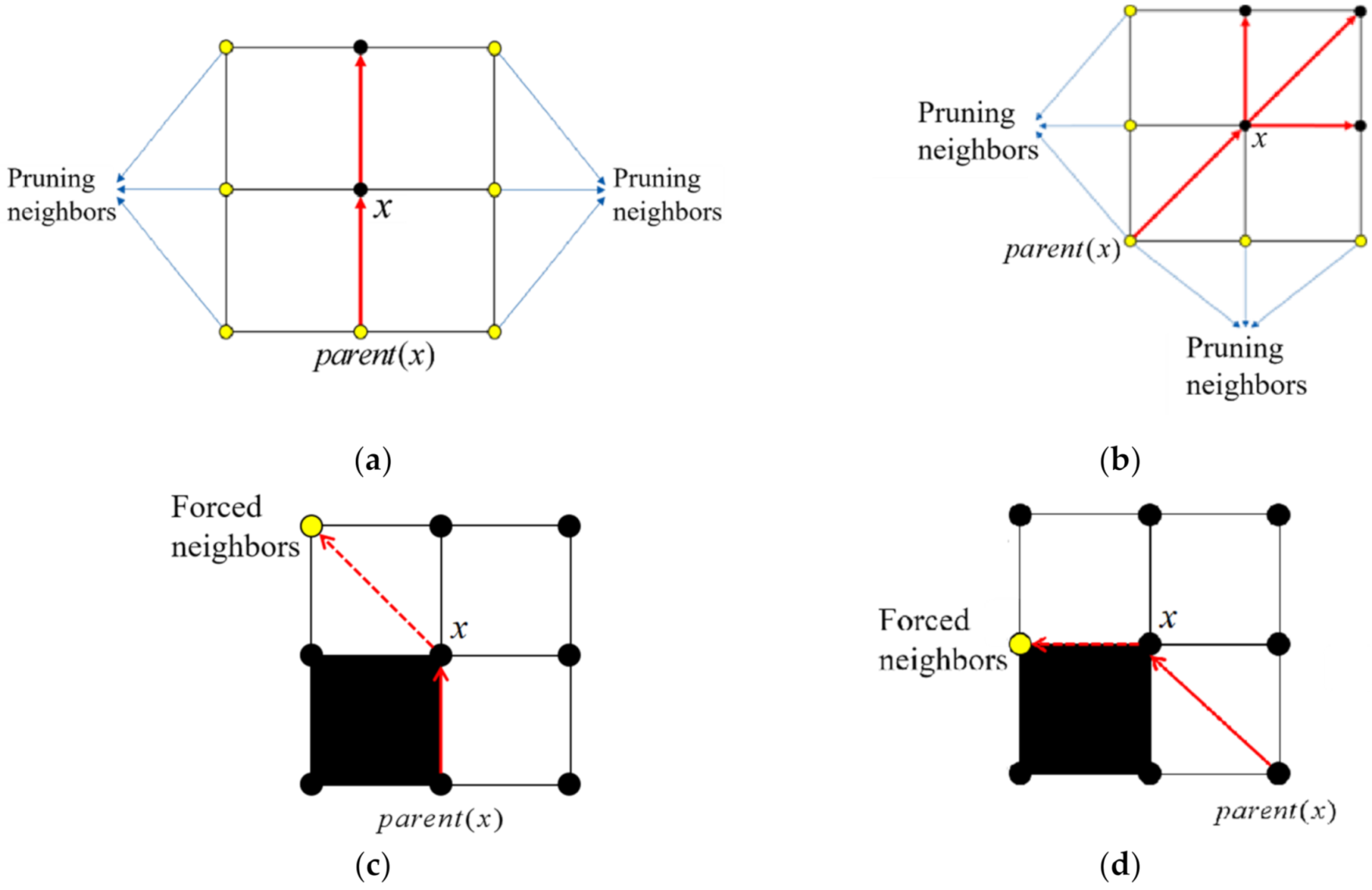 Figure 3. JPS algorithm for natural neighbors and forced neighbors. (a) pruning rule of JPS algorithm, (b) pruning rule of JPS algorithm, (c) the way to determine the forced neighbor nodes, (d) the way to determine the forced neighbor nodes.
Figure 3. JPS algorithm for natural neighbors and forced neighbors. (a) pruning rule of JPS algorithm, (b) pruning rule of JPS algorithm, (c) the way to determine the forced neighbor nodes, (d) the way to determine the forced neighbor nodes.In the JPS algorithm, the current node x has obstacles among its eight neighbors, and n is a non-obstacle, non-search direction neighbor node of the current node. Then, the distance cost of x’s parent node parent(x) to reach n through x is smaller than the distance cost of any path to reach n without going through x. Then, n is said to be a forced neighbor of x. If the current node is found to have forced neighbors, the node is identified as a jump point, and the expansion in the direction of forced neighbors must be considered, as shown in Figure 3c,d.
References
- Liu, G.; Liu, Y.; Zhao, J.; Zhu, L. Path planning for a new mine rescue robot base on visual tangent graphs. Jilin Daxue Xuebao 2011, 41, 1107–1112.
- Yang, C.; Liu, Y.; Wang, Y.; Xiong, L.; Xu, H.; Zhao, W. Research and Experiment on Recognition and Location System for Citrus Picking Robot in Natural Environment. Nongye Jixie Xuebao 2019, 50, 14–22+72.
- Oh, J.S.; Choi, Y.H.; Park, J.B.; Zheng, Y.F. Complete coverage navigation of cleaning robots using triangular-cell-based map. IEEE Trans. Ind. Electron. 2004, 51, 718–726.
- Atiyah, A.N.; Adzhar, N.; Jaini, N.I. An overview: On path planning optimization criteria and mobile robot navigation. J. Phys. Conf. Ser. 2021, 1988, 012036.
- Babunski, D.; Berisha, J.; Zaev, E.; Bajrami, X. Application of Fuzzy Logic and PID Controller for Mobile Robot Navigation. In Proceedings of the 9th Mediterranean Conference on Embedded Computing (MECO), Budva, Montenegro, 8–11 June 2020; pp. 21–36.
- Sariff, N.; Buniyamin, N. An overview of autonomous mobile robot path planning algorithms. In Proceedings of the 4th Student Conference on Research and Development, Shah Alam, Malaysia, 27–28 June 2006; pp. 183–188.
- Zhang, N.; Zhang, M.; Low, K.H. 3D path planning and real-time collision resolution of multirotor drone operations in complex urban low-altitude airspace. Transp. Res. Part C Emerg. Technol. 2021, 129, 103123.
- Ivić, S.; Crnković, B.; Grbčić, L.; Matleković, L. Multi-UAV trajectory planning for 3D visual inspection of complex structures. arXiv 2022, arXiv:math/2204.10070.
- Pehlivanoglu, Y.V. A new vibrational genetic algorithm enhanced with a Voronoi diagram for path planning of autonomous UAV. Aerosp. Sci. Technol. 2012, 16, 47–55.
- Ayawli, B.B.K.; Chellali, R.; Appiah, A.Y.; Kyeremeh, F. An Overview of Nature-Inspired, Conventional, and Hybrid Methods of Autonomous Vehicle Path Planning. J. Adv. Transp. 2018, 2018, 8269698.
- Zhou, K.; Yu, L.; Long, Z.; Mo, S. Local path planning of driverless car navigation based on jump point search method under urban environment. Futue Internet 2017, 9, 51.
- Foderaro, G.; Swingler, A.; Ferrari, S. A model-based cell decomposition approach to on-line pursuit-evasion path planning and the video game Ms. Pac-Man. In Proceedings of the IEEE Conference on Computational Intelligence and Games (CIG), Granada, Spain, 11–14 September 2012; pp. 281–287.
- Hu, Q.; Wang, J.; Zhang, X. Optimized Parallel Parking Path Planning Based on Quintic Polynomial. Comput. Eng. Appl. 2022, 1–9. Available online: http://kns.cnki.net/kcms/detail/11.2127.TP.20210325.1007.008.html (accessed on 21 May 2022).
- Leiyan, Y.; Xianyu, W.; Zeyu, H.; Zaiyou, D.; Yufeng, Z.; Zhaoyang, M. Path Planning Optimization for Driverless Vehicle in Parallel Parking Integrating Radial Basis Function Neural Network. Appl. Sci. 2021, 11, 8178.
- Chen, L.; Wang, S.; Hu, H.; McDonald-Maier, K.; Fei, M. Novel path curvature optimization algorithm for intelligent wheelchair to smoothly pass a narrow space. Zidonghua Xuebao Acta Autom. Sin. 2016, 42, 1874–1885.
- Sahin, H.; Kavsaoglu, A. Indoor path finding and simulation for smart wheelchairs. In Proceedings of the 29th Signal Processing and Communications Applications Conference (SIU), Istanbul, Turkey, 9–11 June 2021; pp. 1–4.
- Hu, M.; Cao, J.; Chen, X.; Peng, F. Path planning of intelligent factory based on improved ant colony algorithm. In Proceedings of the Asia-Pacific Conference on Communications Technology and Computer Science (ACCTCS), Shenyang, China, 22–24 January 2021; pp. 1–4.
- Firmansyah, E.; Masruroh, S.; Fahrianto, F. Comparative analysis Of A and basic theta algorithm in android-based pathfmding games. In Proceedings of the 6th International Conference on Information and Communication Technology for The Muslim World (ICT4M), Jakarta, Indonesia, 22–24 November 2016; pp. 275–280.
- Geng, S.; Peng, S.; Han, Y. Research on motion planning of snake-like robot based on the interpolation function. In Proceedings of the 8th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), Hangzhou, China, 27–28 August 2016; pp. 81–84.
- Huo, F.; Chi, J.; Huang, Z.; Ren, L.; Sun, Q.; Chen, J. Review of Path Planning for Mobile Robots. Jilin Daxue Xuebao 2018, 36, 639–647.
- Ravankar, A.; Ravankar, A.; Kobayashi, Y.; Hoshino, Y.; Peng, C. Path smoothing techniques in robot navigation: State-of-the-art, current and future challenges. Sensors 2018, 18, 3170.
- Shi, J.; Su, Y.; Bu, C.; Fan, X. A mobile robot path planning algorithm based on improved A*. J. Phys. Conf. Ser. 2020, 1468, 032018.
- Foo, J.L.; Knutzon, J.; Kalivarapu, V.; Oliver, J.; Winer, E. Path planning of unmanned aerial vehicles using B-splines and particle swarm optimization. J. Aerosp. Comput. Inf. Commun. 2009, 6, 271–290.
- Elbanhawi, M.; Simic, M.; Jazar, R.N. Continuous Path Smoothing for Car-Like Robots Using B-Spline Curves. J. Intell. Robot. Syst. Theor. Appl. 2015, 80, 23–56.
- Huh, U.-Y.; Chang, S.A. G2 continuous path-smoothing algorithm using modified quadratic polynomial interpolation. Int. J. Adv. Rob. Syst. 2014, 11, 25.
- Liu, S.; Watterson, M.; Mohta, K.; Sun, K.; Bhattacharya, S.; Taylor, C.J.; Kumar, V. Planning dynamically feasible trajectories for quadrotors using safe flight corridors in 3-D complex environments. IEEE Robot. Autom. 2017, 2, 1688–1695.
- Harabor, D.; Grastien, A. Online graph pruning for pathfinding on grid maps. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 7–11 August 2011; Volume 25, pp. 1114–1119.
- Huang, J.; Wu, Y.; Lin, X. Smooth JPS Path Planning and Trajectory Optimization Method of Mobile Robot. Nongye Jixie Xuebao 2021, 52, 21–29+121.
More
Information
Subjects:
Robotics
Contributors
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
4.3K
Revisions:
3 times
(View History)
Update Date:
21 Jun 2022
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No





