
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Raffaele Guarasci | -- | 1911 | 2022-06-13 17:02:15 | | | |
| 2 | Catherine Yang | + 6 word(s) | 1917 | 2022-06-14 03:05:17 | | |
Video Upload Options
Quantum Natural Language Processing (QNLP) is a hybrid field that combines aspects derived from Quantum Computing (QC) with tasks of Natural Language Processing (NLP).
1. Introduction
2. NLP and Quantum: The Meeting Point
The Compositional Distributional Model
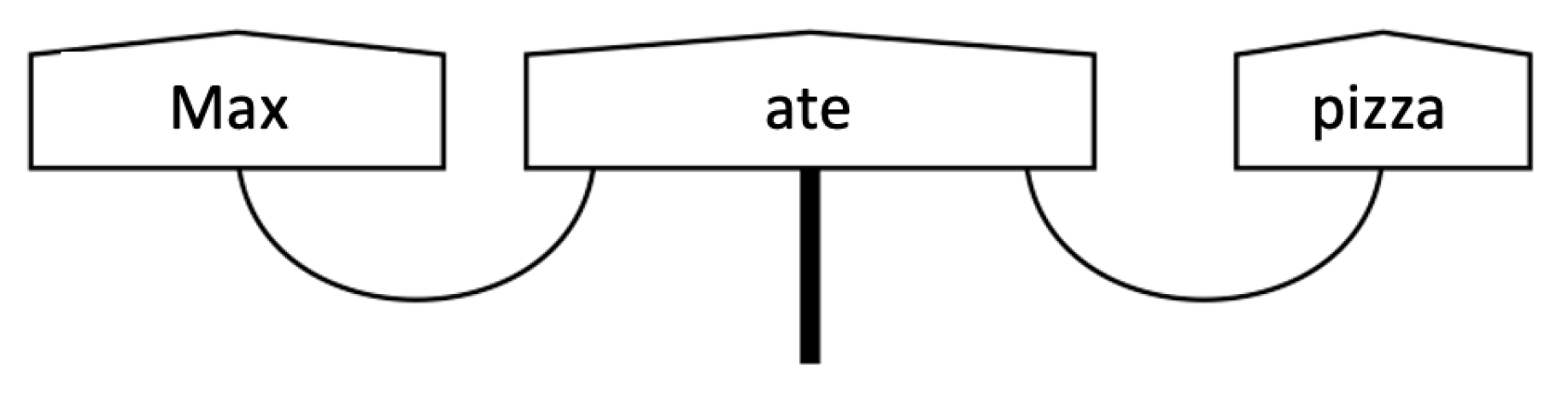
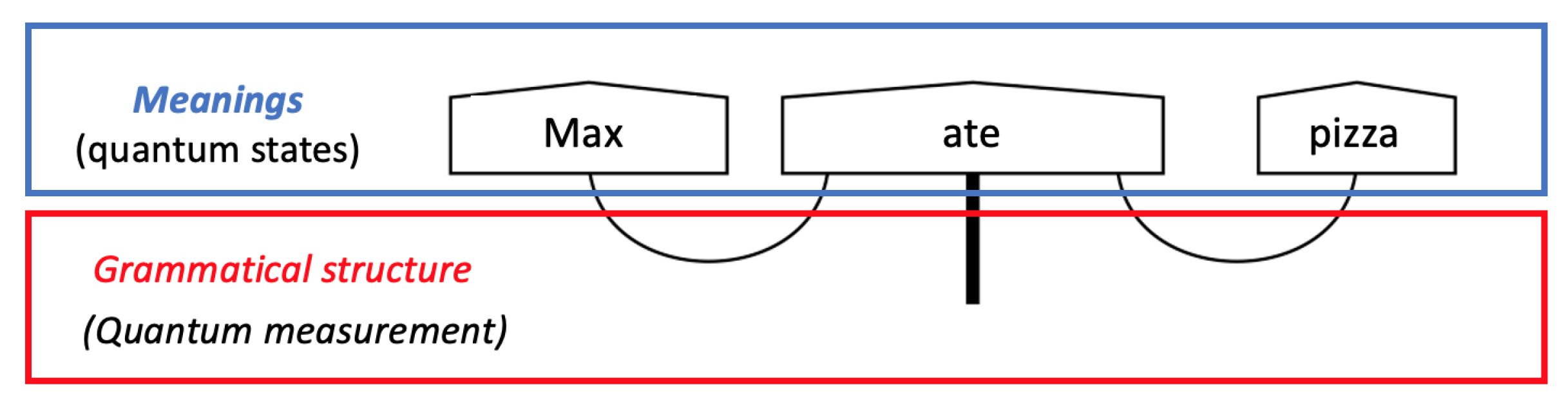
Different Approaches
QNLP has affected NLP in different ways since the release of the compositional distributional model. Early works have focused on specific linguistic issues and critical tasks of NLP. Subsequently, the focus shifted to more straightforward tasks that can be implemented on actual data and compared with existing benchmarks in the literature. Approaches can be classified as follows:
1. Theoretical Approaches: First QNLP approaches focused on formal aspects of natural language. These works propose algorithms based on QC for different NLP tasks. In these works, the methodological and performance advantages of QNLP algorithms have been theoretically demonstrated, based on the assumption of the theorized but never realized QRAM. Alternative approaches have been developed to overcome this shortcoming. Variational quantum circuits [36] or classical ansatz parameters[38] have been tested to encode distributional embedding.
2. Quantum-Inspired Approaches: a family of hybrid approaches exploiting quantum properties to address NLP tasks running on classical hardware. These approaches have the advantage that they can be implemented without having to rely on quantum hardware. In addition, these approaches can be tested on actual data and compared with benchmark datasets using classical metrics used to estimate performance. These approaches are mainly based on a density matrix defined in probabilistic quantum space. The density matrix has proven to be an effective way of representing and modeling language in different NLP tasks, encoding more semantic dependencies concerning classic word embeddings. This sub-field has attracted the most interest in the literature since different quantum language models (QLM) have been proposed for different tasks, ranging from Information Retrieval[39], Question Answering \cite, and Sentiment Classification \cite. Comparative visualization of the models proposed by the quantum-inspired works described below, including the datasets on which they have been tested; the performance achieved against the reference baselines are shown in Table 1.
| Task | Proposed Approach | Dataset | Metric | Score |
|---|---|---|---|---|
| Information retrieval | Quantum Language Model (QLM) [39] | SJMN | MAP | 0.2093 (0.271) |
| TREC7-8 | 0.2254 (0.2243) | |||
| WT10g | 0.2264 (0.2146) | |||
| ClueWeb-B | 0.1196 (0.1137) | |||
| Quantum Language Model-based Query Expansion (QLM-QE) [40] |
TREC 2013 | MAP@10 | 8.94 (4.91) | |
| TREC 2014 | 14.79 (14.52) | |||
| Quantum Interference-inspired Neural Matching model (QINM) [41] |
ClueWeb-B | MAP | 0.134 (0.082) | |
| Robust-04 | 0.294 (0.103) | |||
| Question answering | Neural Network-based Quantum-like Language Model (NNQLM) [42] |
TREC-QA | MAP | 0.758 (0.678) |
| WIKIQA | 0.649 (0.510) | |||
| Quantum Many-body Wave Function for Language Modeling (QMWF-LM) [43] |
TREC-QA | MAP | 0.752 (0.678) | |
| WIKIQA | 0.695 (0.512) | |||
| Complex-valued-Network (CNM) [44] | YahooQA | MAP | 0.575 (0.395) | |
| TREC-QA | 0.770 (0.777) | |||
| WIKIQA | 0.674 (0.652) | |||
| Sentiment classification | GQLM [45] | OMD | Accuracy | 0.629 (0.614) |
| SS-tweet | 0.618 (0.579) | |||
| Quantum-inspired Interactive Networks (QIN) [46] |
MELD | Accuracy | 0.679 (0.652) | |
| IEMOCAP | 0.376 (0.351) | |||
| TextTN [47] | MR | Accuracy | 82.2 (82.3) | |
| CR | 85.7 (85.4) | |||
| Subj | 95.3 (94.6) | |||
| MPQA | 90.4 (90.4) | |||
| BERT+TextTN [47] | SST-2 | Accuracy | 95.3 (96.7) | |
| SST-5 | 54.8 (54.7) |
3. Quantum-Computer Approaches: these approaches have been actually tested on real quantum hardware (NISQ devices CITE). These works are intended as the applied counterpart of theoretical works in which the mathematical foundations are provided. They start from the assumption that a quantum-based model of language should be closer and more reliable than current language models with respect to a specific task. Experiments have focused on simple NLP tasks. In particular, the first implementation of an NLP task on NISQ hardware has been proposed by [48], following theoretical methods proposed in [38]. The conceptual and mathematical foundations on which these works are based are described in [36]. It uses DisCoCat to perform a simple question-answering task on a small custom dataset, adopting the paradigm of Parameterized quantum circuits as machine learning models [49]. Subsequently, in [53], the first medium-scale NLP experiments running on quantum hardware have been performed. Two tasks are proposed, and both of them are structured as binary classification problems. The first one uses a dataset of 130 simple-syntax sentences generated from a fixed vocabulary using a simple CFG that can refer to one of two possible topics. For the second task, 105 noun phrases are extracted from the RelPron dataset [54], and the goal of the model is to predict whether a noun phrase contains a subject-based or an object-based relative clause. Finally, in [55], a preliminary experiment focused on machine translation using DisCoCat has been proposed. The goal of the experiment is the possibility of a quantum-like approach to language understanding in different languages. This is the first work trying to use DisCoCat for a language other than English.
References
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 6000–6010.
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), Minneapolis, MN, USA, 2–7 June 2019; Association for Computational Linguistics: Minneapolis, MN, USA, 2019; pp. 4171–4186.
- Radford, A.; Wu, J.; Child, R.; Luan, D.; Amodei, D.; Sutskever, I. Language models are unsupervised multitask learners. OpenAI Blog 2019, 1, 9.
- Clark, K.; Luong, M.T.; Le, Q.V.; Manning, C.D. ELECTRA: Pre-training Text Encoders as Discriminators Rather Than Generators. In Proceedings of the ICLR, Addis Ababa, Ethiopia, 26–30 April 2020.
- Zhu, J.; Xia, Y.; Wu, L.; He, D.; Qin, T.; Zhou, W.; Li, H.; Liu, T. Incorporating BERT into Neural Machine Translation. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019.
- Sun, C.; Qiu, X.; Xu, Y.; Huang, X. How to fine-tune bert for text classification? In Proceedings of the China National Conference on Chinese Computational Linguistics, Kunming, China, 18–20 October 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 194–206.
- Lee, K.; He, L.; Lewis, M.; Zettlemoyer, L. End-to-end Neural Coreference Resolution. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, Copenhagen, Denmark, 9–11 September 2017; Association for Computational Linguistics: Copenhagen, Denmark, 2017; pp. 188–197.
- Guarasci, R.; Minutolo, A.; Damiano, E.; De Pietro, G.; Fujita, H.; Esposito, M. ELECTRA for Neural Coreference Resolution in Italian. IEEE Access 2021, 9, 115643–115654.
- Guarasci, R.; Silvestri, S.; De Pietro, G.; Fujita, H.; Esposito, M. BERT syntactic transfer: A computational experiment on Italian, French and English languages. Comput. Speech Lang. 2022, 71, 101261.
- Guarasci, R.; Silvestri, S.; De Pietro, G.; Fujita, H.; Esposito, M. Assessing BERT’s ability to learn Italian syntax: A study on null-subject and agreement phenomena. J. Ambient. Intell. Humaniz. Comput. Volume 12 2021, 30, 1–15.
- Chi, E.A.; Hewitt, J.; Manning, C.D. Finding universal grammatical relations in multilingual BERT. arXiv 2020, arXiv:2005.04511.
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language Models are Few-Shot Learners. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–12 December 2020; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M., Lin, H., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 1877–1901.
- Floridi, L.; Chiriatti, M. GPT-3: Its nature, scope, limits, and consequences. Minds Mach. 2020, 30, 681–694.
- Jawahar, G.; Sagot, B.; Seddah, D. What does BERT learn about the structure of language? In Proceedings of the ACL 2019-57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019.
- Liu, X.; Zheng, Y.; Du, Z.; Ding, M.; Qian, Y.; Yang, Z.; Tang, J. GPT understands, too. arXiv 2021, arXiv:2103.10385.
- Rogers, A.; Kovaleva, O.; Rumshisky, A. A primer in bertology: What we know about how bert works. Trans. Assoc. Comput. Linguist. 2020, 8, 842–866.
- Jiang, Z.; Xu, F.F.; Araki, J.; Neubig, G. How can we know what language models know? Trans. Assoc. Comput. Linguist. 2020, 8, 423–438.
- Nielsen, M.A.; Chuang, I. Quantum computation and quantum information. Am. J. Phys. 2002, 70, 558.
- Kazem, B.R.; Saleh, M.B. The Effect of Pauli gates on the superposition for four-qubit in Bloch sphere. J. Kerbala Univ. 2020, 18, 33–46.
- Ben-David, S.; Childs, A.M.; Gilyén, A.; Kretschmer, W.; Podder, S.; Wang, D. Symmetries, graph properties, and quantum speedups. In Proceedings of the 2020 IEEE 61st Annual Symposium on Foundations of Computer Science (FOCS), Durham, NC, USA, 16–19 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 649–660.
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum machine learning. Nature 2017, 549, 195–202.
- Coecke, B. Kindergarten quantum mechanics: Lecture notes. Aip Conf. Proc. 2006, 810, 81–98.
- Coecke, B.; Kissinger, A. Picturing quantum processes. In Proceedings of the International Conference on Theory and Application of Diagrams, Edinburgh, UK, 18–22 June 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 28–31.
- Harris, Z.S. Distributional structure. Word 1954, 10, 146–162.
- Steedman, M.; Baldridge, J. Combinatory categorial grammar. In Non-Transformational Syntax: Formal and Explicit Models of Grammar; Wiley-Blackwell: Hoboken, NJ, USA, 2011; pp. 181–224.
- Buhrmester, V.; Münch, D.; Arens, M. Analysis of explainers of black box deep neural networks for computer vision: A survey. Mach. Learn. Knowl. Extr. 2021, 3, 966–989.
- Montague, R. Universal grammar. In Formal Philosophy; Yale University Press: London, UK, 1974; Volume 1970, pp. 222–246.
- Ajdukiewicz, K. Die syntaktische Konnexit ät. Stud. Philos. 1935, 1, 1–27.
- Bar-Hillel, Y. A quasi-arithmetical notation for syntactic description. Language 1953, 29, 47–58.
- Lambek, J. The mathematics of sentence structure. Am. Math. Mon. 1958, 65, 154–170.
- Lambek, J. Type grammar revisited. In Proceedings of the International Conference on Logical Aspects of Computational Linguistics, Nancy, France, 22–24 September 1997; Springer: Berlin/Heidelberg, Germany, 1997; pp. 1–27.
- Clark, S.; Coecke, B.; Sadrzadeh, M. A compositional distributional model of meaning. In Proceedings of the Second Quantum Interaction Symposium (QI-2008), Oxford, UK, 26–28 March 2008; pp. 133–140.
- Coecke, B.; Sadrzadeh, M.; Clark, S. Mathematical foundations for a compositional distributional model of meaning. arXiv 2010, arXiv:1003.4394.
- Buszkowski, W. Lambek grammars based on pregroups. In Proceedings of the International Conference on Logical Aspects of Computational Linguistics, Le Croisic, France, 27–29 June 2001; Springer: Berlin/Heidelberg, Germany, 2001; pp. 95–109.
- Coecke, B.; de Felice, G.; Meichanetzidis, K.; Toumi, A.; Gogioso, S.; Chiappori, N. Quantum Natural Language Processing. 2020. Available online: http://www.cs.ox.ac.uk/people/bob.coecke/QNLP-ACT.pdf (accessed on 1 June 2022).
- Coecke, B.; de Felice, G.; Meichanetzidis, K.; Toumi, A. Foundations for Near-Term Quantum Natural Language Processing. arXiv 2020, arXiv:2012.03755.
- Abramsky, S.; Coecke, B. Categorical quantum mechanics. Handb. Quantum Log. Quantum Struct. 2009, 2, 261–325.
- Meichanetzidis, K.; Gogioso, S.; de Felice, G.; Chiappori, N.; Toumi, A.; Coecke, B. Quantum Natural Language Processing on Near-Term Quantum Computers. Electron. Proc. Theor. Comput. Sci. 2021, 340, 213–229.
- Sordoni, A.; Nie, J.Y.; Bengio, Y. Modeling term dependencies with quantum language models for ir. In Proceedings of the 36th International ACM SIGIR Conference on Research and Development in Information Retrieval, Dublin, Ireland, 28 July–1 August 2013; pp. 653–662.
- Li, Q.; Melucci, M.; Tiwari, P. Quantum language model-based query expansion. In Proceedings of the 2018 ACM SIGIR International Conference on Theory of Information Retrieval, Tianjin, China, 14–17 September 2018; pp. 183–186.
- Jiang, Y.; Zhang, P.; Gao, H.; Song, D. A quantum interference inspired neural matching model for ad-hoc retrieval. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual, 25–30 July 2020; pp. 19–28.
- Zhang, P.; Niu, J.; Su, Z.; Wang, B.; Ma, L.; Song, D. End-to-end quantum-like language models with application to question answering. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32.
- Zhang, P.; Su, Z.; Zhang, L.; Wang, B.; Song, D. A quantum many-body wave function inspired language modeling approach. In Proceedings of the 27th ACM International Conference on Information and Knowledge Management, Torino, Italy, 22–26 October 2018; pp. 1303–1312.
- Li, Q.; Wang, B.; Melucci, M. CNM: An Interpretable Complex-valued Network for Matching. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), Minneapolis, MN, USA, 2–7 June 2019; Association for Computational Linguistics: Minneapolis, MN, USA, 2019; pp. 4139–4148.
- Zhang, Y.; Song, D.; Li, X.; Zhang, P. Unsupervised sentiment analysis of twitter posts using density matrix representation. In Proceedings of the European Conference on Information Retrieval, Grenoble, France, 26–29 March 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 316–329.
- Zhang, Y.; Li, Q.; Song, D.; Zhang, P.; Wang, P. Quantum-Inspired Interactive Networks for Conversational Sentiment Analysis. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI-19, Macao, China, 10–16 August 2019; pp. 5436–5442.
- Zhang, P.; Zhang, J.; Ma, X.; Rao, S.; Tian, G.; Wang, J. TextTN: Probabilistic Encoding of Language on Tensor Network. In Proceedings of the International Conference on Learning Representations, Vienna, Austria, 4 May 2021.
- Meichanetzidis, K.; Toumi, A.; de Felice, G.; Coecke, B. Grammar-Aware Question-Answering on Quantum Computers. arXiv 2020, arXiv:2012.03756.
- Benedetti, M.; Lloyd, E.; Sack, S.; Fiorentini, M. Parameterized quantum circuits as machine learning models. Quantum Sci. Technol. 2019, 4, 043001.
- Baez, J.; Stay, M. Physics, topology, logic and computation: A Rosetta Stone. In New Structures for Physics; Springer: Berlin/Heidelberg, Germany, 2010; pp. 95–172.
- Selinger, P. A survey of graphical languages for monoidal categories. In New Structures for Physics; Springer: Berlin/Heidelberg, Germany, 2010; pp. 289–355.
- Chomsky, N. Three models for the description of language. IRE Trans. Inf. Theory 1956, 2, 113–124.
- Lorenz, R.; Pearson, A.; Meichanetzidis, K.; Kartsaklis, D.; Coecke, B. Qnlp in practice: Running compositional models of meaning on a quantum computer. arXiv 2021, arXiv:2102.12846.
- Rimell, L.; Maillard, J.; Polajnar, T.; Clark, S. RELPRON: A relative clause evaluation data set for compositional distributional semantics. Comput. Linguist. 2016, 42, 661–701.
- Vicente Nieto, I. Towards Machine Translation with Quantum Computers. Master’s Thesis, University of Stockholm, Stockholm, Sweden, 2021.




