Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Zezhao Wen
 -- 3766 2022-05-31 14:30:15 |
2 format
Jason Zhu
 -69 word(s) 3697 2022-06-01 03:40:00 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Wen, Z.; Zhang, H.; Mueller, M. High Temperature Superconducting Flux Pumps for Contactless Energization. Encyclopedia. Available online: https://encyclopedia.pub/entry/23605 (accessed on 27 September 2024).
Wen Z, Zhang H, Mueller M. High Temperature Superconducting Flux Pumps for Contactless Energization. Encyclopedia. Available at: https://encyclopedia.pub/entry/23605. Accessed September 27, 2024.
Wen, Zezhao, Hongye Zhang, Markus Mueller. "High Temperature Superconducting Flux Pumps for Contactless Energization" Encyclopedia, https://encyclopedia.pub/entry/23605 (accessed September 27, 2024).
Wen, Z., Zhang, H., & Mueller, M. (2022, May 31). High Temperature Superconducting Flux Pumps for Contactless Energization. In Encyclopedia. https://encyclopedia.pub/entry/23605
Wen, Zezhao, et al. "High Temperature Superconducting Flux Pumps for Contactless Energization." Encyclopedia. Web. 31 May, 2022.
High Temperature Superconducting Flux Pumps for Contactless Energization
Edit
This entry is adapted from the peer-reviewed paper 10.3390/cryst12060766

The development of superconducting technology has seen continuously increasing interest, especially in the area of clean power systems and electrification of transport with low CO2 emission. Electric machines, as the major producer and consumer of the global electrical energy, have played a critical role in achieving zero carbon emission. The superior current carrying capacity of superconductors with zero DC loss opens the way to the next-generation electric machines characterized by much higher efficiency and power density compared to conventional machines. The persistent current mode is the optimal working condition for a superconducting magnet, and thus the energization of superconducting field windings has become a crucial challenge to be tackled, to which high temperature superconducting (HTS) flux pumps have been proposed as a promising solution. An HTS flux pump enables current injection into a closed superconducting coil wirelessly and provides continuous compensation to offset current decay, avoiding excessive cryogenic losses and sophisticated power electronics facilities.

high temperature superconductor flux pump superconducting magnet

1. Introduction

The maturation of superconducting technology has led to a wide range of industrial applications and commercial products. Magnetic resonance imagining (MRI) and nuclear magnetic resonance (NMR) machines are vital equipment in modern medical diagnosis, which usually employ superconducting magnets to provide the required magnetic fields for physical examination of states of matter [1][2]. In the domain of motors/generators [3][4][5][6][7][8][9][10], superconductors have been attracting more and more attention since they are believed to be the optimal choice for electrification of large-size transport, such as electric aircraft, which requires the power density to be as high as possible. In the conceptual design of a hybrid-electric short-range aircraft A320 proposed by Rolls Royce and Siemens [11], a 10 MW, 7000 rpm superconducting generator employs high temperature superconducting (HTS) coils as the field winding and Litz wires for a two-layer distributed armature winding, which is capable of achieving a power density greater than 20 kW/kg. Another exemplary superconducting hybrid-aircraft project, funded by the German government, adapts the radial-flux-type fully superconducting electric motors and generators [12].
All the significant applications mentioned above rely on the superconductors to provide strong magnetic fields in an efficient way. It has been widely demonstrated that ultra-high magnetic fields can be obtained utilizing superconductors via various approaches [13][14][15][16][17][18]. Superconductor bulks have been fabricated to achieve a magnetic field of 17.24 T at 29 K using Y-Ba-Cu-O (YBCO) [19] and 17.6 T at 26 K [20], and [21] reported a trapped field of 17.7 T in a stack of superconductor tapes, all of which are an order of intensity stronger than a permanent magnet. However, the cost required for the corresponding cooling and charging system is extremely expensive and in some cases even unaffordable [22]. Advances made in the manufacture of coated conductors (CCs) [23][24][25], has enabled the production of long length superconducting CCs with robust bending tolerance suitable for winding superconductor coils. Compared to bulks and tape stacks, CC coils have much better mechanical properties [26] and flexibility in terms of demagnetization and ease of maintenance [27]. These benefits make superconducting CC coils a competitive candidate for high magnetic field usage, and thus lead to a critical question: how should superconducting coils be energized?
Technically, there are only two options for energizing a coil, namely direct injection and indirect induction. By the means of direct injection, coils are connected to a power supply and energized through current leads [28]. This straightforward approach can be excruciating when the current is especially high because the current leads for transmitting very high current are extraordinarily bulky, such as that in W7-X, where 17.6 kA is required [29]. Moreover, the multistage cooling used in a Large Hardon Collier (LHC) machine dictates the current while making the current leads more tortuous [30]. More importantly, the current leads physically bridge the cryostat with ambident environment at room temperatures, imposing heavy thermal loads for the cooling system [31][32][33] and resulting in substantial additional capital and operating costs [34]. This becomes a particularly severe problem for HTS coils, for which it is challenging to self-maintain a persistent current mode due to flux creep [35], so that the current leads need to be permanently placed during the operation. In order to tackle this problem, HTS flux pumps, which can constantly drive magnetic flux into a closed superconducting loop without physical connections, have been proposed, serving as an ideal alternative to direct injection.

2. Travelling Wave HTS Flux Pumps

Inspired by the experimental tests in [36], it has been widely demonstrated that HTS flux pumps can be achieved by employing travelling magnetic waves. The generalized schematic diagram for a travelling wave HTS flux pump is illustrated, which can be modeled by the equivalent circuit. When an alternating magnetic field travels across the surface of HTSCs (typically HTS tapes), eddy currents will be induced and circulated within the superconductor. The current then results in an electric field, whose time-averaged integration over one cycle is derived to be a non-zero value. If the HTS tapes are connected to a load (usually HTS coils) to from a closed loop, then the flux pump can be considered as a DC voltage source Voc, with internal resistance of RV, charging an inductive load that has an inductance of L and resistance of RL through resistive joints RJ. The whole system can be described by a Kirchhoff voltage equation:
Under zero-state response, the pumped current I can be calculated as:
where Is is the steady state current, i.e., the maximum pumped current, Is is the time constant that is determined using the following equation:
The most important step in operating a travelling wave HTS flux pump is to provide proper alternating magnetic fields, for which effective DC voltage can be induced. According to the ways in which the magnetic fields are provided, travelling wave flux pumps can be classified to rotary HTS flux pumps and linear HTS flux pumps.

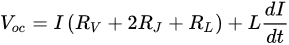
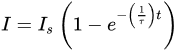
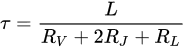
2.1. Rotary HTS Flux Pumps

HTS rotary flux pumps, or so-called HTS dynamos, firstly proposed by Hoffman et al. [37], employ one or multiple permanent magnets (PMs) mounted on a rotating disc. The rotation of disc causes spatially varying magnetic fields and forms the travelling wave required by the flux pumps.
This type of HTS flux pump has been extensively investigated, because of its simple structure and ease of operation. The basic design considerations for an HTS dynamo are the generated voltage and pumped current [38]. From Equation, the pumped current is directly determined by the effective DC voltage induced in the HTS tapes. Abundant work has been conducted to characterize the open circuit voltage for HTS dynamos, mainly credited to the research groups of the Robinson Research Institute, Victoria University of Wellington [39][40][41][42]. Inspired by the basic configuration of HTS dynamo, experiments were performed to investigate the impact of the flux gap [43], frequency (disc rotating speed) [44], tape width [45], and geometry of magnets [46] upon the open circuit voltage Voc. Generally, it has been demonstrated that Voc increases with the frequency and tape width but decreases with the flux gap. In terms of the magnet geometry, it was concluded in [46] that the generated voltage is insensitive to the orientation of the magnet but can be influenced by the magnet cross-section area. More precisely, the generated voltage shows a linear rise versus the frequency until a turning point usually appears around hundreds of Hz. After this turning frequency, nonlinear variation in the output voltage occurs, i.e., the slope of the voltage–frequency curve begins to decrease with frequency. This experimental observation was rather overlooked and not well explained until Zhang et al. [47][48] proposed and demonstrated the use of a multilayer model to investigate the electromagnetic losses in HTS-coated conductors over a wide range of frequencies. It was found in [47][48] that at frequencies higher than 100 Hz in the case of magnetization, the skin effect plays a dominant role in the determination of current distribution in an HTS CC, which results in the current drifting from the HTS layer to other non-superconducting layers, e.g., the copper stabilizers. Hence, the electric field established by the superconducting current is weakened, and thus the generated voltage experiences a progressive decrease with increasing frequencies. It is worthwhile mentioning that this is also the reason for which numerical models that only consider the HTS layer cannot manifest the nonlinear frequency response but predict a constant linear rate of increase in voltage. The generated voltage is consistently inversely proportional to the flux gap because the magnetic field experienced by the HTS tape is inversely proportional to the flux gap.
In contrast to the monotonic relationships described above, the generated voltage varies parabolically with HTS tape width in [49], namely the voltage initially increases up to a certain point and then starts to decrease as the tape width increases, which means there exists an optimal value for the tape width in order to achieve the highest voltage. However, it was found in [50] that the voltage will saturate at a certain point, after which further increase in the tape width has little impact on the voltage. The different relationships are attributed to whether or not a constant flux gap is maintained when the magnet passes over the HTS tape. The HTS dynamo modeled in [49] adopts the radial flux geometry, where the HTS tape and PM surface are flat so that the distance (along the magnetization direction) between the magnet and the tape varies as the magnet rotates. As a comparison, the model in [50] still adopts the radial flux geometry but the surface of magnet and HTS tape are curved, which will result in a constant air gap (along the magnetization direction) between the magnet and HTS tape. The underlying physics causing this peculiar bilateral tape width effect have not been reported yet, which requires further investigation. Regarding the configuration of HTS dynamos, it should be noted that a constant flux gap can also be achieved by adopting the axial flux geometry, in which the magnet is rotating in a plane parallel to the HTS tape surface.

2.2. Linear HTS Flux Pumps

A travelling wave HTS flux pump utilizes static electromagnets rather than rotating PMs to provide the alternating magnetic fields required for generating effective DC voltage in HTS tapes. The whole device resembles the structure of a linear motor and is named as a linear HTS flux pump.
The linear HTS flux pump is operated by successively exciting each set of copper coils, forming a modulated field fluctuation in space that is analogue to a travelling wave. Experiments have demonstrated [51] that the pumping performance can be influenced by the frequency, amplitude, and waveform shape of the excitation current. Basically, the flux pumping is an accumulation process, where the current in the load coils is subsequently pumped up in each operation cycle. The limits are principally determined by the critical current Ic
of the HTS tape rather than the magnetic field. Linear HTS flux pumps were observed to pump more or less the same current when operated at different frequencies and amplitudes, although a higher frequency and/or amplitude resulted in faster charging. For the waveform profiles, a triangular wave was demonstrated to be more effective than trapezoidal and sinusoidal waves. Researchers of [52] found that a standing waveform, e.g., by exciting only one of the copper coils, can also energize the HTS load coils, which was thought to be an anomalous exception, as no travelling waves are present. In fact, this phenomenon can be explained if one considers the origin of the voltage generation in the HTS tapes.

2.3. Underlying Physics

The travelling wave flux pump is a phenomenological subject, for which the underlying physics have been mysterious for years. Consider the flux pumping part, it is topologically identical to an AC alternator, where only AC voltage is supposed to be induced under AC fields without DC components. In 2014 [53], seven years later after the discovery of HTS flux pumping effects under travelling wave, Coombs et al. firstly gave a clue that the crucial difference between HTS travelling wave flux pumps and conventional AC alternators is likely to relate to the non-linear E-J characteristics, though no exhaustive explanation was given then. The first dedicated work that attempts to clarify the origin of the voltage observed in an HTS travelling wave flux pump was published by Geng et al. in 2016 [54]. They developed theoretical analysis based on a simple circuit, that is intuitively identical to the arrangement of a linear HTS flux pump, where superconducting loops can be formed by two adjacent HTS tapes.

2.4. Modeling Techniques

Various formulations have been successfully implemented into commercial software, e.g., COMSOL Multiphysics, for HTS flux pump modeling. Generally, the electromagnetic behaviors involved in operating a travelling wave HTS flux pump can be well described by Maxwell equations. Depending on the state variables selected for solving Maxwell equations, different formulations can be utilized, such as the H formulation [55][56][57][58][59], coupled H-A formulation [60][61], and coupled T-A formulation [62][63][64][65][66]. In addition, extra techniques have been developed to simplify the solution of Maxwell equations in specific aspects, including the H-formulation with shell current [50][67][68], segregated H-formulation [69][70], minimum electromagnetic entropy production (MEMEP) [71][72], integral equation (IE) [73][74][75], volume integral equation-based equivalent circuit (VIE) [76][77][78], and Chebyshev polynomials based methods [79][80][81]. Exhaustive details for each formulation can be found in the benchmark paper [82] published by Ainslie et al., which is strongly recommended to readers for acquiring information about HTS dynamo modeling. In addition, two remarks should be supplemented. The first one is, all models in [82] follow a classical assumption that the critical current of the HTS tape is constant. However, the critical current is sensitive to the magnetic field experienced by the HTS tapes, which has been shown to have significant impacts on the generated voltage [67]. Fortunately, in terms of numerical modeling, one can easily include this feature by importing the experimentally measured critical current under different fields to the model. Alternatively, one can describe the field dependence of critical current by an empirical function:
where Bpara and Bperp represent the parallel and perpendicular components of the magnetic flux density with respect to the wide face of superconducting tape. Jc0, B0, k, and α are constant coefficients related to materials. It also should be pointed out that the models in [82] only consider the superconducting layer of an HTS tape. This approximation is valid only under low frequencies, because for relative higher frequencies (hundreds of Hz or above) the currents induced by external magnetic fields tend to be drawn away from the HTS layer to its edges due to the skin effect, which cannot be reflected by a single layer model [83]. Therefore, it is necessary to consider all layers in a coated HTS conductor, e.g., the copper stabilizers, silver overlayer as well as substrate. With the two remarks added, one should obtain a numerical model that possess the full capability to simulate the behavior of a travelling wave HTS flux pump. Up to now, most of the modeling techniques are mainly implemented for a rotary HTS flux pump, due to its structural simplicity. The rotary HTS flux pump and linear HTS flux pump share exactly the same physical mechanism. The modeling techniques for HTS dynamos modeling can be confidently transferred to model HTS flux pumps, while the only difference lies in modeling the applied field either by a remanent flux density (for PMs) or an excitation current (for electromagnets).
In addition to the widely used 2D models, Asef et al. [84] proposed the first 3D model for an HTS dynamo, based on the MEMEP approach that they initially proposed for 2D HTS dynamo modeling. This model has shown good agreement with experiments as well as the 2D models. The highlight of this model is that it visualizes the screening current and electric field distribution across the HTS tape surface, which is significant as it provides evidence for the mechanism explanation based on the eddy current circulation. So far, the models discussed above usually only cover the flux pumping part aiming to investigate the open circuit voltage output. In order to replicate a travelling wave HTS flux pump in full, one should also include the superconducting coils under charge. Researchers of [85] modeled the full charging process for an HTS dynamo, where the load coils are simplified as a series combination of an inductor and resistor with predetermined values. To link the flux pumping part with the load coils being charged, the constraint imposed to maintain the current in HTS tapes, as previously described by Equation, should be amended accordingly:
where It denotes the currents stimulated (by the induced voltage across the HTS tapes) in the coils and hence also flowing through the HTS tapes as a complete circuit loop.

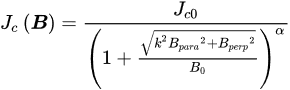
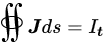
3. Transformer-Rectifier HTS Flux Pumps

An alternating current i1 is induced in the secondary winding of the transformer, which is connected to the HTS bridge and coil and forms two loops in parallel. Initially, the HTS bridge short-circuits the HTS coil, and i2 flows through loop1 only. Under certain conditions, the HTS bridge can exhibit temporary resistivity; thus, breaks the short circuit and forms a rectifier. Consequently, the HTS coil can be charged by a current iL flowing in loop2. When the HTS bridge eliminates its resistivity, the HTS coil is again short-circuited and hence flux is trapped. The flux pumping process involved here is, in essence, similar to LTS flux pumps. The difference is that the resistive region in HTSCs (analogue to the normal region in LTSCs) requires no elimination of superconductivity. Depending on how to trigger the resistivity in the HTS bridge, there are AC field switched [86][87][88][89] and self-regulating transformer-rectifier HTS flux pumps [90][91][92].

3.1. AC Field Switched Transformer-Rectifier HTS Flux Pumps

3.1.1. Topology

This type of flux pump was firstly demonstrated by Geng and Coombs [87]. When the HTS bridge carries a current i2 induced in the secondary winding, an alternating magnetic field is applied perpendicularly to the surface of the HTS bridge. As long as i2 flows in one direction in the HTS bridge with the existence of the alternating field, resistivity can be triggered.
Several influential factors on the flux pumping performance were examined in the comprehensive research presented in [86], including excitation current magnitude, applied field magnitude, frequency and duration, and phase differences between current and field. Briefly, the pumping current decreases from its maximum at no phase misalignment (the transporting current is in phase with the field) to zero at 90 degrees phase difference; an increase in either the strength or frequency of the applied field leads to a continuously increasing pumped current; the duration of the applied field (i.e., how long the resistivity in the HTS bridge is maintained) has negligible impact on the pumping current. The influence of the excitation current is relatively more complicated: the pumping current increases with the excitation current magnitude up to a turning point, after which it starts to drop if the excitation current increases further, implying that there exists an optimal excitation current to maximize the pumping current. In addition, it was found in [93] that adding an actual resistance to the secondary winding can enhance the pumping current, especially when the desired current is high.

3.1.2. Mechanism

The working principle of an AC field switched transformer-rectifier HTS flux pump is crystal clear, since it is completely based on the well described dynamic resistance effect [94][95][96]. It is known that the external magnetic field Bext penetrates certain distance into the superconductor from its edges. The penetration depth increases with the magnetic field.

3.2. Self-Regulating Transformer-Rectifier HTS Flux Pumps

3.2.1. Topology

Geng et al. [97] further developed the self-regulating transformer-rectifier HTS flux pump, which are hand-in-hand with the AC field switched ones. The two prototypes share almost the same topology, whilst the only difference is whether the field generating component is included. In a self-regulating transformer-rectifier HTS flux pump, the AC magnetic field is no longer required to trigger resistivity in the HTS bridge. Alternatively, a highly asymmetric (the absolute value of positive peak is much higher than its negative peak) current is injected into the primary winding. Then, resistivity can be trigged for the HTS bridge when it conducts the positive peak current. With this approach, it eliminates the troublesome field modulation, making the whole operation solely driven by current. As a result, the operational considerations are less than that for an AC field switched HTS flux pump, principally only the magnitude and frequency of the primary current. As experimentally demonstrated in [97], unlike the AC field switched ones, where the primary current magnitude has a bilateral effect, the pumping current for a self-regulating flux pump continuously increases with the primary current. More or less the same pumping current was obtained for various primary current frequencies, but faster charging speed was observed under higher frequencies.

3.2.2. Mechanism

Intuitively, due to the topological similarity, the mechanism of self-regulating flux pumps is close to the AC field switched ones, but slightly different. For type II superconductors, the current and electric field relations normally can be described by the exponential E-J power law as Equation. Visualizing this equation one can find that if the current density exceeds a threshold value, the superconductor will enter the flux flow regime and exhibit obvious resistivity. Thus, if some parts of the secondary current waveform (e.g., the positive peak region) are greater while all the rest are smaller than the threshold, the HTS bridge can possess temporary resistivity in one cycle and hence provides the rectification effect. This is the reason why the primary current must be highly asymmetric, and the flux pump can only operate in half-wave mode.

3.3. Modeling Techniques

Most previous work about transformer-rectifier HTS flux pumps are experimental, a good example of the modeling can be found in [98]. The transformer can be equivalently substituted by a magnetic field applied perpendicularly to loop1, which can induce a circulating screen current, accordingly. The whole system then can be simplified to three parallel HTS tapes connected at the terminals, which is reflected by a global constraint equation:
Later, a novel modeling approach was proposed in [99]. Different from those formulation-based models aiming to solve Maxwell equations, this model completely relies on the circuit analysis. By combining Equations, one can express the net output voltage across the HTS bridge as:
 which can then be utilized to calculate the current in an inductive coil with fixed inductance, similar to Equation. This method evades sophisticated electromagnetic interactions that occur in the real operation by applying a set of approximated equations, so it is much more efficient than finite element methods (FEM), in terms of solution time.

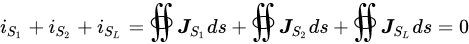
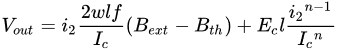
References

  1. Weijers, H.; Trociewitz, U.; Markiewicz, W.; Jiang, J.; Myers, D.; Hellstrom, E.; Xu, A.; Jaroszynski, J.; Noyes, P.; Viouchkov, Y. High field magnets with HTS conductors. IEEE Trans. Appl. Supercond. 2010, 20, 576–582.
  2. Hahn, S.; Park, D.K.; Voccio, J.; Bascunan, J.; Iwasa, Y. No-Insulation (NI) HTS Inserts for > 1 GHz LTS/HTS NMR Magnets. IEEE Trans. Appl. Supercond. 2011, 22, 4302405.
  3. Abrahamsen, A.B.; Mijatovic, N.; Seiler, E.; Zirngibl, T.; Træholt, C.; Nørgård, P.B.; Pedersen, N.F.; Andersen, N.H.; Østergaard, J. Superconducting wind turbine generators. Supercond. Sci. Technol. 2010, 23, 034019.
  4. Sivasubramaniam, K.; Zhang, T.; Lokhandwalla, M.; Laskaris, E.; Bray, J.; Gerstler, B.; Shah, M.; Alexander, J. Development of a high speed HTS generator for airborne applications. IEEE Trans. Appl. Supercond. 2009, 19, 1656–1661.
  5. Miki, M.; Tokura, S.; Hayakawa, H.; Inami, H.; Kitano, M.; Matsuzaki, H.; Kimura, Y.; Ohtani, I.; Morita, E.; Ogata, H. Development of a synchronous motor with Gd–Ba–Cu–O bulk superconductors as pole-field magnets for propulsion system. Supercond. Sci. Technol. 2006, 19, S494.
  6. Umemoto, K.; Aizawa, K.; Yokoyama, M.; Yoshikawa, K.; Kimura, Y.; Izumi, M.; Ohashi, K.; Numano, M.; Okumura, K.; Yamaguchi, M. Development of 1 MW-class HTS motor for podded ship propulsion system. J. Phys. Conf. Ser. 2010, 234, 032060.
  7. Nick, W.; Frank, M.; Klaus, G.; Frauenhofer, J.; Neumuller, H.-W. Operational experience with the world’s first 3600 rpm 4 MVA generator at Siemens. IEEE Trans. Appl. Supercond. 2007, 17, 2030–2033.
  8. Sung, H.-J.; Kim, G.-H.; Kim, K.; Jung, S.-J.; Park, M.; Yu, I.-K.; Kim, Y.-G.; Lee, H.; Kim, A.-R. Practical design of a 10 MW superconducting wind power generator considering weight issue. IEEE Trans. Appl. Supercond. 2013, 23, 5201805.
  9. Karmaker, H.; Ho, M.; Chen, E.; Kulkarni, D. Direct drive HTS wind generator design for commercial applications. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 491–495.
  10. Sung, H.-J.; Kim, G.-H.; Kim, K.; Park, M.; Yu, I.-K.; Kim, J.-Y. Design and comparative analysis of 10 MW class superconducting wind power generators according to different types of superconducting wires. Phys. C Supercond. 2013, 494, 255–261.
  11. Filipenko, M.; Kühn, L.; Gleixner, T.; Thummet, M.; Lessmann, M.; Möller, D.; Böhm, M.; Schröter, A.; Häse, K.; Grundmann, J. Concept design of a high power superconducting generator for future hybrid-electric aircraft. Supercond. Sci. Technol. 2020, 33, 054002.
  12. Boll, M.; Corduan, M.; Biser, S.; Filipenko, M.; Pham, Q.H.; Schlachter, S.; Rostek, P.; Noe, M. A holistic system approach for short range passenger aircraft with cryogenic propulsion system. Supercond. Sci. Technol. 2020, 33, 044014.
  13. Lvovsky, Y.; Stautner, E.W.; Zhang, T. Novel technologies and configurations of superconducting magnets for MRI. Supercond. Sci. Technol. 2013, 26, 093001.
  14. Corato, V.; Bagni, T.; Biancolini, M.; Bonifetto, R.; Bruzzone, P.; Bykovsky, N.; Ciazynski, D.; Coleman, M.; Della Corte, A.; Dembkowska, A. Progress in the design of the superconducting magnets for the EU DEMO. Fusion Eng. Des. 2018, 136, 1597–1604.
  15. Zhang, M.; Yuan, W.; Hilton, D.K.; Canassy, M.D.; Trociewitz, U.P. Study of second-generation high-temperature superconducting magnets: The self-field screening effect. Supercond. Sci. Technol. 2014, 27, 095010.
  16. Khodzhibagiyan, H.; Agapov, N.; Akishin, P.; Blinov, N.; Borisov, V.; Bychkov, A.; Galimov, A.; Donyagin, A.; Karpinskiy, V.; Korolev, V. Superconducting magnets for the NICA accelerator collider complex. IEEE Trans. Appl. Supercond. 2013, 24, 4001304.
  17. Rossi, L. Superconducting magnets for the LHC main lattice. IEEE Trans. Appl. Supercond. 2004, 14, 153–158.
  18. Yokoyama, K.; Oka, T.; Okada, H.; Fujine, Y.; Chiba, A.; Noto, K. Solid-liquid magnetic separation using bulk superconducting magnets. IEEE Trans. Appl. Supercond. 2003, 13, 1592–1595.
  19. Tomita, M.; Murakami, M. High-temperature superconductor bulk magnets that can trap magnetic fields of over 17 tesla at 29 K. Nature 2003, 421, 517–520.
  20. Durrell, J.H.; Dennis, A.R.; Jaroszynski, J.; Ainslie, M.D.; Palmer, K.G.; Shi, Y.; Campbell, A.M.; Hull, J.; Strasik, M.; Hellstrom, E. A trapped field of 17.6 T in melt-processed, bulk Gd-Ba-Cu-O reinforced with shrink-fit steel. Supercond. Sci. Technol. 2014, 27, 082001.
  21. Patel, A.; Baskys, A.; Mitchell-Williams, T.; McCaul, A.; Coniglio, W.; Hänisch, J.; Lao, M.; Glowacki, B.A. A trapped field of 17.7 T in a stack of high temperature superconducting tape. Supercond. Sci. Technol. 2018, 31, 09LT01.
  22. Toth, J.; Bole, S. Design, construction, and first testing of a 41.5 T all-resistive magnet at the NHMFL in Tallahassee. IEEE Trans. Appl. Supercond. 2017, 28, 4300104.
  23. Iijima, Y.; Kaneko, N.; Hanyu, S.; Sutoh, Y.; Kakimoto, K.; Ajimura, S.; Saitoh, T. Development of IBAD/PLD process for long length Y-123 conductors in Fujikura. Phys. C Supercond. Appl. 2006, 445, 509–514.
  24. Freyhardt, H.C. YBaCuO and REBaCuO HTS for applications. Int. J. Appl. Ceram. Technol. 2007, 4, 203–216.
  25. Shiohara, Y.; Yoshizumi, M.; Izumi, T.; Yamada, Y. Present status and future prospect of coated conductor development and its application in Japan. Supercond. Sci. Technol. 2008, 21, 034002.
  26. Sugano, M.; Osamura, K.; Prusseit, W.; Semerad, R.; Kuroda, T.; Itoh, K.; Kiyoshi, T. Reversible strain dependence of critical current in 100 A class coated conductors. IEEE Trans. Appl. Supercond. 2005, 15, 3581–3584.
  27. Lee, J.-H.; Lee, H.; Lee, J.-W.; Choi, S.-M.; Yoo, S.-I.; Moon, S.-H. RCE-DR, a novel process for coated conductor fabrication with high performance. Supercond. Sci. Technol. 2014, 27, 044018.
  28. Ballarino, A. Current leads, links and buses. arXiv 2015, arXiv:1501.07166.
  29. Wegener, L. Status of Wendelstein 7-X construction. Fusion Eng. Des. 2009, 84, 106–112.
  30. Ballarino, A. Current leads for the LHC magnet system. IEEE Trans. Appl. Supercond. 2002, 12, 1275–1280.
  31. Bumby, C.W.; Badcock, R.A.; Sung, H.-J.; Kim, K.-M.; Jiang, Z.; Pantoja, A.E.; Bernardo, P.; Park, M.; Buckley, R.G. Development of a brushless HTS exciter for a 10 kW HTS synchronous generator. Supercond. Sci. Technol. 2016, 29, 024008.
  32. Sung, H.; Badcock, R.; Jiang, Z.; Choi, J.; Park, M.; Yu, I. Design and heat load analysis of a 12 MW HTS wind power generator module employing a brushless HTS exciter. IEEE Trans. Appl. Supercond. 2016, 26, 5205404.
  33. Jeon, H.; Lee, J.; Han, S.; Kim, J.H.; Hyeon, C.J.; Kim, H.M.; Park, D.; Do Chung, Y.; Ko, T.K.; Yoon, Y.S. Methods for increasing the saturation current and charging speed of a rotary HTS flux-pump to charge the field coil of a synchronous motor. IEEE Trans. Appl. Supercond. 2018, 28, 5202605.
  34. Kalsi, S.S. Applications of High Temperature Superconductors to Electric Power Equipment; John Wiley & Sons: Hoboken, NJ, USA, 2011.
  35. Feigel’man, M.; Geshkenbein, V.; Vinokur, V. Flux creep and current relaxation in high-T c superconductors. Phys. Rev. B 1991, 43, 6263.
  36. Coombs, T.; Hong, Z.; Zhu, X. A thermally actuated superconducting flux pump. Phys. C Supercond. 2008, 468, 153–159.
  37. Hoffmann, C.; Pooke, D.; Caplin, A.D. Flux pump for HTS magnets. IEEE Trans. Appl. Supercond. 2010, 21, 1628–1631.
  38. Hoffmann, C.; Walsh, R.; Karrer-Mueller, E.; Pooke, D. Design parameters for an HTS flux pump. Phys. Procedia 2012, 36, 1324–1329.
  39. Bumby, C.W.; Pantoja, A.E.; Sung, H.-J.; Jiang, Z.; Kulkarni, R.; Badcock, R.A. Through-wall excitation of a magnet coil by an external-rotor HTS flux pump. IEEE Trans. Appl. Supercond. 2016, 26, 0500505.
  40. Storey, J.G.; Pantoja, A.E.; Jiang, Z.; Hamilton, K.; Badcock, R.A.; Bumby, C.W. Impact of annular yoke geometry on performance of a dynamo-type HTS flux pump. IEEE Trans. Appl. Supercond. 2018, 28, 5203906.
  41. Pantoja, A.E.; Storey, J.G.; Badcock, R.A.; Jiang, Z.; Phang, S.; Bumby, C.W. Output during continuous frequency ramping of a dynamo-type HTS flux pump. IEEE Trans. Appl. Supercond. 2018, 28, 5202205.
  42. Storey, J.G.; Pantoja, A.E.; Jiang, Z.; Badcock, R.A.; Bumby, C.W. Optimizing rotor speed and geometry for an externally mounted HTS dynamo. IEEE Trans. Appl. Supercond. 2019, 29, 5202705.
  43. Jiang, Z.; Bumby, C.W.; Badcock, R.A.; Sung, H.-J.; Long, N.J.; Amemiya, N. Impact of flux gap upon dynamic resistance of a rotating HTS flux pump. Supercond. Sci. Technol. 2015, 28, 115008.
  44. Bumby, C.W.; Phang, S.; Pantoja, A.E.; Jiang, Z.; Storey, J.G.; Sung, H.-J.; Park, M.; Badcock, R.A. Frequency dependent behavior of a dynamo-type HTS flux pump. IEEE Trans. Appl. Supercond. 2016, 27, 5200705.
  45. Pantoja, A.E.; Jiang, Z.; Badcock, R.A.; Bumby, C.W. Impact of stator wire width on output of a dynamo-type HTS flux pump. IEEE Trans. Appl. Supercond. 2016, 26, 4805208.
  46. Badcock, R.A.; Phang, S.; Pantoja, A.E.; Jiang, Z.; Storey, J.G.; Sung, H.-J.; Park, M.; Bumby, C.W. Impact of magnet geometry on output of a dynamo-type HTS flux pump. IEEE Trans. Appl. Supercond. 2016, 27, 5200905.
  47. Zhang, H.; Yao, M.; Kails, K.; Machura, P.; Mueller, M.; Jiang, Z.; Xin, Y.; Li, Q. Modelling of electromagnetic loss in HTS coated conductors over a wide frequency band. Supercond. Sci. Technol. 2020, 33, 025004.
  48. Zhang, H.; Chen, H.; Jiang, Z.; Yang, T.; Xin, Y.; Mueller, M.; Li, Q. A full-range formulation for dynamic loss of high-temperature superconductor coated conductors. Supercond. Sci. Technol. 2020, 33, 05LT01.
  49. Wen, Z.; Zhang, H.; Mueller, M. Sensitivity analysis and machine learning modelling for the output characteristics of rotary HTS flux pumps. Supercond. Sci. Technol. 2021, 34, 125019.
  50. Mataira, R.; Ainslie, M.D.; Badcock, R.; Bumby, C.W. Modeling of Stator Versus Magnet Width Effects in High-$ T_c $ Superconducting Dynamos. IEEE Trans. Appl. Supercond. 2020, 30, 5204406.
  51. Fu, L.; Matsuda, K.; Lecrevisse, T.; Iwasa, Y.; Coombs, T. A flux pumping method applied to the magnetization of YBCO superconducting coils: Frequency, amplitude and waveform characteristics. Supercond. Sci. Technol. 2016, 29, 04LT01.
  52. Fu, L.; Matsuda, K.; Baghdadi, M.; Coombs, T. Linear flux pump device applied to high temperature superconducting (HTS) magnets. IEEE Trans. Appl. Supercond. 2015, 25, 4603804.
  53. Coombs, T.; Fagnard, J.-F.; Matsuda, K. Magnetization of 2-G coils and artificial bulks. IEEE Trans. Appl. Supercond. 2014, 24, 8201005.
  54. Geng, J.; Matsuda, K.; Fu, L.; Fagnard, J.-F.; Zhang, H.; Zhang, X.; Shen, B.; Dong, Q.; Baghdadi, M.; Coombs, T. Origin of dc voltage in type II superconducting flux pumps: Field, field rate of change, and current density dependence of resistivity. J. Phys. D Appl. Phys. 2016, 49, 11LT01.
  55. Kajikawa, K.; Hayashi, T.; Yoshida, R.; Iwakuma, M.; Funaki, K. Numerical evaluation of AC losses in HTS wires with 2D FEM formulated by self magnetic field. IEEE Trans. Appl. Supercond. 2003, 13, 3630–3633.
  56. Hong, Z.; Campbell, A.; Coombs, T. Numerical solution of critical state in superconductivity by finite element software. Supercond. Sci. Technol. 2006, 19, 1246.
  57. Brambilla, R.; Grilli, F.; Martini, L. Development of an edge-element model for AC loss computation of high-temperature superconductors. Supercond. Sci. Technol. 2006, 20, 16.
  58. Ainslie, M.D.; Yuan, W.; Hong, Z.; Pei, R.; Flack, T.J.; Coombs, T.A. Modeling and electrical measurement of transport AC loss in HTS-based superconducting coils for electric machines. IEEE Trans. Appl. Supercond. 2010, 21, 3265–3268.
  59. Ainslie, M.D.; Flack, T.J.; Campbell, A.M. Calculating transport AC losses in stacks of high temperature superconductor coated conductors with magnetic substrates using FEM. Phys. C Supercond. 2012, 472, 50–56.
  60. Brambilla, R.; Grilli, F.; Martini, L.; Bocchi, M.; Angeli, G. A finite-element method framework for modeling rotating machines with superconducting windings. IEEE Trans. Appl. Supercond. 2018, 28, 5207511.
  61. Santos, B.M.O.; Dias, F.J.M.; Sass, F.; Sotelo, G.G.; Polasek, A.; de Andrade, R. Simulation of superconducting machine with stacks of coated conductors using hybrid ah formulation. IEEE Trans. Appl. Supercond. 2020, 30, 5207309.
  62. Liang, F.; Venuturumilli, S.; Zhang, H.; Zhang, M.; Kvitkovic, J.; Pamidi, S.; Wang, Y.; Yuan, W. A finite element model for simulating second generation high temperature superconducting coils/stacks with large number of turns. J. Appl. Phys. 2017, 122, 043903.
  63. Zhang, H.; Zhang, M.; Yuan, W. An efficient 3D finite element method model based on the T–A formulation for superconducting coated conductors. Supercond. Sci. Technol. 2016, 30, 024005.
  64. Berrospe-Juarez, E.; Zermeño, V.M.; Trillaud, F.; Grilli, F. Real-time simulation of large-scale HTS systems: Multi-scale and homogeneous models using the T–A formulation. Supercond. Sci. Technol. 2019, 32, 065003.
  65. Grilli, F.; Pardo, E.; Morandi, A.; Gömöry, F.; Solovyov, M.; Zermeño, V.M.; Brambilla, R.; Benkel, T.; Riva, N. Electromagnetic modeling of superconductors with commercial software: Possibilities with two vector potential-based formulations. IEEE Trans. Appl. Supercond. 2020, 31, 5900109.
  66. Benkel, T.; Lao, M.; Liu, Y.; Pardo, E.; Wolfstädter, S.; Reis, T.; Grilli, F. T–A-formulation to model electrical machines with HTS coated conductor coils. IEEE Trans. Appl. Supercond. 2020, 30, 5205807.
  67. Mataira, R.; Ainslie, M.; Badcock, R.; Bumby, C. Origin of the DC output voltage from a high-Tc superconducting dynamo. Appl. Phys. Lett. 2019, 114, 162601.
  68. Mataira, R.; Ainslie, M.; Pantoja, A.; Badcock, R.; Bumby, C. Mechanism of the high-T c superconducting dynamo: Models and experiment. Phys. Rev. Appl. 2020, 14, 024012.
  69. Quéval, L.; Liu, K.; Yang, W.; Zermeño, V.M.; Ma, G. Superconducting magnetic bearings simulation using an H-formulation finite element model. Supercond. Sci. Technol. 2018, 31, 084001.
  70. Ainslie, M.D.; Quéval, L.; Mataira, R.C.; Bumby, C.W. Modelling the frequency dependence of the open-circuit voltage of a high-T c superconducting dynamo. IEEE Trans. Appl. Supercond. 2021, 31, 4900407.
  71. Pardo, E.; Šouc, J.; Frolek, L. Electromagnetic modelling of superconductors with a smooth current–voltage relation: Variational principle and coils from a few turns to large magnets. Supercond. Sci. Technol. 2015, 28, 044003.
  72. Pardo, E.; Kapolka, M. 3D computation of non-linear eddy currents: Variational method and superconducting cubic bulk. J. Comput. Phys. 2017, 344, 339–363.
  73. Brambilla, R.; Grilli, F.; Martini, L.; Sirois, F. Integral equations for the current density in thin conductors and their solution by the finite-element method. Supercond. Sci. Technol. 2008, 21, 105008.
  74. Grilli, F.; Brambilla, R.; Martini, L.F.; Sirois, F.; Nguyen, D.N.; Ashworth, S.P. Current density distribution in multiple YBCO coated conductors by coupled integral equations. IEEE Trans. Appl. Supercond. 2009, 19, 2859–2862.
  75. Brambilla, R.; Grilli, F.; Nguyen, D.N.; Martini, L.; Sirois, F. AC losses in thin superconductors: The integral equation method applied to stacks and windings. Supercond. Sci. Technol. 2009, 22, 075018.
  76. Morandi, A.; Fabbri, M.; Ribani, P.L.; Dennis, A.; Durrell, J.; Shi, Y.; Cardwell, D. The measurement and modeling of the levitation force between single-grain YBCO bulk superconductors and permanent magnets. IEEE Trans. Appl. Supercond. 2018, 28, 3601310.
  77. Fabbri, M.; Forzan, M.; Lupi, S.; Morandi, A.; Ribani, P.L. Experimental and numerical analysis of DC induction heating of aluminum billets. IEEE Trans. Magn. 2009, 45, 192–200.
  78. Perini, E.; Giunchi, G.; Geri, M.; Morandi, A. Experimental and Numerical Investigation of the Levitation Force Between Bulk Permanent Magnet and MgB2 Disk. IEEE Trans. Appl. Supercond. 2009, 19, 2124–2128.
  79. Prigozhin, L.; Sokolovsky, V. Fast solution of the superconducting dynamo benchmark problem. Supercond. Sci. Technol. 2021, 34, 065006.
  80. Prigozhin, L.; Sokolovsky, V. Two-dimensional model of a high-T c superconducting dynamo. IEEE Trans. Appl. Supercond. 2021, 31, 5201107.
  81. Sokolovsky, V.; Prigozhin, L.; Kozyrev, A.B. Chebyshev spectral method for superconductivity problems. Supercond. Sci. Technol. 2020, 33, 085008.
  82. Ainslie, M.; Grilli, F.; Quéval, L.; Pardo, E.; Perez-Mendez, F.; Mataira, R.; Morandi, A.; Ghabeli, A.; Bumby, C.; Brambilla, R. A new benchmark problem for electromagnetic modelling of superconductors: The high-T c superconducting dynamo. Supercond. Sci. Technol. 2020, 33, 105009.
  83. Zhang, H.; Machura, P.; Kails, K.; Chen, H.; Mueller, M. Dynamic loss and magnetization loss of HTS coated conductors, stacks, and coils for high-speed synchronous machines. Supercond. Sci. Technol. 2020, 33, 084008.
  84. Ghabeli, A.; Pardo, E.; Kapolka, M. 3D modeling of a superconducting dynamo-type flux pump. Sci. Rep. 2021, 11, 10296.
  85. Ghabeli, A.; Ainslie, M.; Pardo, E.; Quéval, L.; Mataira, R. Modeling the charging process of a coil by an HTS dynamo-type flux pump. Supercond. Sci. Technol. 2021, 34, 084002.
  86. Geng, J.; Matsuda, K.; Fu, L.; Shen, B.; Zhang, X.; Coombs, T. Operational research on a high-Tc rectifier-type superconducting flux pump. Supercond. Sci. Technol. 2016, 29, 035015.
  87. Geng, J.; Coombs, T. Mechanism of a high-Tc superconducting flux pump: Using alternating magnetic field to trigger flux flow. Appl. Phys. Lett. 2015, 107, 142601.
  88. Geng, J.; Painter, T.; Long, P.; Gawith, J.; Yang, J.; Ma, J.; Dong, Q.; Shen, B.; Li, C.; Coombs, T. A kilo-ampere level HTS flux pump. Supercond. Sci. Technol. 2019, 32, 074004.
  89. Zhang, H.; Geng, J.; Coombs, T. Magnetizing high-Tc superconducting coated conductor stacks using a transformer–rectifier flux pumping method. Supercond. Sci. Technol. 2018, 31, 105007.
  90. Zhou, P.; Ma, G.; Deng, Y.; Nie, X.; Zhai, Y.; Liu, K.; Zhang, H.; Li, Y. A contactless self-regulating HTS flux pump. IEEE Trans. Appl. Supercond. 2020, 30, 3603006.
  91. Geng, J.; Bumby, C.W.; Badcock, R.A. Maximising the current output from a self-switching kA-class rectifier flux pump. Supercond. Sci. Technol. 2020, 33, 045005.
  92. Zhai, Y.; Zhou, P.; Li, J.; Sun, C.; Li, Y.; Xiao, L.; Deng, Y.; Ma, G. Performance Investigation of Contactless Self-Regulating HTS Flux Pump. IEEE Trans. Appl. Supercond. 2021, 31, 4603105.
  93. Li, C.; Geng, J.; Shen, B.; Ma, J.; Gawith, J.; Coombs, T.A. Investigation on the transformer-rectifier flux pump for high field magnets. IEEE Trans. Appl. Supercond. 2019, 29, 4301105.
  94. Jiang, Z.; Hamilton, K.; Amemiya, N.; Badcock, R.; Bumby, C. Dynamic resistance of a high-Tc superconducting flux pump. Appl. Phys. Lett. 2014, 105, 112601.
  95. Zhang, H.; Hao, C.; Xin, Y.; Mueller, M. Demarcation currents and corner field for dynamic resistance of HTS-coated conductors. IEEE Trans. Appl. Supercond. 2020, 30, 6601305.
  96. Oomen, M.; Rieger, J.; Leghissa, M.; ten Haken, B.; ten Kate, H.H. Dynamic resistance in a slab-like superconductor with Jc (B) dependence. Supercond. Sci. Technol. 1999, 12, 382.
  97. Geng, J.; Coombs, T. An HTS flux pump operated by directly driving a superconductor into flux flow region in the E–J curve. Supercond. Sci. Technol. 2016, 29, 095004.
  98. Geng, J.; Coombs, T.A. Modeling methodology for a HTS flux pump using a 2D H-formulation. Supercond. Sci. Technol. 2018, 31, 125015.
  99. Li, C.; Yang, J.; Shen, B.; Ma, J.; Gawith, J.; Öztürk, Y.; Geng, J.; Coombs, T.A. A HTS flux pump simulation methodology based on the electrical circuit. IEEE Trans. Appl. Supercond. 2020, 30, 4702905.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Engineering, Electrical & Electronic
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Zezhao Wen
,
Hongye Zhang
,
Markus Mueller
View Times: 447
Revisions: 2 times (View History)
Update Date: 01 Jun 2022
Table of Contents
    1000/1000
    Hot Most Recent
    ScholarVision Creations
    Feedback