Your browser does not fully support modern features. Please upgrade for a smoother experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Hiroto Tachikawa | -- | 2238 | 2022-05-27 01:16:54 | | | |
| 2 | Rita Xu | -10 word(s) | 2228 | 2022-05-27 04:03:49 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Tachikawa, H.; Iyama, T. Reactions of Graphene Nano-Flakes. Encyclopedia. Available online: https://encyclopedia.pub/entry/23459 (accessed on 07 February 2026).
Tachikawa H, Iyama T. Reactions of Graphene Nano-Flakes. Encyclopedia. Available at: https://encyclopedia.pub/entry/23459. Accessed February 07, 2026.
Tachikawa, Hiroto, Tetsuji Iyama. "Reactions of Graphene Nano-Flakes" Encyclopedia, https://encyclopedia.pub/entry/23459 (accessed February 07, 2026).
Tachikawa, H., & Iyama, T. (2022, May 27). Reactions of Graphene Nano-Flakes. In Encyclopedia. https://encyclopedia.pub/entry/23459
Tachikawa, Hiroto and Tetsuji Iyama. "Reactions of Graphene Nano-Flakes." Encyclopedia. Web. 27 May, 2022.
Copy Citation
The elucidation of the mechanism of the chemical evolution of the universe is one of the most important themes in astrophysics. Polycyclic aromatic hydrocarbons (PAHs) provide a two-dimensional reaction field in a three-dimensional interstellar space. Additionally, PAHs play an important role as a model of graphene nanoflake (GNF) in materials chemistry.
chemical evolution
graphene
reaction dynamics
hydrogen storage
H2 reversible device
molecular device
molecular design
1. Introduction
Understanding the mechanisms of the chemical evolution of the universe is one of the most important topics of recent research in astrophysics and astrochemistry [1][2][3] About 20% of the total carbon in the universe is widely distributed in space in the form of polycyclic aromatic hydrocarbons (PAHs) [4], although the actual distribution in space and structure of PAHs are still unclear [5]. PAH is thought to provide a two-dimensional reaction field in three-dimensional interstellar space [6][7][8]. The reaction probability of bimolecular collisions increases significantly with the adsorption of molecules to the surface of PAH. Therefore, understanding the interaction between PAH and molecules is important for understanding the chemical evolution of the universe.
On the other hand, in the field of materials science, PAH is used as a model compound of graphene nanoflake (GNF) [9][10][11][12]. GNF has a wide range of applications such as hydrogen storage and lithium-ion batteries. Other applications include solar cells, energy storage devices, bio-devices, thermal management and piezoelectric materials, antibacterial materials, and filtration materials. Thus, PAH and GNF play an important role in a wide range of fields.
2. Interaction of Hydrogen Atoms with GNF
Atomic and molecular hydrogen are most abundant in interstellar space [13] If atomic hydrogen is adsorbed onto a GNF surface, several reactions can take place with other small atoms and molecules, forming more complicated molecules. Hence, the interaction of GNFs with atomic hydrogen plays an important role in the initial reactions of chemical evolution in the universe. In the field of materials science, GNF is used as a model compound of graphene [14][15][16][17]. The mechanism of hydrogen addition to GNFs is introduced using the results from density functional theory (DFT) calculations.
2.1. Bonding Structure of Hydrogen Atoms to GNFs
In density functional theory (DFT) calculations of the interaction system composed of GNF and a hydrogen atom (H), H was added to the carbon atom near the center of GNF, and the geometry was optimized. The GNF and the hydrogen-added GNF are denoted as GNF(n) and H-GNF(n), respectively, where n is the number of benzene rings in the GNF. Figure 1 shows examples of the GNFs(n) (n = 19 and 37) used in the calculations. The DFT calculations were performed on GNFs consisting of 7–37 benzene rings. The basis sets are 6-31G(d) and 6-311G(d,p) [18] and the functional Coulomb-attenuating method (CAM-B3LYP) [19] is used. Atomic charges and spin densities were determined by natural population analysis (NPA) and natural bond orbital (NBO) methods.
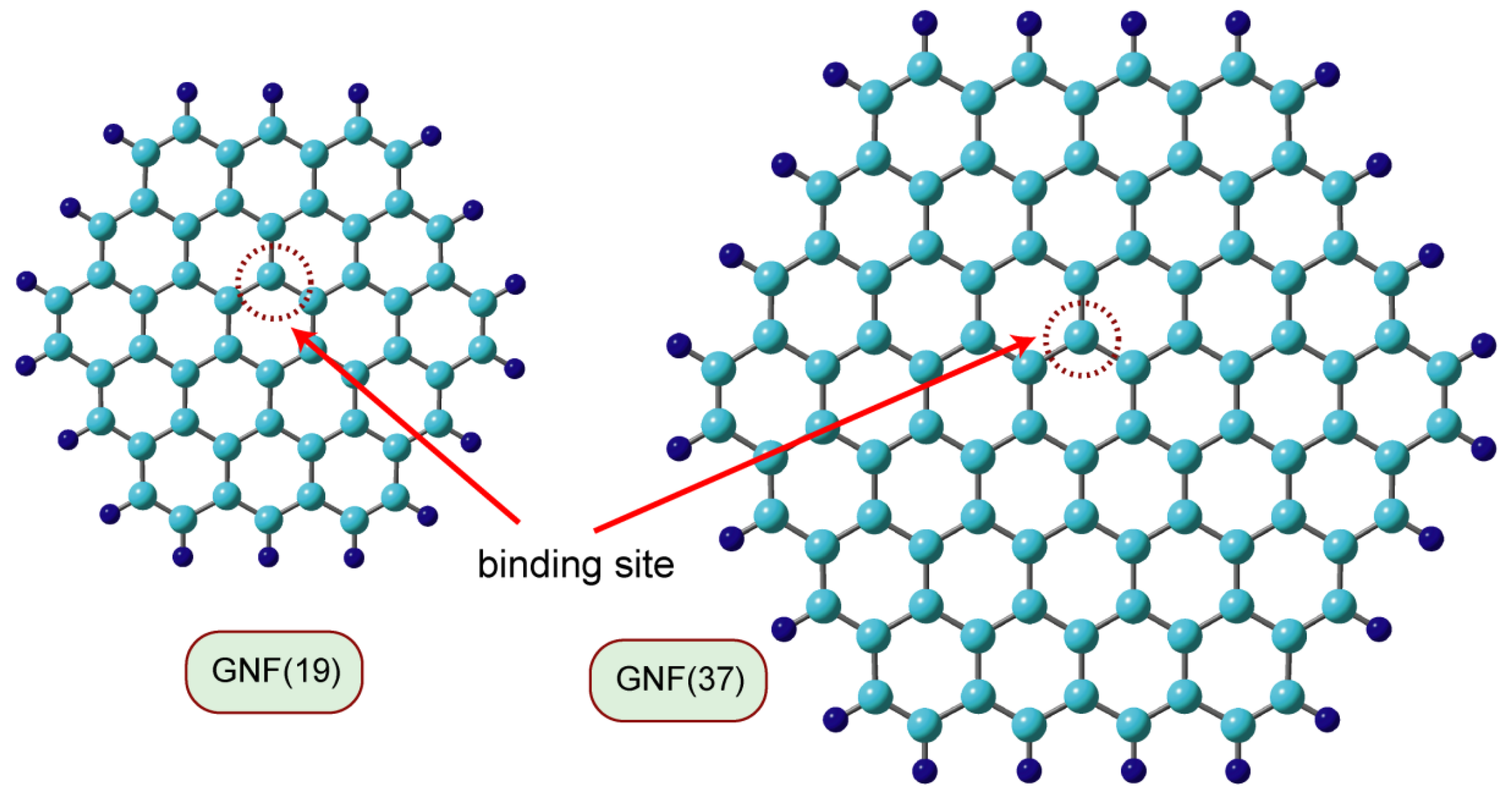
Figure 1. Models of graphene nanoflakes used in the present calculations. GNF(n) means graphene nanoflake composed of n benzene rings. GNF(19) and GNF(37) are circumcoronene (C54H18) and circumcircumcoronene (C96H24), respectively.
The optimized structure of H-GNF is shown in Figure 2. The planar structure around the H-bonded carbon atom (C0) of GNF is changed to a pyramidal one after the addition of H. The distance between the added hydrogen (H) and the bonded carbon atom (C0) is R1 = 1.114 Å. The atomic charges of C0 and H are −0.274 and +0.245, respectively, indicating that the C-H bond is locally polarized as (C0)−0.274–(H)+0.245. This suggests that the addition of H to the nonpolar GNF generates a dipole moment that facilitates the attraction of other molecules in interstellar space [20].
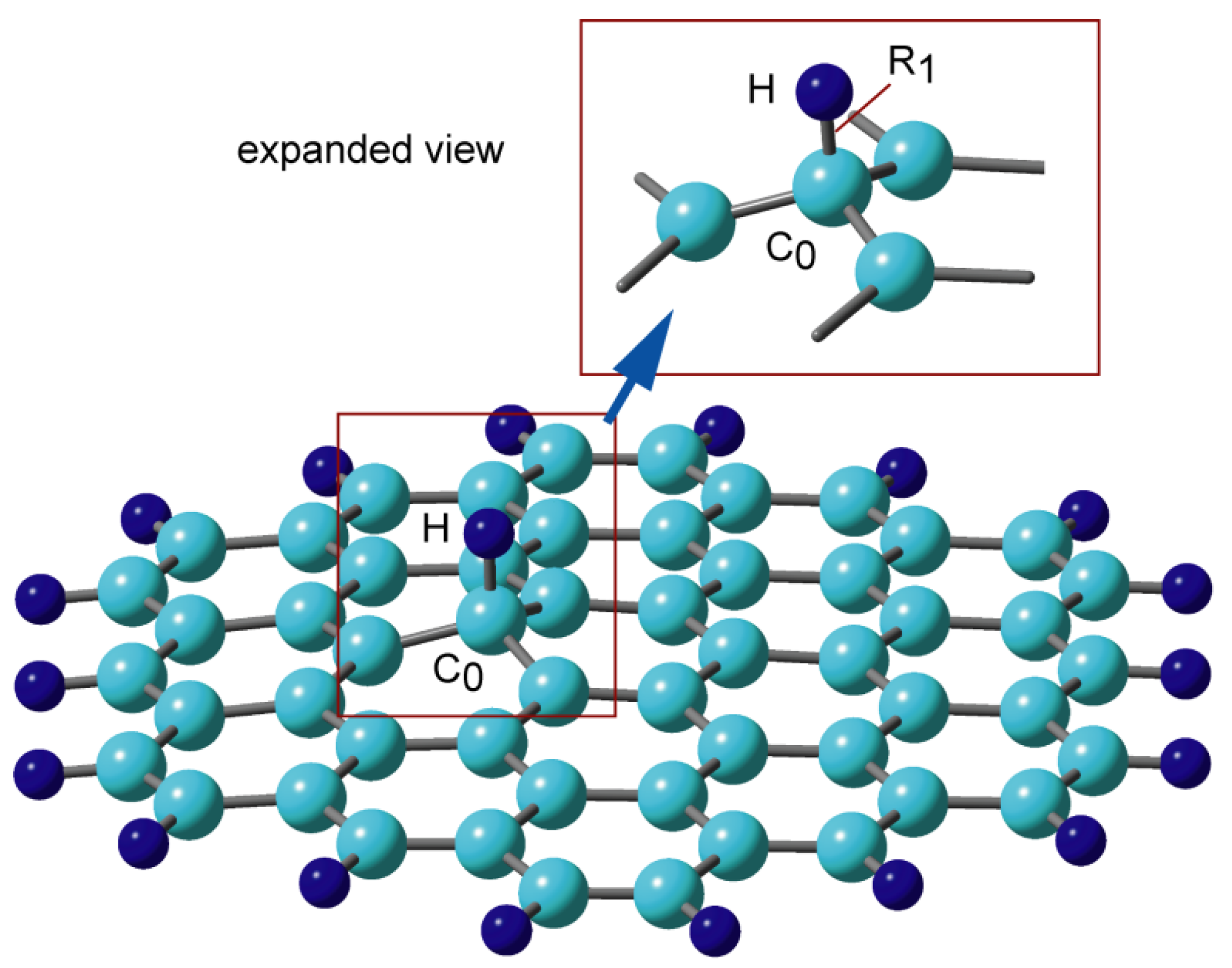
Figure 2. Binding structure of hydrogen atom to graphene nanoflake, H-GNF(19) calculated at the CAM-B3LYP/6-311G(d, p) level. Reprinted with permission from [20] (Tachikawa, Appl. Surf. Sci. 2017, 396, 1335–1342). Copyright 2017 Elsevier.
2.2. Potential Energy Curve
The potential energy curve (PEC) for the approach of H to the GNF surface is plotted in Figure 3A as a function of C0-H distance (R1). The calculations are carried out at the CAM-B3LYP/6-311G(d,p) level. All geometrical parameters except for the C0-H distance (R1) are optimized at each value of R1. When H approaches the GNF surface, the first energy minimum was found at R1 = 3.50 Å, corresponding to a van der Waals (vdW) complex composed of GNF and H. The binding energy of H to GNF is 0.2 kcal/mol. The H atom is bound by vdW force to the π-orbital of the GNF surface. Subsequently, the energy barrier corresponding to transition state (TS) is found at R1 = 1.71 Å, where the barrier height is 6.2 kcal/mol relative to the dissociation limit (GNF + H). The energy decreases significantly after TS and reaches the lowest energy point corresponding to the bound state of H-GNF, i.e., the product state (PD). The barrier is caused by the change in the electronic state in the carbon atom (C0) from sp2 to sp3 upon the addition of hydrogen.
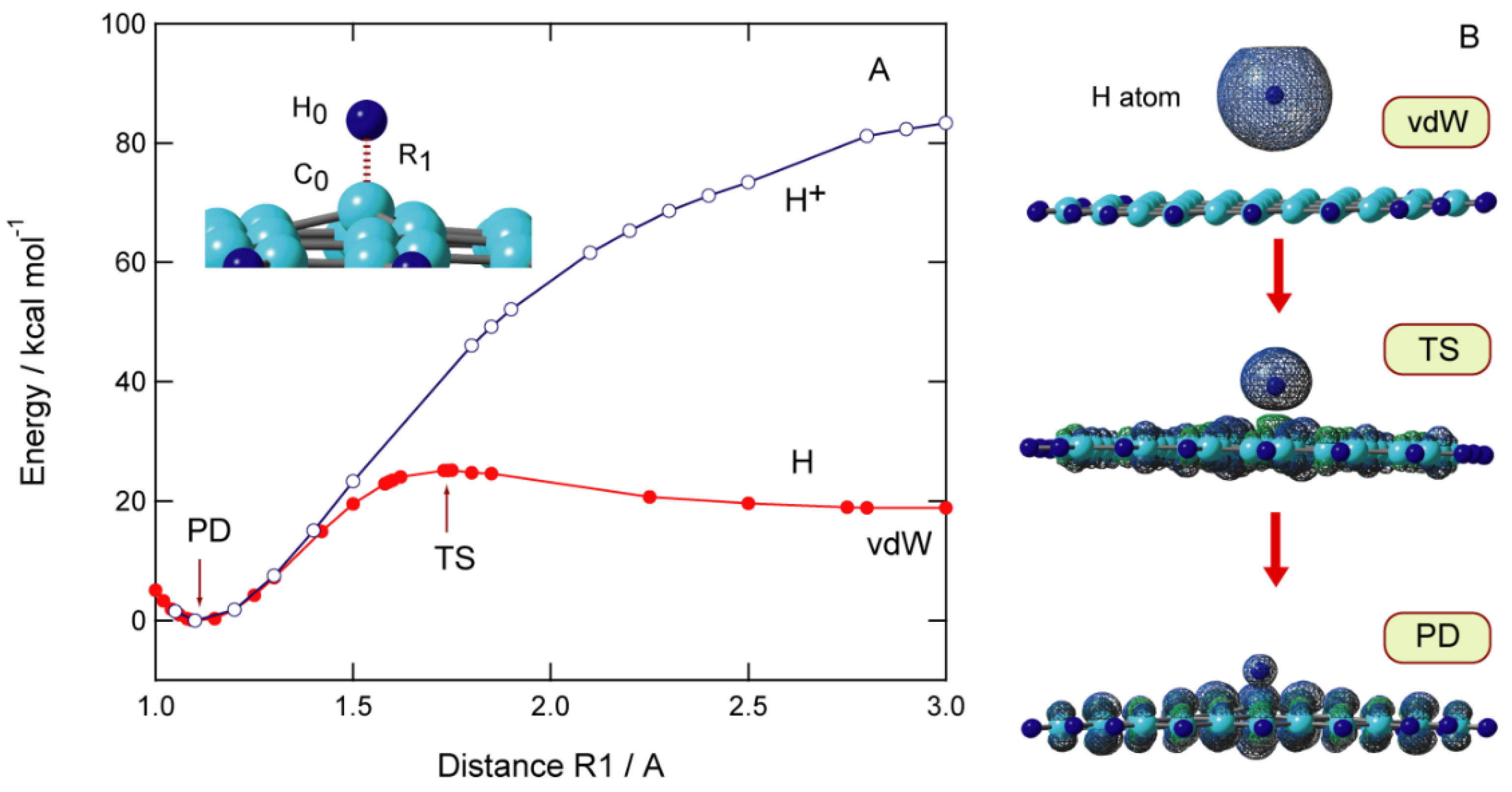
Figure 3. (A) Potential energy curves for the hydrogen atom (H) or proton (H+) addition to GNF(19), and (B) spatial distributions of spin density in H-GNF(19) along the reaction coordinate (vdW, TS, and PD states). The calculations were carried out at the CAM-B3LYP/6-311G(d,p) level. Reprinted with permission from [20] (Tachikawa, Appl. Surf. Sci. 2017, 396, 1335–1342). Copyright 2017 Elsevier.
The PEC for the addition of a proton (H+) is also given for comparison. The shape of PEC for the addition of H+ is significantly different from that of the addition of hydrogen. The H+ can bind directly to the graphene surface without an activation barrier. A large quantity of exothermic energy is generated in H+ because of the high proton affinity of GNF.
The spatial distribution of the spin density of H-GNF is shown in Figure 3B. In the vdW state, the spin density is localized to the H atom and does not flow into the PAH side. At TS, the spin density of H is 0.794, which indicates that about 20% of the unpaired electrons dissipated into the GNF side. The spin density on GNF is 0.988 in PD, indicating that the unpaired electron of the H atom is almost completely transferred to GNF.
2.3. Activation and Binding Energies
The size dependence of the activation barrier and binding energy of GNFs is shown in Figure 4. The activation energies are calculated to be 6.6 kcal/mol (n = 7), 5.6 kcal/mol (n = 14), 6.2 kcal/mol (n = 19), 5.2 kcal/mol (n = 29), and 7.0 kcal/mol (n = 37). These results indicate that the activation energy is independent of the GNF size and is nearly constant (~5–7 kcal/mol). In contrast, the binding energy was slightly dependent on the size of GNF. The binding energies for n = 14 and 29, specifically, are higher than the other binding energies.
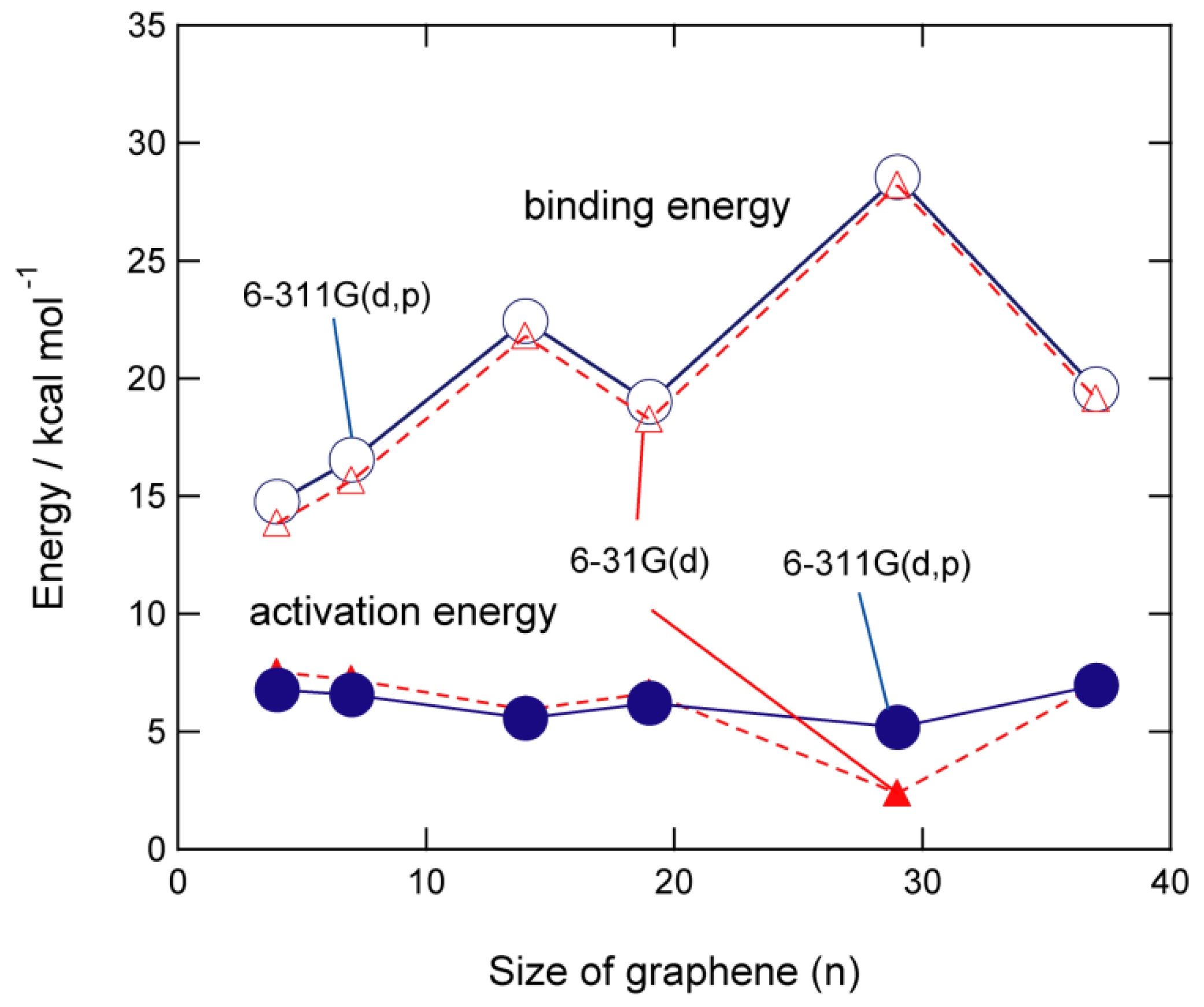
Figure 4. Binding energies (in kcal/mol) and activation energies (in kcal/mol) of hydrogen atom addition to GNF(n). The calculations were carried out at the CAM-B3LYP/6-31G(d) and 6-311G(d, p) levels of theory. Reprinted with permission from [20] (Tachikawa, Appl. Surf. Sci. 2017, 396, 1335–1342). Copyright 2017 Elsevier.
2.4. Behavior of Hydrogen Atoms on GNF (PAH) Surfaces
In this section, the interactions and reactions between H atom and GNF surface ere described, which were obtained by the DFT method. A schematic energy diagram of the interaction between the hydrogen atom and the GNF surface is shown in Figure 5. The H atom from interstellar space is first weakly bound to the GNF surface by vdW interaction. The binding energy is about 0.1–0.2 kcal/mol, and the H atom is located at 2.8–3.5 Å from the surface. This binding energy is large enough to stay on the GNF surface in interstellar space because the temperature is lower than 10 K in interstellar space. Hydrogen atoms can diffuse freely on the surface at 10 K. The diffusion barrier is about 0.2 kcal/mol. The H atom trapped on the surface in the vdW state is an active species and can readily react with other molecules. If H atom gains excess energy higher than the activation barrier, hydrogenated GNF (H-GNF) is formed. H-GNF is reactive species due to a radical with dipole moment.
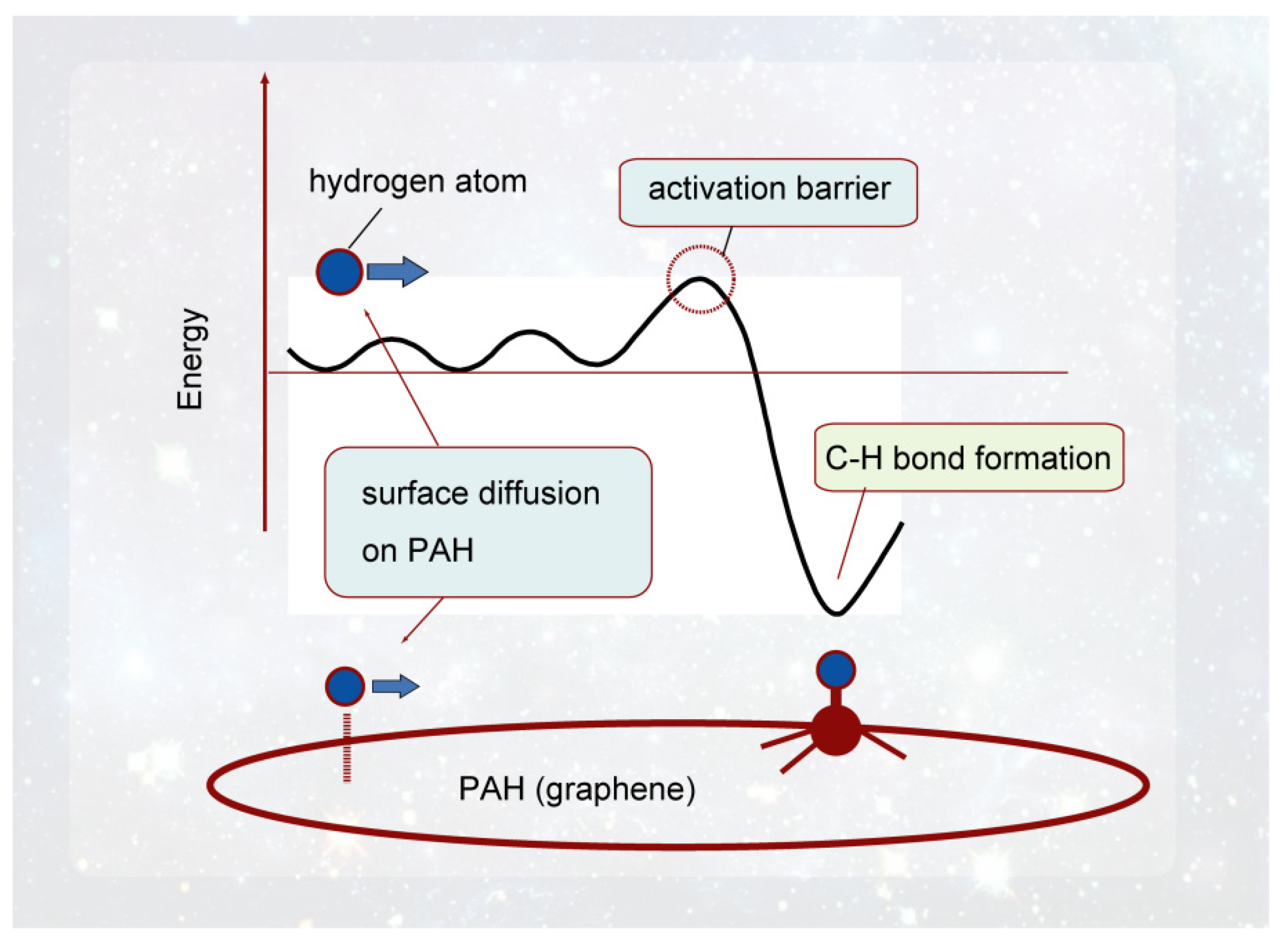
Figure 5. Schematic illustration of the interaction of hydrogen atom with PAH (graphene) surface. Reprinted with permission from [20] (Tachikawa, Appl. Surf. Sci. 2017, 396, 1335–1342). Copyright 2017 Elsevier.
3. Interaction of GNFs with Methyl Radicals
The methyl radical (CH3) is the simplest organic radical observed in interstellar space and is the basis for the formation of more complex organic molecules. It was first discovered in space by Feuchtgruber et al. [21] in Sgr A* using the infrared space telescope of the European Space Agency. It was subsequently discovered by Knez et al. in NGC7538 [22]. Methyl radicals adsorbed on GNF surfaces can evolve by reacting with other atoms and molecules[23].
In materials science, a methyl radical is an important intermediate generated from the catalytic reaction of alkane and its related compounds. The mechanism of the addition of a methyl radical to GNFs is introduced [22].
3.1. Binding Structure of Methyl Radical to GNF
The optimized binding structure of methyl radical added to GNF, CH3-GNF, is shown in Figure 6. The C-C bond distance of the binding site was calculated to be R1 = 1.574 Å. The molecular charges of CH3 and GNF parts are +0.084 and −0.084, respectively. Although CH3 shows a slight electron donor property, the magnitude of the charge transfer is very small. Therefore, CH3-GNF has no dipole moment.
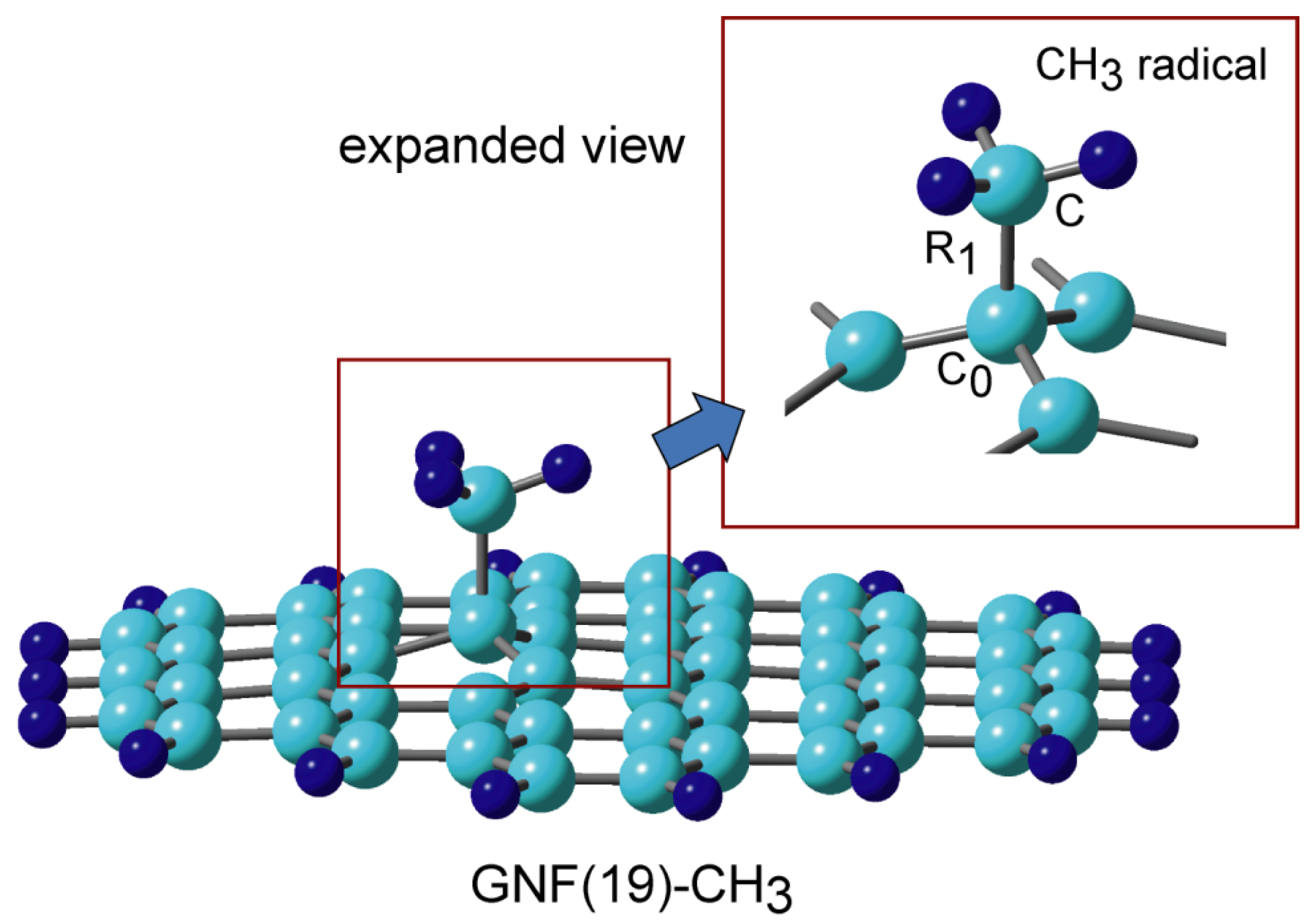
Figure 6. Binding structure of methyl radical to graphene nanoflake, CH3-GNF(19) calculated at the CAM-B3LYP/6-311G(d, p) level. Reprinted with permission from [23] (Tachikawa, Surf. Sci. 2019, 679, 196–201). Copyright 2019 Elsevier.
3.2. Potential Energy Curve
Figure 7A shows potential energy along the intrinsic reaction coordinate (IRC) for the addition reaction of CH3 to the GNF surface. The barrier height of TS is 14.0 kcal/mol higher in energy than the initial vdW complex. The distance of the CH3 from GNF in TS is R1 = 2.131 Å. After TS, the energy decreases and reaches the PD of CH3-GNF. The activation energy associated with the binding of CH3 to GNF is 14.0 kcal/mol, which is larger than that of H-GNF (6.2 kcal/mol). The addition reaction of CH3 is a 3.0 kcal/mol exothermic reaction.
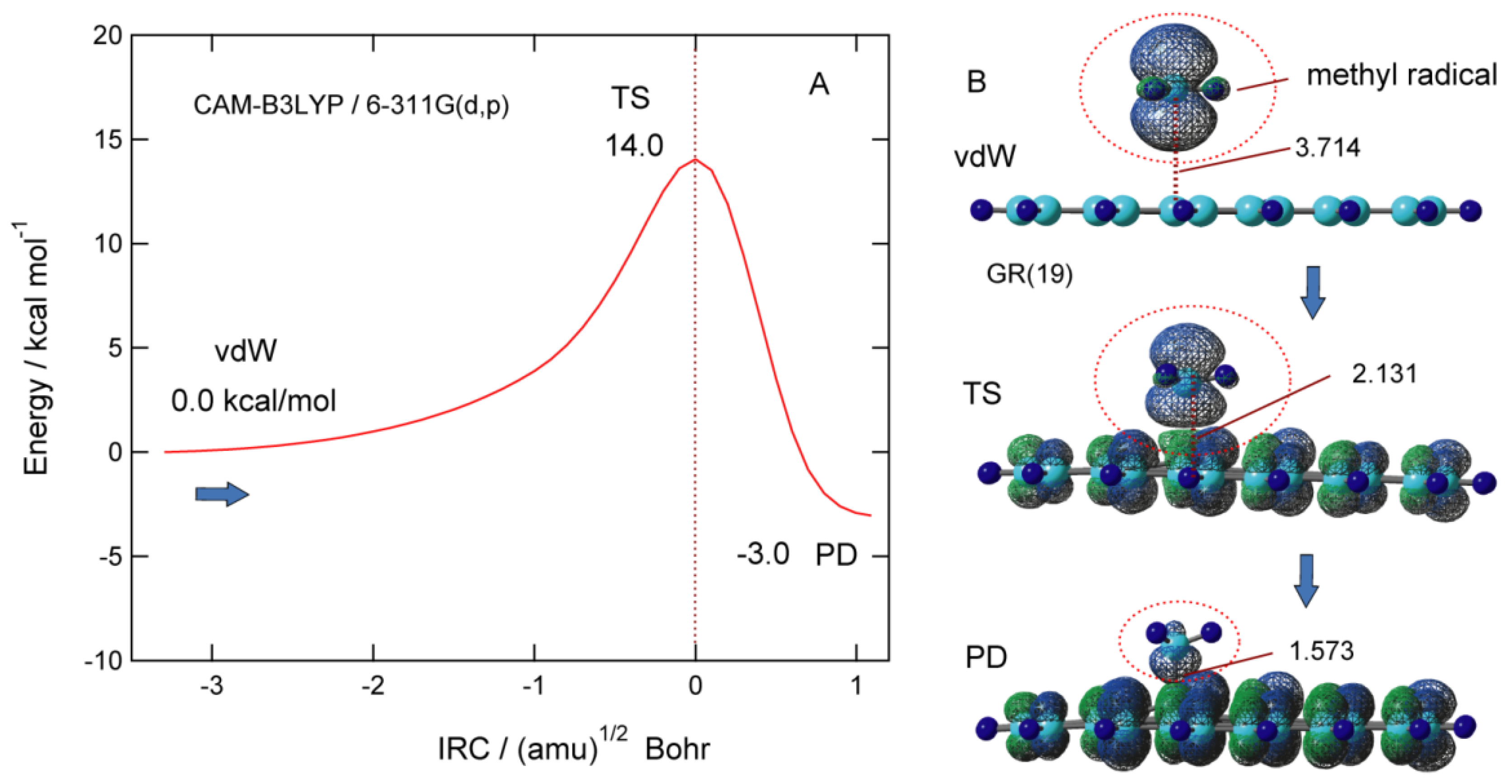
Figure 7. (A) Intrinsic reaction coordinate (IRC) for the CH3 addition reaction to GNF(19), and (B) spatial distributions of spin density in CH3-GNF(19) along the reaction coordinate (vdW, TS, and PD states). The calculations were carried out at the CAM-B3LYP/6-311G(d,p) level. The values are (A) relative energies in kcal/mol and intermolecular distance (R1) in Å. Reprinted with permission from [23] (Tachikawa, Surf. Sci. 2019, 679, 196–201). Copyright 2019 Elsevier.
The spatial distribution of the spin density of CH3-GNF is shown in Figure 7B. In the vdW state, the spin density of CH3 is 0.994, which is almost localized to the CH3 radical. In TS, the spin density of the CH3 part is 0.661 and that of GNF is 0.339, which means that almost 30% of the unpaired electrons flow from CH3 to GNF. In PD, on the contrary, the spin density of GNF is 0.931, indicating that the unpaired electron of methyl radical is almost completely transferred to GNF.
3.3. Activation and Binding Energies
The addition of CH3 to GNF needs an activation barrier. The size dependence of the activation and binding energies of GNFs. The activation energies for n = 4, 7, 19, and 37 are 15.1, 14.7, 13.8, and 13.4 kcal/mol, respectively, at the CAM-B3LYP/6-311G(d,p) level. These results indicate that there is almost no size dependence of the activation energy of GNFs. In contrast, the binding energy was slightly dependent on the size of the GNF, and the binding energy increased slightly with size.
3.4. Behavior of Methyl Radicals on GNF Surface
In this section, the interaction of CH3 with the GNF surface was described. A schematic energy diagram of the interaction between CH3 and the GNF surface is shown in Figure 8. The methyl radical from interstellar space binds weakly to the GNF surface through the vdW interaction. The binding energy is about 0.1–0.2 kcal/mol. When the methyl radical receives a quantity of kinetic energy of about 14 kcal/mol, it reacts with carbon atoms on the surface to form CH3-GNF.
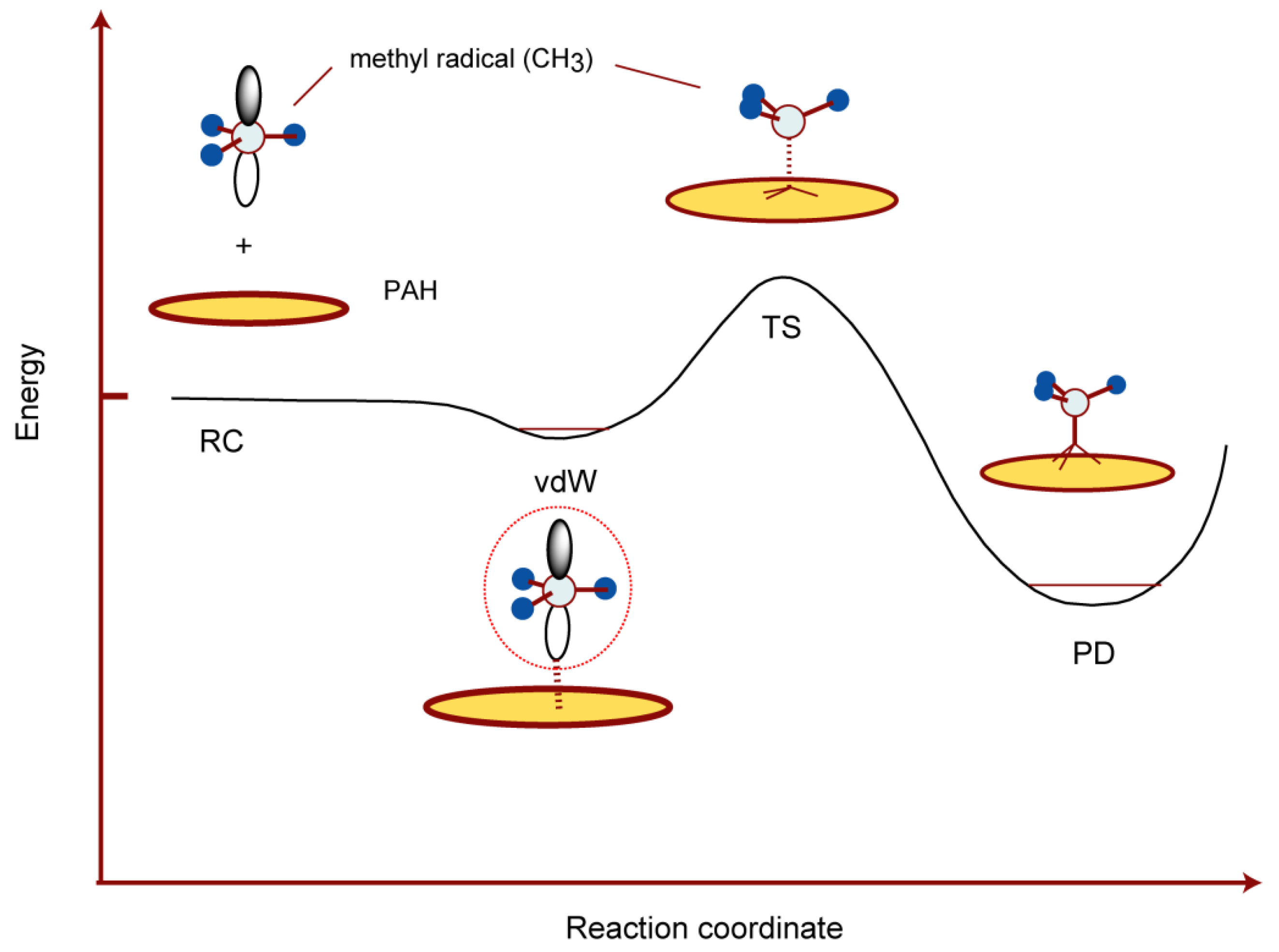
Figure 8. Schematic illustration of the interaction of CH3 with PAH (graphene) surface. Reprinted with permission from [23] (Tachikawa, Surf. Sci. 2019, 679, 196–201). Copyright 2019 Elsevier.
3.5. Activation Energies of Alkyl Radicals Addition to GNF
The activation energies of radical addition reaction, E(TS), reaction energies leading to PD, E(PD), and the binding energies of vdW complexes, E(vdW), are given in Table 1. The calculated values of methyl (CH3), ethyl (Et), n-propyl (n-Pr), iso-propyl (iso-Pr), n-butyl (n-Bu), secondary-butyl (sec-Bu), tertiary-butyl (tert-Bu), and iso-butyl (iso-Bu) radicals are given. The activation energy of CH3 is 13.8 kcal/mol, and the activation energy increases as the bulk of the molecule increases. The reaction energies are positive except for the CH3 radical, indicating that the addition of alkyl radicals is endothermic. In all radicals, vdW complexes composed of GNF and radical are exothermic formed.
Table 1. Activation energies of radical addition reaction to graphene nanoflake, E(TS), reaction energies leading to PD, E(PD), and binding energies of vdW complexes, E(vdW) (in kcal/mol). Notations are CH3, Et, n-Pr, iso-Pr, n-Bu, sec-Bu, tert-Bu, iso-Bu mean methyl, ethyl, iso-propyl, normal-butyl, secondary butyl, tertiary-butyl radicals, respectively. Zero level of relative energy corresponds to dissociation limit (radical + GNF). The calculations were carried out at the CAM-B3LYP/6-311G(d,p) level. Halogen atoms (F and Cl) can bind to GNF without activation barrier (i.e., E(TS) = 0.0 kcal/mol).
| Radical | E(TS) | E(PD) | E(vdW) |
|---|---|---|---|
| CH3 | 13.8 | −3.6 | −0.3 |
| Et | 14.7 | 1.1 | −0.6 |
| n-Pr | 15.2 | 1.3 | −0.2 |
| iso-Pr | 17.6 | 8.1 | −0.8 |
| n-Bu | 15.2 | 1.4 | −0.2 |
| sec-Bu | 18.7 | 9.7 | −0.4 |
| tert-Bu | 22.1 | 16.6 | −0.9 |
| iso-Bu | 20.1 | 9.0 | −0.7 |
| F | 0.0 | −29.4 | -- |
| Cl | 0.0 | −6.5 | -- |
References
- Pandey, G. Chemical elements in the Universe: Origin and evolution. J. Astrophys. Astr. 2020, 41, 31.
- Phua, Y.Y.; Sakakibara, N.; Ito, T.; Terashima, K. Low Temperature Plasma for Astrochemistry: Toward a Future Understanding with Continuous and Precise Temperature Control. Plasma Fusion Res. 2020, 15, 1506041.
- Kauffman, S.; Jelenfi, D.P.; Vattay, G. Theory of chemical evolution of molecule compositions in the universe, in the Miller-Urey experiment and the mass distribution of interstellar and intergalactic molecules. J. Theor. Biol. 2020, 486, 110097.
- Dwek, E.; Arendt, R.G.; Fixsen, D.J.; Sodroski, T.J.; Odegard, N.; Weiland, J.L.; Reach, W.T.; Hauser, M.G.; Kelsall, T.; Moseley, S.H.; et al. Detection and Characterization of Cold Interstellar Dust and Polycyclic Aromatic hydrocarbon Emission, from COBE Observations. Astrophys. J. 1997, 475, 565–579.
- Mori, T.I.; Onaka, K.; Sakon, I.; Ishihara, D.; Shimonishi, T.; Ohsawa, R.; Bell, A.C. Observational studies on the Near-infrared Unidentified Emission Bands in Galactic H II regions. Astrophys. J. 2014, 784, 53.
- Vats, A.; Pathak, A.; Onaka, T.; Buragohain, M.; Sakon, I.; Endo, I. Theoretical study of infrared spectra of interstellar PAH molecules with N, NH, and NH2 incorporation. Publ. Astron. Soc. Jpn. 2022, 74, 161–174.
- Hu, X.; Yang, Y.; Zhang, C.; Chen, Y.; Zhen, J.; Qin, L. Gas-phase laboratory formation of large, astronomically relevant PAH-organic molecule clusters. Astron. Astrophys. 2021, 656, A80.
- Yang, Y.; Zhang, C.; Hu, X.; Zhang, D.; Chen, Y.; Zhen, J.; Qin, L. Gas-phase laboratory study on PAH/amino-acid cluster cations. MNRAS 2021, 508, 3009–3022.
- Qu, J.; Dai, X.-X.; Cui, J.-S.; Chen, R.-X.; Wang, X.; Lin, Y.-H.; Verduzco, R.; Wang, H.-L. Hierarchical polyaromatic hydrocarbons (PAH) with superior sodium storage properties. J. Mater. Chem. A 2021, 9, 16554–16564.
- Hjertenaes, E.; Andersson, S.; Koch, H. Potential Energy Surfaces and Charge Transfer of PAH-Sodium-PAH Complexes. Chemphyschem 2016, 17, 2908–2915.
- Munoz-Castro, A.; Gomez, T.; MacLeod Carey, D.; Miranda-Rojas, S.; Mendizabal, F.; Zagal, J.H.; Arratia-Perez, R. Surface on Surface. Survey of the Monolayer Gold-Graphene Interaction from Au12 and PAH via Relativistic DFT Calculations. J. Phys. Chem. C 2016, 120, 7358–7364.
- Gloriozov, I.P.; Demyanov, P.I.; Zhulyaev, N.S.; Nechaev, M.S.; Oprunenko, Y.F.; Gam, F.; Saillard, J.-Y.; Kuznetsov, A.E. DFT Investigation of the eta(6) reversible arrow eta(6)-Inter-ring Haptotropic Rearrangement of the Group 8 Metals Complexes (+) (M = Fe, Ru, Os). J. Phys. Chem. A 2021, 125, 366–375.
- Carruthers, G.R. Atomic and Molecular Hydrogen in Interstellar Space. Space Sci. Rev. 1970, 10, 459–482.
- Sancheza, M.; Ruette, F. Hydrogen atom chemisorption and diffusion on neutral and charged polycyclic aromatic hydrocarbon (PAH) flakes in the interstellar media. Chem. Phys. Lett. 2015, 640, 11–15.
- Wang, Y.; Qian, H.-J.; Morokuma, K.; Irle, S. Coupled Cluster and Density Functional Theory Calculations of Atomic Hydrogen Chemisorption on Pyrene and Coronene as Model Systems for Graphene Hydrogenation. J. Phys. Chem. A 2012, 116, 7154–7160.
- Beitollahi, A.; Sheikhaleslami, M.A.S. A novel approach for development of graphene structure in mesoporous carbon of high specific surface area. Carbon 2016, 107, 440–447.
- Mutoh, M.; Abe, S.; Kusaka, T.; Nakamura, M.; Yoshida, Y.; Iida, J.; Hiroto Tachikawa, H. Density Functional Theory (DFT) Study on the Ternary Interaction System of the Fluorinated Ethylene Carbonate, Li+ and Graphene Model. Atoms 2016, 4, 4.
- McLean, A.D.; Chandler, G.S. Contracted Gaussian-basis sets for molecular calculations. 1. Second row atoms, Z = 11–18. J. Chem. Phys. 1980, 72, 5639–5648.
- Yanai, T.; Tew, D.; Handy, N. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57.
- Tachikawa, H. Hydrogen atom addition to the surface of graphene nanoflakes: A density functional theory study. Appl. Surf. Sci. 2017, 396, 1335–1342.
- Feuchtgruber, H.; Helmich, F.P.; van Dishoeck, E.F.; Wright, C.M. Detection of Interstellar CH3. Astrophys. J. 2000, 535, L111–L114.
- Knez, C.; Lacy, J.H.; Evans, N.J., II; van Dishoeck, E.F.; Richter, M.J. High-Resolution Mid-Infrared Spectroscopy of NGC 7538 IRS 1: Probing Chemistry in a Massive Young Stellar Object. Astrophys. J. 2009, 696, 471–483.
- Tachikawa, H. Methyl radical addition to the surface of graphene nanoflakes: A density functional theory study. Surf. Sci. 2019, 679, 196–201.
More
Information
Subjects:
Chemistry, Physical
Contributors
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
1.1K
Entry Collection:
Chemical Bond
Revisions:
2 times
(View History)
Update Date:
27 May 2022
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




