Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Demeter Tzeli
 -- 6090 2022-04-29 17:32:02 |
2 format corrected.
Beatrix Zheng
 + 1 word(s) 6091 2022-05-05 04:41:18 | |
3 references added.
Beatrix Zheng
 Meta information modification 6091 2022-05-05 07:57:28 | |
4 format corrected.
Beatrix Zheng
 Meta information modification 6091 2022-05-05 08:05:56 | |
5 format corrected.
Beatrix Zheng
 Meta information modification 6091 2022-05-05 08:07:55 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Tzeliou, C.; Mermigki, M.; Tzeli, D. Application of Quantum Mechanics/Molecular Mechanics Methodologies to Metalloproteins. Encyclopedia. Available online: https://encyclopedia.pub/entry/22516 (accessed on 25 December 2024).
Tzeliou C, Mermigki M, Tzeli D. Application of Quantum Mechanics/Molecular Mechanics Methodologies to Metalloproteins. Encyclopedia. Available at: https://encyclopedia.pub/entry/22516. Accessed December 25, 2024.
Tzeliou, Christina, Markella Mermigki, Demeter Tzeli. "Application of Quantum Mechanics/Molecular Mechanics Methodologies to Metalloproteins" Encyclopedia, https://encyclopedia.pub/entry/22516 (accessed December 25, 2024).
Tzeliou, C., Mermigki, M., & Tzeli, D. (2022, April 29). Application of Quantum Mechanics/Molecular Mechanics Methodologies to Metalloproteins. In Encyclopedia. https://encyclopedia.pub/entry/22516
Tzeliou, Christina, et al. "Application of Quantum Mechanics/Molecular Mechanics Methodologies to Metalloproteins." Encyclopedia. Web. 29 April, 2022.
Application of Quantum Mechanics/Molecular Mechanics Methodologies to Metalloproteins
Edit
This entry is adapted from the peer-reviewed paper 10.3390/molecules27092660

The multiscaling quantum mechanics/molecular mechanics (QM/MM) approach was introduced in 1976, while the extensive acceptance of this methodology started in the 1990s. The combination of QM/MM approach with molecular dynamics (MD) simulation, otherwise known as the QM/MM/MD approach, is a powerful and promising tool for the investigation of chemical reactions’ mechanism of complex molecular systems, drug delivery, properties of molecular devices, organic electronics, etc. Applications of the QM/MM methodologies on metalloproteins are presented.

 

multiscale calculations QM/MM DFT semi-empirical molecular dynamics molecular mechanics metalloproteins chemical reactions nitrogenase FeMoco

1. Introduction

Warshel and Levitt introduced the multiscaling Quantum Mechanics/Molecular mechanics approach, i.e., QM/MM, for the investigation of complex molecular systems in 1976 [1]. This methodology was first applied to an enzymatic reaction. The extensive acceptance of this method started in the 1990s [2]. In this research, the conjunction of SE methods with molecular force field was completely illustrated, while the precision, and efficacy of the QM/MM treatment in opposition to ab initio and experimental data were estimated [2]. In the last few decades, a lot of simulations for biomolecular systems have been carried out using QM/MM approaches. Moreover, a lot of reviews evaluate these methods themselves and the updates that are established throughout the years. Additionally, this method is combined with others, such as methods that consider the quantum nature of atomic motion, including free-energy and reaction path methods for more accurate answers in studies of complex systems and especially in enzymatic reactions [3]. Generally, the QM/MM approach is established for modeling complex biomolecular systems, inorganic, organometallic, and solid-state systems, as well as for the study of processes that take place in explicit solvent [3].
In 2013, the Nobel Prize in Chemistry was awarded to Martin Karplus, Michael Levitt and Arieh Warshel equally, “for the development of multiscale models for complex chemical systems” as a reward for their significant contribution in computational chemistry. The theoretical calculations based on this theory can predict chemical processes, explain, and interpret experimental data [4]. Additionally, they are supplemental to the experimental information adding details. Karplus, Levitt and Warshel’s work is revolutionary because they combined the classical consideration of matter with quantum physics and chemistry. Until then, only one type of methodology had to be chosen, i.e., classical or quantum. Classical physics approached large molecules in a simpler way which was an advantage when calculating, counter to its weakness that is the incapacity of simulation of chemical reactions. On the contrary, the quantum consideration of systems can be applied only in small systems, since it demands enormous computing power. As a result, they could be applied for small molecules only. The QM/MM theory solves this impasse of choice, and it combines both theories for a more accurate simulation [4].
Multiscaling methodologies QM/MM and QM/MM/MD [5][6][7][8][9] that combine the quantum mechanical description of specific interactions, for instance metal-ligand ones, with classical sampling of the entire system, for instance protein structure, are promising and powerful tools for computational chemistry. The studied system is split to regions. The most important area, i.e., the area where the chemical process is occurred, is calculated via a QM methodology, i.e., DFT [10] [11] [12]or SE [13][14][15]; the surrounding is studied with a less accurate method, i.e., SE or MM [16][17]; while the environment with an MM approach, or via the use of a dielectric constant for the solvent, or via MD simulations [18][19]. In the last case, the trajectories of the particles of the studied system are predicted.

2. Metalloproteins

Μetalloproteins are proteins having a metal ion cofactor [20]. Metalloproteins can be found in many living species. It is regarded that half of all recorded proteins consist of a metal compound, while the metal compounds play a determinative role in their function in some of these cases [21][22]. Metalloproteins have a variety of functions, i.e., they storage and transport elements that are significant in a cell’s living or they transport even larger molecules. One of the most important functions is the catalysis of various chemical reactions that occur in a cell’s environment [20][23]. The most common metal elements found in the metalloproteins of a human body are Fe, Mn, Zn, Co, Ni and Cu, and they are considered to be of vital importance. However, the metals are not always a part of the active center of the protein or assist the protein’s involved processes. Thus, they can just be carried and transported by the protein [24].
There are two major groups of reactions related to metalloproteins. First, there are reactions which lead to the formation of metalloproteins. This group seems almost too complicated to be studied by a MM/MD simulation and there is limited literature on this topic. The second group of reactions, which is more often studied via MM/MD simulations, includes reactions that occur when the metalloprotein acts as a reactant or a catalyst. The increase in computational capacity and the theoretically development of simulation approaches in conjunction with the experimental data (crystallography) have resulted in further clarification of the way that metal clusters are assembled or inserted into target proteins. Additionally, the catalytic pathways of such a range of complex chemical reactions by metalloproteins is clarified and explained [11].
The computational characterization of metalloproteins can be an exceptionally difficult task. The presence of a metal cations is responsible for strong Coulomb forces that act on charged amino acids and the rest of the molecule. Proteins respond dramatically to the insertion or extraction of metal cations. Significant conformational modifications are observed and even aggregations occur. Metals having partially occupied d atomic orbitals favor specific coordination geometries. Regarding the metal, the geometry of the whole molecule and the dynamics of the surroundings and of the environment may or may not favor these coordination modes. Variations from the desired geometry decrease the protein-metal binding affinity. Note that, the electronic structure of a metal is directly affected from its surroundings. The electronic configurations of the metal depend on its ligands. Thus, the metal’s electronic structure and geometry of the molecule are strongly related with each other. Any modification of each one causes changes to the other one [25][26][27][28][29][30][31][32][33][34].
In this entry, the researchers are going to focus on important computational studies using different approaches which have been conducted for some vital metalloproteins, while attention is given to nitrogenase and its FeMo cofactor.

2.1. Reactions of Metalloproteins

DFT approach usually is employed for a quantitative estimation of the complexation energies of several transition metal cations. The selectivity of metal-binding sites is investigated calculating the interaction energies between cations and its environment. Simple molecules with a general formula [MXn]a+ (where Xi’s are simplified ligands representing the protein environment) are studied and the energies of the transition metal ion complexation are evaluated. When small and large representations of metal-binding sites, i.e., small and large L ligands, are compatible with each other, useful information for reaction in even bigger systems are provided, see for instance [26][27].
The effect of specific groups or bonds on the properties and functions of proteins are studied also by using simplified ligands. For example, in the case of oxymyoglobin, which is a single chain globular protein, the hydrogen-bonding effect on Mössbauer spectroscopic properties is studied, for various active site models [27]. A porphyrin is used for representation of the heme group, and it is found that the H-bond between an His residue and the diatomic O2 enhances the binding of oxygen in the active center of protein [27].
It should be noted that metalloproteins’ metal centers present versatile chemical reactivity. The use of single-molecule atomic force microscopy (AFM) induces partial unfolding and exposes the metal centers. The rubredoxin is the first metalloprotein that has been studied via single molecule AFM in detail. QM/MD calculations on rubredoxin descripted in detail its unfolding and the breaking mechanism of ferric–thiolate bonds in different solvent conditions [34].
QM/DMD (discrete MD) approach works through a repetitious approach between QM and DMD [28][29]. DMD is a simplified MD, where discrete step function potentials are employed in the place of the continuous potential which are employed in common MD. Thus, the ballistic equations of motion are solved only for the species participating in a collision. In all, the QM/DMD predicts the structures of the metalloproteins, in agreement with X-ray experiment, as well as specific structural details, such as bond lengths of weak hydrogen bonds and their variations upon mutations in the protein. The method also can reintroduce the protein’ structure to equilibrium after a mild distortion due to the property of the combined potential energy function reaching its minimum at the intrinsic structure [25]. Up to now, it has been successfully used for the study of the function of ARD (acireductone dioxygenase) enzyme, which catalyzes two different oxidation reactions, depending only on which ion is bound to the protein, Fe2+ or Ni2+. The interconversion between the Fe2+-ARD and Ni2+-ARD is simple. Both forms of ARD were found that have different functions and the QM/DMD approach was an ideal methodology for the research of this interconversion [29]. Additionally, it has also successfully used in the modeling of the ion exchange, Ca2+ versus Mg2+, in the catechol-O-methyl transferase (COMT) enzyme, in the Fe-S electron-transporting protein rubredoxin and in several of its mutants [25].
Furthermore, in some proteins, the metal replacement can result in large-scale changes in geometry, protein motions and repacking, as is the case of COMT enzyme. COMT is enzyme involved in the physiology of pain. COMT has a Mg2+ cation, which can be interchanged with a variety of cations. This replacement results to significant alters in the structure and the activity of the enzyme. It influences the catalytic function, suppress it or it turns the enzyme to be an inhibitor. The inhibition is found that it is a simple geometric result. Multi-scaling calculations explains all mechanistic paths [29].
The metal-MFCC approach, namely metal molecular fractionation with conjugate caps, has been developed for efficient linear-scaling QM calculation of the potential energy and for atomic forces of metalloproteins. The protein’s potential energy is computed as a linear combination of (i) the potential energies of the neighboring residues, (ii) the 2-body interaction energy between non-adjacent residues, which are closely located, and (iii) the potential energy of the metal binding group. Each individual fragments in metal-MFCC can be calculated independently, so as the approach to be suitable for massively parallel computations. Thus, as the size of the studied system is increased, the computational cost of the QM calculation for the whole system increases rapidly. On the contrary, the computational cost of the metal-MFCC method increases almost linearly. It has been found that the metal-MFCC is in good agreement with full QM approach [30].
Recently in 2021, multiscale quantum refinement methods, combining several multiscale computational schemes with experimental data obtained from X-ray diffraction, were developed for metalloproteins. Different ONIOM combinations of QM, SE, and MM methodologies were used to check the performance and reliability on the refined local structure in two specific metalloproteins. It was found that ONIOM (QM/SE/MM) approach presented good results with low computational costs compared to the more expensive QM/SE approach [31]. This approach takes advantage of different flexible ONIOM schemes and experimental (XRD) information, in which the demanding transition-metal binding site is described with an efficient and accurate QM method, while the remaining system and its interactions are approximated by much faster computational low-level methods. Thus, this QM/SE/MM approach was proposed as a very good choice for computation of metal binding site(s) in metalloproteins with high efficiency.
Gallium cation, Ga3+, can mimic the ferric ion, Fe3+, and as a result it intervenes to some processes in which ferric cofactors are required. Thus, Ga3+ as a salt is used to fight various types of cancer and infectious and inflammatory diseases. However, they present some differences, for instance, Ga3+ ion cannot participate in redox reactions, or it has a different ability regarding the deprotonation of the bound water in aqua complexes. In summary Ga3+ and Fe3+ are distinguishable for some biological processes. The interactions of cations with protein ligands play a key role in their competition. These systems have been calculated via DFT, while the surroundings were represented by an effective dielectric constant. The DFT results explain and confirm the experimental findings, while they result in significant conclusions regarding the binding affinity of cations with respect to the change of the pH and of the environment [32].
The electron-transfer rates and the electronic-coupling interactions in proteins have been calculated and compared with available experimental data for a series of ruthenated azurins [33]. The DFT data are in good agreement with the experimental ones. The conformers with the strongest electron-coupling dominate on the electron-transfer rate, while the averaging, over all thermally accessible conformers of the protein and of the redox cofactors, is crucial. It is concluded that electronic coupling values based on calculations reproduce the coupling-limited experimental rates when the rates are averaged over ligand-field states and thermally accessible geometries [33].
Many studies regarding the use of MD and QM/MM in metalloproteins have been conducted. For instance, a combination of docking, QM/MM methods, and MD simulation has been used for binding affinity estimation of metalloprotein ligands [35]. Additionally, heme-containing proteins, due to their physiological importance, have been extensively characterized by computational methods and were the first protein class to be studied by MD simulations with Karplus’s work on myoglobin [36]. QM/MM calculations with DFT have been carried out for considering protein effects on the EPR and optical spectra of metalloproteins. Here, plastocyanin was used as a case study [37]. The QM/MM method has also been used to assess metalloproteins, human deacetylases, which are targets for a variety of medical conditions including neurodegenerative diseases and HIV infection. The method has also been proved to be capable of describing the kinetic differences associated with replacing Zn2+ with other metal co-factors [38]. In another case, the key step in the reaction mechanism of multicopper oxidases—the cleavage of the O–O bond in O2—has been investigated using QM/MM methods [39]. In general, enzymatic reactions have been the primary target of QM/MM studies. The examples of chorismate mutase and cytochrome P450 have been highlighted. Chorismate mutase catalyses the Claisen rearrangement of chorismate to prephenate, a key step of the shikimate pathway for the synthesis of aromatic amino acids in plants, fungi, and bacteria. On the other hand, cytochrome P450 enzymes are monooxygenases that perform a variety of essential functions, such as detoxification and biosynthesis, in nearly all living species. They also catalyze many types of reactions [40]. QM/MM reaction pathway analysis has provided detailed insight into the chemistry of glutathione S-transferase and can be used to obtain mechanistic insight into the effects of specific mutations on this catalytic process [41]. A developed QM/MM modification of the Linear Response method was used to distinguish ligand affinities for closely related metalloproteins. The precision level acquired makes the approach a useful tool for design of selective ligands to similar targets, as results can be extrapolated to maximize selectivity [42]. A QM/MM study of the formation of the elusive active species Compound I of nitric oxide synthase from the oxyferrous intermediate showed that two protons should be provided to produce a reaction that is reasonably exothermic and that leads to the appearance of a radical on the tetrahydrobiopterin cofactor [43]. QM/MM calculations have been employed to investigate the role of hydrogen bonding and π-stacking in single- and double-stranded DNA oligonucleotides [44]. MD simulations of metalloproteins were also carried out in a folding study of rubredoxin from Pyrococcus furiosus [45].

2.2. Nitrogenase and FeMo Cofactor

2.2.1. General about Nitrogenase—Structure

Nitrogenase is one of the most fascinating natural metalloenzymes. It is produced by certain prokaryotes, such as cyanobacteria and it is essential for all living beings. Nitrogenase catalyzes an essential step of procedures in nitrogen fixation, where the reduction in the N2 to NH3 occurs through a complex and multistage reactions [19][46][47][48][49][50][51][52][53][54][55][56][57][58][59][60][61][62][63][64][65][66][67][68][69][70][71][72][73][74][75][76][77][78][79]. Ammonia is vital for all species, because of its essential role in synthesis of biomolecules such as nucleotides and amino acids. Despite the fact that N2 is abundant in the earth’s atmosphere, it is essentially inert at room temperature without a suitable catalyst. That leads to the vital role of nitrogenase. As a result, the scientific community is highly interested to study properly this reaction both through experiments and simulations. It is known that Nif genes or homologs have the information to correct creation of nitrogenase [46][47].
Regarding the structure of this molecular system, see Figure 1, it contains two metalloproteins, the homodimeric iron (Fe-) protein, which is a great reductase and is responsible for the electrons’ supply. It is a dimer of two identical subunits. They are connected through two covalent bonds with one [Fe4S4] cluster [48]. (Fe-) protein is responsible for electron transfer from a reducing agent, such as ferredoxin or flavodoxin, to the nitrogenase protein (MoFe-) protein. This transfer demands an input of chemical energy. It can be covered by the binding and hydrolysis of ATP. A configuration change occurs because of the hydrolysis of ATP within the whole complex. Note that the two main metalloproteins are brought closer together so the electron transfer is easier to occur [49].
The second part of the nitrogenase complex is the heterotetrameric α2β2 or heterodimeric (αβ)2 molybdenum-iron (MoFe-) protein, where electrons are used for the conversion of Ν2 to ΝH3. It consists of two α and two β subunits [48]. MoFe-contains two identical iron-sulfur [8Fe-7S] clusters, namely P-clusters. They are located at the interface between the α and β subunits, counter to the other feature clusters, the two FeMo cofactors (FeMoco), which show up within the α subunits. Both subunits are of similar size and are encoded by the rifD and nifK genes [50]. The Mo cation is considered to be Mo(III), contrary to Mo(V) that prevailed earlier [51]. The [Fe8S7] core of the P-cluster consists of two cubes [Fe4S3] linked by a carbon atom. The two P-clusters are connected via covalent bonds with the rest of MoFe-through bridges that consist of six cysteine residues. Moving on to the two identical FeMo cofactors [MoFe7S9C], each contains two different clusters, i.e., [Fe4S3] and [MoFe3S3]. The last ones are linked by three sulfide ions. One cysteine and one histidine residues are used to connect each FeMo cofactor with the α submit through covalent bonds. Regarding the role of every part of the nitrogenase complex, the Fe- protein provides electrons that are entered to the P-clusters of the MoFe-protein. Then, they are transferred from the P-clusters to the FeMo cofactors, where the nitrogen fixation occurs, and the dinitrogen is connected in the central cavity of the FeMoco [46].
Some variations of this complex appear in nature. Thus, two types of such nitrogenases have been confirmed: the vanadium-iron type (VFe; Vnf) and the iron-iron type (FeFe; Anf), where the (MoFe-) protein is replaced. There are 2 α, 2 β and 2 δ or γ subunits instead of (αβ)2 of the usual complex [52][53]. Nevertheless, molybdenum nitrogenase, is the one that has been studied more extensively, because of its abundance versus the others and is thus the most well characterized [46].
/media/item_content/202205/627367bd55b17molecules-27-02660-g001.png
Figure 1. Structure of Nitrogenase complex [54].

2.2.2. General Mechanism

As mentioned before, the reduction in N2 to NH3 demands a catalytic route to occur because of inaction of N2. The required activation energy for the reduction is large (Ea = 230–420 kJ mol−1), but the enthalpy is negative (ΔH° = −45.2 kJ mol−1). This means that the whole reaction is thermodynamically favorable [55]. All these are also confirmed through the industrial fixation of N2 by the Haber-Bosch process, where this specific reduction takes place in temperatures ranging from 300 to 500 °C, while the pressures are more than 300 atm. The presence of Fe-based catalysts is necessary [47].
Continuing with the reduction in the substrate by nitrogenase, three basic steps occur where electrons are transfers. Firstly, the reduction in (Fe-) protein is occurred where electrons are transferred from electron carriers such as ferredoxinor or flavodoxin in vivo or dithionite in vitro to (Fe-) protein. The second step is described by the transfer of single electrons from (Fe-) to (MoFe-) protein in an MgATP-dependent process. A minimal stoichiometry of two MgATP are hydrolyzed per electron. The last e− transfer occurs to the substrate which is almost certainly bound to the active site of the (MoFe-) protein [46]. The overall stoichiometry of N2 reduction by nitrogenase has been established as [47]:
N2 + 8 H+ + 16 MgATP + 8 e− → 2 NH3 + H2 + 16 MgADP + 16 Pi
Studying the general equation of this reaction, nitrogenase also catalyzes the reduction in H+ to H2 (which is necessary for the formation of NH3) along with the reduction in dinitrogen to ammonia. Additionally, it catalyzes the reduction in other small unsaturated molecules such as azide, cyanide, acetylene [56].
The Lowe-Thorneley (LT) kinetic model, is the one that has been established for the whole process and was developed experimentally, see Figure 2. Eight H+ and eight e− are transferred during the reaction [47][48][57][58]. Each intermediate stage is represented as En, n = 0–8, which is proportionate to the numerous of the equivalents thar are transferred. The connection of N2 with the complex occurs at the stage E4, where four equivalents have already been transferred [48]. However, N2 sometimes binds to nitrogenase at the stage E3.
/media/item_content/202205/627367e226714molecules-27-02660-g002.png
Figure 2. Lowe-Thorneley kinetic model adapted from [58].
This model was based on spectroscopic data that were selected throughout the process. The clarification of the mechanism is still an active area of research and a debate for the scientific community. The E0 state is the initial one where the enzyme rests at equilibrium before the catalysis begins [59]. The reductions begin at the E1 state where an e− is transferred to the (Fe-) protein, with the escort of a proton (H+). The intermediate state E2 is described by the metal cluster being in its resting oxidation state, the two added e− deposited in a bridging hydride, while the additional H+ is bonded to a sulfur atom. Lastly before the dinitrogen connection to the complex, the single reduced FeMo cofactor with one bridging hydride and one H+, belong to the E3 state. Moving on, the E4 state is considered to be a critical stage and takes part in the middle of the catalytic cycle. It appears after the accumulation of 4 pairs of electrons and protons, and it is named as Janus intermediate because of its dynamic nature. The system can decay back to E0, aborting the pairs that were collected or it can proceed with nitrogen binding and complete the catalytic cycle. The FeMo cofactor appears to be in its resting oxidation state with two bridging hydrides and two sulfur bonded H+ [47].
Based on the above intermediate states, a dynamic equilibrium is proposed for the oxidation states of the metal cluster, and especially between its initial oxidation state and a singly reduced one with additional electrons which are stored in hydrides. On the other hand, it is considered that in each step, the formation of a hydride occurs and that the metal cluster exists between the initial oxidation state and the single oxidized one [47].
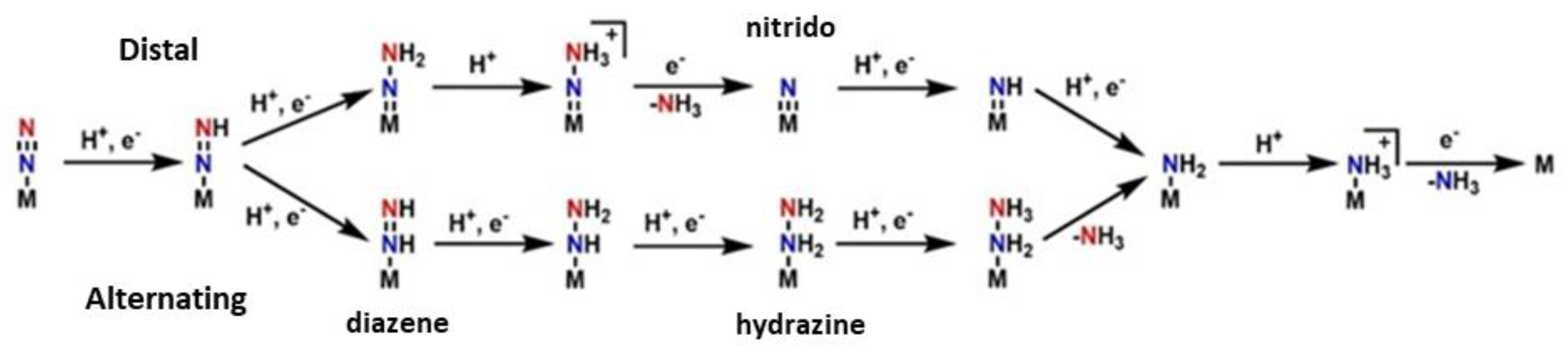
Moving on towards the production of the ammonia, two basic hypotheses exist for the pathway in the second half of the mechanism: the “distal” and the “alternating” pathway, c.f. Figure 3. In the “distal” route, the dinitrogen is firstly hydrogenated on the one atom of nitrogen, leading to the release of ammonia and then the second nitrogen, which is directly bound to the metal, is hydrogenated. In the “alternating” route, the nitrogen atoms are hydrogenated alternately. This pattern goes on until NH3 is released from both nitrogen atoms [46][60]. It has not been clarified which pathway is correct and occurs at last. The solution to this, is the isolation of forementioned intermediates, such as the nitrido in the “distal” route and the diazene and hydrazine in the “alternating” route. However, many more problems occur from this process. The use of model complexes helps the isolation of intermediates but there is a metal center dependance. When Molybdenum model complexes are studied, the distal way predominates counter to the Iron model complexes, where the alternating pathway is preferred from the system [47].
/media/item_content/202205/627367ff22cddmolecules-27-02660-g003.png
Figure 3. Nitrogen Fixation Mechanism adapted from [47] and [80].

2.2.3. Calculations

Many calculations have been performed throughout the years for this complex system and attention has been given to its catalytic role in the nitrogen fixation process. The included clusters and the cofactor have been studied and characterized independently, while there are studies of the whole complex of the metalloenzyme. Here, a research on the calculations of the states En that were involved in the proposed mechanism is presented.
DFT calculations have been carried out for the MoFe cofactor [MoFe7S9C], including the 35 possible broken-symmetry (BS) states in the resting state, a reduced state, and a protonated state of the cofactor. The results show that the relative energies of the calculated states depend on their geometry, the environment, i.e., surrounding protein, and the choice of the methodology, i.e., DFT functionals, basis sets. Specifically, the basis sets affect the energy values of the states, i.e., up to 11 kJ/mol. The effects of the structure of the surrounding protein result to energy differences up to 7 and 10 kJ/mol for the vdW and the electrostatic energy, respectively [61].
Single-point energy calculations using experimental geometries give similar values to the energies calculated after the optimization of geometry, but some BS states differ from the experimental ones up to 37 kJ/mol. Changing the functional from the pure TPSS to the hybrid B3LYP, a difference in energies up to 58 kJ/mol is noticed, while the correlation between the two results is small, (R2 = 0.57–0.72). Nevertheless, both DFT functionals are in agreement regarding the ground spin state and the reduced one. All results related to the most stable states of the structure, are useful for further calculations on the mechanism of the catalysis leading to more accurate results [61].
Furthermore, in the above research, QM/MM calculations were carried out, using the classic set Amber ff14SB force field with TIP3P for water molecules while geometry optimization was performed through TPSS-D3 method and the def2-SV(P) basis set. It was concluded that four of the Fe ions need to have the dominant α spin and three should have the opposite β spin in order to reach the experimentally observed quartet state of the cofactor, and when in asymmetric protein, there are 35 different ways that this can occur. Last but not the least, an interesting fact was concluded, namely 3 to 6 BS states of the same C3-symmetry type had close energy values leading to the fact that the protein influences a little the relative energies of the BS states that are related by the approximate three-fold symmetry of the FeMo cofactor [61].
B. Benediktsson and R. Bjornsson have carried out a series of calculations [62] where the protein environment has been taken into account. QM/MM methods are employed to study the MoFe protein and the FeMo cofactor. They concluded that only the [MoFe7S9C]1− charge is a possible resting state charge. The result of −1, as a charge of the resting state, provides data in completely agreement with recent spectroscopic [63] and other computational studies [64]. Considering different spin isomers, the one that agrees with the crystallographic Fe−Fe and Mo−Fe distances has Fe cations with spin directions which lead to a rare case of spin-coupling phenomena. According to this research, on the alkoxide group on the Mo-bound homocitrate under resting state conditions, exist a proton. This proton affects the nature of the redox states of FeMoco and additionally affects some substrate reduction mechanisms [62].
Regarding the mechanism and the reaction states, the conjunction of theoretical and experimental data leads to the fact that formation of E1 is occurred via a Fe-centered reduction in combination with the protonation of a sulfide of the cluster [65]. An interesting fact about Thorhallsson and Bjornsson works [65][66] is that the used theoretical approaches for subsequent states En (n = 1–8) are the same with the used ones for E0 state (CHARMM36 as a force-field for MM level of theory and TPSSh hybrid density functional for QM level, respectively). Moving on with the mechanism, it is possible for, only the E0 and E1 states to be selectively populated under conditions in which the rate of H2 production from the E2 state is faster than the rate of the formation of E2. Additionally, E1 models having a protonated bridging sulfide are in total agreement with the EXAFS data. All these lead to the most likely candidates to describe the E1 state. Last but not the least, minor modulation of Mo-O, Mo-Fe, and Fe-Fe distances occur throughout the process of E0 to the E1 state and the first reduction [65].
A systematic theoretical study of the relative energies of possible protonation states of the FeMo cluster in nitrogenase in the E0–E4 states has been performed via a QM/MM approach [67]. Additionally, the resting state, the states with 1–4 electrons and protons added before N2 binding were studied. In these calculations, the complete solvated heterotetrameric enzyme has been included for more accurate results. Two different B3LYP-D3 and TPSS-D3 dispersion corrected functionals with different basis sets, def2-SV(P) and def2-TZVPD, were used and they led to different results on the E2–E4 states, counter to the E0 and E1 states. Specifically, TPSS-D3 supports hydride ions binding to the Fe ions at the E2–E4 states creating a bridge between the Fe metals. Nonetheless, B3LYP-D3 predicts that one to three H+ cations are connected to the central carbide ion and that the most energetically stable structures of the E2, E3 and E4 states have the carbide ion doubly or triply protonated. Lastly, the most favorable protonation site was found to be the S2B in the E1 state [68].
The redistribution of electrons within the active site of the FeMo-co during the reductive removal of H2 to activate the N2, has also been calculated via QM/MM MD simulations. The nitrogen fixation process starts with the binding of N2 to E4 combined with the elimination of H2 [68]. This loss cannot start in absence of N2 in E4(4H) state, despite the fact that it interconverts with E4(H2,2H). This occurs because of the resulting high-energy E4(2H)* state that causes a H2 rebind [68]. Additionally, the non-participation of the Mo site in the electron redistribution was observed as the reaction with the N2 begins and it was also found that the change of Mo’s valence electrons is unlikely to occur throughout the nitrogenase cycle. Finally, it was shown that the electron redistribution upon conversion of hydride elimination and removal of H2 from E4(4H) to E4(2H)* is activating one or both Fe cations to bind N2 in the catalytically central H2 complex, E4(H2,2H). Thus, the coupled removal of H2 and the reduction in N2 is initiated [68].
Specifically, the E4 state attract the research interest. Possible models for this state of nitrogenase and how N2 can be connected to some of these models was calculated via QM/MM approaches. Some calculations using the CHARMM36 force field for the MM approach, combined with a recent ENDOR study, result to the most favored structure of FeMo cofactor at the E4 state, see Figure 4. However, further QM calculations using hybrid functionals (B3LYP, TPSSh, M06-2X and HF exchange) lead to higher energy values for this structure counter to all open-sulfide bridge models, while this model has not been found to bind N2, which remains an open question to be investigated in [66]. Thorhallsson et al. proposed a mechanism for the E4 state. Specifically, the function of various components of the cofactor of nitrogenase is introduced. The cofactor’s size and the nature of the Fe–S bonds play a primary role. Moreover, the sulfide bridge between the cubanes increases the stability of the hydride. The molybdenum ion is likely to affect the redox potential of the cofactor and it could be vital for further stabilization of the N2-bound Fe(I) ion in E4-l-N2, which is formed after the reductive step, so that the N2 ligand to find available e−, to assist its activation. Finally, it has been proposed that the H+ on the Mo-bound alcohol group of homocitrate is in the best position, so as theN2 ligand to be protonated [66].
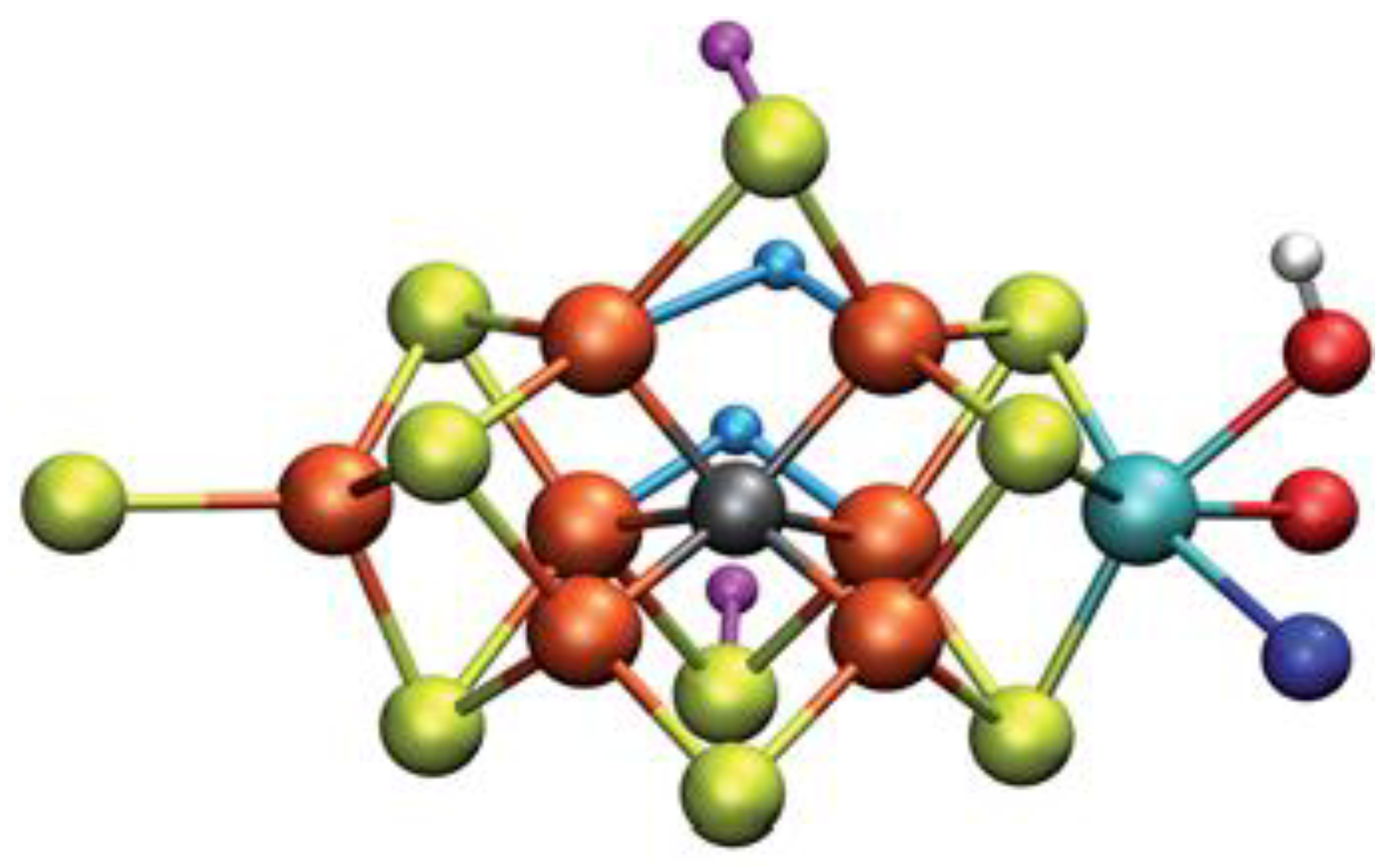
/media/item_content/202205/62736824001cbmolecules-27-02660-g004.png
Figure 4. Structure of FeMo cofactor at the E4 state [66].
In 2020, Cao and Ryde [69] carried out a QM/MM study on N2 bound state of nitrogenase assuming that N2 is instantly protonated to a N2H2 state, and thus the issue of finding the position of the H+ cations in the cluster is avoided. The Amber f14SB FF was used for the protein and the MM approach and the TIP3P model was chosen to describe water molecules in the environment. The charges were obtained at TPSS/def2-SV(P) level of theory and the non-bonded model approached the metal sites. Studying both pathways, the distal and the alternating one (HNNH and NNH2 respectively), it was found that the binding of N2H2 is mainly occurs due to the interactions and steric clashes with the protein and not due to the intrinsic preferences of the ligand and of the cluster. Regarding the energies of the calculated states, noticeable differences are observed regarding the relative energy difference of the low-lying structures, when different functionals are used [69].
To conclude, a lot of questions are still open, like the exact way in which ligands are activated for protonation. Note that it could be very useful any additional experimental data on the En states to further restrict the mechanistic possibilities of FeMo cofactor for comparison with the calculated data. Nonetheless, the published studies propose a pathway to clarify the mechanism of nitrogenase catalytic role [19][69][70][71][72][73][74][75][76][77][78][79].

3. Current Insights

The commonly used QM methodology in the QM/MM and QM/MM/MD approaches is DFT which can be used in systems up to a few hundred atoms. DFT is a computational cheap methodology comparing to ab initio methods, such as multi-reference and coupled-cluster approaches, while its accuracy is comparable to them especially when the optimal functional has be used for a particular application [9][79][81][82][83][84][85][86][87][88][89][90][91][92][93][94][95][96][97][98]. B3LYP is a commonly used functional that generally works well in many applications. For more demanding applications, there is a plethora of functionals as well as many published studies that can assist for the choice of the appropriate functional. Finally, efforts are being made for the development of functionals that will be suitable for a wide range of applications [70][94]. When DFT methodology is difficult to be applied, SE methods are used. They are built on the HF formalism, but various approximations have been considered and empirical data are used. They are valuable methodologies for studying electronic effects in large molecules of biological systems and they can be applied successfully in complex systems [15][99][100][101][102][103][104][105]. When the surrounding consists of hundreds to thousands of atoms, QM (DFT or SE) calculations are not feasible, thus the potential energy of the system is defined using a force field method, where the electronic motions are ignored, and the energy of the system is calculated as a function only of the nuclear positions. Finally, MD simulations are employed to simulate system of hundreds of atoms to macromolecules of biological interest such as ribosomes, nucleosomes, metalloproteins, etc. The range of the population of atoms of the calculated systems is up to 500,000. A dynamic model is built, for instance for proteins, where the internal motions and the subsequent conformational changes significantly affect their function [106]. Algorithms are developed to calculate the trajectories through a force field approach. There are two main approaches for MD simulations: (i) the atomistic representation used for small systems and (ii) the coarse-grained method, where molecules are represented by “pseudo-atoms” approximating groups of atoms. While the first approach is more accurate, the second one is used for metalloproteins due to the size of the studied system. However, when the system is too large, i.e., liposomes with infinite radius in terms of Å, planar bilayers can be used, and thus the system can be studied via atomistic MD simulations. On the contrary, small liposomes can be fully considered using atomic level MD. Nevertheless, liposomes are generally studied better using CG models [107].
The computational research of metalloproteins and reactions involved can be a very difficult and demanding task. The presence of the metal cations that have different coordination numbers, empty or half occupied d orbitals and low lying atomic excited states further complicate the calculations. As a result, the insertion or removal of metal cations affects proteins, large conformational changes are caused, and even aggregations are formed. Thus, the research of chemical reactions of proteins and specifically: (i) the exact reaction mechanism/pathway, and (ii) the evaluation of the properties of catalytic intermediates are very hot topics.

References

  1. Koch, W.; Holthausen, M. C. . A Chemist’s Guide to Density Functional Theory; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2001; pp. 1-293.
  2. Nitrogenase . wikipedia. Retrieved 2022-4-29
  3. Senn, H.M.; Thiel, W. QM/MM methods for biomolecular systems. Angew. Chem. Int. Ed. Engl. 2009, 48, 1198–1229.
  4. Noorden, R.V. Modellers react to chemistry award. Nature. 2013, 502, 280.
  5. Siegbahn, P.E.M.; Himo, F. The quantum chemical cluster approach for modeling enzyme reactions. WIREs Comput. Mol. Sci. 2011, 1, 323–336.
  6. Ahmadi, S.; Barrios Herrera, L.; Chehelamirani, M.; Hostaš, J.; Jalife, S.; Salahub, D.R. Multiscale modeling of enzymes: QM-cluster, QM/MM, and QM/MM/MD: A tutorial review. Int. J. Quantum Chem. 2018, 118, e25558.
  7. Vreven, T.; Morokuma, K. Chapter 3: Hybrid methods: ONIOM(QM:MM) and QM/MM. Annu. Rep. Comput. Chem. 2006, 2, 35–51.
  8. Zhou, Y.; Wang, S.; Li, Y.; Zhang, Y. Born–Oppenheimer Ab Initio QM/MM Molecular Dynamics Simulations of Enzyme Reactions. Methods Enzymol. 2016, 577, 105–118.
  9. Watanabe, H.C.; Cui, Q. Quantitative Analysis of QM/MM Boundary Artifacts and Correction in Adaptive QM/MM Simulations. J. Chem. Theory Comput. 2019, 15, 3917–3928.
  10. Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871.
  11. Te Vrugt, M.; Löwen, H.; Wittkowski, R. Classical dynamical density functional theory: From fundamentals to applications. Adv. Phys. 2020, 69, 121–247.
  12. Koch, W.; Holthausen, M. C. . A Chemist’s Guide to Density Functional Theory; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2001; pp. 1-293.
  13. Stewart, J.J.P. Optimization of parameters for semiempirical methods I. Method. J. Comput. Chem. 1989, 10, 209–220.
  14. Stewart, J.J.P. Optimization of parameters for semiempirical methods II. Applications. J. Comput. Chem. 1989, 10, 221–264.
  15. Thiel, W. Semiempirical quantum-chemical methods in computational chemistry. In Theory and Applications of Computational Chemistry: The First 40 Years; Dykstra, C.E., Kim, K.S., Frenking, G., Scuseria, G.E., Eds.; Elsevier B.V.: Amsterdam, The Netherlands, 2005; pp. 559–580. ISBN 9780080456249.
  16. Leach, A.R. Molecular Modelling: Principles and Applications; Pearson Education: London, UK, 2001; ISBN 0-582-38210-6.
  17. Cramer, C.J. Essentials of Computational Chemistry: Theories and Models; Wiley: Louisville, KY, USA, 2013; ISBN 978-0-470-09182-1.
  18. Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936.
  19. Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447.
  20. Banci, L.; Sigel, A.; Sigel, H.; Sigel, R.K. (Eds.) Metallomics and the Cell; Metal Ions in Life Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Volume 12, pp. 1–13. ISBN 978-94-007-5561-1.
  21. Thomson, A.J.; Gray, H.B. Bioinorganic chemistry. Curr. Opin. Chem. Biol. 1998, 2, 155–158.
  22. Waldron, K.J.; Robinson, N.J. How do bacterial cells ensure that metalloproteins get the correct metal? Nat. Rev. Microbiol. 2009, 7, 25–35.
  23. Carver, P.L. Metal Ions and Infectious Diseases. An Overview from the Clinic. In Interrelations between Essential Metal Ions and Human Diseases; Sigel, A., Sigel, H., Sigel, R.K., Eds.; Metal Ions in Life Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Volume 13, pp. 1–28. ISBN 978-94-007-7499-5.
  24. Maret, W. Metalloproteomics, metalloproteomes, and the annotation of metalloproteins. Metallomics. 2010, 2, 117–125.
  25. Finkelstein, J. Metalloproteins. Nature 2009, 460, 813.
  26. Sparta, M.; Shirvanyants, D.; Ding, F.; Dokholyan, N.V.; Alexandrova, A.N. Hybrid Dynamics Simulation Engine for Metalloproteins. Biophys. J. 2012, 103, 767–776.
  27. Rulíšek, L.; Havlas, Z. Using DFT Methods for the Prediction of the Structure and Energetics of Metal-Binding Sites in Metalloproteins. Int. J. Quantum Chem. 2003, 91, 504–510.
  28. Ling, Y.; Zhang, Y. Deciphering Structural Fingerprints for Metalloproteins with Quantum Chemical Calculations. Annu. Rep. Comput. Chem. 2010, 6, 65–77.
  29. Shirvanyants, D.; Ding, F.; Tsao, D.; Ramachandran, S.; Dokholyan, N.V. Discrete molecular dynamics: An efficient and versatile simulation method for fine protein characterization. J. Phys. Chem. B 2012, 116, 8375–8382.
  30. Nechay, M.R.; Valdez, C.E.; Alexandrova, A.N. Computational Treatment of Metalloproteins. J. Phys. Chem. B 2015, 119, 5945–5956.
  31. Xu, M.; He, X.; Zhu, T.; Zhang, J.Z.H. A Fragment Quantum Mechanical Method for Metalloproteins. J. Chem. Theory Comput. 2019, 15, 1430–1439.
  32. Yan, Z.; Li, X.; Chung, L.W. Multiscale Quantum Refinement Approaches for Metalloproteins. J. Chem. Theory Comput. 2021, 17, 3783–3796.
  33. Nikolova, V.; Angelova, S.E.; Markova, N.; Dudev, T. Gallium as a Therapeutic Agent: A Thermodynamic Evaluation of the Competition between Ga3+ and Fe3+ Ions in Metalloproteins. J. Phys. Chem. B 2016, 120, 2241–2248.
  34. Prytkova, T.R.; Kurnikov, I.V.; Beratan, D.N. Ab Initio Based Calculations of Electron-Transfer Rates in Metalloproteins. J. Phys. Chem. B 2005, 109, 1618–1625.
  35. Zheng, P.; Arantes, G.M.; Field, M.J.; Li, H. Force-induced chemical reactions on the metal centre in a single metalloprotein molecule. Nat. Commun. 2015, 6, 7569.
  36. Khandelwal, A.; Lukacova, V.; Comez, D.; Kroll, D.M.; Raha, S.; Balaz, S. A Combination of Docking, QM/MM Methods, and MD Simulation for Binding Affinity Estimation of Metalloprotein Ligands. J. Med. Chem. 2005, 48, 5437–5447.
  37. Banci, L. Molecular dynamics simulations of metalloproteins. Curr. Opin. Chem. Biol. 2003, 7, 143–149.
  38. Sinnecker, S.; Neese, F. QM/MM calculations with DFT for taking into account protein effects on the EPR and optical spectra of metalloproteins. Plastocyanin as a case study. J. Comput. Chem. 2006, 27, 1463–1475.
  39. Gleeson, D.; Gleeson, M.P. Application of QM/MM and QM methods to investigate histone deacetylase 8. MedChemComm 2015, 6, 477–485.
  40. Srnec, M.; Ryde, U.; Rulíšek, L. Reductive cleavage of the O–O bond in multicopper oxidases: A QM/MM and QM study. Faraday Discuss. 2011, 148, 41–53.
  41. Senn, H.M.; Thiel, W. QM/MM studies of enzymes. Curr. Opin. Chem. Biol. 2007, 11, 182–187.
  42. Bowman, A.L.; Ridder, L.; Rietjens, I.M.C.M.; Vervoort, J.; Mulholland, A.J. Molecular Determinants of Xenobiotic Metabolism: QM/MM Simulation of the Conversion of 1-Chloro-2,4-dinitrobenzene Catalyzed by M1-1 Glutathione S-Transferase. Biochemistry 2007, 46, 6353–6363.
  43. Khandelwal, A.; Balaz, S. QM/MM linear response method distinguishes ligand affinities for closely related metalloproteins. Proteins: Struct. Funct. Bioinform. 2007, 69, 326–339.
  44. Cho, K.-B.; Derat, E.; Shaik, S. Compound I of Nitric Oxide Synthase: The Active Site Protonation State. J. Am. Chem. Soc. 2007, 129, 3182–3188.
  45. Robertazzi, A.; Platts, J.A. Gas-Phase DNA Oligonucleotide Structures. A QM/MM and Atoms in Molecules Study. J. Phys. Chem. A 2006, 110, 3992–4000.
  46. Sala, D.; Giachetti, A.; Rosato, A. Molecular dynamics simulations of metalloproteins: A folding study of rubredoxin from Pyrococcus furiosus. AIMS Biophys. 2018, 5, 77–96.
  47. Kim, J.; Rees, D.C. Nitrogenase and Biological Nitrogen Fixation. Biochemistry 1994, 33, 389–397.
  48. Hoffman, B.M.; Lukoyanov, D.; Yang, Z.Y.; Dean, D.R.; Seefeldt, L.C. Mechanism of nitrogen fixation by nitrogenase: The next stage. Chem. Rev. 2014, 114, 4041–4062.
  49. Burges, B.K.; Lowe, D.J. Mechanism of Molybdenum Nitrogenase. Chem. Rev. 1996, 96, 2983–3011.
  50. Lawson, D.M.; Smith, B.E. Molybdenum nitrogenases: A crystallographic and mechanistic view. In Metals Ions in Biological System; Sigel, A., Sigel, H., Eds.; CRC Press: Boca Raton, FL, USA, 2002; Volume 39, pp. 75–119.
  51. Brigle, K.E.; Newton, W.E.; Dean, D.R. Complete nucleotide sequence of the Azotobacter vinelandii nitrogenase structural gene cluster. Gene 1985, 37, 37–44.
  52. Bjornsson, R.; Delgado-Jaime, M.U.; Lima, F.A.; Sippel, D.; Schlesier, J.; Weyhermüller, T.; Einsle, O.; Neese, F.; DeBeer, S. Molybdenum L-Edge XAS Spectra of MoFe Nitrogenase. Z. Anorg. Allg. Chem. 2015, 641, 65–71.
  53. Hales, B.J. Vanadium Nitrogenase. Catalysts for Nitrogen Fixation: Nitrogenases, Relevant Chemical Models and Commercial Processes; Springer: Berlin/Heidelberg, Germany, 2004; pp. 255–279. ISBN 978-1-4020-3611-8.
  54. Schneider, K.; Mueller, A. Iron-Only Nitrogenase: Exceptional Catalytic, Structural and Spectroscopic Features. Catalysts for Nitrogen Fixation: Nitrogenases, Relevant Chemical Models and Commercial Processes; Springer: Berlin/Heidelberg, Germany, 2004; pp. 281–307. ISBN 978-1-4020-3611-8.
  55. Igarashi, R.Y.; Seefeldt, L.C. Nitrogen Fixation: The Mechanism of the Mo-Dependent Nitrogenase. Cr. Rev. Biochem. Mol. Biol. 2003, 38, 351–384.
  56. Modak, J.M. Haber Process for Ammonia Synthesis. Resonance 2002, 7, 69–77.
  57. Burgess, B.K. Molybdenum Enzymes (Metal Ions in Biology Series); Spiro, T.G., Ed.; Wiley-Interscience: Hoboken, NJ, USA, 1985; ISBN 978-0471885429.
  58. Simpson, F.B.; Burris, R.H. A nitrogen pressure of 50 atmospheres does not prevent evolution of hydrogen by nitrogenase. Science 1984, 224, 1095–1097.
  59. Yang, Z.Y.; Danyal, K.; Seefeldt, L.C. Mechanism of Mo-Dependent Nitrogenase. Nitrogen Fixation. In Methods in Molecular Biology (Methods and Protocols); Ribbe, M., Ed.; Humana Press: Totowa, NJ, USA, 2011; Volume 766.
  60. Barney, B.M.; Lee, H.I.; Dos Santos, P.C.; Hoffman, B.M.; Dean, D.R.; Seefeldt, L.C. Breaking the N2 triple bond: Insights into the nitrogenase mechanism. DalT Trans. 2006, 19, 2277–2284.
  61. Neese, F. The Yandulov/Schrock cycle and the nitrogenase reaction: Pathways of nitrogen fixation studied by density functional theory. Ang. Chem. 2005, 45, 196–199.
  62. Cao, L.; Ryde, U. Influence of the protein and DFT method on the broken-symmetry and spin states in nitrogenase. Int. J. Quant. Chem. 2018, 118, e25627.
  63. Benediktsson, B.; Bjornsson, R. QM/MM Study of the Nitrogenase MoFe Protein Resting State: Broken-Symmetry States, Protonation States, and QM Region Convergence in the FeMoco Active Site. Inorg. Chem. 2017, 56, 13417–13429.
  64. Spatzal, T.; Aksoyoglu, M.; Zhang, L.; Andrade, S.L.A.; Schleicher, E.; Weber, S.; Rees, D.C.; Einsle, O. Evidence for Interstitial Carbon in Nitrogenase FeMo Cofactor. Science 2011, 334, 940.
  65. Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.; Mittal, J.; Feig, M.; Mackerell, A.D. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ(1) and χ(2) dihedral angles. J. Chem. Theory Comput. 2012, 8, 3257–3273.
  66. Van Stappen, C.; Thorhallsson, A.T.; Decamps, L.; Bjornsson, R.; DeBeer, S. Resolving the structure of the E1 state of Mo nitrogenase through Mo and Fe K-edge EXAFS and QM/MM calculations. Chem. Sci. 2019, 10, 9807–9821.
  67. Thorhallsson, A.T.; Benediktsson, B.; Bjornsson, R. A model for dinitrogen binding in the E4 state of nitrogenase. Chem. Sci. 2019, 10, 11110–11124.
  68. Cao, L.; Caldararu, O.; Ryde, U. Protonation and Reduction of the FeMo Cluster in Nitrogenase Studied by Quantum Mechanics/Molecular Mechanics (QM/MM) Calculations. J. Chem. Theory Comput. 2018, 14, 6653–6678.
  69. Lukoyanov, D.A.; Yang, Z.-Y.; Dean, D.R.; Seefeldt, L.C.; Raugei, S.; Hoffman, B.M. Electron Redistribution within the Nitrogenase Active Site FeMo- Cofactor During Reductive Elimination of H2 to Achieve N≡N Triple-Bond Activation. J. Am. Chem. Soc. 2020, 142, 21679–21690.
  70. Cao, L.; Ryde, U. N2H2 binding to the nitrogenase FeMo cluster studied by QM/MM methods. J. Biol. Inorg. Chem. 2020, 25, 521–540.
  71. Seefeldt, L.C.; Yang, Z.-Y.; Lukoyanov, D.A.; Harris, D.F.; Dean, D.R.; Raugei, S.; Hoffman, B.M. Reduction of Substrates by Nitrogenases. Chem. Rev. 2020, 120, 5082–5106.
  72. Hoffman, B.M.; Lukoyanov, D.; Dean, D.R.; Seefeldt, L.C. Nitrogenase: A draft mechanism. Acc. Chem. Res. 2013, 46, 587–595.
  73. Sgrignani, J.; Franco, D.; Magistrato, A. Theoretical Studies of Homogeneous Catalysts Mimicking Nitrogenase. Molecules 2011, 16, 442–465.
  74. Lukoyanov, D.; Khadka, N.; Yang, Z.Y.; Dean, D.R.; Seefeldt, L.C.; Hoffman, B.M. Reversible Photoinduced Reductive Elimination of H2 from the Nitrogenase Dihydride State, the E4(4H) Janus Intermediate. J. Am. Chem. Soc. 2016, 138, 1320–1327.
  75. Lukoyanov, D.A.; Krzyaniak, M.D.; Dean, D.R.; Wasielewski, M.R.; Seefeldt, L.C.; Hoffman, B.M. Time-Resolved EPR Study of H2 Reductive Elimination from the Photoexcited Nitrogenase Janus E4(4H) Intermediate. J. Phys. Chem. B 2019, 123, 8823–8828.
  76. Lukoyanov, D.; Khadka, N.; Dean, D.R.; Raugei, S.; Seefeldt, L.C.; Hoffman, B.M. Photoinduced Reductive Elimination of H2 from the Nitrogenase Dihydride (Janus) State Involves a FeMo-cofactor-H2 Intermediate. Inorg. Chem. 2017, 56, 2233–2240.
  77. Raugei, S.; Seefeldt, L.C.; Hoffman, B.M. Critical computational analysis illuminates the reductive-elimination mechanism that activates nitrogenase for N2 reduction. Proc. Natl. Acad. Sci. USA 2018, 115, E10521.
  78. Tzeli, D.; Raugei, S.; Xantheas, S.S. Quantitative Account of the Bonding Properties of a Rubredoxin Model Complex q, q = −2, −1, +2, +3. J. Chem. Theory Comput. 2021, 17, 6080–6091.
  79. Mejuto-Zaera, C.; Tzeli, D.; Williams-Young, D.; Tubman, N.M.; Matoušek, M.; Brabec, J.; Veis, L.; Xantheas, S.S.; de Jong, W.A. The Effect of Geometry, Spin and Orbital Optimization in Achieving Accurate, Correlated Results for Iron-Sulfur Cubanes. J. Chem. Theory Comput. 2022. accepted.
  80. Nitrogenase . wikipedia. Retrieved 2022-4-29.
  81. Elghobashi-Meinhardt, N.; Tombolelli, D.; Mroginski, M.A. Electronic and Structural Properties of the Double Cubane Iron-Sulfur Cluster. Catalysts 2021, 11, 245.
  82. Bartlett, R.J. Adventures in DFT by a wavefunction theorist. J. Chem. Phys. 2019, 151, 160901.
  83. Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100.
  84. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789.
  85. Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241.
  86. Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377.
  87. Grimme, S.; Neese, F. Double-hybrid density functional theory for excited electronic states of molecules. J. Chem. Phys. 2007, 127, 154116.
  88. Vydrov, O.A.; Scuseria, G.E. Assessment of a long-range corrected hybrid functional. J. Chem. Phys. 2006, 125, 234109.
  89. Skone, J.H.; Govoni, M.; Galli, G. Nonempirical range-separated hybrid functionals for solids and molecules. Phys. Rev. B 2016, 93, 235106.
  90. Paier, J.; Janesko, B.G.; Henderson, T.M.; Scuseria, G.E.; Grüneis, A.; Kresse, G. Hybrid functionals including random phase approximation correlation and second-order screened exchange. J. Chem. Phys. 2010, 132, 094103.
  91. Zhou, C.; Zhang, Y.; Gong, X.; Ying, F.; Su, P.; Wu, W. Hamiltonian Matrix Correction Based Density Functional Valence Bond Method. J. Chem. Theory Comput. 2017, 13, 627–634.
  92. Henderson, T.M.; Izmaylov, A.F.; Scalmani, G.; Scuseria, G.E. Can short-range hybrids describe long-range-dependent properties? J. Chem. Phys. 2009, 131, 044108.
  93. Yanai, T.; Tew, D.; Handy, N. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57.
  94. Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620.
  95. Yu, H.S.; He, X.; Li, S.L.; Truhlar, D.G. MN15: A Kohn-Sham Global-Hybrid Exchange-Correlation Density Functional with Broad Accuracy for Multi-Reference and Single-Reference Systems and Noncovalent Interactions. Chem. Sci. 2016, 7, 5032–5051.
  96. Elliott, P.; Furche, F.; Burke, K. Excited States from Time-Dependent Density Functional Theory. Rev. Comp. Chem. 2008, 26, 91–165.
  97. Runge, E.; Gross, E.K.U. Density-Functional Theory for Time-Dependent Systems. Phys. Rev. Lett. 1984, 52, 997–1000.
  98. Tao, J.M.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the density functional ladder: Nonempirical meta-generalized gradient approximation designed for molecules and solids. Phys. Rev. Lett. 2003, 91, 146401.
  99. Lingwood, M.; Hammond, J.R.; Hrovat, D.A.; Mayer, J.M.; Thatcher Borden, W. MPW1K Performs Much Better than B3LYP in DFT Calculations on Reactions that Proceed by Proton-Coupled Electron Transfer (PCET). J. Chem. Theory Comput. 2006, 2, 740–745.
  100. Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Insights into Current Limitations of Density Functional Theory. Science 2008, 321, 792–794.
  101. Thiel, W. Semiempirical methods: Current status and perspectives. Tetrahedron 1988, 44, 7393–7408.
  102. Stewart, J.J.P. Semiempirical Molecular orbital methods. Rev. Comput. Chem. 1990, 1, 45–81.
  103. Stewart, J.J.P. MOPAC: A semiempirical molecular orbital program. J. Comp-Aided Mol. Des. 1990, 4, 1–103.
  104. Thiel, W. Perspectives on semiempirical molecular orbital theory. Adv. Chem. Phys. 1996, 93, 703–757.
  105. Clark, T. Quo vadis semiempirical MO theory. J. Mol. Struct. (THEOCHEM) 2000, 530, 1–10.
  106. Thiel, W. Semiempirical methods. In Modern Methods and Algorithms of Quantum Chemistry; Grotendorst, J., Ed.; John von Neumann Institute for Computing: Jülich, Germany, 2000; Volume 3, pp. 261–283. ISBN 3-00-005834-6.
  107. Bredow, T.; Jug, K. Theory and range of modern semiempirical molecular orbital methods. Theor. Chem. Acc. 2005, 113, 1–14.
  108. Koch, W.; Holthausen, M. C. . A Chemist’s Guide to Density Functional Theory; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2001; pp. 1-293.
  109. Nitrogenase . wikipedia. Retrieved 2022-4-29.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Chemistry, Physical
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Christina Tzeliou
,
Markella Mermigki
,
Demeter Tzeli
View Times: 1.4K
Entry Collection: Chemical Bond
Revisions: 5 times (View History)
Update Date: 05 May 2022
Table of Contents
    1000/1000
    Hot Most Recent
    Video Production Service
    Feedback