Your browser does not fully support modern features. Please upgrade for a smoother experience.

Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic.
For video creation, please contact our Academic Video Service.
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | David Simeone | -- | 1928 | 2022-04-29 14:22:39 | | | |
| 2 | Camila Xu | + 15 word(s) | 1943 | 2022-05-05 05:20:28 | | |
Video Upload Options
We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Simeone, D.; Luneville, L.; , . The Phase Field Approach. Encyclopedia. Available online: https://encyclopedia.pub/entry/22504 (accessed on 11 January 2026).
Simeone D, Luneville L, . The Phase Field Approach. Encyclopedia. Available at: https://encyclopedia.pub/entry/22504. Accessed January 11, 2026.
Simeone, David, Laurence Luneville, . "The Phase Field Approach" Encyclopedia, https://encyclopedia.pub/entry/22504 (accessed January 11, 2026).
Simeone, D., Luneville, L., & , . (2022, April 29). The Phase Field Approach. In Encyclopedia. https://encyclopedia.pub/entry/22504
Simeone, David, et al. "The Phase Field Approach." Encyclopedia. Web. 29 April, 2022.
Copy Citation
The phase field approach was developed in the last 20 years to handle radiation damage in materials. This approach bridges the gap between atomistic simulations extensively used to model first step of radiation damage at short time and continuum approach at large time. The main advantage of such an approach lies in its ability to compute not only the microstructure at the nanometric scale but also to calculate generalized susceptibilities such as elastic constants under irradiation.
radiation-induced patterning
phase field approach
nano-structures
1. Introduction
Modern materials science has enormously progressed from a descriptive endeavor to more physically sounded foundations. The ultimate goal of such a fundamental tilt is to design material with tunable properties. The use of new experimental techniques such as particle irradiation made possible to escape the tyranny of the phase diagram. Overcoming this restriction, it becomes possible to observe the formation of patterns at the nanometric scale. It is now clear that such patterns affect the properties of materials and thus need to be understood and controlled.
On the other hand, materials under irradiation may be considered as toy models to study systems maintained far from equilibrium. Varying the control parameters (temperature, particles flux), experimentalists can then test different approaches for modeling instabilities and pattern formation far from equilibrium.
The slowing down of energetic particles (electrons, ions and neutron) in crystalline solids were studied in detail over the past 60 years [1]. Even if mechanisms occurring during the slowing down of particles are complex [2], it is nowadays admitted that a part of the energy dissipated by incident particles during their slowing down generates a distribution of point and extended defects in materials. This distribution is far from being uniformly distributed along the material but localized in spatial areas, named displacement cascades [3]. The atomic fraction of defects in these areas is largely superior to those expected from the thermal equilibrium. Such an over-concentration of defects is responsible for the formation of unexpected microstructures over few tens of nanometers: voids, bubbles and nano-precipitates. Moreover, self-organized nano-structures may emerge under some specific conditions of irradiation flux and temperature. Many examples of such patterns have been observed in metals, alloys, ceramics and amorphous materials [3][4][5][6][7].
2. The Phase Field Approach
The main difficulties of the rate theory is due to the fact that many parameters are needed to efficiency model the large time microstructure such as the strength of sinks k∗ for instance. These parameters evolve with the microstructure via elastic (or electric for ceramics) interactions leading to a feed back effect difficult to understand.
On the other hand, the spatial distribution of sub cascades responsible for the anisotropy of the point defects production terms are difficult to take into account in such a formalism. Kinetic Monte Carlo methods were then developed handling the spatial anisotropy of the defects formation. However, the accuracy of these simulations is directly related to the knowledge of main defects produced under irradiation and their associated diffusion paths. Up to now, no clear formalism such as for instance the detailed balance in thermal equilibrium exists under irradiation, assessing the validity of the choice of the set of defects and their diffusion paths.
During the last decade, the phase field approaches initially developed by Landau [8] for describing phase transition in thermal equilibrium, has been successfully applied for understanding and modeling radiation-induced nano-patterns. This approach seems to reproduce kinetic Monte Carlo simulations and offers a guide to understand key parameters responsible for the nano-structures induced by irradiation. On the other hand, this approach provides the unique opportunity to compute generalized susceptibilities (elastic constants, dielectric constants, etc.) associated with radiation-induced nano-structures. Researchers briefly describe the application of the phase field to radiation-induced patterning.
Foundation of the Phase Field
As it is the case for the rate theory, the phase field may be understood as a mean field theory. To understand this, researchers can assume that an atom in a disordered solid occupies a vertex of a geometric lattice, assumed cubic for simplicity. At the atomic scale, all sites of the underlying lattice are occupied by species (atoms or vacancy). Calling σi the occupation number at the i -th site and d the dimension of the lattice defined by a characteristic length a, researchers can define “d-blocks”. Every “d-block” will have a volume lad. Researchers can define the averaged occupation σ(r) by a coarse-graining procedure:

(1)
Nl can be understood as the number of degrees of freedom. Obviously, different coarse-graining procedures can be used instead of a simple summation. However, this definition seems reasonable as long as Nl is large. After performing an averaging, σl(r) does not fluctuate much on microscopic scale but varies smoothly in space.
Of course, in general researchers need to specify l in order to determine σl(r), but the coarse graining procedure researchers are applying will be useful only if the final results are independent of l at least in the spatial scales considered. Under equilibrium, researchers now must express the partition function in terms of Heff(σl(r)), where Heffcan be considered as an effective Hamiltonian [9]. Since researchers now have a system made up of “blocks” this effective Hamiltonian will be composed of two parts: a bulk component relative to the single blocks and an interface component relative to the interactions between the blocks.
When researchers suppose that every block of volume lad is separated from the rest of the system, σl(r) inside every one of them is uniform only if the dimension of the blocks is much smaller than the correlation length, i.e., the characteristic length of variation of σl(r) labeled ξ. When la<<ξ, a non equilibrium free energy density f(σ(r)) may be introduced according to Landau [10][11]. This free energy density, f(r), describes the evolution of a uniform system made of non interacting blocks. The coarse graining procedure insures that σl(r) results from a mean field theory.
To go a step beyond, researchers now must take into account the fact that adjacent blocks do interact. Since, as researchers have stated, σl(r) does not vary much on microscopic scales, the interactions between the blocks must be such that strong variations of magnetization between neighboring blocks are energetically unfavorable. If researchers call δl a vector of magnitude la that points from one block to a neighboring one, the most simple analytic expression that researchers can guess for such a term can be an harmonic one:
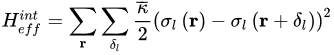
(2)
where the factor 1/2 multiplying κ¯ has been inserted for convenience. The term κ¯ defines the stiffness of the material under consideration, i.e., the ability of the material to create interfaces between blocks.
This term known as the Ginzburg term [8][11] can also be considered as a first approximation of a general interaction between the blocks, namely as the first terms of a Taylor expansion of the real interaction energy. Since the linear dimension of the blocks la is much smaller than the characteristic length L of the system, researchers can treat r as a continuous variable and thus substitute the sum over r with an integral:
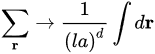
(3)
Finally, researchers obtain the following expression for the Hamiltonian:
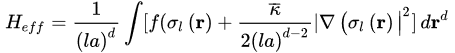
(4)
Application of the saddle point approximation allows computing the partition function Z(β) and allows identifying F=−kBTlog(Z) to the stationary value σ(r) of the functional Heff. The term |∇(σl(r)|2 insures that the Ginzburg–Landau free energy F may take into account inhomogeneities of the order parameter σ(r)[10][11]. The term κ=κ¯/2(la)d−2 is the cost associated with the formation of an interface. The Landau free energy describes the evolution of the system not only at equilibrium but also far from equilibrium. It must be kept in mind that the non equilibrium Landau free energy exhibits some minima corresponding to those associated with phase diagrams expected from equilibrium. As the free energy is not restricted to the equilibrium free energy, such an approach allows computing a kinetic path for the transition. As it is the case for the rate theory, application of the PF approach to radiation damage may allow computing radiation-induced microstructures.
The kinetics of the system is now given by a partial differential equation:
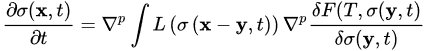
(5)
L(σ(x,t) is the Onsager coefficient associated with the kinetic path [13]. This kinetic coefficient defines the relaxation time scale. From the definition of the order parameter (atomic position, atomic fraction, polarization, strain field, etc.) and the non equilibrium free energy, more generally thermodynamic potential, it is possible from Equation (5) to infer some features of the system: list of all possible low symmetry phases for a given symmetry of the “parent” phase, degeneracy of the “low symmetry” phases (number of variants) and susceptibilities (latent heat, heat capacity, etc.). In Equation (5), δF(T,σ(x,t)/δσ(y,t) has a clear meaning. It is the chemical potential of the system. Kinetics occurring during a lower time scale cannot be handle by such relaxation equations. For non conservative OP [12], p is null. It is equal to 1 for conservative OP [14]. Neglecting the dependence of Onsager coefficient with the OP, classical PF equations are recovered [15]:
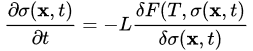
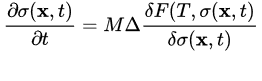
(6)(7)
The first equation holds for non conservative OP associated with ordering whereas the second equation holds for conservative OP associated with phase separation. L can be understood as a damping coefficient controlling the time relaxation of the OP to its equilibrium value. Usually, the term M is the mobility and is related to the diffusion coefficient of diffusing species. Introducing the H−1 inner product defined by <f|g>H−1=<(−Δ)−1f|g>L2 for functions of L2(Rd) (d is the dimension of the embedded space), the two equations are formally identical. Both dynamics are then gradient flows of the same Lyapunov functional, L[σ],associated with the H−1 or the L2 metrics. Computing the inner product in the Sobolev space H−1 is equivalent to solve the Poisson equation Δw=−f associated with boundary conditions.
Equation (8) may be derived from the application of the principle of minimal energy dissipation postulated by Onsager [16]. This principle is based on the assumption that the system under consideration is close to an equilibrium condition, so that locally thermodynamic equilibrium can be assumed. As a consequence the concepts of equilibrium thermodynamics can be extended to these non-equilibrium conditions based on the linearization of different fluxes as a function of the generalized thermodynamic forces.

(8)
Assuming kinetic coefficients L and M do not depend on the order parameter, Equation (8) is a gradient systems and F(T,σ(r,t) is the Lyapunov of the system [17] and dF/dt<0. This implies that dynamics evolves to different minima of F(T,σ(r,t). As it is the case for the rate theory, different minima of F(T,σ(r,t) define a set of different attractors of the system. These attractors are separated by separatrices. These separatrices themselves make up an invariant set for the gradient flow dynamics. These gradient systems are dissipative systems since dF/dt<0 even when M and L are assumed independent of the order parameter.
These partial differential equations can be solve as soon as boundary and initial conditions are defined:
-
The initial condition is usually given by an uniform distribution σ¯ of the order parameter in the integration volume V. Since σ¯ is an attractor of these equations, a small random variable db is added to the uniform value of the order parameter. The mean value of this random variable db is null and its variance of the order of kBT [18].
-
For close systems, Neumann conditions must be applied to the the order parameter and the driving force, defined by the chemical potential ∂L[σ]/∂σ(x,t). This implies ∇σ ad ∇3σ are null over δV for the conservative Cahn–Hilliard equation. Obviously for the non conservative equation, only the second condition holds.
-
Neglecting edge effects, periodic conditions are usually applied for computing microstructures within the framework of the phase field theory. This implies that the order parameter σ(x,t) can be expanded in an infinite cosine set. Numerically, a finite set of discrete cosine transform (dct-I) is used to solve these equations for close systems [19].
References
- Sigmund, P. Particle Radiation and Radiation Effects; Springer Series in Solid State Sciences; Springer: Berlin/Heidelberg, Germany, 2006; Volume 151.
- Simeone, D.; Ribis, J.; Luneville, L. Continuum approaches for modeling radiation-induced self-organization in materials: From the rate theory to the phase field approach. J. Mat. Res. 2018, 33, 440–454.
- Simeone, D.; Demange, G.; Luneville, L. Disrupted coarsening in complex Cahn-Hilliard dynamics. Phys. Rev. E 2013, 88, 032116.
- Enrique, R.A.; Bellon, P. Self organized Cu-Ag nanocomposites synthesized by intermediate temperature ion-beam mixing. Appl. Phys. Lett. 2001, 78, 4178.
- Ghoniem, N.; Walgraef, D. Instabilities and Self Organization in Materials; Oxford Science Publications: Oxford, UK, 2008; Volume I.
- Baldinozzi, G.; Simeone, D.; Gosset, D.; Monnet, I.; Le Caër, S.; Mazerolles, L. Evidence of extended defects in pure zirconia irradiated by swift heavy ions. Phys. Rev. B 2006, 74, 132107.
- Beauford, M.; Vallet, M.; Nicolai, J.; Bardot, J. In situ evolution of He bubbles in SiC under irradiation. J. Appl. Phys. 2015, 118, 205904.
- Landau, L.; Lifchitz, L. Theoretical Physics; MIR: Moscow, Russia, 1975; Volume 4.
- Le Bellac, M.; Mortessagne, F.; Batrouni, G. Equilibrium and Non Equilibrium Statistical Thermodynamics; Cambridge University Press: Cambridge, UK, 2010.
- Ginzburg, V.L.; Landau, L.D. On the Theory of Superconductivity. Sov. Phys. JETP 1950, 20, 1064.
- Tolédano, P.; Dmitriev, V. Reconstructive Phase Transitions: In Crystals and Quasicrystals; World Scientific: Singapore, 1996.
- Ginzburg, V.L.; Landau, L.D. On the Theory of Superconductivity. Sov. Phys. JETP 1950, 20, 1064.
- Khatchaturyan, A.G. Theory of Structural Transformation in Solids; Wiley Interscience: Hoboken, NJ, USA, 1983.
- Cahn, J.W. On Spinodal Decomposition. Acta Metall. 1961, 9, 795.
- Hohenberg, P.C.; Halperin, B.I. Theory of dynamic critical phenomena. Rev. Mod. Phys. 1977, 49, 435–479.
- Khatchaturyan, A.G. Theory of Structural Transformation in Solids; Wiley Interscience: Hoboken, NJ, USA, 1983.
- Cahn, J.W. On Spinodal Decomposition. Acta Metall. 1961, 9, 795.
- Hohenberg, P.C.; Halperin, B.I. Theory of dynamic critical phenomena. Rev. Mod. Phys. 1977, 49, 435–479.
- Onsager, L. Reciprocal Relations in Irreversible Processes I. Phys. Rev. 1931, 37, 405–410.
- Khatchaturyan, A.G. Theory of Structural Transformation in Solids; Wiley Interscience: Hoboken, NJ, USA, 1983.
- Cahn, J.W. On Spinodal Decomposition. Acta Metall. 1961, 9, 795.
- Hohenberg, P.C.; Halperin, B.I. Theory of dynamic critical phenomena. Rev. Mod. Phys. 1977, 49, 435–479.
More
Information
Subjects:
Physics, Condensed Matter
Contributors
MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register
:
View Times:
995
Revisions:
2 times
(View History)
Update Date:
05 May 2022
Notice
You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
OK
Confirm
Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
Yes
No
${ textCharacter }/${ maxCharacter }
Submit
Cancel
Back
Comments
${ item }
|
More
No more~
There is no comment~
${ textCharacter }/${ maxCharacter }
Submit
Cancel
${ selectedItem.replyTextCharacter }/${ selectedItem.replyMaxCharacter }
Submit
Cancel
Confirm
Are you sure to Delete?
Yes
No




