Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1 By emulating the human brain, neuromorphic computing appears as a promising approach to allow for high energy efficiency and low latency in artificial intelligence. The adoption of nonvolatile memories with unique physical properties might enable neuromor
Daniele Ielmini
 + 982 word(s) 982 2020-01-07 04:52:13 |
2 format change
Nicole Yin
 -3 word(s) 979 2020-07-31 07:43:06 | |
3 format change
Nicole Yin
 -1 word(s) 978 2020-10-23 03:46:43 |

Video Upload Options

We provide professional Video Production Services to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Milo, V.; Malavena, G.; Monzio Compagnoni, C.; Ielmini, D. Neuromorphic Computing. Encyclopedia. Available online: https://encyclopedia.pub/entry/224 (accessed on 16 November 2024).
Milo V, Malavena G, Monzio Compagnoni C, Ielmini D. Neuromorphic Computing. Encyclopedia. Available at: https://encyclopedia.pub/entry/224. Accessed November 16, 2024.
Milo, Valerio, Gerardo Malavena, Christian Monzio Compagnoni, Daniele Ielmini. "Neuromorphic Computing" Encyclopedia, https://encyclopedia.pub/entry/224 (accessed November 16, 2024).
Milo, V., Malavena, G., Monzio Compagnoni, C., & Ielmini, D. (2020, January 10). Neuromorphic Computing. In Encyclopedia. https://encyclopedia.pub/entry/224
Milo, Valerio, et al. "Neuromorphic Computing." Encyclopedia. Web. 10 January, 2020.
Neuromorphic Computing
Edit
This entry is adapted from the peer-reviewed paper 10.3390/ma13010166

Neuromorphic computing systems aims at processing information in a way similar to the human brain. Instead of a conventional von Neumann computer, a neuromorphic system generally relies on a neural network, where the memory and the processing elements are intimately co-located within the same hardware. Neuromorphic computing takes advantage of computational memories, which can both store and process data via physical laws within the device and/or the circuit. This entry summarizes the history and main concepts of neuromorphic computing, including both deep neural networks (DNNs) which are adopted for extensive artificial intelligence tasks, such as driverless cars, and spiking neural networks (SNNs), which aim at a more realistic brain-inspired computation. 

Neural networks artificial synapses nonvolatile memory deep learning spiking neural network

1. Introduction

The origin of neuromorphic computing can be traced back to 1949, when McCulloch and Pitts proposed a mathematical model of the biological neuron. This is depicted in Figure 1a, where the neuron is conceived as a processing unit, operating (i) a summation of input signals (x1, x2, x3, …), each multiplied by a suitable synaptic weight (w1, w2, w3, …) and (ii) a non-linear transformation according to an activation function, e.g., a sigmoidal function[1]. A second landmark came in 1957, when Rosenblatt developed the model of a fundamental neural network called multiple-layer perceptron (MLP)[2], which is schematically illustrated in Figure 1b. The MLP consists of an input layer, one or more intermediate layers called hidden layers, and an output layer, through which the input signal is forward propagated toward the output. The MLP model constitutes the backbone for the emerging concept of deep neural networks (DNNs). DNNs have recently shown excellent performance in tasks, such as pattern classification and speech recognition, via extensive supervised training techniques, such as the backpropagation rule[3][4][5]. DNNs are usually implemented in hardware with von Neumann platforms, such as the graphics processing unit (GPU)[6] and the tensor processing unit (TPU)[7], used to execute both training and inference. These hardware implementations, however, reveal all the typical limitations of the von Neumann architecture, chiefly the large energy consumption in contrast with the human brain model.

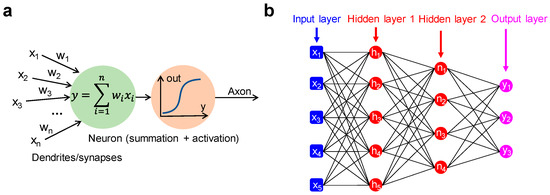
Materials 13 00166 g001 550

Figure 1. (a) Conceptual illustration of McCulloch and Pitts artificial neuron architecture, where the weighted sum of the input signals is subject to the application of a non-linear activation function yielding the output signal. (b) Schematic representation of a multilayer perceptron consisting of two hidden layers between the input and the output layer.

To significantly improve the energy efficiency of DNNs, matrix-vector multiplication (MVM) in crossbar memory arrays has emerged as a promising approach[8][9]. Memory devices also enable the implementation of learning schemes able to replicate the biological synaptic plasticity at the device level. CMOS memories, such as the static random access memory (SRAM)[10][11] and the Flash memory[12], were initially adopted to capture synaptic behaviors in hardware. In the last 10 years, novel material-based memory devices, generically referred to as memristors[13], have evidenced attractive features for the implementation of neuromorphic hardware, including non-volatile storage, low-power operation, nanoscale size, and analog resistance tunability. In particular, memristive technologies, which include resistive switching random access memory (RRAM), phase change memory (PCM), and other emergent memory concepts based on ferroelectric and ferromagnetic effects, have been shown to achieve synapse and neuron functions, enabling the demonstration of fundamental cognitive primitives as pattern recognition in neuromorphic networks[14][15][16][17].

2. The Field of Neuromorphic Networks

The field of neuromorphic networks includes both the DNN[18], and the spiking neural network (SNN), the latter more directly inspired by the human brain[19]. Contrary to DNNs, the learning ability in SNNs emerges via unsupervised training processes, where synapses are potentiated or depressed by bio-realistic learning rules inspired by the brain. Among these local learning rules, spike-timing-dependent plasticity (STDP) and spike-rate-dependent plasticity (SRDP) have received intense investigation for hardware implementation of brain-inspired SNNs. In STDP, which was experimentally demonstrated in hippocampal cultures by Bi and Poo in 1998[20], the synaptic weight update depends on the relative timing between the pre-synaptic spike and the post-synaptic spike (Figure 2a). In particular, if the pre-synaptic neuron (PRE) spike precedes the post-synaptic neuron (POST) spike, namely the relative delay of spikes, Δt = tpost − tpre, is positive, then the interaction between the two spikes causes the synapse to increase its weight, which goes under the name of synaptic potentiation. On the other hand, if the PRE spike follows the POST spike, i.e., Δt is negative, then the synapse undergoes a weight decrease or synaptic depression (Figure 2b). In SRDP, instead, the rate of spikes emitted by externally stimulated neurons dictates the potentiation or depression of the synapse, with high and low frequency stimulation leading to synaptic potentiation and depression, respectively[21]. Unlike STDP relying on pairs of spikes, SRDP has been attributed to the complex combination of three spikes (triplet) or more[22][23][24][25]. In addition to the ability to learn in an unsupervised way and emulate biological processes, SNNs also offer a significant improvement in energy efficiency thanks to the ability to process data by transmission of short spikes, hence consuming power only when and where the spike occurs[26]. Therefore, CMOS and memristive concepts can offer great advantages in the implementation of both DNNs and SNNs, providing a wide portfolio of functionalities, such as non-volatile weight storage, high scalability, energy efficient in-memory computing via MVM, and online weight adaptation in response to external stimuli.

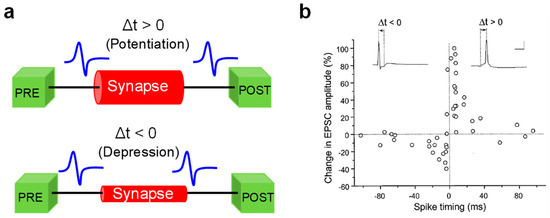
Materials 13 00166 g002 550

Figure 2. (a) Sketch of the spike-timing-dependent plasticity (STDP) learning rule. If the PRE spike arrives just before the POST spike at the synaptic terminal (Δt > 0), the synapse undergoes a potentiation process, resulting in a weight (conductance) increase (top). Otherwise, if the PRE spike arrives just after the POST spike (Δt < 0), the synapse undergoes a depression process, resulting in a weight (conductance) decrease (bottom). (b) Relative change of synaptic weight as a function of the relative time delay between PRE and POST spikes measured in hippocampal synapses by Bi and Poo. Reprinted with permission from[20]. Copyright 1998 Society for Neuroscience.

References

  1. Warren S. McCulloch; Walter Pitts; A logical calculus of the ideas immanent in nervous activity. Bulletin of Mathematical Biology 1943, 5, 115-133, 10.1007/bf02478259.
  2. Rosenblatt, F. The Perceptron: A Perceiving and Recognizing Automaton Project Para; Report 85-460-1; Cornell Aeronautical Laboratory: Buffalo, NY, USA, 1957.
  3. Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representation by backpropagating errors. Nature 1986, 323, 533–536.
  4. LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324.
  5. LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444.
  6. Coates, A.; Huval, B.; Wang, T.; Wu, D.; Ng, A.Y.; Catanzaro, B.C. Deep learning with COTS HPC systems. In Proceedings of the 30th International Conference on Machine Learning (ICML), Atlanta, GA, USA, 16–21 June 2013; Volume 28, pp. 1337–1345.
  7. Jouppi, N.P.; Young, C.; Patil, N.; Patterson, D.; Agrawal, G.; Bajwa, R.; Bates, S.; Bathia, S.; Boden, N.; Borchers, A.; et al. In-Datacenter performance analysis of a Tensor Processing UnitTM. In Proceedings of the 44th International Symposium on Computer Architecture (ISCA), Toronto, ON, Canada, 24–28 June 2017; pp. 1–12.
  8. Hu, M.; Graves, C.E.; Li, C.; Li, Y.; Ge, N.; Montgomery, E.; Davila, N.; Jiang, H.; Williams, R.S.; Yang, J.J.; et al. Memristor-based analog computation and neural network classification with a dot product engine. Adv. Mater. 2018, 30, 1705914.
  9. Xia, Q.; Yang, J.J. Memristive crossbar arrays for brain-inspired computing. Nat. Mater. 2019, 18, 309–323.
  10. Merolla, P.A.; Arthur, J.V.; Alvarez-Icaza, R.; Cassidy, A.S.; Sawada, J.; Akopyan, F.; Jackson, B.L.; Imam, N.; Guo, C.; Nakamura, Y.; et al. A million spiking-neuron integrated circuit with a scalable communication network and interface. Science 2014, 345, 668–673.
  11. Moradi, S.; Qiao, N.; Stefanini, F.; Indiveri, G. A scalable multicore architecture with heterogeneous memory structures for dynamic neuromorphic asynchronous processors (DYNAPs). IEEE Trans. Biomed. Circuits Syst. 2017, 12, 106–122.
  12. Shubha Ramakrishnan; Paul E. Hasler; Christal Gordon; Floating Gate Synapses With Spike-Time-Dependent Plasticity. IEEE Transactions on Biomedical Circuits and Systems 2011, 5, 244-252, 10.1109/TBCAS.2011.2109000.
  13. Dmitri B. Strukov; Gregory S. Snider; Duncan R. Stewart; R. Stanley Williams; The missing memristor found. Nature 2008, 453, 80-83, 10.1038/nature06932.
  14. Kuzum, D.; Yu, S.; Wong, H.-S.P. Synaptic electronics: Materials, devices and applications. Nanotechnology 2013, 24, 382001.
  15. Burr, G.W.; Shelby, R.M.; Sebastian, A.; Kim, S.; Kim, S.; Sidler, S.; Virwani, K.; Ishii, M.; Narayanan, P.; Fumarola, A.; et al. Neuromorphic computing using non-volatile memory. Adv. Phys. X 2017, 2, 89–124.
  16. Yu, S. Neuro-inspired computing with emerging nonvolatile memory. Proc. IEEE 2018, 106, 260–285.
  17. Ielmini, D.; Ambrogio, S. Emerging neuromorphic devices. Nanotechnology 2020, 31, 092001.
  18. Vivienne Sze; Yu-Hsin Chen; Tien-Ju Yang; Joel S. Emer; Efficient Processing of Deep Neural Networks: A Tutorial and Survey. Proceedings of the IEEE 2017, 105, 2295-2329, 10.1109/jproc.2017.2761740.
  19. Wolfgang Maass; Networks of spiking neurons: The third generation of neural network models. Neural Networks 1997, 10, 1659-1671, 10.1016/s0893-6080(97)00011-7.
  20. Guo-Qiang Bi; Mu-Ming Poo; Synaptic Modifications in Cultured Hippocampal Neurons: Dependence on Spike Timing, Synaptic Strength, and Postsynaptic Cell Type. The Journal of Neuroscience 1998, 18, 10464-10472, 10.1523/JNEUROSCI.18-24-10464.1998.
  21. Per Jesper Sjöström; Gina G Turrigiano; S B Nelson; Rate, Timing, and Cooperativity Jointly Determine Cortical Synaptic Plasticity. Neuron 2001, 32, 1149-1164, 10.1016/s0896-6273(01)00542-6.
  22. Gjorgjieva, J.; Clopath, C.; Audet, J.; Pfister, J.P. A triplet spike timing dependent plasticity model generalizes the Bienenstock-Cooper-Munro rule to higher-order spatiotemporal correlations. Proc. Natl. Acad. Sci. USA 2011, 108, 19383–19388.
  23. Pfister, J.-P.; Gerstner, W. Triplets of spikes in a model of spike timing-dependent plasticity. J. Neurosci. 2006, 26, 9673–9682.
  24. Rachmuth, G.; Shouval, H.-Z.; Bear, M.F.; Poon, C.-S. A biophysically-based neuromorphic model of spike rate- and timing-dependent plasticity. Proc. Natl. Acad. Sci. USA 2011, 108, E1266–E1274.
  25. Milo, V.; Pedretti, G.; Carboni, R.; Calderoni, A.; Ramaswamy, N.; Ambrogio, S.; Ielmini, D. A 4-Transistors/1-Resistor hybrid synapse based on resistive switching memory (RRAM) capable of spike-rate-dependent plasticity (SRDP). IEEE Trans. Very Large Scale Integrat. (VLSI) Syst. 2018, 26, 2806–2815.
  26. Giacomo Indiveri; Shih-Chii Liu; Indiveri G.; Memory and Information Processing in Neuromorphic Systems. Proceedings of the IEEE 2015, 103, 1379-1397, 10.1109/jproc.2015.2444094.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Nanoscience & Nanotechnology; Engineering, Electrical & Electronic
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Valerio Milo
,
Gerardo Malavena
,
Christian Monzio Compagnoni
,
Daniele Ielmini
View Times: 2.7K
Revisions: 3 times (View History)
Update Date: 22 Jan 2021
Table of Contents
    1000/1000
    Hot Most Recent
    ScholarVision Creations
    Feedback