You're using an outdated browser. Please upgrade to a modern browser for the best experience.
Submitted Successfully!
Thank you for your contribution! You can also upload a video entry or images related to this topic. For video creation, please contact our Academic Video Service.
Version Summary Created by Modification Content Size Created at Operation
1 Kadir Gunaydin + 3104 word(s) 3104 2022-02-23 03:51:48 |
2 format Bruce Ren + 1 word(s) 3105 2022-02-28 03:11:08 |

Video Upload Options

We provide professional Academic Video Service to translate complex research into visually appealing presentations. Would you like to try it?
No, upload directly Yes

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Gunaydin, K. Production and Characterization of Additively Manufactured Chiral Elements. Encyclopedia. Available online: https://encyclopedia.pub/entry/19914 (accessed on 05 December 2025).
Gunaydin K. Production and Characterization of Additively Manufactured Chiral Elements. Encyclopedia. Available at: https://encyclopedia.pub/entry/19914. Accessed December 05, 2025.
Gunaydin, Kadir. "Production and Characterization of Additively Manufactured Chiral Elements" Encyclopedia, https://encyclopedia.pub/entry/19914 (accessed December 05, 2025).
Gunaydin, K. (2022, February 25). Production and Characterization of Additively Manufactured Chiral Elements. In Encyclopedia. https://encyclopedia.pub/entry/19914
Gunaydin, Kadir. "Production and Characterization of Additively Manufactured Chiral Elements." Encyclopedia. Web. 25 February, 2022.
Production and Characterization of Additively Manufactured Chiral Elements
Edit
This entry is adapted from the peer-reviewed paper 10.3390/ma15041520

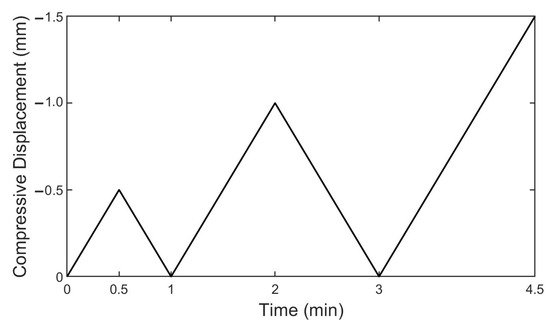
For material characterization and understanding the material behavior of EBM printed parts, tensile and three-point flexural tests are conducted. Log signals produced during the EBM process are investigated to confirm the stability of the process and the health of the produced parts. Furthermore, a compressive cyclic load profile is applied to the EBM printed chiral units having two different thicknesses to track their Poisson's ratios and displacement limits under large displacements without the formation of degradation, permanent deformations and failures. Chiral units are also crushed to investigate the effect of failure and deformation mechanisms on the energy absorption characteristics. Moreover, a surface roughness study is conducted due to the high surface roughness of EBM printed parts and an equation is offered to define load-carrying effective areas to prevent misleading cross-section measurements. In compliance with the equation and tensile test results, a constitutive equation is formed and used after a selection and calibration process to verify the numerical model for optimum topology design and mechanical performance forecasting using a non-linear computational model with failure analysis. As a result, the cyclic compression and crush numerical analyses of EBM printed Ti6Al4V chiral cells are validated with the experimental results. It is shown that the constitutive equation of EBM printed as-built parts is extracted accurately considering the build orientation and surface roughness profile. Besides, the cyclic compressive and crush behavior of chiral units are investigated. The regions of the chiral units prone to prematurely fail under crush loads are determined and deformation modes are investigated to increase the energy absorption abilities.

additive manufacturing EBM auxetic chiral energy absorption FEM

1. Introduction

Lightweight structures such as sandwich structures play a crucial role in aviation, automotive and military applications, due to the importance of crush and compression strength at impact and blast conditions. Various types of sandwich structures having different types of cores, for instance, lattices, foams and trusses, have been proposed for crashworthy structures. In terms of crashworthiness, the lattice cores have come to the fore, and auxetic solid cellular structures are among the most promising types of lattice structures studied in recent years [1]. Auxetic lattice solid structures reach a negative Poisson’s ratio by showing a significantly different behavior from conventional materials: shrinkage under a compressive load and expansion under a tensile load.
The term auxetic was initially offered by Evans [1] in the year 1991 after Lake [2] introduced the first known synthetic foam structured material with a negative Poisson’s ratio (NPR). NPR materials also can be termed metamaterials, since they are engineered from conventional materials by adopting specific topologies [3][4][5][6]. Indeed, Poisson’s ratios of a chiral auxetic lattice structure is a topological specification that is independent of the structure’s material according to the theoretical approach if the material is isotropic [7]. The special properties of auxetic structures can be obtained through topological configurations. Adjusting different specifications can be done by modification of the unit cell, which is the smallest repetitive domain of the lattice network. At the metamaterial level, mechanical properties such as Young’s Modulus, Poisson’s ratio, sound absorption coefficient and the coefficient of thermal expansion can be adjusted by tailoring the unit cell. In addition, auxetic materials have some special properties, such as high global flexibility without strain localization, improved fracture toughness, transverse shear moduli and most importantly, indentation resistance [8]. Moreover, auxetic lattices can be formed as doubly curved and dome shaped structures. Due to the listed highly remarkable specifications, auxetic structures have been exploited in several applications in aerospace, automotive and defense industries [9][10][11][12]. Different types of auxetic lattice cells can be found in the literature [13][14][15][16].
Among the auxetic lattice structures, chiral lattice structures are one of the most known auxetic lattice structures experiencing a Poisson’s ratio of −1. The structural chiral auxetic honeycomb concept was initially proposed by Prall and Lakes, and the Poisson’s ratio of −1 was proven in a theoretical way based on standard beam theory in their study [7]. Due to its non-centrosymmetric topology, chiral cellular solids exhibit anisotropic behavior, and auxeticity occurs in the edgewise direction (in-plane), so research on it can be divided into two classes, which are edgewise and flat (out-of-plane) studies. Spadoni et al. [17] investigated global linear buckling behavior numerically in the flatwise direction; an FEM model was used in this study with classical theoretical equations for buckling of shells and thin plates while considering the possible formation of localized plasticity. Lorato et al. [18] developed analytical and FEM models to calculate the flatwise Young’s moduli and shear stiffness values of trichiral, tetrachiral and hexachiral lattice configurations, and the models were validated with experimental results. A flatwise dynamic compression study was conducted by Lu et al. [19] to investigate energy absorption behavior, and novel hierarchical chiral lattice elements were presented and adjusted to reach special structures with better energy absorption capabilities.
A number of edgewise studies have been conducted, one of which involved a mathematical model using dynamic shape functions to explain dynamic behavior over a broad frequency range [20]. Additionally, several studies have been conducted on the wave propagation characterization of chiral structures [21][22][23][24]. Chiral structures can maintain their auxeticity under large overall displacement within the elastic deformation limits; however, when they are subjected to large deformations causing plastic deformation, their auxeticity deceives. Zhu et al. [25] used wavy ligaments in their study to increase the auxeticity limit of chiral cells for large elasto-plastic deformation, and as a result, the new structure experienced better performance. Another auxeticity study was conducted by Alderson et al. [3] to elaborate on the elastic properties and auxetic behavior of different chiral cells having 3, 4 or 6 ligaments connected to one node. Additionally, a numerical and experimental study was performed to investigate the elastic and yield onset behavior of achiral and chiral lattice structures, both having six-fold rotational symmetry, in 2D [26]. Furthermore, homogenization studies were conducted for chiral lattices to obtain computationally low cost models [4][27][28]. Despite the peculiar properties of auxetic metamaterials that depend on the topologies adopted, the material of the cellular structures is important in the determination of the mechanical performance for mechanical properties and energy absorption capabilities. Moreover, the production method indirectly plays an important role in cost, production challenges and efficiency. Commercial production of metal-based honeycomb structures includes cutting and bending of aluminum sheet rolls [29]. The advancements in the processes of additive manufacturing (AM) in the past few years have offered the opportunity to generate arbitrary typologies with fewer constraints compared to conventional methods of production. One of the important AM approaches is EBM additive manufacturing, which is using an electron beam to melt and to fuse metallic powders [30]. To sum up, several studies on chiral auxetics have been conducted. However, to the authors’ knowledge, there have been no studies on metal chiral cellular solids and their cyclic and crush performances, along with failure analysis. To fill in that gap and investigate the performance of EBM printed chiral auxetics via failure analysis, this study was performed.

2. Production and Characterization of Additively Manufactured Chiral Elements

2.1. Chiral Cellular Structures

A chiral auxetic solid network can be described by its interconnected nodes and ligaments structures; each end of a ligament is tangentially linked to a node, as shown in Figure 1a. The number of ligaments linked to one node identifies the chiral lattice structures type as trichiral, tetrachiral or hexachiral structures for 3, 4 or 6 tangential ligaments connected to one node, respectively. The anti prefix for chiral auxetic structures is meant to define the spatial relationships among chiral network nodes and ligaments. Chiral lattice auxetic structures with cylindrical nodes facing the direction opposite the ligament tips are called chiral network systems; when cylinders run in the same direction as the ligament, they are called antichiral systems. Nevertheless, not all chiral network systems exhibit negative Poisson’s ratios; 4 and 6 ligament linked systems and short ligament-limited anti-trichiral network systems just have auxeticity [31]. The chiral hexagonal auxetic lattice structure was selected for this study, which exhibits full-wave shaped ligament deformation. The chiral hexagonal unit and topology parameters are shown in Figure 1. The structure consists of equal-sized cylinders, or nodes, linked by the ligaments of the same length L. The extrusion length of the chiral unit is indicated by e. The nodes’ outer radii are denoted by r, and the negative Poisson’s ratio is generated by the bending of the ligaments around the nodes. Chiral system deformation begins with node rotation, and ligament bending as a result of node rotation. During the deformation of the chiral unit, two different ligament deformations can be seen according to the type of chiral network system. The full wave-shaped ligament deformations can occur in the chiral systems and half-wave shaped ligament deformations in the anti chiral network systems. The full-wave shaped ligaments absorb more energy in crashworthiness and compression applications [3].
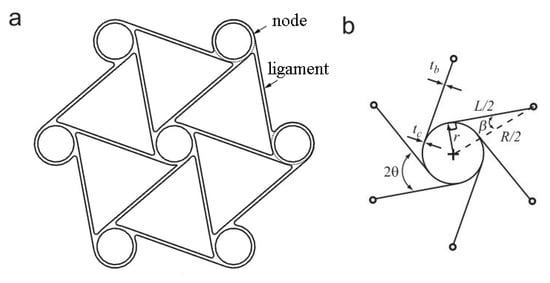
Materials 15 01520 g001 550
Figure 1. Hexagonal chiral element: (a) representative unit and (b) geometrical parameters.

The angle of θ and β are the topology parameters, and their relationships between other parameters are given in Equation 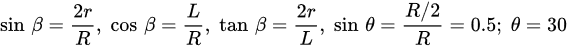(1).

(1)

Equation (1) defines the topology layout and the ligament orientations with regard to the imaginary line through each node’s center [7][17]. Among the parameters, cosβ has a special place by dominating the chiral geometry significantly. According to the study of Spadoni et al. [32], L/R mainly affects the mechanical performance of the chiral structure. In the study of Prall and Lakes, −1 Poisson’s ratio of chiral structure was shown theoretically with a rigid node assumption, and the elastic modulus of a chiral structure is given in Equation (2) [7]. Es is the Young’s modulus of lattice cell constituent material. To obtain stiffer chiral structures, the thickness of the chiral units can be increased, and the ligament length and radius of nodes can be decreased. Two different chiral units with different thicknesses of 0.8 and 1.6 mm, called C1 and C2 hereafter, respectively, were considered in this study to investigate the effect of thickness.

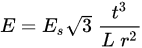(2)

2.2. Materials and Processing

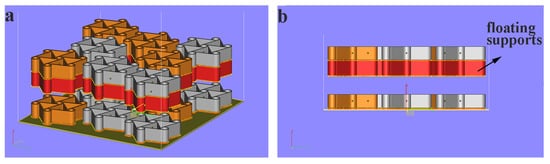
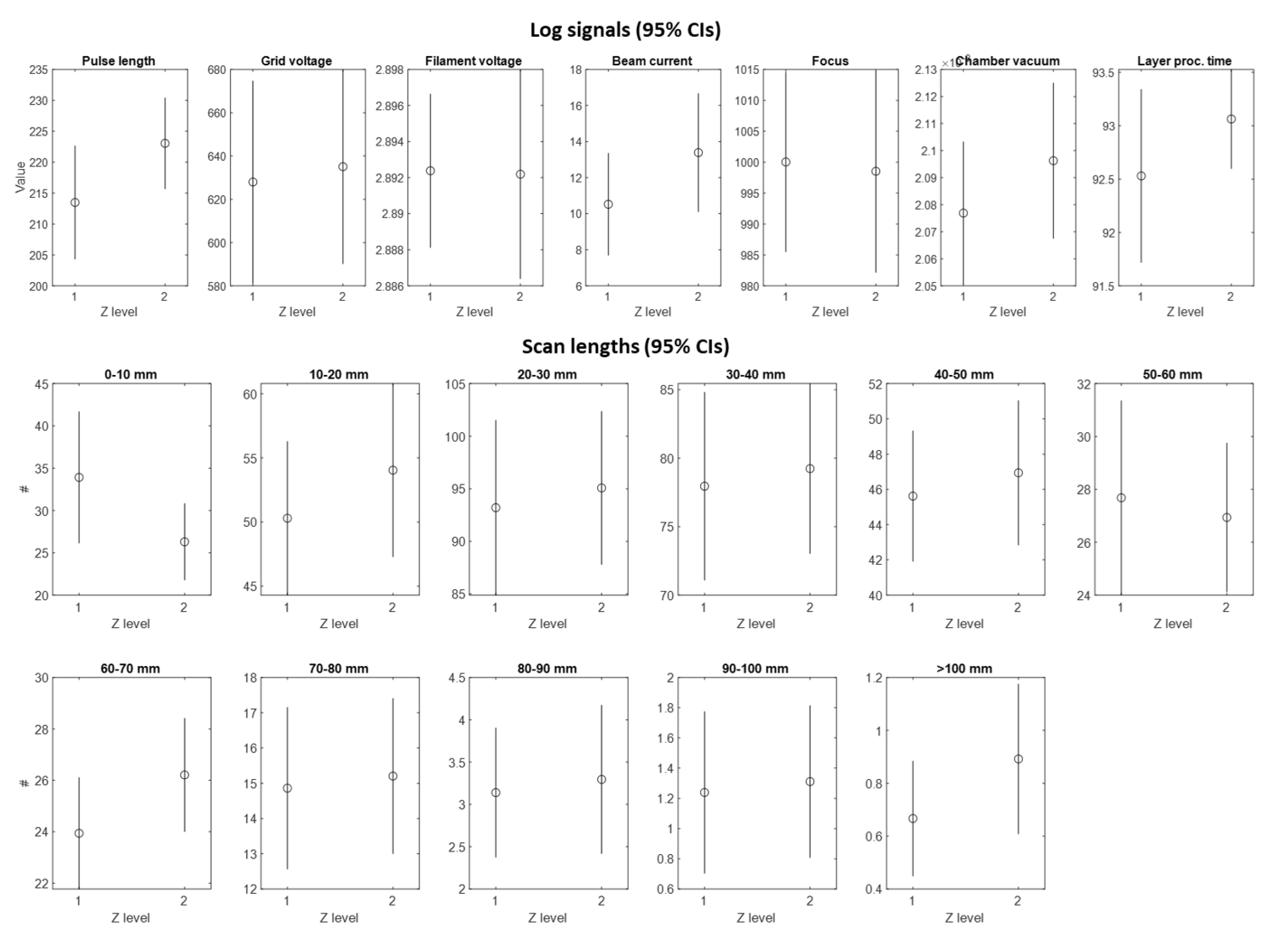
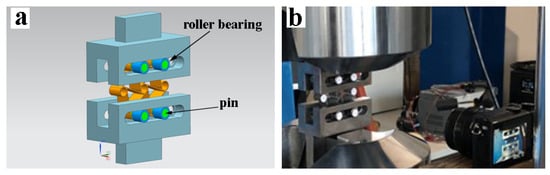
In this study, an ARCAM A2 system was used for the additive production of tensile, bending and chiral unit specimens. Sixteen chiral unit samples were produced in the same build by using gas atomized Ti6Al4V ELI (extra low interstitial) powder with an average size of 45–106 μm. Table 1 shows the powder’s chemical composition. The mechanical specifications indicated by the machine vendor for this material are listed as Young’s modulus, yield stress, ultimate tensile strength and elongation equal to 120 GPa, 930 MPa, 970 MPa and 16%, respectively [33]. The samples were produced on two different levels along the z-axis, as shown in Figure 2. By exploiting the pre-sintered nature of the powder, caused by the high-temperature pre-heating phase, “floating supports” were used for samples in the upper z level, as shown in Figure 2b. Dummy cylinders were included in the build to enhance the homogeneity of the thermal load within the entire build volume, as exhibited in Figure 3a. Four groups of tensile and bending specimens, including five specimens in each group, were produced. Groups can be defined as 0.8 mm thick vertical and horizontal, and 1.6 mm thick vertical and horizontal builds. The samples were produced with a layer thickness of 50 μm while applying default process parameters provided by the machine vendor for this powder.

Materials 15 01520 g002 550
Figure 2. Floating parts production in EBM: (a) iso view and (b) front view.
Materials 15 01520 g003 550
Figure 3. EBM printed parts: (a) printed parts in powder cake, (b) as-built and sandblasted chiral parts and (c) as-built and sandblasted tensile specimens.
Table 1. Chemical specifications of Arcam Ti6Al4V ELI [33].
Aluminium Vanadium Carbon Iron Oxygen Nitrogen Hydrogen Titanium
6.0% 4.0% 0.03% 0.10% 0.10% 0.01% <0.003% Balance
The surface finish is an important factor in the analysis of the mechanical performances of EBM printed parts, as EBM yields rougher surfaces than other AM processes. Polished specimens exhibit better strain at failure values for as-built parts thanks to the mitigation of surface irregularities that may cause crack initiations, and therefore stress concentration and premature failure [34]. Poor surface roughness and the presence of powder particles sintered on the surface may affect the stress calculation because of undesired variability and biases in cross-sectional area estimation. In this study, all samples were sandblasted with a fixed sandblasting cycle duration of 5 s for each surface. Surface roughness measurements were performed before and after the sandblasting operation. Figure 3 shows the samples in the pre-sintered bulk of powder at the end of the EBM process (Figure 3a); the as-built and sandblasted chiral unit components (Figure 3b); and the as-built and sandblasted tensile specimens that were already included in the same build (Figure 3c). In addition, a Hitachi Tabletop Microscope TM3000 was used to measure the effective cross-sectional areas after tensile specimens were cut from the gauge region and polished using a mechanical polisher with 1200 grit sandpaper.
For the characterization analysis presented in this study, the avoidance of nonhomogeneous process conditions in different locations of the build waws of great importance. In particular, before testing the chiral sample performances, the researchers carried out an analysis to verify that process conditions remained stable during the production of samples on the two different levels in z direction. The verification was based on analyzing the so-called “log signals”—i.e., signals measured during the process—and on a layer-by-layer basis by means of sensors embedded in the EBM system. Various authors [35][36] discussed the suitability of these signals for determining the stability of the process and predicting variations in the final quality and performances of the products. These signals enclose information about the vacuum conditions, the regularity of the powder deposition, the energy input to the material, the process parameters adapted by embedded optimization algorithms, etc. A subset of most critical signals was identified, and statistical analysis was performed to compare signals acquired during the production of chiral samples placed at two different z levels.
One first family of log-signals included (i) the pulse length of powder sensors, which indicates the amount of powder spread in each layer; (ii) the grid cup voltage, indicating the voltage used to control the electron emission; (iii) the filament voltage, i.e., the cathode voltage used to generate the beam; (iv) the beam current, indicating the energy input to the material; (v) the beam focus, i.e., the current applied to focus and defocus the beam; (vi) the vacuum level in the chamber; and (vii) the total time needed to process each layer. A shift in one (or more) signal belonging to this family would have indicated a variation in the process conditions that could have had detrimental effects on the homogeneity of the microstructural and mechanical properties of parts built at different levels.
The second family of signals consisted of the number of so-called “scan lengths” in each layer. The EBM controller adapts the beam current and the scan speed along each track as a function of the length of the track. The information about the number of scan lengths in different length ranges is made available by the controller for each layer. A shift in the number of scan lengths is an indication of a local variation of the actual energy density, which may introduce local defects and generate non-uniform microstructural properties.
The two levels in the z plane are denoted as level 1 (bottom) and level 2 (top). Figure 4 shows the 95% confidence intervals (CIs) of the mean values in these two levels for each analyzed signal. The analysis confirmed that none of the considered signals exhibited a statistically significant variation in the mean and standard deviation with a family-wise confidence level of 95%. This allowed us to consider the chiral samples produced at different levels as replicates and to neglect any possible undesired location effect.
/media/item_content/202202/621c2f300ff50materials-15-01520-g004.png
Figure 4. The 95% CIs for the mean log-signals at two different levels along z direction where the chiral samples were produced, where level 1 indicates the bottom level and level 2 indicates the top level.

2.3. Procedures for Mechanical Characterization and Testing

EBM printed parts show anisotropic behavior due to the layerwise production method. Accordingly, the mechanical properties of the EBM printed chiral units can be properly analyzed only if a complete characterization of EBM printed material is carried out. Tensile tests were performed in accordance with ASTM E8M for characterizing EBM printed Ti6Al4V parts and elucidating the mechanical properties. Moreover, three-point bending tests were performed, by adopting a testing jig with a span length of 15 mm, and a pin radius of 1.5 mm was used. The test rate for bending was defined as 1.47 mm/min according to having the same strain rate as the tensile test. The test specimens used in the bending tests were 32×6 mm with 0.8 and 1.6 mm thicknesses. Both tensile and bending test specimens were produced in two different directions, 0∘ and 90∘.

In all tests, MTS 810 Material Test System (MTS Systems Corporation, Eden Prairie, MN, USA) was used with MTS 647 Hydraulic Wedge Grip (MTS Systems Corporation, Eden Prairie, MN, USA), and MTS 634.31F-24 (MTS Systems Corporation, Eden Prairie, MN, USA) extensometer was utilized in the tensile tests. As for the crush tests, two rigid plates were used to compress chiral units and lubricant applied to the surface of rigid plates to enable the free movement of the chiral elements, as seen in Figure 5. In addition, for the chiral lattice cyclic compression tests, an additional specific fixture was designed to accomplish the tests, which consisted of two wide steel forks, with horizontal grooves. Pins were inserted in the four lower and upper nodes of the chiral element, and roller bearings were attached to the pins to allow them to slide in the grooves. The design and illustration of fixture and the test layout are shown in Figure 6a. Therefore, the two upper and lower nodes of chiral elements were allowed to move laterally and to rotate while the unit was compressed, as seen in Figure 6a. The test velocity was defined as 1 mm/min. Transverse strains were measured to calculate Poisson’s ratio. For measurement of transverse deformation, all tests were recorded with a high definition camera as seen in Figure 6b, and speckled papers were placed on the nodes to track their movements in the cyclic tests.
Materials 15 01520 g005 550
Figure 5. Crush test setup and specimens of chiral units with (a) 0.8 mm and (b) 1.6 mm ligament thickness.
Materials 15 01520 g006 550
Figure 6. Test setup for cyclic loading showing (a) the design and illustration of text fixture and test layout (b) produced text fixture and experimental layout.
The chiral elements produced with different thicknesses of 0.8 and 1.6 mm were tested with a compressive load profile to investigate their elastic limits by applying large displacements without experiencing permanent deformations, degradation or failures. The compressive load profile is depicted in Figure 7. The test first started with compression to a limit of 0.5 mm displacement, and thereafter a displacement controlled tensile phase was commenced and continued in which the load reached zero, and then compression started again and proceeded until the defined displacement limit.
Materials 15 01520 g007 550
Figure 7. Compressive load profile for chiral lattices.

References

  1. Evans, K.E.; Nkansah, M.; Hutchinson, I.; Rogers, S. Molecular network design. Nature 1991, 353, 124.
  2. Lakes, R. Foam structures with a negative Poisson’s ratio. Science 1987, 235, 1038–1041.
  3. Alderson, A.; Alderson, K.L.; Attard, D.; Evans, K.E.; Gatt, R.; Grima, J.N.; Miller, W.; Ravirala, N.; Smith, C.; Zied, K. Elastic constants of 3-, 4- and 6-connected chiral and anti-chiral honeycombs subject to uniaxial in-plane loading. Compos. Sci. Technol. 2010, 70, 1042–1048.
  4. Dirrenberger, J.; Forest, S.; Jeulin, D. Effective elastic properties of auxetic microstructures: Anisotropy and structural applications. Int. J. Mech. Mater. Des. 2013, 9, 21–33.
  5. Grima, J.N.; Chetcuti, E.; Manicaro, E.; Attard, D.; Camilleri, M.; Gatt, R.; Evans, K.E. On the auxetic properties of generic rotating rigid triangles. Proc. R. Soc. A Math. Phys. Eng. Sci. 2011, 468, 810–830.
  6. Chen, Y.; Scarpa, F.; Liu, Y.; Leng, J. Elasticity of anti-tetrachiral anisotropic lattices. Int. J. Solids Struct. 2013, 50, 996–1004.
  7. Prall, D.; Lakes, R. Properties of a chiral honeycomb with a Poisson’s ratio of—1. Int. J. Mech. Sci. 1997, 39, 305–314.
  8. Wu, W.; Hu, W.; Qian, G.; Liao, H.; Xu, X.; Berto, F. Mechanical design and multifunctional applications of chiral mechanical metamaterials: A review. Mater. Des. 2019, 180, 107950.
  9. Mizzi, L.; Attard, D.; Gatt, R.; Pozniak, A.A.; Wojciechowski, K.W.; Grima, J.N. Influence of translational disorder on the mechanical properties of hexachiral honeycomb systems. Compos. Part B Eng. 2015, 80, 84–91.
  10. Li, H.; Ma, Y.; Wen, W.; Wu, W.; Lei, H.; Fang, D. In plane mechanical properties of tetrachiral and antitetrachiral hybrid metastructures. J. Appl. Mech. 2017, 84, 081006.
  11. Günaydın, K.; Eren, Z.; Kazancı, Z.; Scarpa, F.; Grande, A.M.; Türkmen, H.S. In-plane compression behavior of anti-tetrachiral and re-entrant lattices. Smart Mater. Struct. 2019, 28, 115028.
  12. Gunaydin, K.; Tamer, A.; Turkmen, H.S.; Sala, G.; Grande, A.M. Chiral-Lattice-Filled Composite Tubes under Uniaxial and Lateral Quasi-Static Load: Experimental Studies. Appl. Sci. 2021, 11, 3735.
  13. Yu, H.; Wu, W.; Zhang, J.; Chen, J.; Liao, H.; Fang, D. Drastic tailorable thermal expansion chiral planar and cylindrical shell structures explored with finite element simulation. Compos. Struct. 2019, 210, 327–338.
  14. Liu, Y.; Hu, H. A review on auxetic structures and polymeric materials. Sci. Res. Essays 2010, 5, 1052–1063.
  15. Mir, M.; Ali, M.N.; Sami, J.; Ansari, U. Review of mechanics and applications of auxetic structures. Adv. Mater. Sci. Eng. 2014, 2014, 753496.
  16. Yang, W.; Li, Z.M.; Shi, W.; Xie, B.H.; Yang, M.B. Review on auxetic materials. J. Mater. Sci. 2004, 39, 3269–3279.
  17. Spadoni, A.; Ruzzene, M.; Scarpa, F. Global and local linear buckling behavior of a chiral cellular structure. Phys. Status Solidi (b) 2005, 242, 695–709.
  18. Lorato, A.; Innocenti, P.; Scarpa, F.; Alderson, A.; Alderson, K.; Zied, K.; Ravirala, N.; Miller, W.; Smith, C.; Evans, K. The transverse elastic properties of chiral honeycombs. Compos. Sci. Technol. 2010, 70, 1057–1063.
  19. Lu, Q.; Qi, D.; Li, Y.; Xiao, D.; Wu, W. Impact energy absorption performances of ordinary and hierarchical chiral structures. Thin-Walled Struct. 2019, 140, 495–505.
  20. Spadoni, A.; Ruzzene, M.; Scarpa, F. Dynamic response of chiral truss-core assemblies. J. Intell. Mater. Syst. Struct. 2006, 17, 941–952.
  21. Tee, K.; Spadoni, A.; Scarpa, F.; Ruzzene, M. Wave propagation in auxetic tetrachiral honeycombs. J. Vib. Acoust. 2010, 132, 031007.
  22. Spadoni, A.; Ruzzene, M.; Gonella, S.; Scarpa, F. Phononic properties of hexagonal chiral lattices. Wave Motion 2009, 46, 435–450.
  23. Liu, X.; Hu, G.; Sun, C.; Huang, G. Wave propagation characterization and design of two-dimensional elastic chiral metacomposite. J. Sound Vib. 2011, 330, 2536–2553.
  24. Zhang, K.; Zhao, P.; Hong, F.; Yu, Y.; Deng, Z. On the directional wave propagation in the tetrachiral and hexachiral lattices with local resonators. Smart Mater. Struct. 2019, 29, 015017.
  25. Zhu, Y.; Wang, Z.P.; Poh, L.H. Auxetic hexachiral structures with wavy ligaments for large elasto-plastic deformation. Smart Mater. Struct. 2018, 27, 055001.
  26. Tancogne-Dejean, T.; Karathanasopoulos, N.; Mohr, D. Stiffness and strength of hexachiral honeycomb-like metamaterials. J. Appl. Mech. 2019, 86.
  27. Dirrenberger, J.; Forest, S.; Jeulin, D. Elastoplasticity of auxetic materials. Comput. Mater. Sci. 2012, 64, 57–61.
  28. Bacigalupo, A.; Gambarotta, L. Homogenization of periodic hexa-and tetrachiral cellular solids. Compos. Struct. 2014, 116, 461–476.
  29. Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure Furthermore, Properties; Cambridge University Press: Cambridge, MA, USA, 1999.
  30. Heinl, P.; Rottmair, A.; Körner, C.; Singer, R.F. Cellular titanium by selective electron beam melting. Adv. Eng. Mater. 2007, 9, 360–364.
  31. Bacigalupo, A.; De Bellis, M.L. Auxetic anti-tetrachiral materials: Equivalent elastic properties and frequency band-gaps. Compos. Struct. 2015, 131, 530–544.
  32. Spadoni, A.; Ruzzene, M. Numerical and experimental analysis of the static compliance of chiral truss-core airfoils. J. Mech. Mater. Struct. 2007, 2, 965–981.
  33. Ti6Al4V ELI Titanium Alloy Arcam EBM System; Technical Report; Arcam: Mölndal, Sweden, 2019.
  34. De Formanoir, C.; Michotte, S.; Rigo, O.; Germain, L.; Godet, S. Electron beam melted Ti–6Al–4V: Microstructure, texture and mechanical behavior of the as-built and heat-treated material. Mater. Sci. Eng. A 2016, 652, 105–119.
  35. Steed, C.A.; Halsey, W.; Dehoff, R.; Yoder, S.L.; Paquit, V.; Powers, S. Falcon: Visual analysis of large, irregularly sampled, and multivariate time series data in additive manufacturing. Comput. Graph. 2017, 63, 50–64.
  36. Chandrasekar, S.; Coble, J.B.; Yoder, S.; Nandwana, P.; Dehoff, R.R.; Paquit, V.C.; Babu, S.S. Investigating the effect of metal powder recycling in Electron beam Powder Bed Fusion using process log data. Addit. Manuf. 2020, 32, 100994.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Engineering, Aerospace; Engineering, Manufacturing
Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register : Kadir Gunaydin
View Times: 631
Revisions: 2 times (View History)
Update Date: 28 Feb 2022
Table of Contents
    1000/1000
    Hot Most Recent
    Notice
    You are not a member of the advisory board for this topic. If you want to update advisory board member profile, please contact office@encyclopedia.pub.
    OK
    Confirm
    Only members of the Encyclopedia advisory board for this topic are allowed to note entries. Would you like to become an advisory board member of the Encyclopedia?
    Yes
    No
    Academic Video Service
    Feedback