Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Jiahuan Lin
 + 1601 word(s) 1601 2022-01-20 05:05:16 |
2 format is correct
Yvaine Wei
 + 3 word(s) 1604 2022-02-08 03:02:47 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Lin, J. Blade for Offshore Floating Wind Turbine Model. Encyclopedia. Available online: https://encyclopedia.pub/entry/19156 (accessed on 19 April 2024).
Lin J. Blade for Offshore Floating Wind Turbine Model. Encyclopedia. Available at: https://encyclopedia.pub/entry/19156. Accessed April 19, 2024.
Lin, Jiahuan. "Blade for Offshore Floating Wind Turbine Model" Encyclopedia, https://encyclopedia.pub/entry/19156 (accessed April 19, 2024).
Lin, J. (2022, February 07). Blade for Offshore Floating Wind Turbine Model. In Encyclopedia. https://encyclopedia.pub/entry/19156
Lin, Jiahuan. "Blade for Offshore Floating Wind Turbine Model." Encyclopedia. Web. 07 February, 2022.
Blade for Offshore Floating Wind Turbine Model
Edit
This entry is adapted from the peer-reviewed paper 10.3390/jmse10020132

The Froude-scaled offshore floating wind turbine model is inevitably affected by the Reynolds number effect, making the model unable to correctly reproduce the thrust performance of the reference wind turbine (RWT). To solve this problem, an Xfoil-AirfoilPrep-Matlab (XAM) system and a wide tip speed ratio search method (WTSM) are proposed to design a wide tip speed ratio (TSR) thrust-match model blade. The XAM system is utilized to select the best airfoil for WTSM by calculating the lift and drag coefficients of several airfoils. The WTSM is utilized to optimize the blade chord and twist. It formalizes the blade chord and twist by polynomials and then optimizes the polynomial coefficients. The thrust coefficients construct the optimization object at different TSRs. For validating the effect of the redesigned blade, the thrust performance is compared to that of the RWT blade. In addition, the thrust performance of redesigned blade at different pitch angles is also calculated and compared to those of the RWT blade. Results show that the thrust performance of redesigned blade matches well with that of the RWT blade at 0 pitch angle, and it can also match the variations of that of the RWT blade at the other pitch angles well.

offshore floating wind turbine redesigned blade Reynolds number effect

1. Introduction

With the development of the offshore floating wind turbine (OFWT) technique, the capacity and geometry of OFWTs are rapidly increasing [1][2][3][4][5]. The increases promote the need for the OFWT design cost reduction approach [6]. In this scenario, the scaled model method is the most commonly used one [7][8]. It works by constructing a model to validate the static and dynamic characteristics of OFWT. However, due to the Reynolds number effect (RNE), the Froude-scaled OFWT model cannot correctly reproduce the aerodynamic performance of the reference wind turbine (RWT) [9][10][11][12], especially the thrust performance.
To solve this problem, the redesigning blade method is proposed and widely studied [13]. It reproduces the thrust performance of the RWT blade by designing a dedicated blade. The design includes two steps. The first step is choosing a thin airfoil to replace the original airfoils used in the RWT blade. The second step is adjusting the blade geometry, which is mainly described by the blade chord and twist, by manual or optimization algorithm to obtain a redesigned blade matching the RWT blade in thrust performance.

2. Scaling Laws and RNE

To design a wide tip speed ratio (TSR) thrust matched blade, the reason for RNE and its effect mechanism should be deeply studied. Thus, the scaling laws of the Froude-scaled OFWT model are first introduced. Then, the inevitability of RNE is analyzed based on the scaling laws, and the effect mechanism of RNE is constructed. Finally, based on the effect mechanism of RNE, a preliminary airfoil selection method is proposed to guidance redesigning the blade.

2.1. Scaling Laws

The OFWT model is commonly designed to satisfy the geometry, kinematics and dynamics similarity [14]. To reach these goals, the scaling factors of different properties should be fully considered. 

2.2. RNE

To accurately study the influence of RNE on the performance of airfoils, the DU40 airfoil is taken as the example to compare the lift and drag coefficients (CL and CD) of airfoils at the reference and model Reynolds numbers. The results are shown in Figure 1, and α is the angle of attack. It shows that there are several significant changes in airfoil performance resulting from RNE. The CL significantly decreases, and the CD slightly increases. It means the peak CL/CD also decreases significantly. As the Blade Element Momentum (BEM) points that, the CT of blade sections is mainly influenced by the peak CL of airfoil, the valley CD and the peak CL/CD of airfoil [15][16]. Thus, to design a thrust match blade, airfoils with larger peak CL, smaller valley CD and larger CL/CD are needed first.
Jmse 10 00132 g001 550
Figure 1. The aerodynamic performance of DU40 airfoil at the reference and model Reynolds numbers. (a) The lift coefficient. (b) The drag coefficient.

3. Airfoil Selection

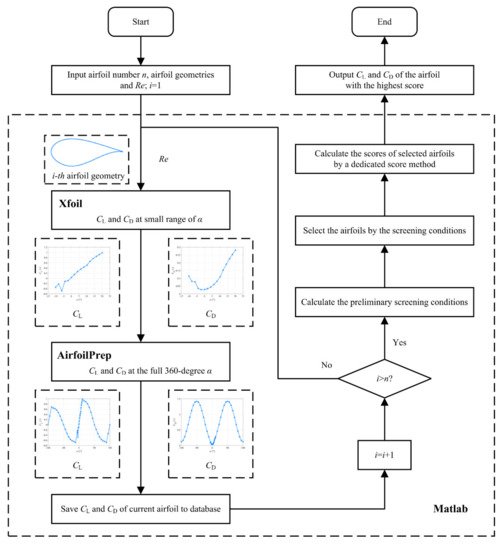
3.1. Xfoil-AirfoilPrep-Matlab (XAM) System

To find the required airfoils, the CL and CD of several airfoils should be calculated and compared with each other. Based on this goal, a XAM system, which integrates Xfoil [17], AirfoilPrep [18] and Matlab software, is proposed. This system can fulfill the calculation of the CL and CD of several airfoils at the full 360-degree angle of attack, the extraction of the critical data and the comparison of the aerodynamic performance of airfoils.
The flowchart of the XAM system is shown in Figure 2. Firstly, the studied airfoil number, airfoil geometries and Re are read. Secondly, a bat file is written based on airfoil geometries and used to drive the Xfoil. Thirdly, the CL and CD at a small range of α are processed to the full 360-degree CL and CD data by AirfoilPrep. Fourthly, the preliminary screening conditions are determined according to the maximum peak CL, the minimum valley CD and the maximum peak CL/CD of airfoils. Then, several airfoils are selected based on the preliminary screening conditions. Afterward, the scores of the selected airfoils are calculated by a dedicated score method. Finally, the CL and CD of the airfoil with the highest score are output.
Jmse 10 00132 g002 550
Figure 2. The flow-chart of XAM system.

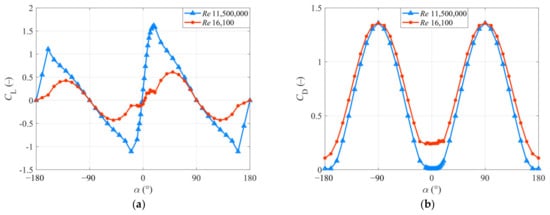
3.2. Result and Discussion of Airfoil Performance

The geometry and aerodynamic performance of AG 14 airfoil at the model Reynolds number are shown in Figure 3 and Figure 4, respectively. 
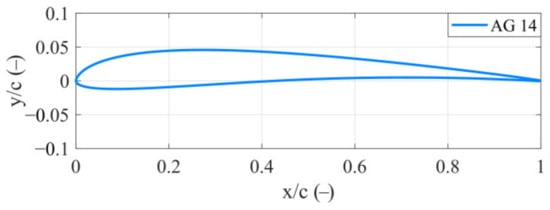
Jmse 10 00132 g003 550
Figure 3. The geometry of AG 14 airfoil.
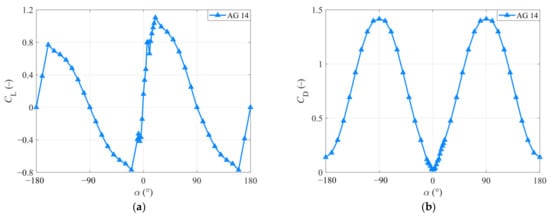
Jmse 10 00132 g004 550
Figure 4. The aerodynamic performance of AG 14 airfoil at the model Reynolds number. (a) The lift coefficient. (b) The drag coefficient.

4. Redesigning Blade Solution

4.1. Wide Tip Speed Ratio Search Method (WTSM)

The rated thrust coefficient is usually taken as the optimization object of redesigning the blade in the previous studies. However, it cannot promise the thrust performance of the OFWT model matching the RWT blade under other working conditions. This will lead to deviations in research related to unsteady inflow wind, wake and control strategy. To solve this problem, a WTSM is proposed to design a wide TSR thrust-match blade. The WTSM reaches this goal by taking the thrust coefficients at multi-TSR as the optimization object in the design process. The flowchart of WTSM is shown in Figure 5. First is fitting the blade chord and twist of the RWT blade to a quaternary polynomial and a quadratic polynomial, respectively. Second is clarifying the constraints of blade chord and twist. Then, selecting an appropriate alternative airfoil through the XAM system (AG 14 airfoil). Afterward, the blade chord and twist polynomial coefficients are taken as the design variables to search for the result with a minimum target value. Finally, the blade chord and twist are output.
Jmse 10 00132 g005 550
Figure 5. The flow-chart of WTSM.

4.2. Results

In this entry, the population of grasshopper optimization algorithm (GOA) is set as 4000, and the iteration is set as 10. The blade chord and twist results are compared with the RWT blade in Figure 6. It shows that the redesigned blade has an increase in chord and a decrease in twist. The increased blade chord can catch more wind power and slightly increase the Reynolds number. The decreased twist will lead the airfoil, which has poor performance due to the RNE, to operate at a better angle of attack. Similar findings can be found in other studies [19][20]. In addition, the smoothness of the chord and twist curve also prove the advantage of using the polynomial coefficients as the design variable.
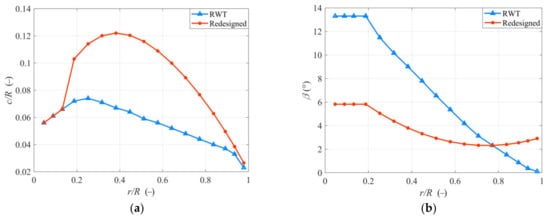
Jmse 10 00132 g006 550
Figure 6. Comparison of the redesigned blade and the RWT blade. (a) Chord. (b) Twist.
The comparison of the thrust coefficient between the redesigned blade and the RWT blade is shown in Figure 7a. The relative error is shown in Figure 7b. To show the effectiveness of WTSM, a blade redesigned by Pattern Search (PS) in 1/50th with Du et al.’s study is also present in Figure 7a and denoted as PS [21].
Jmse 10 00132 g007 550
Figure 7. (a) The thrust coefficient comparison of redesigned blade, RWT blade and PS blade. (b) The relative error of redesigned blade to RWT blade.

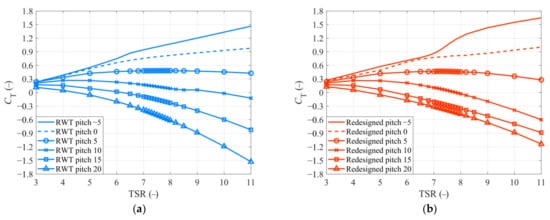
4.3. Aerodynamic Analysis with Different Pitch Angle

To further study the capacity of the redesigned blade in researches related to control strategy, some CT-TSR curves of the redesigned blade and RWT blade with different pitch angles are obtained from OpenFAST and presented in Figure 8. It shows that the CT of the RWT blade decrease with the increase of pitch angle, and this decrease is more obvious with the increase of TSR. Similar trends can also be found on the CT-TSR curves of the redesigned blade. In this scenario, though some deviations can be found between the redesigned blade and the RWT blade except the 0 pitch angle, it still has a great potential in serving for research related to control strategy.
Jmse 10 00132 g008 550
Figure 8. The CT-TSR curves with different pitch angles. (a) RWT blade. (b) Redesigned blade.

5. Conclusions

This entry proposes a XAM system to select the best airfoil for redesigning the blade first. Then a WTSM based on GOA is put forward to optimize the blade chord and twist of the redesigned blade. The main findings are summarized as follows:
  1. A XAM system is constructed to guide the airfoil selection. Based on the XAM system, 767 airfoils are compared with each other according to the preliminary screening conditions and the dedicated score method. Finally, the AG 14 airfoil is selected out as the best airfoil.
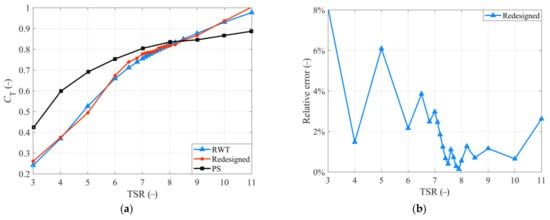
  2. A WTSM is proposed for a wide TSR thrust-match blade. Based on the WTSM, the blade chord and twist of the redesigned blade with AG 14 airfoil is optimized for a better thrust performance. The CT-TSR curve of the redesigned blade is compared with the RWT blade. Moreover, most of the relative errors are less than 5%, except for the working conditions that TSR = 3 (8%) and TSR = 5 (6%). It proves the thrust performance of the redesigned blade matches that of the RWT blade well at a 0 pitch angle.
  3. The thrust coefficients of the proposed redesigned blade in other pitch angles are calculated and compared to those of the RWT blade. Results show that the variations are consistent with the RWT blade. It means that the redesigned blade has great potential in the studies related to control strategy.

References

  1. Global Wind Energy Council. GWEC Global Wind Report; Global Wind Energy Council (GWEC): Brussels, Belgium, 2021.
  2. Ju, S.; Huang, Y.; Huang, Y. Study of optimal large-scale offshore wind turbines. Renew. Energy 2020, 154, 161–174.
  3. Finnegan, W.; Jiang, Y.; Dumergue, N.; Davies, P.; Goggins, J. Investigation and Validation of Numerical Models for Composite Wind Turbine Blades. J. Mar. Sci. Eng. 2021, 9, 525.
  4. Medina, C.; Álamo, G.M.; Quevedo-Reina, R. Evolution of the Seismic Response of Monopile-Supported Offshore Wind Turbines of Increasing Size from 5 to 15 MW including Dynamic Soil-Structure Interaction. J. Mar. Sci. Eng. 2021, 9, 1285.
  5. Chatterjee, J.; Dethlefs, N. Deep learning with knowledge transfer for explainable anomaly prediction in wind turbines. Wind Energy 2020, 23, 1693–1710.
  6. Ghigo, A.; Cottura, L.; Caradonna, R.; Bracco, G.; Mattiazzo, G. Platform optimization and cost analysis in a floating offshore wind farm. J. Mar. Sci. Eng. 2020, 8, 835.
  7. Dao, C.; Kazemtabrizi, B.; Crabtree, C. Wind turbine reliability data review and impacts on levelised cost of energy. Wind Energy 2019, 22, 1848–1871.
  8. Crabtree, C.J.; Zappalá, D.; Hogg, S.I. Wind energy: UK experiences and offshore operational challenges. Proc. Inst. Mech. Eng. Part A J. Power Energy 2015, 229, 727–746.
  9. Lalonde, E.; Vischschraper, B.; Bitsuamlak, G.; Dai, K. Evaluation of a neural network-based surrogate aerodynamic wind turbine model. In Proceedings of the International Conference on Advances in Wind and Structures, Seoul, Korea, 8 July 2020.
  10. Martin, H.R. Development of a Scale Model Wind Turbine for Testing of Offshore Floating Wind Turbine Systems; University of Maine: Orono, ME, USA, 2011; pp. 1–181.
  11. Lee, H.; Lee, D.J. Low Reynolds number effects on aerodynamic loads of a small scale wind turbine. Renew. Energy 2020, 154, 1283–1293.
  12. Gueydon, S.; Judge, F.M.; O’shea, M.; Lyden, E.; Le Boulluec, M.; Caverne, J.; Ohana, J.; Kim, S.; Bouscasse, B.; Thiebaut, F.; et al. Round robin laboratory testing of a scaled 10 mw floating horizontal axis wind turbine. J. Mar. Sci. Eng. 2021, 9, 988.
  13. Meng, L.; He, Y.; Zhao, Y.; Peng, T.; Yang, J. Experimental Study on Aerodynamic Characteristics of the Model Wind Rotor System and on Characterization of a Wind Generation System. China Ocean Eng. 2019, 33, 137–147.
  14. Ruzzo, C.; Muggiasca, S.; Malara, G.; Taruffi, F.; Belloli, M.; Collu, M.; Li, L.; Brizzi, G.; Arena, F. Scaling strategies for multi-purpose floating structures physical modeling: State of art and new perspectives. Appl. Ocean Res. 2021, 108, 102487.
  15. Macháček, M.; Pospíšil, S.; Kozmar, H. Scaling of wind turbine aerodynamics: Wind tunnel experiments. MATEC Web Conf. 2020, 313, 00053.
  16. Gajardo, D.; Escauriaza, C.; Ingram, D.M. Capturing the development and interactions of wakes in tidal turbine arrays using a coupled BEM-DES model. Ocean Eng. 2019, 181, 71–88.
  17. Drela, M. XFOIL: An Analysis and Design System for Low Reynolds Number Airfoils. In Proceedings of the Conference on Low Reynolds Number Airfoil Aerodynamics, Notre Darre, IN, USA, 5–7 June 1989; pp. 1–12.
  18. Hansen, C. AirfoilPrep: An Excel Workbook for Generating Airfoil Tables for AeroDyn and WT_Perf. Available online: https://www.nrel.gov/wind/nwtc/airfoil-prep.html (accessed on 3 December 2021).
  19. Martin, H.R.; Kimball, R.W.; Viselli, A.M.; Goupee, A.J. Methodology for wind/wave basin testing of floating offshore wind turbines. J. Offshore Mech. Arct. Eng. 2014, 136, 020905.
  20. Wen, B.; Tian, X.; Dong, X.; Li, Z.; Peng, Z. Design approaches of performance-scaled rotor for wave basin model tests of floating wind turbines. Renew. Energy 2020, 148, 573–584.
  21. Du, W.; Zhao, Y.; He, Y.; Liu, Y. Design, analysis and test of a model turbine blade for a wave basin test of floating wind turbines. Renew. Energy 2016, 97, 414–421.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Engineering, Marine
Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Jiahuan Lin
View Times: 368
Revisions: 2 times (View History)
Update Date: 08 Feb 2022
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback