
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Piera Fischione | + 5037 word(s) | 5037 | 2022-01-28 07:20:06 | | | |
| 2 | Jason Zhu | Meta information modification | 5037 | 2022-02-08 02:26:27 | | | | |
| 3 | Jason Zhu | Meta information modification | 5037 | 2022-02-08 02:27:30 | | |
Video Upload Options
The idea that the groundwater table plays a role in the mobilization of the sediment grains underlies the application of the beach drainage system (BDS) as a tool able to modify the natural dynamics of groundwater table at sandy beaches. The beach drainage is one of the soft engineering methods aimed to counteract the shoreline retreat related to the sediment redistribution along the beach profile.
1. Introduction
-
reduction of sediment supply;
-
changing in the natural forcing (i.e., changing waves climate, sea-level rise, comminution, subsidence, etc.);
-
interference with human constructions.
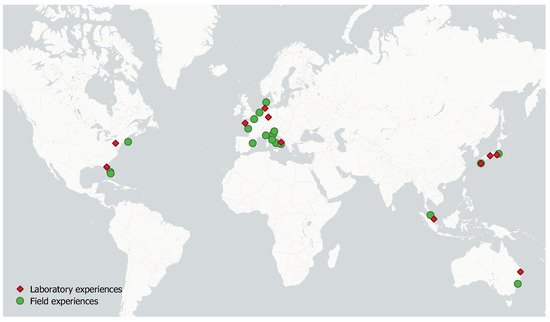
2. Laboratory Experience
3. Field Campaigns
4. Mathematical modeling
The water table is defined as the surface where the pore pressure is atmospheric. Above the free surface, a layer of unsaturated medium is present: the pores between the solid grains are not full of water, but it results to be a three-phase area: liquid (water), solid (grains), and gas (air). The mathematical modeling of the groundwater motion in an unconfined aquifer (i.e., a flow whose upper boundary is represented by a water table) follows the classical approach of the continuum medium for irrotational flow. The simplest approach for the unconfined unsteady flow (since the presence of the time-dependent forcing) is the one-dimensional linearized Boussinesq equation [82], i.e. the combination of Darcy’s law and the mass conservation equation, considering the Dupuit’s assumption [83], which assumes equipotential lines as vertical and streamlines as horizontal and hence a hydrostatic pressure distribution.
References
- Bird, E.C. Coastal Geomorphology: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2011.
- Pasquali, D.; Marucci, A. The Effects of Urban and Economic Development on Coastal Zone Management. Sustainability 2021, 13, 6071.
- Di Risio, M.; Bruschi, A.; Lisi, I.; Pesarino, V.; Pasquali, D. Comparative analysis of coastal flooding vulnerability and hazard assessment at national scale. J. Mar. Sci. Eng. 2017, 5, 51.
- Mangor, K.; Drønen, N.K.; Kærgaard, K.H.; Kristensen, S.E. Shoreline Management Guidelines; DHI Water and Environment: Hørsholm, Denmark, 2017.
- Pasquali, D.; Di Risio, M.; De Girolamo, P. A simplified real time method to forecast semi-enclosed basins storm surge. Estuar. Coast. Shelf Sci. 2015, 165, 61–69.
- Pasquali, D.; Bruno, M.; Celli, D.; Damiani, L.; Di Risio, M. A simplified hindcast method for the estimation of extreme storm surge events in semi-enclosed basins. Appl. Ocean Res. 2019, 85, 45–52.
- Dean, R.G.; Dalrymple, R.A. Coastal Processes with Engineering Applications; Cambridge University Press: Cambridge, UK, 2001.
- Hegde, A.V. Coastal erosion and mitigation methods–Global state of art. Indian J. Geo-Mar. Sci. 2010, 39, 521–530.
- Rey-Valette, H.; Robert, S.; Rulleau, B. Resistance to relocation in flood-vulnerable coastal areas: A proposed composite index. Clim. Policy 2019, 19, 206–218.
- Castellino, M.; Lara, J.L.; Romano, A.; Losada, I.J.; De Girolamo, P. Wave loading for recurved parapet walls in non-breaking wave conditions: Analysis of the induced impulsive forces. Coast. Eng. Proc. 2018, 1, 34.
- Castellino, M.; Romano, A.; Lara, J.L.; Losada, I.J.; De Girolamo, P. Confined-crest impact: Forces dimensional analysis and extension of the Goda’s formulae to recurved parapets. Coast. Eng. 2021, 163, 103814.
- Saponieri, A.; Di Risio, M.; Pasquali, D.; Valentini, N.; Aristodemo, F.; Tripepi, G.; Celli, D.; Streicher, M.; Damiani, L. Beach profile evolution in front of storm seawalls: A physical and numerical study. Coast. Eng. Proc. 2018, 36, 70.
- Celli, D.; Pasquali, D.; De Girolamo, P.; Di Risio, M. Effects of submerged berms on the stability of conventional rubble mound breakwaters. Coast. Eng. 2018, 136, 16–25.
- Celli, D.; Li, Y.; Ong, M.C.; Di Risio, M. The role of submerged berms on the momentary liquefaction around conventional rubble mound breakwaters. Appl. Ocean Res. 2019, 85, 1–11.
- Celli, D.; Li, Y.; Ong, M.C.; Di Risio, M. Random wave-induced momentary liquefaction around rubble mound breakwaters with submerged berms. J. Mar. Sci. Eng. 2020, 8, 338.
- Celli, D.; Pasquali, D.; Fischione, P.; Di Nucci, C.; Di Risio, M. Wave-induced dynamic pressure under rubble mound breakwaters with submerged berm: An experimental and numerical study. Coast. Eng. 2021, 170, 104014.
- Coastal Engineering Research Center (US). Shore Protection Manual; US Army Coastal Engineering Research Center: Washington, DC, USA, 1984; Volume 1.
- Saponieri, A.; Valentini, N.; Di Risio, M.; Pasquali, D.; Damiani, L. Laboratory Investigation on the Evolution of a Sandy Beach Nourishment Protected by a Mixed Soft–Hard System. Water 2018, 10, 1171.
- Bridges, T.S.; Burks-Copes, K.A.; Bates, M.E.; Collier, Z.A.; Fischenich, J.C.; Piercy, C.D.; Russo, E.J.; Shafer, D.J.; Suedel, B.C.; Gailani, J.Z.; et al. Use of Natural and Nature-Based Features (NNBF) for Coastal Resilience; US Army Engineer Research and Development Center, Environmental Laboratory: Vicksburg, MS, USA, 2015.
- Hagedoorn, L.C.; Addo, K.A.; Koetse, M.J.; Kinney, K.; van Beukering, P.J. Angry waves that eat the coast: An economic analysis of nature-based and engineering solutions to coastal erosion. Ocean Coast. Manag. 2021, 214, 105945.
- Van der Nat, A.; Vellinga, P.; Leemans, R.; Van Slobbe, E. Ranking coastal flood protection designs from engineered to nature-based. Ecol. Eng. 2016, 87, 80–90.
- Janssen, S.; Vreugdenhil, H.; Hermans, L.; Slinger, J. On the nature based flood defence dilemma and its Resolution: A game theory based analysis. Sci. Total Environ. 2020, 705, 135359.
- Seddon, N.; Chausson, A.; Berry, P.; Girardin, C.A.; Smith, A.; Turner, B. Understanding the value and limits of nature-based solutions to climate change and other global challenges. Philos. Trans. R. Soc. B 2020, 375, 20190120.
- Pontee, N.; Narayan, S.; Beck, M.W.; Hosking, A.H. Nature-based solutions: Lessons from around the world. In Proceedings of the Institution of Civil Engineers-Maritime Engineering; Thomas Telford Ltd.: London, UK, 2016; Volume 169, pp. 29–36.
- Komar, P.D. Handbook of Coastal Processes and Erosion; CRC Press: Boca Raton, FL, USA, 2018.
- Di Risio, M.; Lisi, I.; Beltrami, G.; De Girolamo, P. Physical modeling of the cross-shore short-term evolution of protected and unprotected beach nourishments. Ocean Eng. 2010, 37, 777–789.
- Turner, I.L.; Leatherman, S.P. Beach dewatering as a’soft’engineering solution to coastal erosion: A history and critical review. J. Coast. Res. 1997, 13, 1050–1063.
- Vesterby, H.D. Method of Causing Sedimentation of Sedimentary Solid Material Transported in a Body of Water, Such as a Lake, a Sea, or an Ocean. U.S. Patent 4,645,377, 24 February 1987.
- Jakobsen, P.D. Method for Coastal Protection. U.S. Patent 6,547,486, 15 April 2003.
- Bruun, P. The coastal drain: What can it do or not do? J. Coast. Res. 1989, 5, 123–125.
- Vesterby, H. Beach face dewatering-the European experience. Alternative technologies in beach preservation. In Proceedings of the 1994 National Conference on Beach Preservation Technology, Tampa, FL, USA, February 1994; pp. 53–68.
- Katoh, K.; Yanagishima, S.i. Field experiment on the effect of gravity drainage system on beach stabilization. In Coastal Engineering 1996; American Society of Civil Engineers: New York, NY, USA, 1997; pp. 2654–2665.
- Mariani, A.; Turner, I. Artificial reefs and beach dewatering as innovative solutions to beach erosion: Lessons learnt from two decades of field experience. In Proceedings of the Coasts and Ports 2013: 21st Australasian Coastal and Ocean Engineering Conference and the 14th Australasian Port and Harbour Conference, Sydney, Australia, 11–13 September 2013; Engineers Australia: Adelaide, Australia, 2013; p. 501.
- Mariani, A.; Carley, J.; Lord, D.; Turner, I.; Cox, R. International Review of Emerging Technologies to Manage Beach Erosion: Do They Really Work? In Proceedings of the Coastal Conference, Vancouver, Canada, 6–9 October 2013; Available online: https://www.coastalconference.com/2013/papers2013/Alessio%20Mariani.pdf (accessed on 20 October 2021).
- Ciavola, P.; Vicinanza, D.; Fontana, E. Beach drainage as a form of shoreline stabilization: Case studies in Italy. In Coastal Engineering 2008; World Scientific: Singapore, 2009; Volume 5, pp. 2646–2658.
- Contestabile, P.; Aristodemo, F.; Vicinanza, D.; Ciavola, P. Laboratory study on a beach drainage system. Coast. Eng. 2012, 66, 50–64.
- Pilkey, O.H.; Cooper, J.A.G. “Alternative” shoreline erosion control devices: A review. In Pitfalls of Shoreline Stabilization; Springer: Dordrecht, The Netherlands, 2012; pp. 187–214.
- Machemehl, J.L. New method for beach erosion control. In Proceedings of the Engineering in the Oceans, American Society of Civil Engineers Specialty Conference, Newark, DE, USA, 9–12 June 1975.
- Kawata, Y.; Tsuchiya, Y. Applicability of sub-sand system to beach erosion control. In Coastal Engineering 1986; American Society of Civil Engineers: New York, NY, USA, 1987; pp. 1255–1267.
- Ogden, M.R. An Experimental Investigation of the Effects of Subsurface Drains on Beach Stabilization. Master’s Thesis, Lehigh University, Bethlehem, PA, USA, 1991.
- Seidel, G.S. An Experimental Investigation of the Effects of Tides on Subsurface Drains Used for Beach Stabilization. Master’s Thesis, Lehigh University, Bethlehem, PA, USA, 1991.
- Sato, M.; Hata, S.; Fukushima, M. An experimental study on beach transformation due to waves under the operation of coastal drain system. In Coastal Engineering 1994; American Society of Civil Engineers: New York, NY, USA, 1995; pp. 2571–2582.
- Oh, T.M.; Dean, R.G. Beach Face Dynamics as Affected by Ground Water Table Elevations. 1992. Available online: https://aquadocs.org/handle/1834/18419 (accessed on 20 October 2021).
- Oh, T.M.; Dean, R.G. Effects of controlled water table on beach profile dynamics. In Coastal Engineering 1994; American Society of Civil Engineers: New York, NY, USA, 1995; pp. 2449–2460.
- Sato, M.; Fukushima, T.; Nishi, R.; Fukunaga, M. On the change of velocity field in nearshore zone due to coastal drain and the consequent beach transformation. In Coastal Engineering 1996; American Society of Civil Engineers: New York, NY, USA, 1997; pp. 2666–2676.
- Weisman, R.N.; Seidel, G.S.; Ogden, M.R. Effect of water-table manipulation on beach profiles. J. Waterw. Port Coast. Ocean. Eng. 1995, 121, 134–142.
- Kanazawa, H.; Matsukawa, F.; Katoh, K.; Hasegawa, I. Experimental study on the effect of gravity drainage system on beach stabilization. In Coastal Engineering 1996; American Society of Civil Engineers: New York, NY, USA, 1997; pp. 2640–2653.
- Lemckert, C. Influence of Beach Dewatering on Edge Waves—A Laboratory Study. J. Coast. Res. 2001, 34, 138–142.
- Law, A.W.K.; Lim, S.Y.; Liu, B.L. A note on transient beach evolution with artificial seepage in the swash zone. J. Coast. Res. 2002, 18, 379–387.
- Gampathi, G.; Chan, S. Influence of groundwater table on beach profile dynamics. J. Inst. Eng. 2005.
- Veltri, P.; Aristodemo, F.; Ciavola, P.; Corvaro, S.; Saponieri, A.; Verbeni, B. Hydrodynamics study of a drained beach. In Coastlab 2010; Universitat Politécnica de Catalunya: Barcelona, Spain, 2010.
- Damiani, L.; Vicinanza, D.; Aristodemo, F.; Saponieri, A.; Corvaro, S. Experimental investigation on wave set up and nearshore velocity field in presence of a BDS. J. Coast. Res. 2011, 64, 55–59.
- Damiani, L.; Aristodemo, F.; Saponieri, A.; Verbeni, B.; Veltri, P.; Vicinanza, D. Full-scale experiments on a beach drainage system: Hydrodynamic effects inside beach. J. Hydraul. Res. 2011, 49, 44–54.
- Aristodemo, F.; Ciavola, P.; Veltri, P.; Saponieri, A. The influence of a Beach Drainage System on wave reflection and surf beat processes. J. Coast. Res. 2011, 64, 455–459.
- Ciavola, P.; Contestabile, P.; Aristodemo, F.; Vicinanza, D. Beach sediment mixing under drained and undrained conditions. J. Coast. Res. 2013, 65, 1503–1508.
- Hasselmann, K.F.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Eake, K.; Euring, J.; Gicnapp, A.; Hasselmann, D.; Kruseman, P.; et al. Measurements of Wind-Wave Growth and Swell Decay during the Joint North Sea Wave Project (JONSWAP). Ergaenzungsheft zur Deutschen Hydrographischen Zeitschrift, Reihe A. 1973. Available online: https://repository.tudelft.nl/islandora/object/uuid%3Af204e188-13b9-49d8-a6dc-4fb7c20562fc (accessed on 20 October 2021).
- Chappell, J.; Eliot, I.G.; Bradshaw, M.P.; Lonsdale, E. Experimental control of beach face dynamics by watertable pumping. Eng. Geol. 1979, 14, 29–41.
- Curtis, W.R.; Davis, J.E. Field Evaluation/Demonstration of a Multisegmented Dewatering System for Accreting Beach Sand in a High-Wave-Energy Environment; US Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1998.
- Vesterby, H. Coastal drain system: A new approach to coastal restoration. Proc. GEO-Coast 1991, 91, 651–654.
- Ovesen, N.; Schuldt, J. Beach Management System-Documentation; Danish Geotechnical Institute: Lyngby, Denmark, 1992.
- Dean, R. Independent Analysis of Beach Changes in the Vicinity of the Stabeach System at Sailfish Point, Florida; Coastal Stabilization Inc.: Colfax, WA, USA, 1990; 16p.
- Turner, I.L.; Masselink, G. Swash infiltration-exfiltration and sediment transport. J. Geophys. Res. Ocean. 1998, 103, 30813–30824.
- Turner, I.L.; Nielsen, P. Rapid water table fluctuations within the beach face: Implications for swash zone sediment mobility? Coast. Eng. 1997, 32, 45–59.
- Masselink, G.; Hughes, M. Field investigation of sediment transport in the swash zone. Cont. Shelf Res. 1998, 18, 1179–1199.
- Plotkin, O. Beach Restoration on Nantucket. Bachelor’s Thesis, Worcester Polytechnic Institute, Worcester, MA, USA, 2013.
- Curtis, W.R.; Davis, J.E.; Turner, I.L. Evaluation of a beach dewatering system: Nantucket, USA. In Coastal Engineering 1996; American Society of Civil Engineers: New York, NY, USA, 1997; pp. 2677–2690.
- Davis, G.A.; Hanslow, D.J.; Hibbert, K.; Nielsen, P. Gravity drainage: A new method of beach stabilisation through drainage of the watertable. In Coastal Engineering 1992; American Society of Civil Engineers: New York, NY, USA, 1993; pp. 1129–1141.
- Sato, M.; Nishi, R.; Nakamura, K.; Sasaki, T. Short-term field experiments on beach transformation under the operation of a coastal drain system. In Soft Shore Protection; Springer: Berlin, Germany, 2003; pp. 171–182.
- Vesterby, H.; Mangor, K.; Refsgaard, A. Modelling groundwater flow in beach profiles for optimising stabilising measures. In Proceedings of the International Coastal Symposium, Rotorua, New Zealand, 24–28 April 2000; Volume 7.
- Lambert, A.; Rey, V.; Samat, O.; Provansal, M. Watertable monitoring on a beach equipped with a dewatering system: Relationship between watertable elevation and beach morphology, preliminary results. In River, Coastal and Estuarine Morphodynamics, Proceedings of the 4th IAHR Symposium on River, Coastal and Estuarine Morphodynamics, RCEM 2005, Urbana, IL, USA, 4–7 October 2005; CRC Press: Boca Raton, FL, USA, 2005; Volume 1, p. 365.
- Fattal, P.; Walker, P. Le drainage de plage: Une méthode douce de stabilisation d’un littoral meuble–Etude de cas aux Sables d’Olonne (Vendée). Xèmes Journées Nationales Génie Côtier–Génie Civil 2008, 243–252.
- Bowman, D.; Ferri, S.; Pranzini, E. Efficacy of beach dewatering—Alassio, Italy. Coast. Eng. 2007, 54, 791–800.
- Damiani, L.; Ranieri, G.; Rossetti, R. Coastal Protection With BMS: The First Experience In Italy. WIT Trans. Built Environ. 2004.
- Vicinanza, D.; Guida, A.; Ferrante, V.; Ciavola, P. Performance of a beach dewatering system—Chiaiolella beach, Procida Island, Italy. J. Coast. Res. 2010, 26, 753–761.
- Serra, J.; Bautista, R.; Montori, C.; Maia, L.P. Beach dewatering system, results from a pilot plant installation in the Ebro Delta. In Proceedings of the 4th EEGS Meeting, European Association of Geoscientists & Engineers, Barcelona, Spain, 1 July 2010; p. cp-43-00069.
- Jakobsen, P.; Brøgger, C. Coastal protection based on Pressure Equalization Modules (PEM). In Proceedings of the Conference ICS 2007, Gold Coast, Australia, 16–20 April 2007.
- Jakobsen, P.; Brøgger, C. Environmentally Friendly Coastal Protection Based on Vertical Drains. In Coastal Engineering 2008; World Scientific: Singapore, 2009; Volume 5, pp. 4712–4724.
- Brøgger, C.; Jakobsen, P. Beach nourishment combined with sic vertical drain in Malaysia. In Coastal Engineering 2008; World Scientific: Singapore, 2009; Volume 5, pp. 4725–4737.
- Christensen, K.W.; Gable, F.J. Results of a 3-year beach erosion control project in Hillsboro beach, Florida, utilizing pressure equalizing modules (PEM). Coast. Eng. Proc. 2018, 36, 25.
- Walstra, D.; Brière, C.; Vonhögen-Peeters, L. Evaluating the PEM passive beach drainage system in a 4-year field experiment at Egmond (The Netherlands). Coast. Eng. 2014, 93, 1–14.
- Bain, O.; Toulec, R.; Combaud, A.; Villemagne, G.; Barrier, P. Five years of beach drainage survey on a macrotidal beach (Quend-Plage, northern France). Comptes Rendus Geosci. 2016, 348, 411–421.
- Bear, J. Dynamics of Fluids in Porous Media; Courier Corporation: North Chelmsford, MA, USA, 1972.
- Horn, D.P. Measurements and modelling of beach groundwater flow in the swash-zone: A review. Cont. Shelf Res. 2006, 26, 622–652.
- Steggewentz, J.H. De Invloed van de Getijbeweging van Zeeën en Getijrivieren op de Stijghoogte van Grondwater. Doctoral Thesis, 1933. Available online: http://resolver.tudelft.nl/uuid:a16c3f5b-822c-40cc-9a9c-510f60390ad9 (accessed on 20 October 2021).
- Kirkham, D. Seepage of steady rainfall through soil into drains. Eos Trans. Am. Geophys. Union 1958, 39, 892–908.
- Parlange, J.Y.; Stagnitti, F.; Starr, J.; Braddock, R. Free-surface flow in porous media and periodic solution of the shallow-flow approximation. J. Hydrol. 1984, 70, 251–263.
- Nielsen, P. Tidal dynamics of the water table in beaches. Water Resour. Res. 1990, 26, 2127–2134.
- Nielsen, P.; Aseervatham, R.; Fenton, J.D.; Perrochet, P. Groundwater waves in aquifers of intermediate depths. Adv. Water Resour. 1997, 20, 37–43.
- Liu, P.L.F.; Wen, J. Nonlinear diffusive surface waves in porous media. J. Fluid Mech. 1997, 347, 119–139.
- Fischione, P.; Pasquali, D.; Di Nucci, C.; Di Risio, M.; Saponieri, A. Groundwater Levels in a Drained Beach in Long and Short Waves Conditions. Coast. Struct. 2019, 2019, 1034–1043.
- Van de Giesen, N.; Parlange, J.Y.; Steenhuis, T. Transient flow to open drains: Comparison of linearized solutions with and without the Dupuit assumption. Water Resour. Res. 1994, 30, 3033–3039.
- Dominick, T.F.; Wilkins, B., Jr.; Roberts, H. Mathematical model for beach groundwater fluctuations. Water Resour. Res. 1971, 7, 1626–1635.
- Turner, I.L. Simulating the influence of groundwater seepage on sediment transported by the sweep of the swash zone across macro-tidal beaches. Mar. Geol. 1995, 125, 153–174.
- Baird, A.J.; Horn, D.P. Monitoring and modelling groundwater behaviour in sandy beaches. J. Coast. Res. 1996, 12, 630–640.
- Raubenheimer, B.; Guza, R.; Elgar, S. Watertable fluctuations in a sandy ocean beach. In Coastal Engineering 1998; American Society of Civil Engineers: New York, NY, USA, 1999; pp. 3588–3600.
- Li, L.; Barry, D.; Pattiaratchi, C.; Masselink, G. BeachWin: Modelling groundwater effects on swash sediment transport and beach profile changes. Environ. Model. Softw. 2002, 17, 313–320.
- Ang, L.; Sum, C.; Baldock, T.; Li, L.; Nielsen, P. Measurement and modelling of controlled beach groundwater levels under wave action. Measurement 2004, 13, 17.
- Li, L.; Barry, D.; Pattiaratchi, C. Modeling coastal ground-water response to beach dewatering. J. Waterw. Port Coast. Ocean Eng. 1996, 122, 273–280.
- Li, L.; Barry, D.; Pattiaratchi, C. Numerical modelling of tide-induced beach water table fluctuations. Coast. Eng. 1997, 30, 105–123.
- Karambas, T.V.; Ioannidis, D. ‘Soft’shore protection by a beach drainage system. Glob. Nest J. 2013, 15, 295–304.
- Karambas, T.V. Modelling of infiltration-exfiltration effects of cross-shore sediment transport in the swash zone. Coast. Eng. J. 2003, 45, 63–82.
- Saponieri, A.; Damiani, L. Groundwater flow on a drained beach. Comput. Methods Exp. Meas. XVI 2013, 55, 249.
- Saponieri, A.; Damiani, L. Numerical analysis of infiltration in a drained beach. Int. J. Sustain. Dev. Plan. 2015, 10, 467–486.
- Simunek, J.; van Genuchten, M.T.; Sejna, M. Development and applications of the HYDRUS and STANMOD software packages and related codes. Vadose Zone J. 2008, 7, 587–600.
- Fischione, P.; Celli, D.; Pasquali, D.; Di Risio, M. Drains Inlfuence on the beach groundwater Hydrodynamics. Ital. J. Eng. Geol. Environ. 2020, 2020, 41–47.
- Fischione, P.; Celli, D.; Pasquali, D.; Barajas, G.; Di Paolo, B.; Lara, J.L. Inside a Beach Drainage System: A tridimensional modeling. In Proceedings of the 31st International Ocean and Polar Engineering Conference, Rhodes, Greece, 20–25 June 2021.
- Higuera, P.; Lara, J.L.; Losada, I.J. Three-dimensional interaction of waves and porous coastal structures using OpenFOAM®. Part I: Formulation and validation. Coast. Eng. 2014, 83, 243–258.




