Intermetallic Quasicrystals

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Enrique Maciá Barber	+ 2722 word(s)	2722	2021-12-16 04:17:04	\|
2	format correct	Catherine Yang	Meta information modification	2722	2022-01-10 11:46:12	\|

This entry is adapted from the peer-reviewed paper 10.3390/app9102132

A quasicrystal is the natural extension of the notion of a crystal to structures with quasiperiodic, rather than periodic, translational order. Intermetallic quasicrystals are a class of quasiperiodically ordered solids made of typical metallic atoms, though they do not exhibit the physical properties that usually signal the presence of metallic bonding, and their electrical and thermal transport properties resemble a more semiconductor-like than metallic character. The distribution of atoms throughout the space in these compounds exhibits a characteristic self-similar, scale invariant symmetry, based on a hierarchy of nested atomic clusters.

quasicrystals chemical bond

1. The Chemical Synthesis Route to New Quasicrystals

Elements composing thermodynamically-stable QCs found to date belong to the broad chemical family of metals, including representatives from alkali, alkaline earth, transition metals, or rare-earth blocks ^[1]. By inspecting Figure 1 we see that most main forming elements cluster in groups 11–13 and 4, whereas minority elements are mainly found among TM or RE elements. Thus, most metallic atoms are able to participate in the formation of quasicrystalline phases when one adopts the proper stoichiometric ratios. Indeed, as a matter of fact all of the stable QCs discovered to date have very narrow composition ranges in their respective phase diagrams, indicating that the alloy chemistry strongly affects the stability of these compounds. For instance, the minority atom constituent in the ternary systems

A l 72 P d 17 (R u, O s) 11, A l 63 C u 25 (F e, R u, O s) 15, A l 70 P d 20 (M n, T c, Re) 10, and Zn 60 Mg 30 (Y,Gd,Tb,Dy,Ho,Er) 10, belong to the same group or row of the periodic table, hence indicating the importance of their electronic structure or ionic radii for the stability of the compound, respectively. Similar trends can be observed for the main forming elements as well. For instance, since Cd is located in the same column as Zn in the periodic table, the family of stable i-QCs Cd 65 Mg 20 (Y,Gd,Tb,Dy,Ho,Er,Tm,Yb,Lu,) 15, was obtained by replacing Zn with Cd in the parent i-Zn 50 Mg 42 RE 8 system. Note that the relative content of Mg significantly decreases in the Cd-Mg-RE compounds as compared to the Zn-Mg-RE ones. Since Mg atoms have the smallest ionic radius of all the involved atoms in these alloys, this stoichiometric change may be related to an optimization of the available space in the resulting compounds. Indeed, it is worth noticing that RE elements with atomic radii larger than 1.8 Å apparently do not form stable QCs in the Cd-Mg-RE and Zn-Mg-RE alloy systems, hence suggesting that there exists a restriction on the atomic size in this case. A parameter (referred to as the effective atomic size ratio), has been introduced in order to analyze the role of atomic size effects in QCs’ stability. This parameter takes into account both atomic radius, r α, and concentration, C α, in the form R r,e = (r M C M)/(r A C A), where the subscript A indicates the major constituent, and M stands for secondary or minor elements in the alloy [2] .

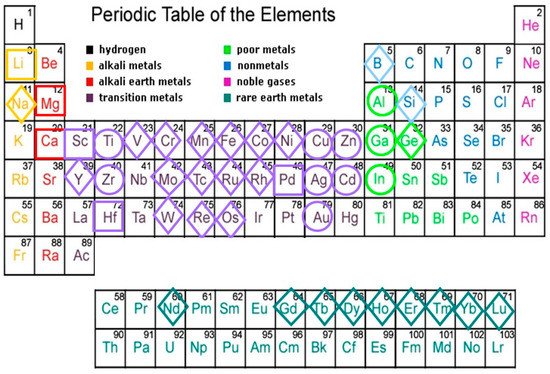
Figure 1. Chemical elements found in thermodynamically-stable QC alloys. Main forming elements (Al, Ga, In, Ti, Zr, Zn, Cd, Cu, Ag, and Au) are circled. The second major constituents are squared. Minor constituents are framed within a diamond.

Substitution of minor constituents by next neighbor elements along a given row in the periodic table has been exploited in order to obtain the family of stable quaternary i-QCs given by the formula Al₇₀Pd₂₀(Mn,Tc,Re)₁₀↦ Al₇₀Pd₂₀(V,Cr,Mo,W)₅(Co,Fe,Ru,Os)₅. The ternary i-QC alloy systems Ag₄₂In₄₂(Yb,Ca)₁₆, and Au₆₅₋₇₀(Si,Ge)₁₆₋₁₉(Gd,Yb)₁₄₋₁₆, were obtained in a similar vein, the former from the parent binary Cd₈₄(Ca,Yb)₁₆ i-QC by replacing Cd atoms by equal amounts of Ag and In ones, which flank Cd element in the periodic table. Finally, it is worth noticing the existence of a great variety of stable i-QCs based on elements belonging to different blocks of the periodic table, but all of them bearing Sc atoms as their second or third constituent (Table 1).

Table 1. Sc bearing icosahedral quasicrystals (i-QCs) belonging to different alloy systems grouped by their electron-per-atom e/a ratio value ^[3]^[2].

Compound	e/a
Zn₈₈Sc₁₂	2.148
Zn_71.5Cu_12.3Sc_16.2	1.797
Cu₄₆Al₃₈Sc₁₆	1.817
$Z n_{74} S c_{16} {(\begin{matrix} A g \\ A u \end{matrix})}_{10}$	1.823 1.822
Zn₇₅Sc₁₆Pd₉	1.829
Zn₇₄Sc₁₆Ni₁₀	1.838
Zn₇₇Sc₁₆Fe₇	1.857
Zn₇₈Sc₁₆Co₆	1.866
Zn₇₄Sc₁₆Pt₁₀	1.885
Al₅₄Pd₃₀Sc₁₆	2.126
Zn₈₁Sc₁₅Mg₄	2.174
$Z n_{77} S c_{8} {(\begin{matrix} H o \\ E r \\ T m \end{matrix})}_{8} F e_{7}$	1.991
Cu₄₈Ga₃₄Sc₁₅Mg₃	2.001

The important role played by the presence of a deep DOS minimum close to the Fermi energy in the stabilization of both icosahedral and decagonal QCs ^[4]^[5]^[6] inspired a chemical synthesis exploration project aimed at obtaining new quasicrystalline compounds via pseudogap electronic tuning, which has rendered successful results in the Zn-Sc-Cu, Ca-Au-In, and Mg-Cu-Ga systems ^[7]^[8]^[9]^[10]. Indeed, for a given alloy composition the Fermi-surface–Brillouin-zone interaction mechanism can give rise to the formation of pseudogaps at energy values that are not close enough to the Fermi energy to significantly contribute to reduce its electronic energy. Now, if that pseudogap occurs above the Fermi energy then one can change the alloy’s composition by properly alloying the original compound with electron-rich atoms in order to change its e/a ratio, shifting E_F to properly match the Fermi level inside the deeper region of the pseudogap. This strategy was systematically applied to different compounds by Corbett and Lin, starting with Zn₁₇Sc₃ alloy (e/a = 2.175) whose structure appeared to be isotypic with that of the prototypic Tsai-type 1/1 approximant. This alloy has an electron concentration ratio larger than that observed in Cd₈₅(Ca,Yb)₁₅ i-QCs (e/a = 2.026), but substitution of some Zn by Cu yields a novel ternary icosahedral phase with the stoichiometry Zn_71.5Sc_16.2Cu_12.3 (e/a = 2.058). The electronic tuning via the compositional change route was subsequently applied to Zn₁₁Mg₂ alloy precursors to get the quaternary i-Cu₄₈Ga₃₄Sc₁₅Mg₃ (e/a = 2.001) phase ^[8], and the ternary i-Zn_82.1Sc_14.6Mg_3.3 (e/a = 2.170) and i-Au_44.2In_41.7Ca_14.1 (e/a = 2.15) compounds ^[7]^[9]. Remarkably enough, the systematic exploration of the active-metal-gold-post-transition-metal Na-Au-Ga system led to the discovery of the first Na-containing QC, i-Ga_37.5Na_32.5Au₃₀, which has a comparatively low e/a ≃ 1.753 value ^[10]. However, the existence of the stable phase i-Au_62.7Al_23.0Ca_14.3 with the even lower e/a ≃ 1.605 value was reported later on ^[11].

2. Assessing the Quasiperiodic Order Role

There are several hints signaling the importance of short-range effects in the emergence of some unusual physical properties of QCs. For instance, electrical conductivity measurements show that (i) amorphous precursors of i-AlCuFe phase already exhibit an increase of conductivity with temperature, and (ii) the structural evolution from the amorphous to the quasicrystalline state is accompanied by a progressive enhancement of the electronic transport anomalies (Figure 2a) ^[12]^[13].

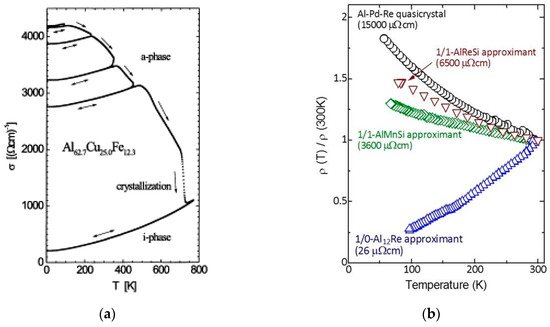
Figure 2. (a) Temperature dependence of the electrical conductivity of an AlCuFe thin film for different annealing states for the amorphous and for the i-QC phase. The conductivity progressively decreases when the long-range order quality is improved (spanning over more than one order of magnitude at low temperatures) and a clear inverse Matthiessen rule is observed in the σ(T) curves. (Reprinted from Haberken, R.; Khedhri, K.; Madel, C.; Häussler, P. Electronic transport properties of quasicrystalline thin films. Mater. Sci. Eng. A 2000, 294-296, 475-480. Copyright (2000), with permission from Elsevier); (b) temperature dependence of the electrical resistivity of a i-AlPdRe QC along with 1/1-AlReSi, 1/1-AlMnSi, and 1/0-Al₁₂Re approximants. The low-temperature electrical resistivity values are indicated in the graph. (Reprinted from Takagiwa, Y.; Kimura, K. Metallic-covalent bonding conversion and thermoelectric properties of Al-based icosahedral quasicrystals and approximants. Sci. Technol. Adv. Mater. 2014, 15, 044802; doi:10.1088/1468-6996/15/4/044802, Creative Commons Atribution-NonCommercial-ShareAlike 3.0 License).

It is worthy noticing that the σ(T) curves reported for both amorphous and QC phases are almost parallel to each other, hence displaying the inverse Matthiessen rule. In an analogous way, crystalline approximants, which exhibit a local atomic environment very similar to their related QC alloys, appear as natural candidates to investigate the relative importance of short-range versus long-range order effects on the transport properties. In fact, many unusual physical properties of QCs are also found in approximant phases, where transport measurements indicate that high-order approximants (say, 1/1 or 2/1), with lattice parameters exceeding about 2 nm, exhibit similar electrical properties to full-fledged QCs, whereas low-order approximants usually display a typically metallic behavior (Figure 2b)^[14]. Furthermore, the observed anomalies are generally more pronounced in the case of QCs. These results indicate that the electronic properties of QCs and their related approximant phases are quite similar, provided that the order of the considered approximants is high enough, thereby guaranteeing the local atomic arrangements are essentially the same, irrespective of the long-range order.

On the contrary, transport properties of metallic alloys with complex unit cells, having a similar number of atomic species to those of approximant phases, but not exhibiting the local isomorphism property characteristic of QCs, are typically metallic instead ^[15]. Therefore, mere structural complexity is not a sufficient condition to give rise to the emergence of anomalous transport properties in QCs. On the other hand, certain anomalous transport properties, such as a high electrical resistivity value or a negative temperature coefficient of electrical resistivity, can also be observed in some crystalline alloys consisting of metallic elements (e.g., Heusler-type Fe₂VAl and Ru₂TaAl alloys) whose structures are unrelated to those of QCs, although both of them share some characteristic features in their electronic structures, namely, a deep and relatively narrow pseudogap close to E_F ^[16]^[17]. Taken together, these observations strongly suggest the importance of short-range effects on the emergence of certain non-metallic properties, which are then appreciably intensified, as long-range QPO progressively pervades the overall structure. In turn, it is tempting to assign a chemical nature to these local effects, probably involving the formation of covalent bonds among certain neighboring atoms.

At this stage it is convenient to highlight that the self-similar symmetry characteristic of fully-fledged QCs has the important effect of reproducing the same local patterns once and again at different spatial scales, thereby relaxing the very notion of “local scale”. In the mathematical literature this property is referred to as local isomorphism and its significant role in interference processes can be described in terms of the so-called Conway’s theorem, which states that distances between identical local arrangements of atoms scale with their own characteristic size ^[18]. That is, any finite-size region reappears once and again in a non-periodic fashion, but always having slightly different surroundings. Thus, the notion of repetitiveness, typical of periodic arrangements, should be replaced by that of local isomorphism, which expresses the occurrence of any bounded region of the structure infinitely often across the whole volume. In the particular cases of Fibonacci chain and Penrose tiling, Conway’s theorem states that given any local pattern having a certain characteristic length, L, at least one identical pattern can be found within a distance of 2L, as it is illustrated in Figure 3.

Figure 3. Illustration of Conway’s theorem in a Penrose tiling: Given an arbitrary pattern of tiles (indicated by L in the picture) one will always find a replica of it at a distance smaller than twice its length (dashed circle).

Therefore, the physical reason for the presence of so many reflections in the diffraction spectra of QCs is a direct consequence of QPO, which guarantees the existence of suitable interference conditions at multiple scales. In the same vein, the existence of critical wave functions with a recurrent spatial pattern in QCs is closely related to the competition between local isomorphism and long-range QP order. Thus, the absence of periodicity favors the localization of the wave function in a local pattern. However, according to Conway’s theorem this local pattern must have duplicates that extend throughout the whole structure. Then, quantum resonances between such localized states at identical local configurations favor a tunneling effect which gives rise to a hopping mechanism. As a result, the wave functions become more extended in nature, ultimately resulting in electronic and phonon states exhibiting a self-similar structure, in the sense that certain portions of the wave function amplitudes, extending over identical configurations, only differ by a scale factor. In summary, the presence of self-similar symmetry in QCs structures renders the difference between short-range and long-range scales, to which we are so used to in the study of periodic structures, somewhat fuzzy, as their overall architecture can be regarded as a hierarchical arrangement of certain basic building blocks at different scales.

3. Quasicrystals as Cluster Aggregates

These building units generally adopt well-defined polyhedral shapes and can be described as regular arrangements of atoms in nested shells adopting point group icosahedral symmetries (dodecahedron, icosahedron, triacontahedron, icosidodecahedron). By attending the detailed structure of these polyhedral i-QCs, they can be classified into three main classes, namely: (1) The AlMnSi class, whose prototype is given by the α-Mn₁₂(Al,Si)₅₇ phase; (2) the MgAlZn class, whose prototype is given by the Mg₃₂(Al,Zn)₄₉ Bergman phase; and (3) the CdYb class, whose prototype is given by the Cd₆Yb phase. In all cases the entire self-similar atomic structure can be obtained starting from a given polyhedral seed by systematically applying an inflation process via successive substitutions of atoms by clusters. The inflation operation consists of a proper rescaling by a scale factor τ³, where τ = (1 + √5)/2 is the so-called golden mean. An example of the resulting structure is shown in Figure 4b, displaying an icosidodecahedral aggregate consisting of icosidodecahedral atomic clusters.

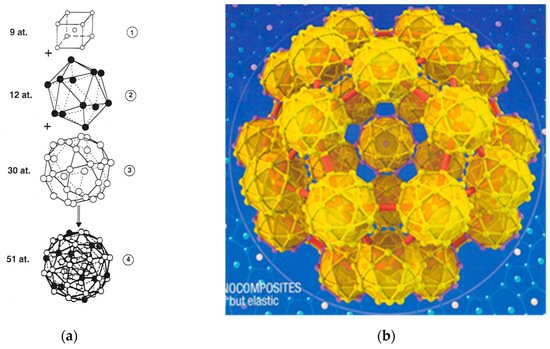
Figure 4. (a) Structure of a pseudo-Mackay cluster containing an inner cubic shell (1), followed by an icosahedron shell (2), and an icosidodecahedron (3) shell. The number of atoms in each shell is indicated in the figure. White (black) circles denote Al (TM) atoms, respectively. (Reprinted figure with permission from Janot, C. Conductivity in quasicrystals via hierarchically variable-range hopping. Phys. Rev. B 1996, 53, 181. Copyright (1996) by the American Physical Society); (b) A three-dimensional perspective of the τ³-inflated cluster forming the basic icosidodecahedron structural motif of i-CdYb phase. Its radius is about 12 nm. (Reprinted by permission from Springer Nature: Nature Materials, Takakura, H.; Pay-Gómez, C.; Yamamoto, A.; de Boissieu, M.; Tsai, A. P. Atomic structure of the binary icosahedral Yb-Cd quasicrystal. 2007, 6, 58-63, Copyright (2007)).

As it is deduced from X-ray and neutron diffraction data the structure of i-AlPdMn and i-AlCuFe QCs is based on the so-called pseudo-Mackay cluster, which contains 51 atoms and can be described in terms of three centrosymmetric atomic shells: A core of nine atoms, an intermediate icosahedron of 12 atoms, and an external icosidodecahedron of 30 atoms (Figure 4a) ^[19]^[20]^[21]^[22]. The structures of stable i-QCs in the AlCuLi, ZnMgZr, ZnMgRE, ZnMg(Al,Ga) and MgAlPd systems were grouped in the MgAlZn class, which is based on the so-called Bergman clusters: The center is vacant, the first shell is an Al/Zn icosahedron, the second shell is a Mg dodecahedron, and the third shell is a larger Al/Zn icosahedron. Finally, stable i-QCs found in the binary Cd(Yb,Ca) and the ternary ZnScM, (Ag,Au)In(Yb,Ca), and CdMgRE alloy systems have been grouped in the CdYb Tsai-cluster third class, which constitutes the largest of the three classes of i-QCs. In the core of each Tsai-type cluster there is a tetrahedron created by four positionally-disordered Cd atoms, the first shell is a Cd dodecahedron, the second shell is a Yb icosahedron, and the third shell is a Cd icosidodecahedron ^[23]^[24] (Figure 4b).

A major question in the field is whether clusters are physically-significant, chemically-stable entities, or simply convenient geometrical constructions. A number of evidences supporting the existence of clusters as stable physicochemical entities have been reported in the literature, including secondary electron imaging ^[25], X-ray photoelectron diffraction ^[26], and scanning tunneling microscopy techniques ^[27]. The obtained results support the picture of i-QCs as cluster aggregates, which can be described in terms of a three-dimensional QP lattice properly decorated by atomic clusters having the same point symmetry as the whole QC ^[28]. This scenario naturally brings about some questions, which are the focus of intensive current research. For example, a given cluster may act as a chemically-stable structure when isolated, but it may lose its identity, due to strong interactions with close neighbors, when assembled to form a solid. So, what is the nature of the chemical bonding among the atoms belonging to a given cluster, as well as among different clusters themselves? Then, along with the stability of clusters we should also consider those aspects related to their reactivity. In a similar way, one may wonder about the number and structure of the different atomic clusters compatible with the system’s stoichiometry, or regarding the more appropriate packing rules involving atomic clusters at different hierarchical stages.

References

Maciá-Barber E. Quasicrystals: Fundamentals and Applications; CRC Pres, Taylor & Francis: Boca Raton, FL, 2021; pp. 1-58.
Cui, C.; Shimoda, M.; Tsai, A.P. Studies on icosahedral Ag-In-Yb: A prototype for Tsai-type quasicrystals. RSC Adv. 2014, 4, 46907–46921.
Steurer, W.; Deloudi, S. Crystallography of Quasicrystals—Concepts, Methods and Structures; Springer Series in Materials Science 126; Springer: Berlin, Germany, 2009.
Zhang, D. Electronic properties of stable decagonal quasicrystals. Phys. Status Solidi A 2010, 207, 2666–2673.
Belin-Ferré, E. Electronic structure in quasicrystalline compounds and related crystals. J. Phys. Condens. Matter 2002, 14, R789–R816.
Nakayama, K.; Mizutani, A.; Koyama, Y. Crystallographic features and state stability of the decagonal quasicrystal in the Al-Cu-Co alloy system. J. Phys. Soc. Jpn. 2016, 85, 114602.
Lin, Q.; Corbett, J.D. New stable icosahedral quasicrystalline phase in the Sc-Cu-Zn system. Philos. Mag. Lett. 2003, 83, 755–762.
Lin, Q.; Corbett, J.D. Electronic tuning of MgCuGa. A route to crystalline approximant and quasicrystalline phases. J. Am. Chem. Soc. 2005, 127, 12786–12787.
Lin, Q.; Corbett, J.D. Development of the Ca-Au-In icosahedral quasicrystal and two crystalline approximants: Practice via pseudogap electronic tuning. J. Am. Chem. Soc. 2007, 129, 6789–6797.
Lin, Q.; Corbett, J.D. A chemical approach to the discovery of quasicrystals and their approximant crystals. In Controlled Assembly and Modification of Inorganic Systems; Springer: Berlin/Heidelberg, Germany, 2009; Volume 133, pp. 1–39.
Smetana, V.; Lin, Q.; Pratt, D.K.; Kreyssig, A.; Ramazanoglu, M.; Corbett, J.D.; Goldman, A.I.; Miller, G.J. A sodium-containing quasicrystal: Using gold to enhance sodium’s covalency in intermetallic compounds. Angew. Chem Int. Ed. 2012, 51, 12699–12702.
Pham, J.; Meng, F.; Lynn, M.J.; Ma, T.; Kreyssig, A.; Kramer, M.J.; Goldman, A.I.; Miller, G.J. From quasicrystals to crystals with interpenetrating icosahedra in Ca-Au-Al: In situ variable-temperature transformation. J. Am. Chem. Soc. 2018, 140, 1337–1347.
Haberken, R.; Khedhri, K.; Madel, O.; Häussler, P. Electronic transport properties of quasicrystalline thin films. Mater. Sci. Eng. A 2000, 294–296, 475–480.
Yoshiki Takagiwa; Kaoru Kimura; Metallic–covalent bonding conversion and thermoelectric properties of Al-based icosahedral quasicrystals and approximants. Science and Technology of Advanced Materials 2014, 15, 044802, 10.1088/1468-6996/15/4/044802.
Roth, C.; Schwalbe, G.; Knöfler, R.; Zavaliche, F.; Madel, O.; Haberken, R.; Häussler, P. A detailed comparison between the amorphous and the quasicrystalline state of Al-Cu-Fe. J. Non-Cryst. Solids 1999, 252, 869–873.
Tseng, C.W.; Kuo, C.N.; Lee, H.W.; Chen, K.F.; Huang, R.C.; Wei, C.-M.; Kuo, Y.K.; Lue, C.S. Semimetallic behavior in Heusler-type Ru2TaAl and thermoelectric performance improved by off-stoichiometry. Phys. Rev. B 2017, 96, 125106.
Nishino, Y. Electronic structure and transport properties of pseudogap system Fe2VAl. Mater. Trans. 2001, 42, 902–910.
Gardner, M. Extraordinary nonperiodic tiling that enriches the theory of tiles. Sci. Am. 1977, 236, 110–117.
Boudard, M.; de Boissieu, M. Experimental determination of the structure of quasicrystals. In Physical Properties of Quasicrystals, 2nd ed.; Stadnik, Z.M., Ed.; Springer Series in Solid-State Sciences; Springer: Berlin, Germany, 1999; Volume 126, pp. 91–126.
Janot, C.; de Boissieu, M. Quasicrystals as a hierarchy of clusters. Phys. Rev. Lett. 1994, 72, 1674–1677.
Janot, C. Conductivity in quasicrystals via hierarchically variable-range hopping. Phys. Rev. B 1996, 53, 181–191.
Janot, C.J. Atomic clusters, local isomorphism, and recurrently localized states in quasicrystals. J. Phys. Condens. Matter 1997, 9, 1493–1508.
Takakura, H.; Pay-Gómez, C.; Yamamoto, A.; de Boissieu, M.; Tsai, A.P. Atomic structure of the binary icosahedral Yb-Cd quasicrystal. Nat. Mater. 2007, 6, 58–63.
Tsai, A.P. Icosahedral clusters, icosahedral order and stability of quasicrystals—A view of metallurgy. Sci. Technol. Adv. Mater. 2008, 9, 013008.
Zurkirch, M. Critical test for the icosahedral structure of the quasicrystal Al70Pd20Mn10. Philos. Mag. Lett. 1996, 73, 107–114.
Naumovic, D.; Aebi, P.; Schlapbach, L.; Beeli, C. A real-space and chemically-sensitive study of the i-AlPdMn pentagonal surface. In New Horizons in Quasicrystals-Research and Applications; Goldman, A.I., Sordelet, D.J., Thiel, P.A., Dubois, J.M., Eds.; World Scientific: Singapore, 1997; pp. 86–94.
Ebert, P.H.; Feuerbacher, M.; Tamura, N.; Wollgarten, M.; Urban, K. Evidence for a cluster-based structure of AlPdMn single quasicrystals. Phys. Rev. Lett. 1996, 77, 3827.
Abe, E.; Yan, Y.; Pennycook, S.J. Quasicrystals as cluster aggregates. Nat. Mater. 2004, 3, 759–767.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Physics, Condensed Matter

Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Enrique Maciá Barber

View Times: 506

Update Date: 10 Jan 2022

Table of Contents

Video Upload Options

Confirm

1. The Chemical Synthesis Route to New Quasicrystals

2. Assessing the Quasiperiodic Order Role

3. Quasicrystals as Cluster Aggregates

References