Process Intensification

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Jesús Rafael Alcántara-Ávila	+ 1686 word(s)	1686	2021-11-29 07:09:30	\|
2	format correct	Catherine Yang	Meta information modification	1686	2021-12-09 03:57:21	\|

This entry is adapted from the peer-reviewed paper 10.3390/pr9122150

Process Intensification (PI) is a vast and growing area in Chemical Engineering, which deals with the enhancement of current technology to enable improved efficiency; energy, cost, and environmental impact reduction; small size & modularization; and better integration with the other equipment. Since process intensification results in novel, but complex, systems, it is necessary to rely on optimization and control techniques that can cope with such new processes.

process intensification process control process synthesis optimization

1. Introduction

The pioneering work from Stankiewicz and Moulijn ^[1] is undoubtedly the most referenced work that defines Process Intensification (PI). Here, it was defined as “any chemical engineering development that leads to a substantially smaller, cleaner, and more energy-efficient technology”. Later, more definitions appeared over time because PI has grown to consider more processes, units, and phenomena. PI was also defined as adding/enhancing phenomena in a process through the integration of operations, functions, phenomena or alternatively through the targeted enhancement of phenomena in an operation ^[2], any activity which enables smaller equipment for a given throughput, higher throughput for a given equipment size or process, less holdup for equipment or less inventory for process of certain material for the same throughput, less usage of utility materials, and feedstock for a given throughput and a given equipment size, and higher performance for a given unit size ^[3]. In addition, the authors classified PI into two main categories, which are unit intensification and plant intensification. The former aims to intensify a single pre-specified unit alone, and the latter aims to intensify more than one unit simultaneously. Stankiewicz et al. clustered the approaches to PI into four domains: structure (spatial), energy (thermodynamic), functional (synergy), and temporal (time) domains ^[4].

PI has been also applied for the miniaturization of processes, which are material and shape dependent. Plant miniaturization focuses on modular flexibility, shorter lead-time for fine chemicals, and the use of renewable energy sources. Other PI examples such as microwave reactors, fine bubble generation devices, rotating packed bed reactors, microreactors, electric fields, plasma technologies, and membrane-based separations are not so easy to model mathematically or to simulate because their performances are highly dependent on the size and shape of the devices and the operating flow rate and target systems. In addition, detailed and accurate mathematical models are not always available for such developing technologies. Thus, the research and development of these process intensifications are highly device and material oriented.

2. Process Synthesis and Optimization

Advancements in PI come together with advancements in Process Synthesis (PS) and Process Optimization (PO) ^[5]. Although process synthesis, integration, and intensification focus on improving the performance of chemical processes in terms of energy efficiency, sustainability, and economic profitability, there are several differences between these approaches. Traditional process synthesis operates at the equipment and flowsheet scales; process integration deals with plant-scale decisions, material/energy redistribution, and utility networks. Process intensification, on the other hand, seeks for enhancements at the fundamental physicochemical phenomena scale to generate novel equipment and flowsheet alternatives ^[6].

2.1. Process Synthesis

Process synthesis aims to screen flowsheet variants, equipment types, operating conditions, and equipment connectivity under several designs and operational constraints ^[6]. Process synthesis aims to find the best processing route, from among numerous alternatives, to convert given raw materials to specific (desired) products, subject to predefined performance criteria. Hence, process synthesis involves analyzing the problem and generating, evaluating, and screening process alternatives to later decide the best process option. Process synthesis is usually performed through the following three methods: (1) rule-based heuristic methods, which are defined from process insights and know-how; (2) mathematical programming-based methods, where the best flowsheet alternative is determined from network superstructure optimization (this method is useful when the system is well-defined, and many combinations of alternatives are considered); and (3) hybrid methods, which use process insights, know-how, rules, and mathematical programming; that is, models are used to obtain good physical insights that aid in reducing the search space of alternatives so that the synthesis problem to be solved will involve less alternatives ^[7]. Thus, the fundamental goal of process synthesis is the invention of detailed processing routes at the desired scale, safely, environmentally responsibly, efficiently, and economically, in a manner that is superior to all other possible processes ^[8].

2.2. Process Optimization

The optimization approaches can be purely mathematical, in which optimization problems are represented explicitly by equations, or it can be combined with process simulation, where some constraints are implicitly solved. In both cases, the optimization problems can be solved deterministically or stochastically.

The concept of simulation-based optimization can also be applied to randomized, derivative-free optimization methods (e.g., Neural Network Algorithms (NNA), Simulated Annealing (SA), and Particle Swarm Optimization (PSO)). The sequential iterative (SI) approach has been used widely for determining the optimal design parameters ^[9]. However, SA and the genetic algorithm (GA) have been used as optimization approaches because they can be programmed easily and can find optimal solutions quickly due to their computerized natures. Some studies demonstrated that the use of these optimization techniques resulted in a Total Annual Cost (TAC) lower than that obtained in exhaustive trial-and-error simulations. For example, Yang and Ward ^[10] proposed an optimization framework that combined process simulation as an automation server and an SA algorithm written in MATLAB ^[11] for the separation of three different mixtures through extractive distillation (ED). Recently, SA was also used for the optimization of ED sequences with side streams ^[12]. GA has been used for the optimization of a Reactive Distillation (RD) and ED sequence using a multi-objective optimization framework considering economic and environmental criteria ^[13], and in RD and pressure-swing distillation (PSD) ^[14]. In these works, the reported TAC using SA or GA was lower than that obtained using the SI approach.

Christopher et al. proposed a simulation-based optimization framework for the intensification of Propylene/Propane separation involving mechanical vapor recompression (MVR) and self-heat recuperation (SHR) for the synthesis of four distillation-based configurations ^[15]. The TAC was minimized for each configuration. The simulation-based optimization framework combined Aspen HYSYS as the process simulator and PSO in MATLAB as the optimizer. The simulation-based optimization framework was shown to be beneficial because all thermodynamic calculations could be performed in a process simulator, while rigorous optimization algorithms could be implemented in an external software.

3. Process Control

Process Innovation is intrinsically connected to process optimization and control. Thus, it is important to propose optimization methodologies to tackle current and future challenging processes. Presently, process flow sheets are evaluated in a sequential fashion where they are first generated and their resulting design is analyzed considering its (1) dynamic behavior, (2) flexibility, (3) robustness, and (4) controllability. Typically, control schemes are designed after the process is synthesized and optimized ^[8].

Figure 1 summarizes the typical procedure for evaluating the control performance of process flowsheets. The evaluation generally consists of two steps, which are steady-state simulation and dynamic simulation. The steady-state simulation involved in flowsheet development is commonly performed using Aspen Plus software. After the initial flowsheet has been developed, the design parameters are optimized to obtain the TAC to determine the best design. Following this, all the related equipment in the optimized flowsheet (i.e., the best design) are sized accordingly, and appropriate pressure drops are implemented across the flowsheet so that it can be converted into a pressure-driven simulation for further dynamic assessment. Inventory control loops are installed during the dynamic simulation after various techniques determine the sensitive tray temperature location. Finally, quality control loops are installed before the system is tested with various disturbances such as feed flowrate and composition disturbances.

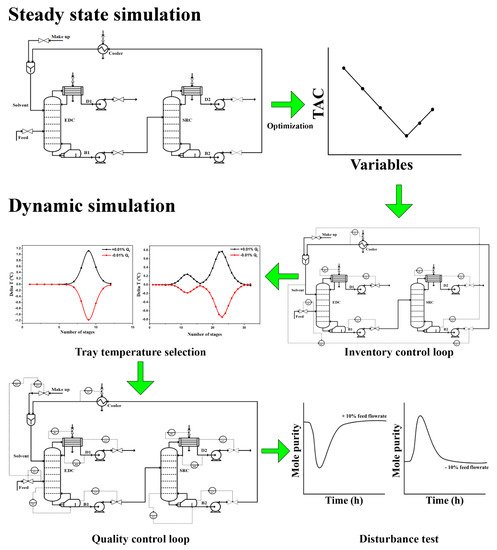
Figure 1. General procedures for evaluating process flowsheets.

Generally, the control structures are divided into two parts, which are inventory control loops and quality control loops. Inventory control loops help to maintain material balance stability of the overall plant and provide effective operation control during disturbances while quality control loops keep the product purities at their desired specification, and they are usually installed after inventory control loops.

Two types of control strategies are commonly used, i.e., the composition control [92,93] or the tray temperature control [94]. In some complicated processes, a hybrid control strategy (e.g., composition to temperature cascade control) is employed to keep the product at its desired purity [95,96].

4. Simultaneous Design and Control

Burnak et al. presented a very informative paper about the last five decades of model-based design optimization techniques to solve the simultaneous consideration of process design, scheduling, and control ^[16]. Since process design, scheduling, and control problems are traditionally constructed to address different objectives, and they span widely different time scales, it is challenging to evaluate and determine the optimal trade-off between different decision-makers systematically. Despite the efforts to simultaneously design and control a process, significant assumptions and simplifications must still be made regarding the operational decisions in the process design step.

Aneesh et al. presented an excellent review on the simultaneous design and control of intensified distillation processes because such processes are nonlinear in nature, and highly integrated with more than one interconnected piece of equipment ^[17]. Thus, the conventional sequential design-control approach may lead to poor dynamic operability in the case of external disturbances and uncertainties. Therefore, the optimal performance of the process requires the improvement of the performance and dynamic characteristics together with the process design. The sequential design-control approach imposes restrictions on the flexibility (i.e., the ability of the process to move from one operating point to another), the feasibility (i.e., the ability of the system to operate under allowable limits in the presence of parameter uncertainties, and time-varying disturbances), and the controllability of the process since the optimal process design, obtained at steady-state, may limit, or may not satisfy, the minimum performance requirements specified for this process when the system is operated in the transient mode ^[18]. In addition, the sequential design-control approach has typically been based on the assumption of operation around a nominal steady-state point, while its dynamic performance has been primarily evaluated through disturbance rejection. However, chemical plants presently operate in an environment of increased competition in a global marketplace, with increased variation in product demand and raw material supply. The deregulation of electricity prices in many jurisdictions has also resulted in large fluctuations in electricity prices. Therefore, it is becoming increasingly important for plants to be able to transition rapidly to respond to such variation to maximize profits and increase competitiveness ^[19].

References

Stankiewicz, A.I.; Moulijn, J.A. Process Intensification: Transforming Chemical Engineering. Chem. Eng. Prog. 2000, 96, 22–34.
Lutze, P.; Gani, R.; Woodley, J.M. Process intensification: A perspective on process synthesis. Chem. Eng. Process. Process Intensif. 2010, 49, 547–558.
Ponce-Ortega, J.M.; Al-Thubaiti, M.M.; El-Halwagi, M.M. Process intensification: New understanding and systematic approach. Chem. Eng. Process. Process Intensif. 2012, 53, 63–75.
Stankiewicz, A.I.; Gerven, T.V.; Stefanidis, G. The Fundamentals of Process Intensification, 1st ed.; Wiley-VCH: Weinheim, Germany, 2019; ISBN 3527327835.
Sitter, S.; Chen, Q.; Grossmann, I.E. An overview of process intensification methods. Curr. Opin. Chem. Eng. 2019, 25, 87–94.
Demirel, S.E.; Li, J.; Hasan, M.M.F. A General Framework for Process Synthesis, Integration, and Intensification. Ind. Eng. Chem. Res. 2019, 58, 5950–5967.
Babi, D.K.; Holtbruegge, J.; Lutze, P.; Gorak, A.; Woodley, J.M.; Gani, R. Sustainable process synthesis-intensification. Comput. Chem. Eng. 2015, 81, 218–244.
Barnicki, S.D.; Siirola, J.J. Process synthesis prospective. Comput. Chem. Eng. 2004, 28, 441–446.
Tang, Y.T.; Chen, Y.W.; Huang, H.P.; Yu, C.C.; Hung, S.B.; Lee, M.J. Design of reactive distillations for acetic acid esterification. AIChE J. 2005, 51, 1683–1699.
Yang, X.L.; Ward, J.D. Extractive Distillation Optimization Using Simulated Annealing and a Process Simulation Automation Server. Ind. Eng. Chem. Res. 2018, 57, 11050–11060.
MathWorks MATLAB. The Language of Technical Computing. Available online: https://www.mathworks.com/help/matlab/ (accessed on 24 October 2021).
Cui, Y.; Zhang, Z.; Shi, X.; Guang, C.; Gao, J. Triple-column side-stream extractive distillation optimization via simulated annealing for the benzene/isopropanol/water separation. Sep. Purif. Technol. 2020, 236, 116303.
Su, Y.; Yang, A.; Jin, S.; Shen, W.; Cui, P.; Ren, J. Investigation on ternary system tetrahydrofuran/ethanol/water with three azeotropes separation via the combination of reactive and extractive distillation. J. Clean. Prod. 2020, 273, 123145.
Yang, A.; Su, Y.; Teng, L.; Jin, S.; Zhou, T.; Shen, W. Investigation of energy-efficient and sustainable reactive/pressure-swing distillation processes to recover tetrahydrofuran and ethanol from the industrial effluent. Sep. Purif. Technol. 2020, 250, 117210.
Christopher, C.C.E.; Dutta, A.; Farooq, S.; Karimi, I.A. Process Synthesis and Optimization of Propylene/Propane Separation Using Vapor Recompression and Self-Heat Recuperation. Ind. Eng. Chem. Res. 2017, 56, 14557–14564.
Burnak, B.; Diangelakis, N.A.; Pistikopoulos, E.N. Towards the grand unification of process design, scheduling, and control-utopia or reality? Processes 2019, 7, 461.
Aneesh, V.; Antony, R.; Paramasivan, G.; Selvaraju, N. Distillation technology and need of simultaneous design and control: A review. Chem. Eng. Process. Process Intensif. 2016, 104, 219–242.
Ricardez-Sandoval, L.A. Optimal design and control of dynamic systems under uncertainty: A probabilistic approach. Comput. Chem. Eng. 2012, 43, 91–107.
Swartz, C.L.E.; Kawajiri, Y. Design for dynamic operation—A review and new perspectives for an increasingly dynamic plant operating environment. Comput. Chem. Eng. 2019, 128, 329–339.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Engineering, Chemical

Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Jesús Rafael Alcántara-Ávila

View Times: 1.8K

Update Date: 09 Dec 2021

Table of Contents

Video Upload Options

Confirm