
| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Luigi Di Sarno | + 2590 word(s) | 2590 | 2021-11-30 06:46:42 | | | |
| 2 | Bruce Ren | Meta information modification | 2590 | 2021-12-07 09:49:25 | | | | |
| 3 | Lindsay Dong | Meta information modification | 2590 | 2022-03-28 07:31:13 | | |
Video Upload Options
Atmospheric corrosion can seriously affect the performance of steel structures over long periods of time; thus, it is essential to evaluate the rate of corrosion and subsequent modification of dynamic properties of a structure over different time periods. Standards and codes represent the general guidelines and suggest general protection techniques to prevent structures from corrosion damage.
1. Introduction
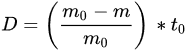 (1)
(1)| Corrosivity Categories | Corrosivity | Typical Outdoor Atmospheric Environments |
|---|---|---|
| C1 | Very low | Dry or cold zone with very low pollution and TOW * e.g., deserts, Antarctic zone |
| C2 | Low | Temperate zone with low pollution (SO2 (μg/m3) < 5), e.g., rural areas. |
| Dry and cold zone with short TOW, e.g., deserts and subarctic areas | ||
| C3 | Medium | Temperate zone with medium pollution (5 < SO2 (μg/m3) < 30) and low chloride effect, e.g., urban areas and coastal areas with low concentration of chloride ions Subtropical and tropical zones with low pollution |
| C4 | High | Temperate zone with high pollution (30 < SO2 (μg/m3) < 90) or considerable effect of chlorides, e.g., polluted urban areas, industrial areas, coastal areas without spray of salt water or, de-icing salts influences Subtropical and tropical zone with medium pollution |
| C5 | Very high | Temperate zones with high pollution levels (90 < SO2 (μg/m3) < 250); high chloride deposition rates, e.g., industrial areas, coastal and sea zones and sheltered positions on coastline. |
| CX | Extreme | Subtropical and tropical zone with significant TOW, atmospheric environment with very high level of SO2 deposits (SO2 (μg/m3) > 250) including accompanying and production factors with profound effect of chloride concentration, e.g., extreme industrial areas, coastal areas and contact with salt spray |
2. Corrosion of Metals

-
Uniform corrosion: generating a uniform layer of rust (formation of oxide) over the surface of the metal exposed to atmosphere. In principle, uniform corrosion can reduce the rate of corrosion by limiting the contact surface between metal and the atmosphere. This is the most common type of corrosion in steel bridges.
-
Galvanic corrosion: When two metals with different corrosive potential are placed together with the presence of a corrosive environment (electrolyte), the current flow and hence corrosion damage occur.
-
Pitting Corrosion: One of the most common forms of corrosion with local attack which sometimes taking the form of deep holes (pits) into steel surface. This kind of corrosion in the presence of imperfection in steel components or dirt on its surface can engender cracks into the metal surface.
-
Crevice Corrosion: This type of localized corrosion occurs by the differences between ion concentration in dissimilar environments (different ion concentration) inside and outside of the small crevice.
-
Erosion Corrosion: When flowing of fluid with the relatively high velocity attacks over the surface of the metal, it can remove the coating film and accelerate the corrosion process.
-
Stress Corrosion: In the presence of corrosive environment and applied tensile stress, brittle cracking occurs into the metal.
-
Fatigue Corrosion: Repeated applied load with the corrosive environment causes stress concentration which leads to cracks into the metal.
-
Fitting Corrosion: When two surfaces are in close contact in the presence of load provoke the abrasion of the surfaces by oxide.
-
Intergranular Corrosion: The corrosion attack between steel grain boundaries which affect the mechanical properties of the material.

3. Corrosion Modeling
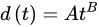 (2)
(2)
 (3)
(3)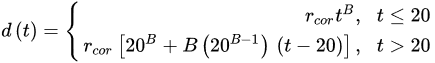 (4)
(4)where rcor is the corrosion rate in the first year of exposure in grams per square meter per year (g/(m2·yr)) or micrometer per year (μm/year) consistent with ISO9223 [13]. Adjustment work reported by Albrecht and Hall Jr in 2003 [23] where the steady-state point was modified to subsequent years after the first year of exposure (instead of year 10 in Equation (3)). A nonlinear time-dependent model was recommended by Soares and Garbatov [24] in 1999, was separated into three main parts (Figure 3). At the first stage (OA) there is no corrosion due to the presence of protection layer. The second part (AB) is the initiation of corrosion because of damage to coating layer. The slope of the plot (corrosion rate) decreases until the corroded layer appears on the entire element surface (zero corrosion rate at C). This model can be utilized in different environmental conditions (Equation (5)) and it holds that:
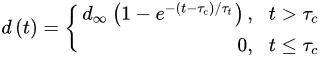 (5)
(5)
where τc is coating life, d∞ is the long-term thickness of the corroded component and τt is transition time which is calculated as d∞/tg∝.

 (6)
(6)
References
- Koch, G.; Varney, J.; Thompson, N.; Moghissi, O.; Gould, M.; Payer, J. International Measures of Prevention, Application, and Economics of Corrosion Technologies Study; NACE International: Houston, TX, USA, 2016; p. 3.
- Di Lorenzo, G.; Landolfo, R. Sensitivity study of dynamics variability for mild-carbon steel structures affected by corrosion. Open Constr. Build. Technol. J. 2019, 13, 251–268.
- Xu, S.; Wang, H.; Li, A.; Wang, Y.; Su, L. Effects of corrosion on surface characterization and mechanical properties of butt-welded joints. J. Constr. Steel Res. 2016, 126, 50–62.
- Ma, Y.; Li, Y.; Wang, F. The atmospheric corrosion kinetics of low carbon steel in a tropical marine environment. Corros. Sci. 2010, 52, 1796–1800.
- Wang, H.; Wang, Y.; Zhang, Z.; Liu, X.; Xu, S. Cyclic behavior and hysteresis model of beam-column joint under salt spray corrosion environment. J. Constr. Steel Res. 2021, 183, 106737.
- Wang, H.; Xu, S.; Li, A.; Kang, K. Experimental and numerical investigation on seismic performance of corroded welded steel connections. Eng. Struct. 2018, 174, 10–25.
- Xu, S.; Zhang, Z.; Qin, G. Study on the seismic performance of corroded H-shaped steel columns. Eng. Struct. 2019, 191, 39–61.
- Zhang, X.; Zheng, S.; Zhao, X. Experimental and numerical study on seismic performance of corroded steel frames in chloride environment. J. Constr. Steel Res. 2020, 171, 106164.
- Di Lorenzo, G.; Rizzo, F.; Formisano, A.; Landolfo, R.; Guastaferro, A. Corrosion wastage models for steel structures: Literature review and a new interpretative formulation for wrought iron alloys. In Key Engineering Materials; Trans Tech Publications Ltd.: Freienbach, Switzerland, 2019; Volume 813, pp. 209–214.
- Landolfo, R.; Cascini, L.; Portioli, F. Modeling of metal structure corrosion damage: A state of the art report. Sustainability 2010, 2, 2163–2175.
- Rizzo, F.; Di Lorenzo, G.; Formisano, A.; Landolfo, R. Time-dependent corrosion wastage model for wrought iron structures. J. Mater. Civ. Eng. 2019, 31, 04019165.
- Da Silva, L.S.; Simões, R.; Gervásio, H. Design of Steel Structures: Eurocode 3: Design of Steel Structures—Part 1-1: General Rules and Rules for Buildings; European Convention for Constructional Steelwork (ECCS): Brussels, Belgium, 2010.
- ISO. Corrosion of Metals and Alloys—Corrosivity of Atmospheres—Classification, Determination and Estimation; ISO 9223; International Organization for Standardization: Geneva, Switzerland, 2012.
- Popov, B.N. Corrosion Engineering: Principles and Solved Problems; Elsevier: Amsterdam, The Netherlands, 2015.
- Kulicki, J.; Prucz, Z.; Sorgenfrei, D.; Mertz, D.; Young, W. Guidelines for Evaluating Corrosion Effects in Existing Steel Bridges; Transportation Research Board: Washington, DC, USA, 1990.
- Simillion, H.; Dolgikh, O.; Terryn, H.; Deconinck, J. Atmospheric corrosion modeling. Corros. Rev. 2014, 32, 73–100.
- Benarie, M.; Lipfert, F.L. A general corrosion function in terms of atmospheric pollutant concentrations and rain pH. Atmos. Environ. 1986, 20, 1947–1958.
- Feliu, S.; Morcillo, M.; Feliu, S., Jr. The prediction of atmospheric corrosion from meteorological and pollution parameters—I. Annual corrosion. Corros. Sci. 1993, 34, 403–414.
- Feliu, S.; Morcillo, M.; Feliu, S., Jr. The prediction of atmospheric corrosion from meteorological and pollution parameters—II. Long-term forecasts. Corros. Sci. 1993, 34, 415–422.
- ISO. Corrosion of Metals and Alloys—Corrosivity of Atmospheres—Guiding Values for the Corrosivity Categories; ISO 9224; International Organization for Standardization: Geneva, Switzerland, 1992.
- ISO. Corrosion of Metals and Alloys–Corrosivity of Atmospheres–Classification, Determination and Estimation; ISO 9224; International Organization for Standardization: Geneva, Switzerland, 2012.
- Panchenko, Y.M.; Marshakov, A. Long-term prediction of metal corrosion losses in atmosphere using a power-linear function. Corros. Sci. 2016, 109, 217–229.
- Albrecht, P.; Hall, T.T., Jr. Atmospheric corrosion resistance of structural steels. J. Mater. Civ. Eng. 2003, 15, 2–24.
- Soares, C.G.; Garbatov, Y. Reliability of maintained, corrosion protected plates subjected to non-linear corrosion and compressive loads. Mar. Struct. 1999, 12, 425–445.
- Paik, J.K.; Kim, S.K.; Lee, S.K. Probabilistic corrosion rate estimation model for longitudinal strength members of bulk carriers. Ocean. Eng. 1998, 25, 837–860.
- Qin, S.; Cui, W. Effect of corrosion models on the time-dependent reliability of steel plated elements. Mar. Struct. 2003, 16, 15–34.
- Klinesmith, D.E.; McCuen, R.H.; Albrecht, P. Effect of environmental conditions on corrosion rates. J. Mater. Civ. Eng. 2007, 19, 121–129.
- MATLAB and Statistics Toolbox Release 2021a; The MathWorks, Inc.: Natick, MA, USA, 2021.




