Magnetic Elements for Neuromorphic Computing

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Tomasz BLACHOWICZ	+ 1561 word(s)	1561	2021-11-17 10:51:32	\|
2	format correction	Peter Tang	+ 30 word(s)	1591	2021-11-30 02:09:52	\| \|
3	the order of authors has been changed	Tomasz BLACHOWICZ	Meta information modification	1591	2021-12-01 09:08:55	\|

This entry is adapted from the peer-reviewed paper 10.3390/molecules25112550

Neuromorphic computing is also called cognitive or adaptive computing. Brain-inspired computers could work like neuronal networks, be more energy-efficient, and could learn and solve special mathematical problems faster than recent computers. It is assumed to be significantly more energy efficient than, and at the same time expected to outperform, conventional computers in several applications, such as data classification, since it overcomes the so-called von Neumann bottleneck. Artificial synapses and neurons can be implemented into conventional hardware using new software, but also be created by diverse spintronic devices and other elements to completely avoid the disadvantages of recent hardware architecture.

neuromorphic computing adaptive computing cognitive computing magnetism micromagnetic simulations magnetic nanoparticles neural network

1. Introduction

Conventional computers have a processing unit and a memory, used to process and to store data, respectively. Other common components are input and output mechanisms, a control unit, and a nonvolatile memory. According to the so-called von Neumann architecture, processing and storage of data are separated ^[1]. This leads to the “von Neumann bottleneck”, meaning that data transport is nowadays slower than data processing and storage ^[2]. While separate buses for data and processing instructions or parallel computing might partly solve this problem, Backus suggested in 1978 to use an alternative program architecture in combination with new rules for state transition ^[3]. For this approach, however, new hardware would be supportive.

One possible solution is based on the idea of neuromorphic computing, also called cognitive or adaptive computing. Brain-inspired computers could work like neuronal networks, be more energy-efficient ^[4], and could learn and solve special mathematical problems faster than recent computers ^[5]. Especially for machine vision, machine hearing, etc., neural network computations for autonomous robots, etc., this approach is often discussed ^[6].

2. Magnetic Tunnel Junctions–Domain Wall Propagation and Different Switching Mechanisms

One of the ideas for data storage devices is based on domain wall motion, driven, e.g., by spin orbit torque in ferromagnet/heavy metal heterostructures ^[7]^[8]. This principle can also be used in neuromorphic computing.

Sengupta et al. suggested an all-spin artificial neural network in which domain wall propagation through ferromagnets was used to emulate neural and synaptic functionalities ^[9]. While common devices are switched between two states ^[10], they suggested a multilayer consisting of a ferromagnet with a domain wall and a heavy metal layer. The latter is necessary to create a spin-orbit torque by applying a charge current, which can control the magnetic domain wall in the ferromagnet ^[11]^[12]^[13]. This system has the advantage of a linear, instead of a step transfer, function, which could be used for complex calculations and especially in neuromorphic computing, where such analogue behavior is often advantageous. Combining it with a pinned ferromagnetic layer on top of the free ferromagnetic layer with the domain wall, a magnetic tunnel junction (MTJ) is formed in which both ferromagnets are separated by a tunnel barrier, typically prepared from MgO or other metal oxides.

It should be mentioned that switching a layer of a magnetic tunnel junction can be done, in general, due to field-induced or current-induced effects, eventually supported by temperature (thermally assisted switching), spin transfer torque, or by the aforementioned spin-orbit torque mechanism.

Using such MTJs, Sengupta et al. proposed a device in which writing is performed by a current flow through the heavy metal underlayer, while the read current flows through the MTJ structure, perpendicular to its tunnel barrier, and is used to measure the conductance which changes typically by several 100% in such a tunnel magnetoresistance (TMR) system ^[14]. In this way, the domain wall position represents the synapse functionality, i.e., the memory—by changing the domain wall position, the “synaptic weight” is modified. This means that the synapse is not switched between two states, as in common computers, but has a nonstep transfer function, enabling storage of several different states. It can also be interpreted as a synapse necessitating more than one current pulse to switch between two states, as is common in the human brain. Computation, on the other hand, is performed by “writing”, i.e., shifting the domain wall position, followed by reading to enable a feedback loop. The validity of this approach was underlined by micromagnetic simulations of the domain wall motion ^[9].

To develop this model further, spiking neurons can be included. The idea of spiking neurons was implemented in the third generation of neural network models, while the first generation was characterized by giving only digital inputs and outputs, and the second generation had a continuous set of output values, corresponding to weighted sums of inputs, as described above and as well-known from analog computations.

Using lateral spin valves, again based on the spin-orbit torque, Sengupta and Roy developed a model in which the MTJ was located at an edge of the free layer. The input spikes were given as current pulses through the heavy metal layer at different time steps, with each input spike moving the domain proportionally to the current value. When the domain wall reached the other edge of the free layer, an output spike was triggered. Interestingly, due to the pinned layer, the domain wall leaks back to its original position when the time distances between input spikes are too large, by this “leaking” even mimicking “forgetting” and not only “learning” ^[15]. Other papers of this group suggest further devices in a full device-circuit-system perspective, using different bio-fidelity from first generation neurons to stochastic spiking neurons ^[16]^[17].

3. Skyrmions

Skyrmions are topologically stable solitons, firstly described by Tony Skyrme in correlation with the atomic nucleus ^[18]. Magnetic skyrmions were found much later ^[19]^[20] and are under examination by diverse research groups since.

Magnetic skyrmions look, at first glance, like magnetic vortex cores, with the magnetization in their core pointing out of plane, i.e., “up” or “down” in a thin magnetic film. The outer edge of the skyrmion consists of spins pointing in the opposite direction. Between middle and outer edge, the magnetic moments are usually tilted along a circle around the middle or canted more and more to the inside or outside, respectively, in this way minimizing the energy of the spins between the extremal positions.

A completely different path was proposed by Pinna et al. They prepared a skyrmion gas, i.e., a diluted irregular skyrmion lattice, and used it to copy a random signal based on skyrmion-skyrmion as well as skyrmion-edge interactions. This small device worked similarly to an integrate-and-fire neuron and could thus be regarded as a neuromorphic computing device ^[21].

Skyrmions were also combined with the idea of reservoir computing, i.e., with the concept of complex artificial neural networks, modeled by recursively connected dynamical systems from self-assembled memristive devices. In such random networks, computation is encoded in the collective dynamic response of the system on an input signal. Prychynenko et al. designed a skyrmion network in a magnetic film and simulated the influence of the anisotropic magneto-resistive effect with or without additional local pinning on the skyrmions in this system ^[22].

4. Magnetic Nanowires and Other Magnetic Nanostructures

Moving magnetic domain walls is not only possible in one of the layers in a magnetic tunnel junction, but also in magnetic nanowires, nanofibers, and other nanostructured magnetic objects. Depending on the interplay between magneto-crystalline and shape anisotropy, sometimes combined with an additional magneto-elastic anisotropy or exchange anisotropy, the path of such a propagating domain wall is defined. Besides, nucleation of one or more domain walls as distinct positions or at different times can be triggered. One typical magnetic element which is often investigated by diverse research groups is the so-called Racetrack memory ^[23]^[24]^[25], which is planned to be used for data storage.

Due to their analog operation mode, such Racetrack memories or similar concepts can be used in neuromorphic computing for data storage and transport. Here, however, it must be taken into account that not only the cross-section, but also a bending radius of magnetic nanowires, significantly influence magnetization reversal and domain wall nucleation ^[26]^[27]^[28] as well as domain wall propagation ^[29]^[30]. Even more challenging is the formation of logic circuits purely from magnetic nanowires ^[31]^[32]^[33].

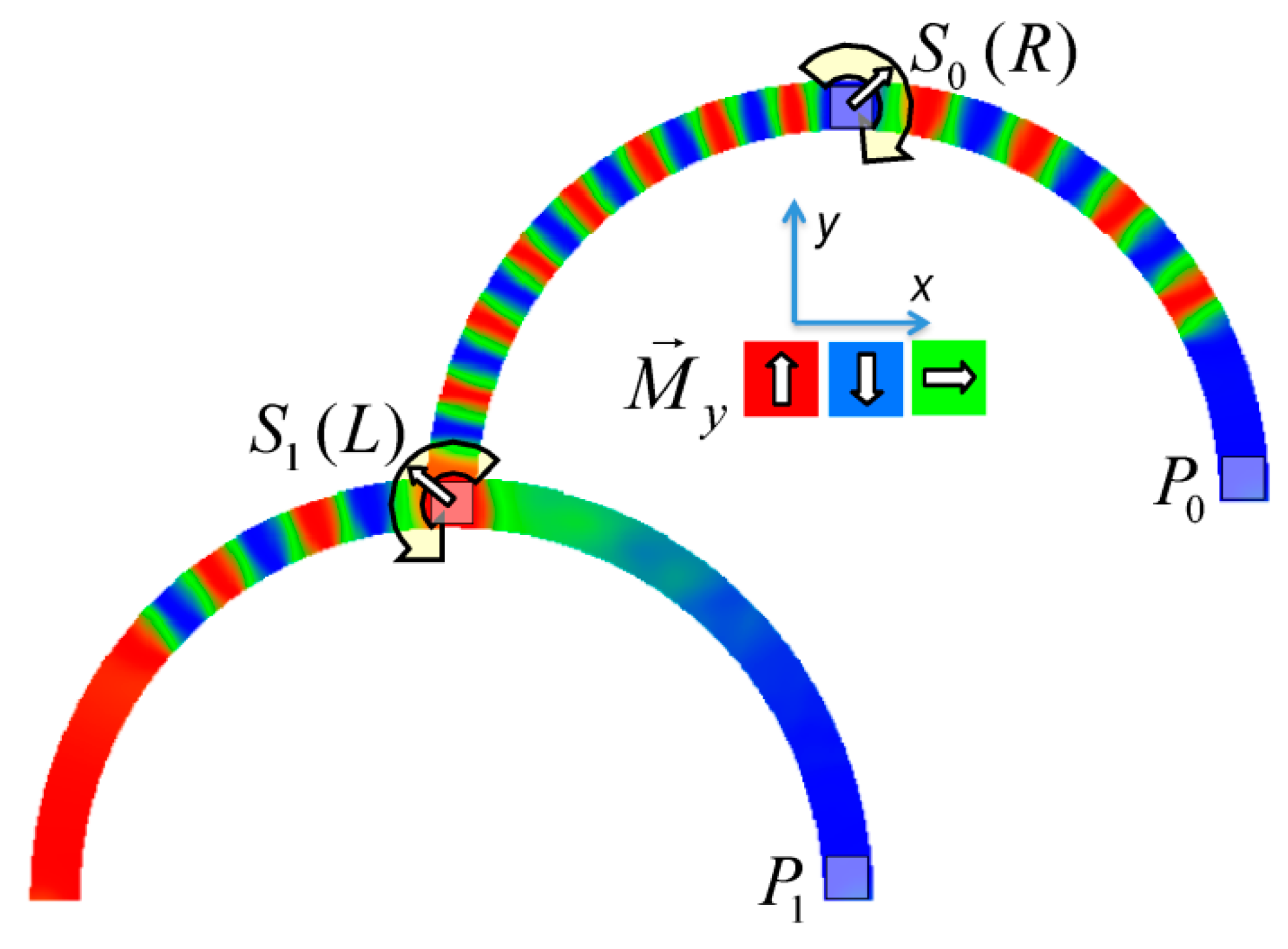
Figure 1 depicts an example of neuro-inspired signal process by a double-curve system, simulated with the Landau-Lifshitzs-Gilbert (LLG) micromagnetic solver Magpar ^[34] for a permalloy sample of rectangular cross-section 10 nm × 60 nm and fiber length 1570 nm. At the positions S0 and S1, two external rotating magnetic fields are applied (1 T, 0.5 GHz). The dimensions of the local-field regions are 50 nm × 50 nm × 10 nm, identical to the sensing regions at P₀ and P₁. The external fields rotate in the x-y plane, either clockwise (R) or counterclockwise (L). Thus, four input combinations of first and second input are possible: LL, LR, RL, and RR, resulting in different output signals, P₀ and P₁. Figure 1 depicts the case of RL.

/media/item_content/202111/61a579c73143dmolecules-25-02550-g007.png

Figure 1. Example of double-curve system with two inputs S_i and two outputs P_i.

5. Memristors and Other Nonmagnetic Neuromorphic Computing Elements

To complete this overview, a short overview of important nonmagnetic neuromorphic elements is given in this section.

The word “memristor” is composed of “memory” and “resistor” and describes, correspondingly, a storage device changing its resistance in dependence on its history, which can be defined as memory. After being described in 1971 ^[35], it was found only in 2007 ^[36]. Opposite to the above-described MTJ with a movable domain wall, the memory of the memristor works chemically, but is also reversible ^[37]. Its advantage is the significantly reduced energy consumption, as compared to recent DRAMs (dynamic random access memories) ^[38]. In addition, this “analog” behavior makes the memristor suitable for neuromorphic computing applications. A large number of publications describes the possible use of memristors as artificial synapses ^[39]^[40]^[41]^[42]^[43] or even neurons ^[44]^[45]^[46]. Alternatively, phase-change materials can be used as synapses ^[47]^[48]^[49]. Finally, photonic materials were also suggested as synapses ^[50]^[51]^[52] or neurons ^[51]^[53]^[54].

References

Neumann, J. First Draft of a Report on the EDVAC. In The Origins of Digital Computers; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 1982; pp. 383–392.
Emma, P.G. Understanding some simple processor-performance limits. IBM J. Res. Dev. 1997, 41, 215–232.
Backus, J. Can programming be liberated from the von Neumann style? A functional style and its algebra of programs. Commun. ACM 1978, 21, 613–641.
Schemmel, J.; Briiderle, D.; Griibl, A.; Hock, M.; Meier, K.; Millner, S. A wafer-scale neuromorphic hardware system for large-scale neural modeling. In Proceedings of the 2010 IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010; pp. 1947–1950.
Schuman, C.; Potok, T.; Patton, R.; Birdwell, J.D.; Dean, M.E.; Rose, G.S.; Plank, J.S. A Survey of Neuromorphic Computing and Neural Networks in Hardware, 2017. Available online: https://www.mdpi.com/1420-3049/21/9/1255/htm (accessed on 18 May 2020).
Burr, J.B. Digital neural network implementations. Neural Netw. Concepts Appl. Implement. 1991, 3, 237–285.
Ryu, K.-S.; Thomas, L.; Yang, S.-H.; Parkin, S. Chiral spin torque at magnetic domain walls. Nat. Nanotechnol. 2013, 8, 527–533.
Bhowmik, D.; Nowakowski, M.E.; You, L.; Lee, O.J.; Keating, D.; Wong, M.; Bokor, J.; Salahuddin, S. Deterministic domain wall mition orthogonal to current flow due to spin orbit torque. Sci. Rep. 2015, 5, 11823.
Sengupta, A.; Shim, Y.; Roy, K. Proposal for an All-Spin Artificial Neural Network: Emulating Neural and Synaptic Functionalities Through Domain Wall Motion in Ferromagnets. IEEE Trans. Biomed. Circuits Syst. 2016, 10, 1152–1160.
Sharad, M.; Fan, D.; Roy, K. Spin-neurons: A possible path to energy-efficient neuromorphic computers. J. Appl. Phys. 2013, 114, 234906.
Emori, S.; Bauer, U.; Ahn, S.-M.; Martínez, E.; Beach, G.S.D. Current-driven dynamics of chiral ferromagnetic domain walls. Nat. Mater. 2013, 12, 611–616.
Ryu, K.-S.; Yang, S.-H.; Thomas, L.; Parkin, S.S.P. Chiral spin torque arising from proximity-induced magnetization. Nat. Commun. 2014, 5, 3910.
Emori, S.; Martínez, E.; Lee, K.-J.; Bauer, U.; Ahn, S.-M.; Agrawal, P.; Bono, D.C.; Beach, G.S.D. Spin Hall torque magnetometry of Dzyaloshinskii domain walls. Phys. Rev. B 2014, 90, 184427.
Hirohata, A.; Sukegawa, H.; Yanagihara, H.; Žutić, I.; Seki, T.; Mizukami, S.; Swaminathan, R. Roadmap for Emerging Materials for Spintronic Device Applications. IEEE Trans. Magn. 2015, 51, 1–11.
Sengupta, A.; Roy, K. Encoding neural and synaptic functionalities in electron spin: A pathway to efficient neuromorphic computing. Appl. Phys. Rev. 2017, 4, 041105.
Sengupta, A.; Roy, K. A Vision for All-Spin Neural Networks: A Device to System Perspective. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 2267–2277.
Sengupta, A.; Han, B.; Roy, K. Toward a spintronic deep learning spiking neural processor. In Proceedings of the 2016 IEEE Biomedical Circuits and Systems Conference (BioCAS), Shanghai, China, 17–19 October 2016; pp. 544–547.
Skyrme, T. A unified field theory of mesons and baryons. Nucl. Phys. 1962, 31, 556–569.
Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Boni, P. Skyrmion Lattice in a Chiral Magnet. Science 2009, 323, 915–919.
Jonietz, F.; Mühlbauer, S.; Pfleiderer, C.; Neubauer, A.; Münzer, W.; Bauer, A.; Adams, T.; Georgii, R.; Böni, P.; Duine, R.A.; et al. Spin Transfer Torques in MnSi at Ultra-low Current Densities. Science 2010, 330, 1648–1651.
Pinna, D.; Araujo, F.A.; Kim, J.-V.; Cros, V.; Querlioz, D.; Bessiere, P.; Droulez, J.; Grollier, J. Skyrmion Gas Manipulation for Probabilistic Computing. Phys. Rev. Appl. 2018, 9, 064018.
Prychynenko, D.; Sitte, M.; Litzius, K.; Krueger, B.; Burianoff, G.; Kläui, M.; Sinova, J.; Everschor-Sitte, K. Magnetic Skyrmion as a Nonlinear Resistive Element: A Potential Building Block for Reservoir Computing. Phys. Rev. Appl. 2018, 9, 14034.
Kumar, D.; Jin, T.; Al Risi, S.; Sbiaa, R.; Lew, W.S.; Piramanayagam, S.N. Domain Wall Motion Control for Racetrack Memory Applications. IEEE Trans. Magn. 2018, 55, 1–8.
Tanaka, Y.; Hirai, T.; Koyama, T.; Chiba, D. Electric-field-induced magnetic domain writing in a Co wire. Appl. Phys. Express 2018, 11, 053005.
Dutta, S.; Siddiqui, S.A.; Currivan-Incorvia, J.A.; Ross, C.A.; Baldo, M.A. The Spatial Resolution Limit for an Individual Domain Wall in Magnetic Nanowires. Nano Lett. 2017, 17, 5869–5874.
Blachowicz, T.; Ehrmann, A. Magnetization reversal in bent nanofibers of different cross sections. J. Appl. Phys. 2018, 124, 152112.
Blachowicz, T.; Kosmalska, D.; Döpke, C.; Leiste, H.; Hahn, L.; Ehrmann, A. Varying steps in hysteresis loops of Co square nano-frames. J. Magn. Magn. Mater. 2019, 491, 165619.
Kern, P.; Döpke, C.; Blachowicz, T.; Steblinski, P.; Ehrmann, A. Magnetization reversal in ferromagnetic Fibonacci nano-spirals. J. Magn. Magn. Mater. 2019, 484, 37–41.
Kunz, A. Field induced domain wall collisions in thin magnetic nanowires. Appl. Phys. Lett. 2009, 94, 132502.
Moreno, R.; Carvalho-Santos, V.L.; Espejo, A.P.; Laroze, D.; Chubykalo-Fesenko, O.; Altbir, D. Oscillatory behavior of the domain wall dynamics in a curved cylindrical magnetic nanowire. Phys. Rev. B 2017, 96, 184401.
Kim, S.-K.; Park, H.-K.; Yang, J.; Kim, J.; Yoo, M.-W. Spin-wave duplexer studied by finite-element micromagnetic simulation. Sci. Rep. 2018, 8, 16511.
Wang, Q.; Brächer, T.; Mohseni, M.; Hillebrands, B.; Vasyuchka, V.I.; Chumak, A.V.; Pirro, P. Nanoscale spin-wave wake-up receiver. Appl. Phys. Lett. 2019, 115, 092401.
Garg, C.; Pushp, A.; Yang, S.-H.; Phung, T.; Hughes, B.P.; Rettner, C.; Parkin, S.S.P. Highly Asymmetric Chiral Domain-Wall Velocities in Y-Shaped Junctions. Nano Lett. 2018, 18, 1826–1830.
Scholz, W.; Fidler, J.; Schrefl, T.; Suess, D.; Dittrich, R.; Forster, H.; Tsiantos, V. Scalable parallel micromagnetic solvers for magnetic nanostructures. Comput. Mater. Sci. 2003, 28, 366–383.
Chua, L.O. Memristor–the missing circuit element. IEEE Trans. Circuit Theor. 1971, 18, 507–519.
Wang, Q.; Shang, D.-S.; Wu, Z.; Chen, L.; Li, X. “Positive” and “negative” electric-pulse-induced reversible resistance switching effect in Pr0.7Ca0.3MnO3 films. Appl. Phys. A 2006, 86, 357–360.
Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83.
Gutmann, E. Maintaining Moore’s Law with New Memristor Circuits. Ars Technica 2008. Available online: https://arstechnica.com/uncategorized/2008/05/maintaining-moores-law-with-new-memristor-circuits (accessed on 4 April 2020).
Zayer, F.; Dghais, W.; Belgacem, H.; Fakhreddine, Z. Modeling framework and comparison of memristive devices and associated STDP learning windows for neuromorphic applications. J. Phys. D Appl. Phys. 2019, 52, 393002.
Dang, B.; Wu, Q.; Sun, J.; Zhao, M.; Wang, S.; Song, F.; Yang, M.; Ma, X.; Wang, H.; Hao, Y. Physically Transient Memristor Synapse Based on Embedding Magnesium Nanolayer in Oxide for Security Neuromorphic Electronics. IEEE Electron Device Lett. 2019, 40, 1265–1268.
Pan, X.; Shuai, Y.; Wu, C.; Zhang, L.; Guo, H.; Cheng, H.; Peng, Y.; Qiao, S.; Luo, W.; Wang, T.; et al. Ar+ ions irradiation induced memristive behavior and neuromorphic computing in monolithic LiNbO3 thin films. Appl. Surf. Sci. 2019, 484, 751–758.
Wang, Y.; Zhang, Z.; Xu, M.; Yang, Y.; Ma, M.; Li, H.; Pei, J.; Shi, L. Self-Doping Memristors with Equivalently Synaptic Ion Dynamics for Neuromorphic Computing. ACS Appl. Mater. Interfaces 2019, 11, 24230–24240.
Nagata, Z.; Shimizu, T.; Isaka, T.; Tohei, T.; Ikarashi, N.; Sakai, A. Author Correction: Gate Tuning of Synaptic Functions Based on Oxygen Vacancy Distribution Control in Four-Terminal TiO2-x Memristive Devices. Sci. Rep. 2019, 9, 15166.
An, H.; Ehsan, M.A.; Zhou, Z.; Shen, F.; Yi, Y. Monolithic 3D neuromorphic computing system with hybrid CMOS and memristor-based synapses and neurons. Integration 2019, 65, 273–281.
Bao, L.; Kang, J.; Fang, Y.; Yu, Z.; Wang, Z.; Yang, Y.; Cai, Y.; Huang, R. Artificial Shape Perception Retina Network Based on Tunable Memristive Neurons. Sci. Rep. 2018, 8, 13727.
Irmanova, A.; James, A.P. Neuron inspired data encoding memristive multi-level memory cell. Analog. Integr. Circuits Signal Process. 2018, 95, 429–434.
Chakraborty, I.; Saha, G.; Roy, K. Photonic In-Memory Computing Primitive for Spiking Neural Networks Using Phase-Change Materials. Phys. Rev. Appl. 2019, 11, 014063.
Nandakumar, S.R.; Le Gallo, M.; Boybat, I.; Rajendran, B.; Sebastian, A.; Eleftheriou, E. A phase-change memory model for neuromorphic computing. J. Appl. Phys. 2018, 124, 152135.
Ambrogio, S.; Ciocchini, N.; Laudato, M.; Milo, V.; Pirovano, A.; Fantini, P.; Ielmini, D. Unsupervised Learning by Spike Timing Dependent Plasticity in Phase Change Memory (PCM) Synapses. Front. Mol. Neurosci. 2016, 10, 384012.
Sun, Y.; Qian, L.; Xie, D.; Lin, Y.; Sun, M.; Li, W.; Ding, L.; Ren, T.; Palacios, T. Photoelectric Synaptic Plasticity Realized by 2D Perovskite. Adv. Funct. Mater. 2019, 29.
Feldmann, J.; Youngblood, N.; Wright, C.D.; Bhaskaran, H.; Pernice, W. All-optical spiking neurosynaptic networks with self-learning capabilities. Nature 2019, 569, 208–214.
Kumar, M.; Abbas, S.; Kim, J. All-Oxide-Based Highly Transparent Photonic Synapse for Neuromorphic Computing. ACS Appl. Mater. Interfaces 2018, 10, 34370–34376.
Robertson, J.; Wade, E.; Hurtado, A. Electrically Controlled Neuron-Like Spiking Regimes in Vertical-Cavity Surface-Emitting Lasers at Ultrafast Rates. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1–7.
Chakraborty, I.; Saha, G.; Sengupta, A.; Roy, K. Toward Fast Neural Computing using All-Photonic Phase Change Spiking Neurons. Sci. Rep. 2018, 8, 12980.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Biochemical Research Methods

Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Tomasz BLACHOWICZ

Andrea Ehrmann

View Times: 539

Update Date: 01 Dec 2021

Table of Contents

Video Upload Options

Confirm