| Version | Summary | Created by | Modification | Content Size | Created at | Operation |
|---|---|---|---|---|---|---|
| 1 | Bibi Aamirah Shafaa Emambocus | + 1381 word(s) | 1381 | 2021-11-15 10:38:40 | | | |
| 2 | Amina Yu | -22 word(s) | 1359 | 2021-11-25 04:00:12 | | |
Video Upload Options
Optimization algorithms are essential for numerous optimization applications where usually certain parameters are minimized or maximized by considering an objective function. These algorithms include exact methods and heuristic algorithms such as swarm intelligence algorithms. Swarm intelligence is a discipline which makes use of a number of agents, thereby forming a population in which individuals interact among themselves and with their environment, to give rise to a global intelligent behavior. The Dragonfly Algorithm (DA) is a swarm intelligence algorithm that was proposed in 2016, and it is inspired by the behavior of dragonflies in nature. It has been found to have a higher performance than some of the most popular evolutionary algorithms, such as the genetic algorithm (GA), and swarm intelligence algorithms such as particle swarm optimization (PSO). Owing to its high effectiveness and efficiency, it has been utilized in multifarious applications and attempts to further improve its performance have been made and hence a number of hybrids of DA have been proposed.
1. Introduction
Optimization algorithms are essential for numerous optimization applications where usually certain parameters are minimized or maximized by considering an objective function. Optimization algorithms can be classified as either deterministic or non-deterministic [1]. Deterministic algorithms are exact methods, and usually they need a substantial amount of time and resources for solving large optimization problems. Hence, non-deterministic algorithms, also called heuristic algorithms, are being increasingly used and developed. They can be based on various natural processes; for example, trajectory-based, physics-based or population-based, which can be either nature- or bio-inspired [1]. Swarm intelligence algorithms are classified as nature-inspired population-based heuristic optimization algorithms.
Swarm intelligence is a discipline which is utilized for solving optimization problems by producing low cost, fast and robust solutions. Its technique consists of making use of a number of agents, thereby forming a population in which individuals interact among themselves and with their environment, to give rise to a global intelligent behavior. There exist numerous swarm intelligence algorithms, such as ant colony optimization (ACO), grey wolf optimization (GWO), firefly algorithm (FA), whale optimization algorithm (WOA), bee colony optimization (BCO), and particle swarm optimization (PSO).
The Dragonfly Algorithm (DA) is a swarm intelligence algorithm that was proposed in 2016 [2], and it is inspired by the behavior of dragonflies in nature. It has been found to have a higher performance than some of the most popular evolutionary algorithms, such as the genetic algorithm (GA), and swarm intelligence algorithms such as particle swarm optimization (PSO). Owing to its high effectiveness and efficiency, it has been utilized in multifarious applications and attempts to further improve its performance have been made and hence a number of hybrids of DA have been proposed. Our motivation for working on this algorithm is that DA and its hybrids have proven to be useful in multifarious applications and they also have a higher performance as compared to other swarm intelligence algorithms and their hybrids.
Table 1 shows a comparison between our survey and the previous surveys on DA in terms of the contents presented in the surveys.
| Our Survey | [3] | [4] | [5] | [6] | |
|---|---|---|---|---|---|
| Background on DA | ✓ | ✓ | ✓ | ✓ | ✓ |
| Applications of DA based on domain | ✓ | ✓ | ✓ | ✓ | ✓ |
| Analysis of the performance of DA as compared to other swarm intelligence algorithms | ✓ | ✓ | ✓ | ✓ | |
| Consideration of the limitations of DA and proposed future directions | ✓ | ✓ | ✓ | ✓ | ✓ |
| Analysis of the performance of the hybrids of DA as compared to original DA | ✓ | ✓ | ✓ | ✓ | ✓ |
| Consideration of the methods employed to enhance the original DA obtaining the hybrids | ✓ | ✓ | ✓ | ✓ | ✓ |
| Analysis of the limitations of the hybrids of DA | ✓ | ||||
| Categorization of hybrids according to the type of problem | ✓ | ||||
| Taxonomies to categorize the hybrids of DA according to the performance improvement (effectiveness, efficiency) | ✓ | ||||
| Taxonomies of hybrids of DA according to effectiveness improving method | ✓ |
2. Dragonfly Algorithm
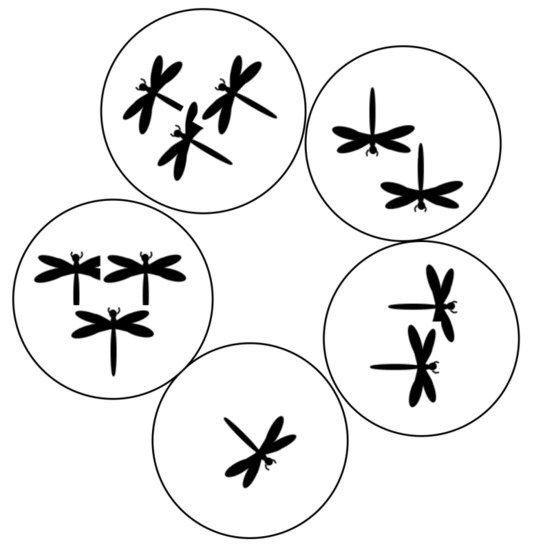
The inspiration for the dragonfly algorithm is derived from the static and dynamic swarming behaviours of dragonflies in nature. The static and dynamic swarming behaviors are representative of the two requisite phases of optimization: exploration and exploitation. In a static swarm, as in Figure 1 , dragonflies create sub-swarms and fly over different regions. This is tantamount to exploration, and it helps the algorithm to locate good areas of the search space. Conversely, in a dynamic swarm, as in Figure 2 , dragonflies fly in a bigger swarm and along the same direction. This type of swarming is equivalent to the exploitation of an algorithm, which helps it to converge to the global optimum.
Five factors are used for to direct the dragonflies in the exploration and exploitation phases; namely, separation, alignment, cohesion, food factor and enemy factor. The separation weight (s), alignment weight (a), cohesion weight (c), food factor (f), enemy factor (e) and the inertia weight (w) are used for controlling the factors. The goal is to ensure that the swarm survives by attracting it towards food sources and distracting it away from enemies. The best solution found in an iteration is selected as the food source and the worst solution found is selected as the enemy. The weights of the factors are adjusted so as to have high alignment and low cohesion in the exploration phase and low alignment and high cohesion in the exploitation phase. The weights are changed accordingly to allow the transition of the algorithm from the exploration to the exploitation phase.
The step vector and position vectors of each dragonfly are updated in every iteration until the end criterion is met. The pseudocode of the dragonfly algorithm is given in Algorithm 1.
3. Hybrids of DA
This section discuss the hybrids of the dragonfly algorithm which have been applied for solving continuous and single-objective problems, and hence there exists the continuous version of the algorithm. Some of these algorithms have also been used for binary or multi-objective problems, and therefore the binary and single-objective or the continuous and multi-objective versions of these algorithms have also been proposed in addition to the continuous and single-objective one.
In [7], a hybrid modified DA and whale optimization is proposed to optimally schedule microgrid with islanding constraints to achieve the best quality. Since this is a multi-objective problem where the parameters can have any real value within a specified range, the continuous and multi-objective version of the algorithm is proposed and used.
In [8], a hybrid DA-DE, called IEDA, is proposed for the optimal design of a hybrid power active filter. Since this is a multi-objective problem where the parameters can have any real value within a specified range, the continuous and multi-objective version of the algorithm is proposed and used.
There is a hybrid algorithm on which we are working, and it also improves the effectiveness of DA by improving its exploitation phase. The algorithm [9] makes use of hill climbing algorithm as a local search. In each iteration, the position obtained by DA is further updated by hill climbing in order to obtain better positions.
4. Applications of DA and Hybrids
The multi-objective version of DA, MODA has been applied to wind-solar-hydro power scheduling in [10] to provide an optimal scheduling model and to multi-objective optimal power flow problem in [11] for minimizing total fuel cost, real power loss, total emission, and voltage deviation.
The hybrid DA-PSO [12] has been used for the multiobjective optimal power flow problem to optimize selected objective functions, while satisfying a set of equality and inequality constraints and the hybrid DA-GA [13] has been applied to optimal power flow problem to compute the locational marginal prices (LMP) for improved reliability.
DA and its hybrids have also been applied for optimal resource allocation. In [14], DA is used for the optimal resource allocation in cloud computing by optimizing parameters like load balance, execution time and response time for optimal allocation of resources to tasks and to establish load balance. In [15], it has been used to optimally allocate generators and capacitors in a distribution system, and in [16], it has been used for the distributed generation (DG) placement in distributed networks to obtain the optimal DG units size and placement.
Apart from the applications mentioned in the previous sections, DA has been applied to the vehicle routing problem with time window constraints (VRPTW) in [17] to find an optimized route and to the open loop nonlinear dynamic systems control in [18] to find the optimal parameters.
References
- Knypinski, Ł. Constrained optimization of line-start PM motor based on the gray wolf optimizer. Eksploat. Niezawodn.-Maint. Reliab. 2021, 23, 10.
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073.
- Meraihi, Y.; Ramdane-Cherif, A.; Acheli, D.; Mahseur, M. Dragonfly algorithm: A comprehensive review and applications. Neural Comput. Appl. 2020, 32, 16625–16646.
- Rahman, C.M.; Rashid, T. A Survey on Dragonfly Algorithm and its Applications in Engineering. arXiv 2020, arXiv:2002.12126.
- Rahman, C.M.; Rashid, T.A. Dragonfly Algorithm and Its Applications in Applied Science Survey. Comput. Intell. Neurosci. 2019, 2019, 9293617.
- Alshinwan, M.; Abualigah, L.; Shehab, M.; Elaziz, M.A.; Khasawneh, A.M.; Alabool, H.; Hamad, H.A. Dragonfly algorithm: A comprehensive survey of its results, variants, and applications. Multimed. Tools Appl. 2021, 80, 14979–15016.
- Kumari, K.K.; Babu, R.S.R. An efficient modified dragonfly algorithm and whale optimization approach for optimal scheduling of microgrid with islanding constraints. Trans. Inst. Meas. Control. 2021, 43, 421–433.
- Dai, W.; Li, C.; Cui, Z.; Wu, Y.; Zhang, L.; Huang, J. An Improved Dragonfly Algorithm With Higher Exploitation Capability to Optimize the Design of Hybrid Power Active In Proceedings of the Filter. IEEE Access 2020, 8, 155020–155038.
- Emambocus, B.A.S.; Jasser, M.B. Towards An Optimized Dragonfly Algorithm Using Hill Climbing Local Search To Tackle The Low Exploitation Problem. In Proceedings of the 2021 International Conference on Software Engineering Computer Systems and 4th International Conference on Computational Science and Information Management (ICSECS-ICOCSIM), Pekan, Malaysia, 24–26 August 2021; pp. 306–311.
- Li, J.; Lu, J.; Yao, L.; Cheng, L.; Qin, H. Wind-Solar-Hydro power optimal scheduling model based on multi-objective dragonfly algorithm. Energy Procedia 2019, 158, 6217–6224.
- Ouafa, H.; Linda, S.; Tarek, B. Multi-Objective Optimal Power Flow Considering the Fuel Cost, Emission, Voltage Deviation and Power Losses Using Multi-Objective Dragonfly Algorithm. In Proceedings of the 2017 International Conference on Recent Advances in Electrical Systems, Hammamet, Tunisia, 22–24 December 2017; p. 8.
- Khunkitti, S.; Siritaratiwat, A.; Premrudeepreechacharn, S.; Chatthaworn, R.; Watson, N. A Hybrid DA-PSO Optimization Algorithm for Multiobjective Optimal Power Flow Problems. Energies 2018, 11, 2270.
- Veeramsetty, V.; Venkaiah, C.; Kumar, D.M.V. Hybrid genetic dragonfly algorithm based optimal power flow for computing LMP at DG buses for reliability improvement. Energy Syst. 2018, 9, 709–757.
- Amini, Z.; Maeen, M.; Jahangir, M.R. Providing a load balancing method based on dragonfly optimization algorithm for resource allocation in cloud computing. Int. J. Networked Distrib. Comput. 2018, 6, 8.
- Sudabattula, S.K.; M, K.; Velamuri, S.; Melimi, R.K. Optimal Allocation of Renewable Distributed Generators and Capacitors in Distribution System Using Dragonfly Algorithm. In Proceedings of the 2018 International Conference on Intelligent Circuits and Systems (ICICS), Phagwara, India, 19–20 April 2018; pp. 393–396.
- Suresh, M.C.V.; Belwin, E.J. Optimal DG placement for benefit maximization in distribution networks by using Dragonfly algorithm. Renewables Wind. Water, Sol. 2018, 5, 4.
- Liu, C.; Tao, W.; Zhao, C.; Li, X.; Su, Y.; Sun, Z. Research on Vehicle Routing Problem with time Windows Based on the Dragonfly Algorithm. In Proceedings of the 2019 IEEE Intl Conf on Dependable, Autonomic and Secure Computing, Intl Conf on Pervasive Intelligence and Computing, Intl Conf on Cloud and Big Data Computing, Intl Conf on Cyber Science and Technology Congress (DASC/PiCom/CBDCom/CyberSciTech), Fukuoka, Japan, 5–8 August 2019; pp. 142–148.
- Panteleev, A.; Stanovskaya, Y. The Dragonfly Algorithm for Parametric Optimization of Open Loop Nonlinear Dynamic Systems Control. In Proceedings of the Computational Mechanics and Modern Applied Software Systems (CMMASS’2019), Crimea, Russia, 24–31 May 2019; p. 020027.