Compression of Neural Networks

Version	Summary	Created by	Modification	Content Size	Created at	Operation
1		Freddy Gabbay	+ 2108 word(s)	2108	2021-10-28 08:40:03	\|
2	Done	Jason Zhu	Meta information modification	2108	2021-11-08 06:48:06	\| \|
3	Done	Jason Zhu	Meta information modification	2108	2021-11-08 06:49:52	\| \|
4	Done	Jason Zhu	Meta information modification	2108	2021-11-08 06:51:00	\|

This entry is adapted from the peer-reviewed paper 10.3390/math9202612

Researchers propose the value-locality-based compression (VELCRO) algorithm for neural networks. VELCRO is a method to compress general-purpose neural networks that are deployed for a small subset of focused specialized tasks.

VELCRO Algorithm Compression Algorithm

1. Introduction

Convolutional Neural Networks (CNNs) are broadly employed by numerous computer vision applications such as autonomous systems, healthcare, retail, and security. Over time, the processing requirements and complexity of CNN models have significantly increased. For example, AlexNet ^[1], which was introduced in 2012, has eight layers, whereas ResNet-101 ^[2], which was released in 2015, uses 101 layers and requires an approximately sevenfold-greater computational throughput ^[3]. The increasing model complexity in conjunction with large datasets used for model training has endowed CNNs with phenomenal performance for various computer vision tasks ^[4]. Typically, large complex networks can further extend their capacity to learn complex image features and properties. The growing model size of CNNs and the requirement of significant processing power have become major deployment challenges for migrating CNN models into mobile, Internet of Things, and edge applications. Such applications incur limited computational and memory resources, energy constraints, and system cost and, in many cases, cannot rely on cloud computational resources due to privacy, online communication network availability, and real-time considerations.

The compression of CNN models without excessive performance loss significantly facilitates their deployment by a variety of edge systems. Such compression has the potential to reduce computational requirements, save energy, reduce memory bandwidth and storage requirements, and shorten inference time. Various techniques have been suggested to compress CNN models, one of the most common of which is pruning ^[5]^[6]^[7], which exploits the tendency to over-parameterize CNNs ^[8]. Pruning trades off degradation in model prediction accuracy for model size by removing weights, Output Feature Maps (OFMs), or filters that make minor or no contribution to the inference of a network. Quantization ^[9]^[10]^[11]^[12] is another common technique that attempts to further compress network size by reducing the number of bits used to represent weights, filters, and OFMs with only a minor impact on accuracy.

There is the value-locality-based compression (VELCRO) algorithm. VELCRO is a method to compress deep neural networks that were originally trained for a large set of diverse classification tasks but are deployed for a smaller subset of specialized tasks. Although this work focuses on CNN models, VELCRO can be used to compress any deep neural network. The main principle of VELCRO is based on the property of value locality, which is introduced herein in the context of neural networks. This property suggests that, when the network is used for specialized tasks, a proximal range of values are produced by the activation functions in the inference process. VELCRO consists of two stages: a preprocessing stage, which identifies activation-function output elements with a high degree of value locality, and a compression stage, which replaces these activation elements with their corresponding arithmetic averages. As a result, VELCRO avoids not only the computation of these activation elements but also the convolution computation of their corresponding OFM elements. VELCRO also requires significantly fewer computational resources than common pruning techniques due to the avoidance of back propagation training.

2. VELCRO

The VELCRO compression algorithm relies on the fundamental property of value locality.

2.1. Value Locality of Specialized Convolutional Neural Networks

The principle of the method proposed to compress specialized CNNs is based on the property of value locality. Value locality suggests that, when a CNN model runs specialized tasks, the output values of the activation tensor is in proximity through inference of images. The rationale behind this theory relies on the assumption that the inferred images, which already have a certain level of similarity, exhibit common features such as patterns, textures, shapes, and concepts. As a result, the intermediate layers of the model produce similar values in the vicinity. Figure 1 explains the property of value locality by illustrating the activation-function output tensors in each convolution layer k and channel c. In this example, the set of elements A^(m)[k][c][i][j] for images m = 0, 1, …, N − 1 in the activation tensor is populated with values in proximity through the inference between images.

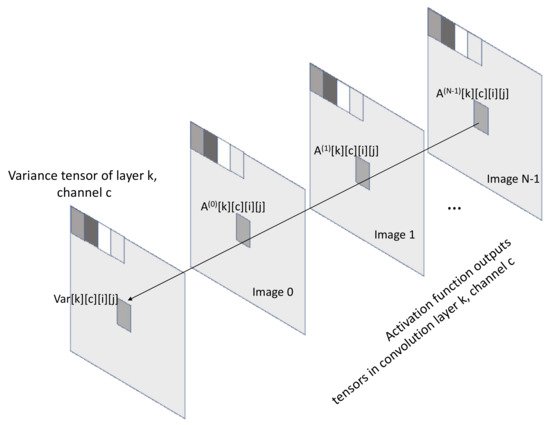
Figure 1. Value locality: The elements with coordinates i, j of the activation-function output tensor in convolutional layer k, channel c, are populated with values in proximity through the inference between images 0 to N − 1. The variance tensor V serves to measure the degree of value locality.

For every convolution layer k, we define a variance tensor V[k], where each element V[k][c][i][j] in the variance tensor is defined as

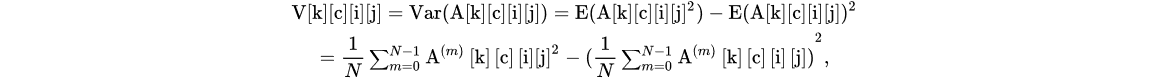
where c is the channel index and i and j are the element coordinates.

Variance tensor is used as a measure to quantify the proximity of values for every activation tensor element A[k][c][i][j]. Thereby, a small value of V[k][c][i][j] suggests that the corresponding activation element has a high degree of value locality. The proposed compression algorithm leverages such activation elements for compression.

2.2. VELCRO Algorithm for Specialized Neural Networks

The VELCRO algorithm consists of two stages: preprocessing and compression.

Preprocessing stage: In this stage, VELCRO makes an inference by applying the original CNN model to a small subset of images from the specialized task preprocessing dataset. Note that the performance of the compressed model is evaluated on a validation dataset which is distinct from the preprocessing dataset. During this stage, the variance tensor is calculated by using Equation (1) for each activation output in each convolution layer in the CNN model. Because the preprocessing stage of VELCRO relies only on inference, it involves a significantly smaller computational overhead with respect to traditional compression methods, which employ heavy backpropagation training processes that can last from a few hours up to hundreds of hours ^[13].

Compression stage: The compression stage uses a tuple of threshold values provided by the user as a hyperparameter for the algorithm. Each threshold element in the tuple corresponds to an individual activation function in each convolution layer. The threshold value of each layer represents the percentile of elements in the variance tensor to be compressed by the algorithm. All elements in the activation tensor with a variance within the percentile threshold are replaced by the arithmetic average constant of the elements located in the same corresponding coordinates. All other activation elements remain unchanged. Replacing activation function output elements by constants avoids not only the activation function computation but also the particular convolution computation of their related OFM elements. In fact, the compression savings of each layer is determined by the corresponding threshold, so the user can determine the overall compression-saving ratio C for the model through the threshold tuple as follows:

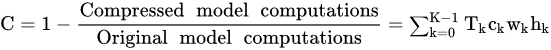
where the tuple T = {T₀, T₁, …, T_K} contains the threshold values for the activation in each convolution layer. In addition, c_k, w_k, and h_k are the number of channels, the width, and the height of the activation function output tensor for convolution layer k, respectively.

3. Performance of Compression Algorithm

Researchers examine the compression-saving ratio of the VELCRO algorithm on three groups of specialized tasks: cats, cars, and dogs. Only a very small subset (<2%) of images from the preprocessing dataset has been used for the preprocessing stage of the algorithm, while the remaining images have used for the validation of the compressed model. This approach is essential in order to perform an unbiased evaluation of the model performance and preserved the generalization property of the model. Figure 2a–c present the top-1 prediction accuracy versus the compression-saving ratio for cars, dogs, and cats, respectively. The experimental analysis is applied to the ResNet-18, GoogLeNet, and MobileNet V2 CNN models. For each compression-saving ratio, we examine different thresholds by running trial-and-error and choose those that produce the highest top-1 accuracy. Table 1 summarizes the maximum compression-saving ratio for each group of specialized tasks and each CNN model that produces the same accuracy as the original uncompressed model.

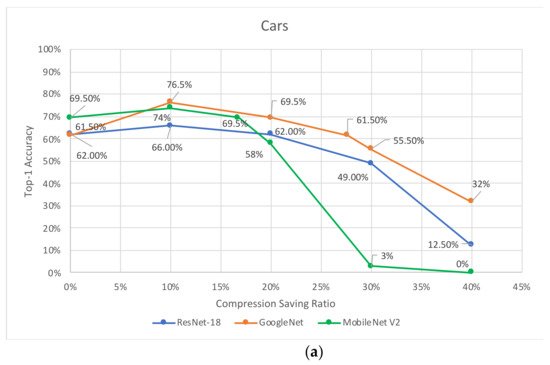
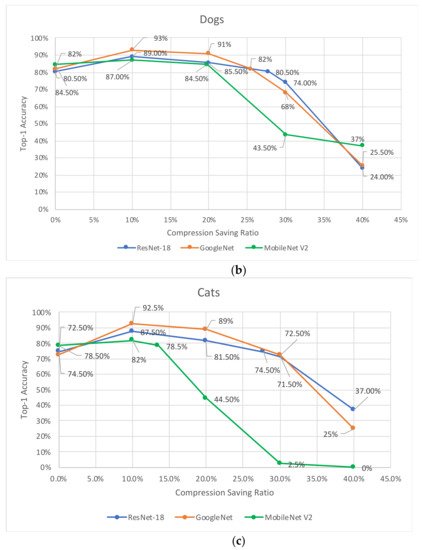
Figure 2. Accuracy for ResNet-18, GoogLeNet, and MobileNet V2 versus compression-saving ratio for specialized tasks: (a) Cars, (b) Dogs, and (c) Cats.

Table 1. Maximum compression-saving ratio achieved while maintaining the accuracy of the original uncompressed CNN model.

Specialized Task	ResNet-18	GoogLeNet	MobileNet V2
Cats	27.73%	30.00%	13.50%
Dogs	27.70%	25.46%	19.76%
Cars	20.00%	27.70%	16.80%

The experimental results indicate that VELCRO produces a compression-saving ratio of 20.00–27.73% in ResNet-18 and 25.46–30.00% in GoogLeNet. The higher compression-saving ratio in GoogLeNet is attributed to the fact that GoogLeNet uses significantly a greater number of parameters and thereby has higher potential to leverage value locality. This explains why GoogLeNet better leverages value locality when the network is employed for special tasks. Conversely, MobileNet V2 produces a smaller compression-saving ratio, 13.50–19.76%, for the specialized tasks examined. These results comply with our previous measurements of the distribution of the variance tensor elements, which imply that the potential of leveraging value locality in MobileNet V2 is smaller than that of the other CNNs examined. This is explained by the fact that MobileNet V2 is much more compact than the other CNNs examined and thereby has a lower potential to leverage value locality.

Note that VELCRO does not aim to compress the network memory footprint but rather to reduce the computational requirements. Therefore, any comparison of VELCRO to pruning approaches should consider computation aspects rather than the number of parameters in the network. Table 2 compares the VELCRO algorithm with other pruning approaches for both specialized CNNs and general-purpose ones. Although VELCRO achieves smaller computation savings, it requires significantly fewer computational resources than common pruning techniques ^[13] due to the avoidance of back propagation training.

Table 2. Comparison summary of VELCRO with respect to punning techniques. We also examine the output of the activation functions compressed by VELCRO.

Compression Method	Network	Specialized Task	Training Required	Computation Acceleration	Accuracy Loss
Taylor criterion ^[14]	AlexNet	Yes	Yes	1.9X	0.3%
CURL ^[15]	MobileNet V2 ResNet-50	Yes Yes	Yes Yes	3X 4X	Up to 4% Up to 2%
Deep compression ^[16]	Various CNN models	No	Yes	3X	None
Weights and connection learning ^[17]	AlexNet	No	Yes	3X	None
KSE ^[18]	ResNet-50	No	Yes	3.8–4.7X	0.84–0.64%
VELCRO	ResNet-18 GoogLeNet MobileNet V2	Yes	No	1.25–1.38X 1.38–1.42X 1.15–1.24X	None None None

Table 3 presents the percent compression of activation elements with zero value out of all the compressed activation elements. The results in Table 2 correspond to the compression-saving ratios in Table 1 (i.e., when the network achieves maximum compression without losing accuracy). With ResNet-18 and GoogLeNet, the fraction of compressed zero values is in the range 0.08–0.31% and 0.56–0.64%, respectively. In contrast, MobileNet V2 produces a significantly larger fraction of compressed zero values: 10.48–14.91%, which is attributed to the fact that MobileNet V2 is a much more compact model than the other CNNs. These results indicate that VELCRO offers an extended level of compression with respect to pruning, which aims to remove weak connections of zero values.

Table 3. Compressed activation elements with zero value as a percent of all compressed activation elements.

Specialized Task	ResNet-18	GoogLeNet	MobileNet V2
Cats	0.08%	0.56%	14.91%
Dogs	0.20%	0.63%	10.48%
Cars	0.31%	0.64%	12.00%

Another important result gained from Figure 9a–c is that, when VELCRO is used with a relatively moderate compression ratio, it produces a significant increase in accuracy. The results are presented in Table 4, which summarizes the maximum top-1 accuracy achieved by VELCRO. These results are attributed to the fact that a relatively moderate level of compression helps the network leverage value locality to strengthen connections, thereby increasing the probability of favoring the prediction of classes that are in the scope of the specialized tasks.

Table 4. The maximum top-1 accuracy increase produced by VELCRO with respect to the uncompressed model when used for specialized tasks.

Specialized Task	ResNet-18	GoogLeNet	MobileNet V2
Cats	13.00%	20.00%	3.50%
Dogs	8.50%	11.00%	2.50%
Cars	4.00%	15.00%	4.50%

5. Hardware Implementation

Researchers demonstrate the computational optimization and energy savings of VELCRO through hardware implementation on the Xilinx^® Alveo™ U280 Data Center accelerator card ^[19]. Our hardware implementation, which is illustrated in Figure 3, consists of 16 instance modules where each is comprised of a two-dimensional convolution layer with a 64 × 64 input feature map (IFMAP), 3 × 3 filter, and a ReLU activation function. In addition, each module also includes a compression control logic which skips the compressed computations and replaces them with their corresponding arithmetic averages.

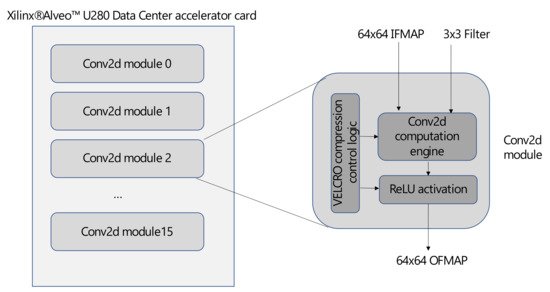
Figure 3. VELCRO compression implementation on Xilinx^® Alveo^TM U280 Accelerator Card.

Figure 4 presents the (normalized) throughput and energy consumption of a single module instance, denoted as conv2d, which consists of the hardware implementation of a two-dimensional convolution layer and ReLU activation. As expected, the computational throughput of the conv2d layer, which is measured as the number of conv2d operations per second, exhibits a growth rate proportional to

\frac{1}{1 - C}

1/(1-C),where C is the compression saving ratio). In addition, it can be observed that the energy consumption related to the computation of a single conv2d layer decays linearly with the compression saving ratio. Thereby, for the compression saving results presented in Table 1, VELCRO can achieve 13.5–30% energy consumption savings while maintaining the same accuracy of the uncompressed model.

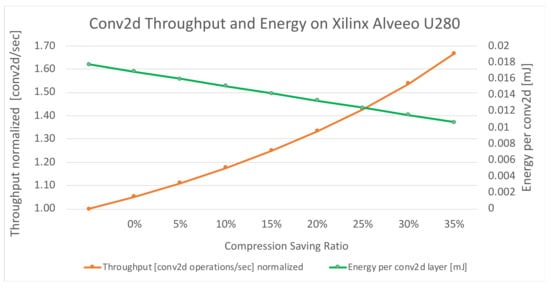
Figure 4. VELCRO throughput and energy consumption Xilinx^® AlveoTM U280 Accelerator Card.

References

Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90.
He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016.
Bianco, S.; Cadene, R.; Celona, L.; Napoletano, P. Benchmark Analysis of Representative Deep Neural Network Architectures. IEEE Access 2018, 6, 64270–64277.
Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252.
Reed, R. Pruning algorithms—A survey. IEEE Trans. Neural Netw. 1993, 4, 740–747.
LeCun, Y.; Denker, J.S.; Solla, S.; Howard, R.E.; Jackel, L.D. Optimal brain damage. In Advances in Neural Information Processing Systems (NIPS 1989); Touretzky, D., Ed.; Morgan Kaufmann: Denver, CO, USA, 1990; Volume 2.
Hassibi, B.; Stork, D.G.; Wolff, G.J. Optimal Brain Surgeon and general network pruning. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 28 March–1 April 1993; Volume 1, pp. 293–299.
Zhang, C.; Bengio, S.; Hardt, M.; Recht, B.; Vinyals, O. Understanding Deep Learning Requires Rethinking Generalization. arXiv 2016, arXiv:1611.03530.
Vanhoucke, V.; Senior, A.; Mao, M.Z. Improving the speed of neural networks on CPUs. In Deep Learning and Unsupervised Feature Learning Workshop; NIPS: Granada, Spain, 2011.
Gong, Y.; Liu, L.; Yang, M.; Bourdev, L. Compressing deep convolutional networks using vector quantization. arXiv 2014, arXiv:1412.6115.
Courbariaux, M.; Bengio, Y.; David, J.-P. BinaryConnect: Training Deep Neural Networks with binary weights during propagations. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Bali, Indonesia, 8–12 December 2015.
Lin, Z.; Courbariaux, M.; Memisevic, R.; Bengio, Y. Neural networks with few multiplications. arXiv 2015, arXiv:1510.03009.
Wang, Y.; Zhang, X.; Xie, L.; Zhou, J.; Su, H.; Zhang, B.; Hu, X. Pruning from Scratch. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 12273–12280.
Molchanov, P.; Tyree, S.; Karras, T.; Aila, T.; Kautz, J. Pruning Convolutional Neural Networks for Resource Efficient Inference. arXiv 2016, arXiv:1611.06440.
Luo, J.-H.; Wu, J. Neural Network Pruning with Residual-Connections and Limited-Data. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020.
Han, S.; Mao, H.; Dally, W.J. Deep compression: Compressing deep neural networks with pruning, trained quantization and Huffman coding. arXiv 2015, arXiv:1510.00149.
Han, S.; Pool, J.; Tran, J.; Dally, W.J. Learning both weights and connections for efficient neural networks. arXiv 2015, arXiv:1506.02626.
Boone-Sifuentes, T.; Robles-Kelly, A.; Nazari, A. Max-Variance Convolutional Neural Network Model Compression. In Proceedings of the 2020 Digital Image Computing: Techniques and Applications (DICTA), Melbourne, Australia, 29 November–2 December 2020; pp. 1–6.
Xilinx. Breathe New Life into Your Data Center with Alveo Adaptable Accelerator Cards. Xilinx White Paper, WP499 (v1.0). Available online: https://www.xilinx.com/support/documentation/white_papers/wp499-alveo-intro.pdf (accessed on 19 November 2018).

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.

Upload a video for this entry

Information

Subjects: Computer Science, Artificial Intelligence

Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :

Freddy Gabbay

View Times: 766

Update Date: 08 Nov 2021

Table of Contents

Video Upload Options

Confirm